Dinamik Sistemler ve Kaos 2012 Erciyes niversitesi Mhendislik

Dinamik Sistemler ve Kaos 2012 Erciyes Üniversitesi Mühendislik Fakültesi Elektrik-Elektronik Mühendisliği Bölümü Enis GÜNAY egunay@erciyes. edu. tr em. erciyes. edu. tr/egunay

Dersin Organizasyonu • Materyal • Ders I ▫ ▫ ▫ Dinamik sistemlerin gelişimi Başlangıç Durumuna Hassas Bağlılık Doğanın Geometrisi: Fraktallar Kaos ve Diğer Bilimler Dinamiğe Bir Bakış Dinamiğin Çeşitleri

Materyal • Dersin Kodu: EEM 515 • Web Sitesi: em. erciyes. edu. tr/egunay • Kitap: ▫ “Nonlinear Dynamics and Chaos: with applications to Physics, Biology, Chemistry and Engineering” Steven H. Strogatz. • Ders Günü ve Saatleri: ▫ Her Cuma saat 16 -18 arası.

Dinamik Sistemlerin Gelişimi • “Doğanın bir basitliği ve bundan dolay büyük bir güzelliği vardır. ” R. Feynmann • Gökyüzünde hareket eden bulutlar, içilen bir sigaradan havaya yükselen duman, bir musluktan akan su damlalar, rüzgârın etkisiyle oradan buraya salınan yapraklar. . . • Bütün bunlar ve yaşamımız boyunca her an tanık olduğumuz birçok olay bize düzensiz, kural dışı, devamsız olarak niteleyebileceğimiz oluşumlar olarak gözükür.

Dinamik Sistemlerin Gelişimi ▫ Isaac Newton: (d. 4 Ocak 1643 – ö. 31 Mart 1727) • 1687’de yayınlanan kitabı Philosophiæ Naturalis Principia Mathematica, klasik mekaniğin temelini yaratmıştır ve tarihte en önemli bilimsel kitaplardan biridir. • Bu çalışmasında Newton evrensel kütle çekimini ve hareketin üç kanununu ortaya koymuş ve sonraki üç yüzyıl boyunca bu bakış açısı bilim dünyasına egemen olmuştur. • Newton dünyadaki nesnelerin hareketleri ile gökyüzündeki nesnelerin aynı doğal yasalar ile yönetildiklerini kendi kütle çekim kanunu ile Kepler’in gezegen hareketleri kanunu arasındaki tutarlılıklar ile göstermiştir.

Dinamik Sistemlerin Gelişimi • Newton o zamana kadar çözülemeyen iki boyutlu problemi çözmüş, yani dünyanın güneş etrafındaki hareketini, birbirlerine uyguladıkları yerçekiminin ters-kare kanununu tanımlamıştı. • Newton’u takip eden matematikçiler ve fizikçiler, Newton’un analitik metodunu üç boyutlu probleme yani güneş, dünya ve aydan oluşan sisteme uygunlaştırmaya çalışmışlardır. Ancak mevcut metotların bu problemi çözmek için yeterli olmadığı görülmüştür.

Dinamik Sistemlerin Gelişimi ▫ Jules Henri Poincaré 29 Nisan 1854 Nans'de doğdu, 17 Temmuz 1912 Paris'te öldü. Fransız matematikçi ve fizikçi. • 1800’lerin sonlarına doğru Poincaré, bu tür problemlerin çözümleri için geometrik yaklaşımlar geliştirmiştir. • Poincaré başlangıç şartlarına duyarlı, periyodik olmayan davranışlar gösteren kararlı sistemlerde kaosun var olabileceğini tanımlayan böylece sistem üzerine uzun süreli tahminlerin yapılamayacağını belirten ilk kişidir.

Dinamik Sistemlerin Gelişimi • Bulunduğumuz yüzyılın birinci yarısı içinde, H. Poincare’in ilk yaklaşımından sonra kaosun açıkça bilim camiasında etkinliğini göstermediğini söyleyebiliriz. • Doğrusal olmayan osilasyonlar büyük ölçüde radyo, radar ve lazer teknolojisinde hayati gelişmeler sağladı. Teorik yapıda ise osilasyonlar yeni matematiksel teknikler keşfedilmesine neden oldular. • Bu alanda özellikle Van der Pol, Andronov, Littlewood, Cartwright, Levinson ve Smale in çalışmaları dikkate değerdir. Bununla beraber, ayrı bir gelişme olarak Birkhoff ve sonra Kolmogorof, Moser’in yardımıyla Poincare in geometrik metodlar klasik mekaniğe de yer verilerek geliştirildi.

Dinamik Sistemlerin Gelişimi • 1950’li yıllarda yüksek hızlı bilgisayarların keşfi dinamik için bir dönüm noktası oldu. Bilgisayarlar yardımıyla denklemlerin o zamana kadar mümkün olmayan incelemeleri yapıldı. • Bu türden doğrusal olmayan uygulamalar, Lorenz in 1963 de keşfettiği garip çekicilere kadar sürdü. Lorenz hava durumunun niçin tahmin edilemeyen yapıya sahip olduğunu anlamak için bir konveksiyon rulolar modeli geliştiriyordu. • Çözüm için makineye verdiği sayılar çok küçük değişikliklerle işleme konulduğunda çok farklı sonuçlar elde etti. • İlk garip çekiciyi bularak, üç boyutlu çizimle kaosun görülür bir yapısının olduğunu gösterdi.

Dinamik Sistemlerin Gelişimi • 1970’ler kaosun parlak yılları oldu. 1971 de D. Ruelle ve F. Takens, akışkanlardaki türbülansın başlangıcı konusunda yeni bir teori öne sürdü. • Bu teori, ayrıca garip çekiciler konusunda düşünceleri de içeriyordu. Birkaç yıl sonra, May yineleme haritalarında (iterated mapping) kaosun ilk örneklerini sergiledi. May’in yaptığı önemli katkılardan biri de kaosun pedagojisi üzerine verdiği çalışmalardır. • Feigenbaum ise kesin ve evrensel tanımlar ortaya koyarak düzenden kaosa geçişin doğasını inceledi. Bu yolla birçok farklı sistemin kaotik olabileceğini ortaya koydu. • Son çalışmalardan sayılabilecek bulgular da Gollup, Libchaber, Swinney, Linsay, Moon ve Westervelt gibi deneycilerden geldi. • Bu kişiler gerek akışkanlardaki gerekse yarı iletkenlerdeki, elektronik devrelerdeki ve kimyasal reaksiyonlardaki kaosun yapısını incelediler ve test ettiler. • Son zamanlarda yapılan dikkate değer bir kısım çalışmalarda Mandelbrot ve Winfree den geldi. • Mandelbrot, yeni bir geometrik anlayış oluşturdu ve grafikleri bilgisayar ortamında elde etmeyi başardı. • Winfree ise matematiksel biyolojinin ortaya çıkmasıyla biyolojik ritimleri, özellikle kalp atışlarını inceledi. Günümüzde hala pek çok araştırma yapılmasına rağmen kaos teorisinin oluşturulması daha çok zaman alacak gibidir.

Başlangıç Durumuna Hassas Bağlılık • II. Dünya Sava sonunda, MIT (Massachusetts Teknoloji Enstitüsü)´de hava tahminleri üzerine bilgisayar destekli araştırmalarda bulunan E. Lorenz, 1960´ta icad ettiği minyatür meteoroloji modeliyle meslektaşlar şaşırtmıştı. • Lorenz, ilkel bilgisayarını kullanarak havayı en basit şekilde ifade edilebilen bir hale indirgemişti. • Bilgisayar, havadaki ısı-basınç ilişkilerini, rüzgârın yönünü, siklon gruplamalarını sayısal olarak, her gün 12 denklem yardımıyla kaydediyordu. • Rüzgâr ve hava sıcaklıkları, Lorenz´in yazıcısından satır dökülürken dünyadaki gerçekleşme biçimiyle aynı davranışları gösteriyordu. Dahası, bu listelenen değerlerden hareketle tahminlerde de bulunabiliyordu.

Başlangıç Durumuna Hassas Bağlılık • Biraz uğraşıdan sonra sayıları, grafiğe de dökmeyi başardı. 1961´in kış aylarında bu işi kestirme yoldan yapmak için, makineye önceki rapor değerlerini klavyeden girdi. • Ancak rapordaki değerlerin sıfırdan sonraki üç rakamı yuvarlayarak, şaşkınlıkla gördü ki; hava durumu bir önceki dökümde yer alan şekilden umulmadık derecede sapmıştı. Bir süre sonra da; ilk dökümle hiç alakasız bir hava raporu grafiği elde etti.

Başlangıç Durumuna Hassas Bağlılık • Bu olay, Lorenz´e en küçük detayların bile ileride çok büyük sonuçlara neden olabileceğini ve hiçbir zaman uzun süreli bir hava tahmininin yapılamayacağını göstermişti. • Sistem ilk çıkış noktasıyla çok hassas olarak ilişkiliydi. • Bu olay J. H. Poincare, öyle ifade etmişti: Başlangıç şartlarındaki küçücük bir hata son olguda muazzam bir hataya neden olacaktır. Bu durumda, olacağı öngörmek olanaklı değildir. • Gerçekten de dünyanın en iyi hava tahminleri bile iki, üç günden öteye gitmiyor, bu süre aşıldığında spekülasyona dönüşüyor.

Başlangıç Durumuna Hassas Bağlılık • İlk defa Lorenz´in fark ettiği bu olguya kelebek etkisi denildi. • Buna göre; Florida kıyılarındaki bir kasırganın nedeni pekâlâ Pekin´de kanat çarpan bir kelebek olabilirdi. • Bu duruma örnek olarak bir bilardo masasında belli şekilde yerleşmiş toplarla oluşan sistem de verilebilir. • Burada, siyah topa başlangıçta verilecek en küçük hatalar bile ileride bütün topların yerleşimini değiştirebilir, beklenilmez durumlara neden olabilir. • Bu da, siyah topun hareketinin, başlangıç durumuna çok hassas bağlı olduğunu gösterir.

Doğanın Geometrisi: Fraktallar • B. Mandelbrot, IBM´de çalışırken; mühendislerin bilgisayardan bilgisayara bilgi aktarımında telefon hatlarındaki parazitlerden yakındıklarını duymuştu. • Parazitlerin periyodik olarak tekrarlanmasına rağmen, mühendisler bu durumu, karmaşık olduğundan yok edememişlerdi. • Mandelbrot, hatalı periyodu çok küçük zaman dilimlerine bölerek, hataların belirgin hale getirilebileceğini ve parazitlerin etkilerinin azaltılabileceğini düşünmüştü. • Bu düşünceye göre hata, ne kadar kısa sürerse sürsün, iletimin tamamen hatasız olduğu periyotlar daima olacaktır

Doğanın Geometrisi: Fraktallar • Bu, Cantor dizisi olarak bilinen soyut olguyla aynıydı: Bir doğruyu her defasında üçe bölerek ortadaki üçte birlik bölümü kaldırırsınız. • Kalan iki doğru parçasının her biri için de bunu tekrarlarsınız, böylece sonsuza değin devam edersiniz. • Geriye, sonsuz sayıda çok, fakat sonsuz dağınıklıkta bir toz grubu kalır.

Doğanın Geometrisi: Fraktallar • Mandelbrot, yaşadığımız evrende yuvarlaklık, düzgünlük gibi unsurların, düzgün geometrik şekillerin olmadığını; esasında pütürlü, pürüzlü, girintili, çıkıntılı, kırık geometrik yapılarla evrenin oluştuğunu düşünüyordu. • Hiçbir da konik olmadığı gibi, şimşek de bir doğru boyunca yol almıyordu. • Onun tezine göre, aslında bir sahil, bir bakıma sonsuz uzunluktaydı. • Bu, aslında elinizde bulunan ölçü aletine bağlıydı.

Doğanın Geometrisi: Fraktallar • Şöyle ki; bir pergeli harita üstünde iki ucu arası 2 cm açıklık olacak şekilde açalım ve Ege sahili boyunca pergeli yürütelim. • Gerçek uzunluk için yaklaşık bir değer bulmuş oluruz. Çünkü pergelimiz girinti ve çıkıntıları atlayacaktır. • Sonra, pergelin açıklığını 1 cm yapalım. Bu ölçümle de daha fazla uzunluk bulmuş oluruz. Çünkü pergelimiz daha çok ayrıntıyı yakalayacaktır. • Bu işlemi, 5 mm için tekrarlarsak göreceğiz ki bu açıklıklar küçülttükçe sonucumuz farklı olacaktır. Hatta kıyıdaki bir salyangozun ölçüm sonucu, bu iki gözlemcininkinden daha fazla olacaktır.

Doğanın Geometrisi: Fraktallar • Öklit tarz ölçümlerin, düzensiz şekillerin özünü ölçmede yetersiz kalması Mandelbrot´u, yeni geometri ilkesini ortaya atması için zorluyordu. • Hatta bu yeni geometrik anlayışa oğlunun latince sözlüğü yardımıyla bir isim de buldu: Fraktal. • Fraktal, aklın gözüne göre sonsuzu görebilmenin bir yoludur. Bu terimin bir özelliği de kendine benzerlik anlamını taşıyor olmasıydı.

Doğanın Geometrisi: Fraktallar • 1904´te İsveçli matematikçi Koch´un tanımladığı eğri, Mandelbrot´un yeni geometrisine bir örnek olarak verilebilir: Bir eş kenar üçgenin her kenarının ortasındaki üçte birlik kısmı alın. • Bunlarla yeni bir üçgen oluşturun. Yeni üçgen şekil olarak aynı ve büyüklük olarak ilkinin üçte biri kadardır. • Böylece devam edildiğinde ideal bir kar tanesi elde edersiniz. İncelendiğinde sürekli, kendini kesmeyen, toplam alanın sınırlı olduğu fakat uzunluğunun sonsuz olduğu bir eğridir. • Çevresine bir daire çizildiğinde bu şekil asla daire dışına taşınmaz.

Doğanın Geometrisi: Fraktallar • Daha sonra birçok matematikçi bunun gibi çeşitli eğriler düşündüler: ▫ Peano eğrileri, Sierpinski halılar, Menger süngeri. . . • Fraktalların en önemli özelliği, düşünüldüklerinde doğayla ideal benzerlikte şekiller vermeleridir. • Bir anlamda, doğanın geometri anlayışını yansıtıyordu. • Yer kabuğunun şekli ve yapısı üzerine ihtisas yaparken çalışmasına fraktallar inceleyerek başlayan C. Scholz bu konuda unlar söyler: ▫ Bu, yeryüzünün değişen boyutlar n bütün kapsamıyla ele almamız mümkün kılan tek modeldir.

Doğanın Geometrisi: Fraktallar

Kaos ve Diğer Bilimler • Kaos, bir durumun değil, bir sürecin ve oluşumun bilimidir. • Doğanın da her zaman aksiyon dolu ve evrimle iç içe olduğu düşünüldüğünde, sanki doğanın dilidir, kaos. • Bu yüzden, her bilim dalında yadsınamaz bir öneme sahiptir. • Ekonomiden astronomiye, tıptan ekolojiye kadar pek çok alanda insanların faydasına sunulan çalışmalar yapılmaktadır.

Dinamiğe Bir Bakış • Dinamik, genel anlamda bir sistemin zaman içinde geçirdiği değişimlerin incelendiği ve ifade edildiği fizik dalı olarak tanımlanır. • Günümüzde dinamik birbirinden gittikçe ayrılan, çeşitlenen bilim dallarının aksine birçok bilim dalını bir araya getiren bir disiplin görünümündedir. • Dinamiğin kurucusu olarak Newton kabul edilir. 17. yüzyılın ortalarında Newton; diferansiyel denklemlerin ilk örneklerini ortaya atmış buna dayalı olarak cisimlerin hareket kanunlarını tespit etmiştir.

Dinamiğe Bir Bakış • Özellikle gök cisimlerinin hareketlerini açıklayan evrensel çekim yasası evreni tanımamız yolunda vazgeçilmez öneme sahiptir. • Daha sonralar J. Kepler, Batlamyus (Ptolomeos)’dan beri yapılan gözlemlerden yararlanarak uzaydaki cisimlerin dinamiğini net olarak açıklamıştır. • G. Galilei’nin yaptığı ufak çaptaki incelemeler dışında yukarıdaki çalışmalar dinamiğin ilk göz ağrısıdır.

Dinamiğe Bir Bakış • Newton, güneşin çevresinde dönen dünyanın hareketinin hesaplanması problemini (iki cisim problemi) ele alıp gravitasyonel çekim kuvvetinin bir ters kare kuvvet olduğunu belirtmişti. • Buna göre G, evrensel çekim sabiti, M ve M’ etkileşen cisimlerin kütleleri ve R, bu cisimler arasındaki uzaklık olmak üzere kuvvet şu şekilde ifade edilir: F = - GMM’ / R 2

Dinamiğe Bir Bakış • Sonraki kuşaklar ise daha ilginç bir problem olan üç cisim problemini ele almaya çalıştılar. • Örneğin Güneş, Dünya ve Ay üçlüsü için gerekli hesaplar analitik çalışmaların özünü oluşturur. Ama bu problemin çözümü sanıldığı kadar kolay değildi. • Sanki Newton ardında yeni bir metot bırakmış ve sonra ardından gelenlere biraz da siz uğraşın demişti. • Ancak yıllarca süren uğraş, Newton’un yolundan giderek sorunu halletmenin imkânsız olduğunu bilimcilere gösterdi.

Dinamiğe Bir Bakış • 1982 yılında; H. Poincare, çözüm için farklı bir yol düşündü. • Ona göre Newton’un ortaya koyduğu kesin çözümler ancak doğanın sınırlı ve marjinal durumlarında geçerli olabilirdi. • Etkileşmeler çoğaldığında hesaplamalar da iflas etmeliydi. • Poincaré üç cisim probleminin üstesinden gelmek için ilginç bir taktik kullandı. • Hareketi izlenecek olan gezegenin bütün zamanlardaki kesin pozisyonların incelemek yerine şunu soruyordu: ▫ Güneş sistemi daima böyle durağan mı kalacaktır, yoksa birkaç gezegen sonradan, sonsuzluğa doğru kaçar mı?

• Poincaré “Bilim ve Yöntem” adlı kitabında şöyle yazar: ▫ “Dikkatimizden kaçan küçücük noktalardan biri öylesine büyük bir sonuca neden olur ki, biz de kalkıp bu sonucun rastlantı neticesinde ortaya çıktığını söyleriz. ▫ Doğanın yasalarını ve evrenin başlangıç anındaki durumunu tam olarak bilebilseydik, evrenin başlangıç durumunu izleyen daha sonraki anlardan birinde hangi durumda olacağını da tam olarak öngörmemiz mümkün olabilirdi. ▫ Bu sayede, başlangıç durumunu izleyen durumu aynı şekilde yaklaşık değerler olarak öngörmemiz olanaklı olsa bütün istediğimiz gerçekleşmiş olur ve biz de bu fenomenin öngörülmüş olduğunu, yasalara uygun olarak cereyan ettiğini söyleriz. ” • Poincaré in bu düşünceleri başlı başına bir dal olan dinamiği etkileyerek onun birtakım ayrılmalara uğrayacağının ilk sinyallerini veriyordu.

Dinamiğin Çeşitleri • Dinamik sistemlerin iki ana çeşidi mevcuttur. Bunlar: ▫ diferansiyel denklemler ▫ yineleme haritalar (fark denklemleri-iterated maps). • Diferansiyel denklemler bir fiziksel sistemin zaman içindeki evrimini tanımlar. • Oysa yineleme haritalar zamana bağlı olmayan problemlerde kullanılmaktadır. • İncelenen bir olaydaki diferansiyel denklemin özelliği o olayın doğrusal olup olmadığını belirtir.

Dinamiğin Çeşitleri • Söz gelimi; sönümlü harmonik osilatörü ele alalım. • Bu tip bir hareket birim kütle (unit mass) problemlerinde, akışkan sürüklenme kuvvetinde (viscous drag force) yada bir LCR devresinde görülebilir.

Dinamiğin Çeşitleri • Burada x(t) sistemin osilasyon genliğini ifade ederken k/2 pi sistemin doğal frekansını göstermektedir. • b sönüm faktörünü belirlemektedir. • Burada b sıfır olarak alındığında x(0)=A, dx(0)/dt=0 başlangıç koşulları için sistem basit harmonik vibrasyonlar gösterecektir:

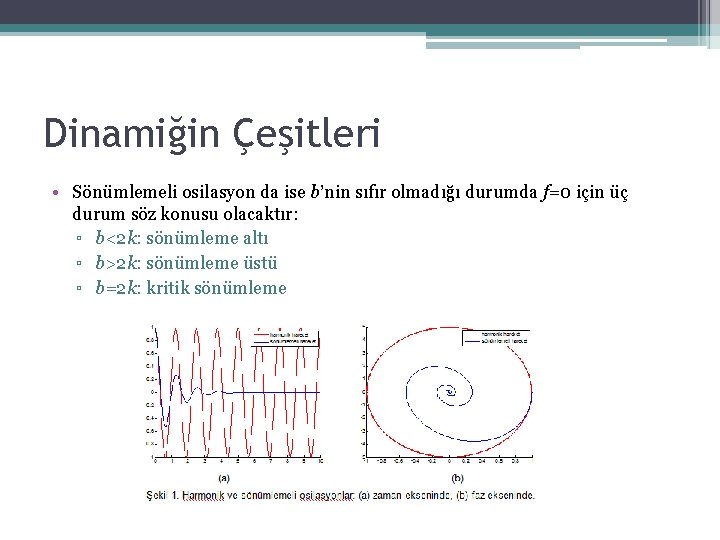
Dinamiğin Çeşitleri • Sönümlemeli osilasyon da ise b’nin sıfır olmadığı durumda f=0 için üç durum söz konusu olacaktır: ▫ b<2 k: sönümleme altı ▫ b>2 k: sönümleme üstü ▫ b=2 k: kritik sönümleme

Dinamiğin Çeşitleri

Dinamiğin Çeşitleri

Dinamik Sistemler ve Kaos • Bir sürecin lineer olup olmaması, bu manada, sistemi betimleyen dinamik denklemlere bağlıydı. • Bu durumda, pekâlâ bir sistemin denklemlerine bakılarak hareketinin yapısı hakkında bilgi edinilebilir. • Fakat doğrusal olmayan bir davranışın kaotik olup olmadığının belirlenmesi nasıl yapılır? • Her kaotik hareket bir doğrusal olmayan davranış sınıfına dâhil edilebileceği gibi her doğrusal olmayan davranış kaotik yapı içermez. • Gerçekte bu ayrımın yapılması çok zor olup, bilimsel alanda bu iş için kullanılan değişik metotlar mevcuttur.

Dinamik Sistemler ve Kaos

Dinamik Sistemler ve Kaos