atallanmalar Bifurcations Erciyes niversitesi Mhendislik Fakltesi ElektrikElektronik Mhendislii
Çatallanmalar (Bifurcations) Erciyes Üniversitesi Mühendislik Fakültesi Elektrik-Elektronik Mühendisliği Bölümü Enis GÜNAY egunay@erciyes. edu. tr em. erciyes. edu. tr/egunay

Bifurcations • Bir önceki bölümde görmüş olduğumuz tek boyutlu sistemlerin akışı sistem parametrelerindeki oluşabilecek değişiklere duyarlıdır. • Buna göre sistem parametrelerindeki değişimler ile sistemin sabit noktaları oluşturulup yok edilebilir ya da kararlılık durumları değişkenlikler gösterebilir. • Dinamik sistemlerde sistemi oluşturan parametrelere bağımlı bu tür yapısal değişikliklere çatallanma (bifurcation) adı verilir. • Bu bölümde öncelikle sabit noktalarda görülen çatallanmalar incelenecektir.

Saddle-Node (Eğer-Düğüm) Çatallanması • Saddle-Node dallanmaları sabit noktaların önce oluşturulup sonra da yok edildiği dallanma çeşitleridir. • Parametrik değişim sonucu iki sabit nokta birbirlerine doğru hareketlenip çarpışırlar ve birbirlerini yok ederler.

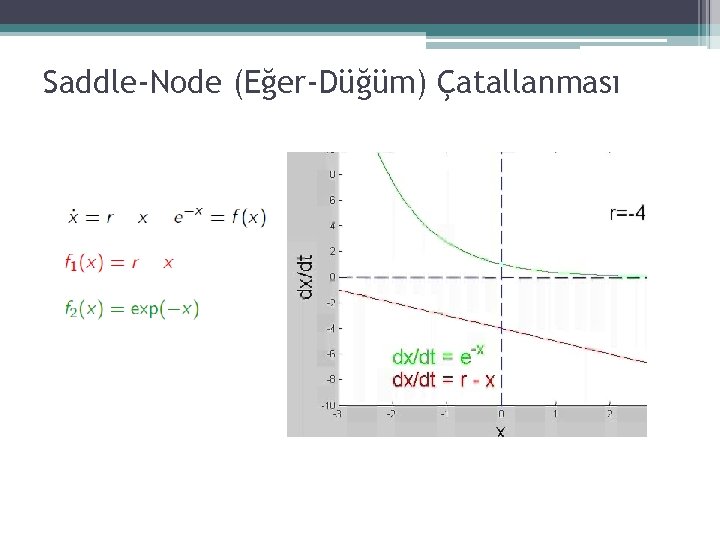
Saddle-Node (Eğer-Düğüm) Çatallanması • Aşağıdaki gibi birinci dereceden bir sistemde r parametresinin pozitif, negatif ya da sıfır olması sistemin kararlılık noktaları üzerindeki etkisi şekildeki gibi olacaktır.

Saddle-Node (Eğer-Düğüm) Çatallanması

Saddle-Node (Eğer-Düğüm) Çatallanması

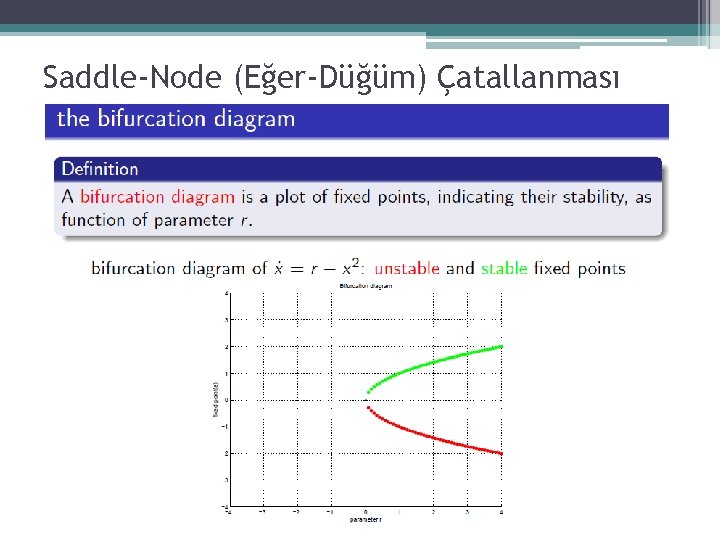
Saddle-Node (Eğer-Düğüm) Çatallanması r parametresi negatif değerlerden sıfır değerine doğru yaklaştıkça iki sabit noktanın birbirlerine doğru hareketlendiği, r=0 için yarı-kararlı bir sabit noktanın elde edildiği, r>0 için ise sistemde artık sabit bir noktanın oluşmadığı görülmektedir.

Saddle-Node (Eğer-Düğüm) Çatallanması
Saddle-Node (Eğer-Düğüm) Çatallanması
Saddle-Node (Eğer-Düğüm) Çatallanması

Saddle-Node (Eğer-Düğüm) Çatallanması

Saddle-Node (Eğer-Düğüm) Çatallanması noktasında saddle-node çatallanmasına sahiptir.

Saddle-Node (Eğer-Düğüm) Çatallanmasının Analitik Olarak Tanımlanması Bir f(x, r)’nin (x*, r*)’deki çatallanması Taylor açılımı kullanılarak, saddle-node çatallanması aşağıdaki dört özellik kullanılarak tanımlanabilir: Buna göre (x*, r*) için saddle-node çatallanmasının genelleştirilmiş hali:

Saddle-Node (Eğer-Düğüm) Çatallanmasının Analitik Olarak Tanımlanması • Örnek olarak Böylece yukarıdaki iki fonksiyon da bifurkasyon değeri r*=1’e yaklaştıklarında aynı davranışı göstermeliler. Bunu gösterebilmek için her iki sistemin Taylor açılımına bakmak gerekecektir.

Taylor Açılımları

Taylor Açılımları

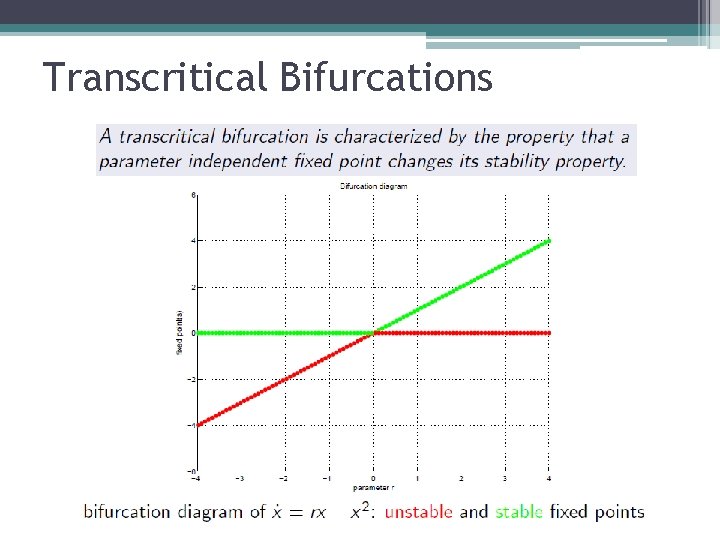
Transcritical Bifurcations

Transcritical Bifurcations
Transcritical Bifurcations

Pitchfork Bifurcations-supercritical case

Pitchfork Bifurcations-supercritical case
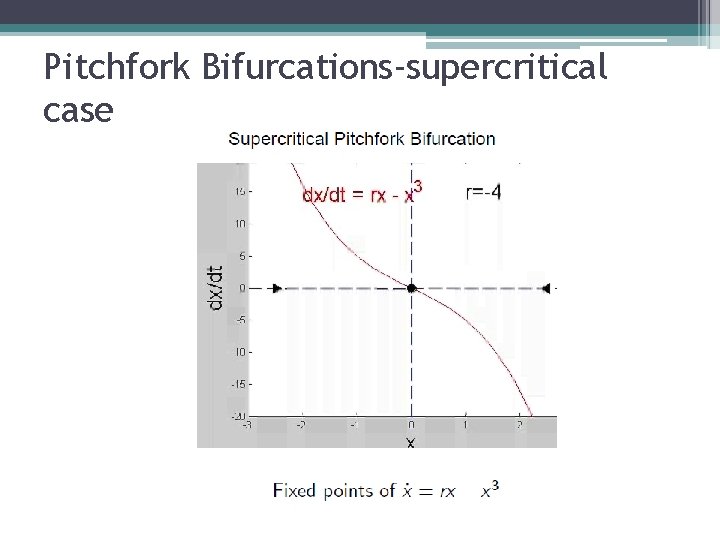
Pitchfork Bifurcations-supercritical case
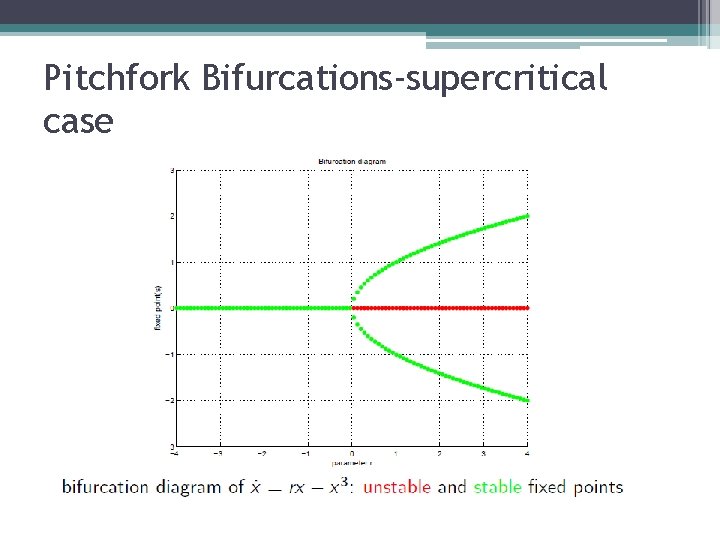
Pitchfork Bifurcations-supercritical case

Pitchfork Bifurcations-subcritical case

Pitchfork Bifurcations-subcritical case
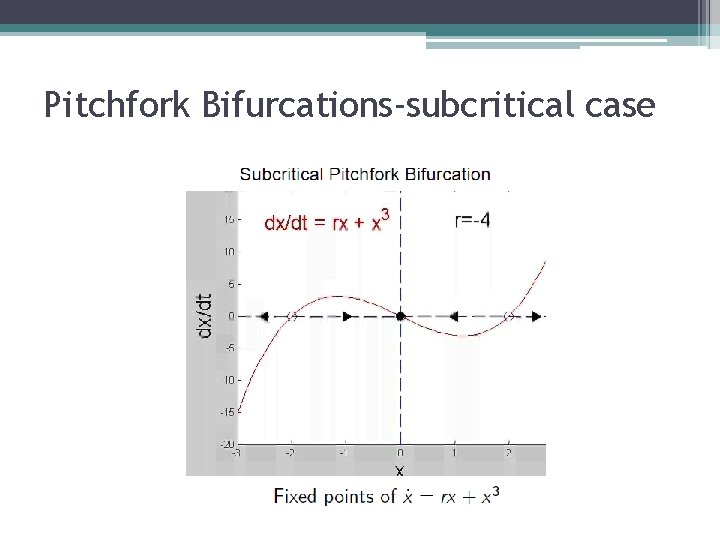
Pitchfork Bifurcations-subcritical case

Pitchfork Bifurcations-subcritical case
- Slides: 27