Giri Erciyes niversitesi Mhendislik Fakltesi ElektrikElektronik Mhendislii Blm

Giriş Erciyes Üniversitesi Mühendislik Fakültesi Elektrik-Elektronik Mühendisliği Bölümü Enis GÜNAY egunay@erciyes. edu. tr em. erciyes. edu. tr/egunay

Materyal • Dersin Kodu: EEM 530 • Web Sitesi: em. erciyes. edu. tr/egunay • Ders Günü ve Saatleri: ▫ Her Cuma saat 15. 30 -17. 00 arası.

MATLAB (Temeller-Symbolic Math Toolbox) • • clear 3^2*4 -3*2^5*(4 -2) sqrt(16) u=1: 2: 9 v=u. ^2 A=[1, 2; 3, 4] A' det(A) % Basit aritmetik. % Karekök alma. % Vektör gösterimi. % Üs alma. % 2 x 2 boyutlu matris. % Matrisin tersi. % Matrisin determinantı.

MATLAB (Temeller-Symbolic Math Toolbox) • B=[0, 3, 1; . 3, 0, 0; 0, . 5, 0] % 3 x 3 matris. • eig(B) % B’nin özdeğerleri. • [Vects, Vals]=eig(B) % B’nin özdeğerleri ve özvektörleri • C=[100; 200; 300] % 3 x 1 matris. • D=B*C % Matris çarpımı. • E=B^4 % Matrisin üssel değeri. • z 1=1+i % Karmaşık sayılar. • z 4=2*z 1 -z 2*z 3 % Karmaşık aritmetik.

MATLAB (Temeller-Symbolic Math Toolbox) • • • abs(z 1) % z 1’in mutlak değeri (genlik) real(z 1) % z 1’in gerçel kısmı. imag(z 1) % z 1’in imajiner kısmı. exp(i*z 1) % z 1’in eksponansiyeli. sym(1/2)+sym(3/4) % Sembolik aritmetik. 1/2+3/4 % Double precision. (64 bitlik floating point sayılara verilen isim. ) • vpa(pi, 50) % Değişken hassasiyet (Variable precision) • syms x y z % Sembolik objeler

MATLAB (Temeller-Symbolic Math Toolbox) • • • z=x^3 -y^3 factor(z) % faktörizasyon. expand(ans) % ekspansiyon. simplify(z/(x-y)) % basitleştirme. syms a b [a, b]=solve('tau*x*y', 'tau*x*y-y') % eş zamanlı denklem çözümü • f='mu*x*(1 -x)' % fonksiyon tanımlama. • subs(f, x, 1/2) % Evaluate f(1/2).

MATLAB (Temeller-Symbolic Math Toolbox) • • • fof=subs(f, x, f) % komozite fonksiyon. limit(x/sin(x), x, 0) % limit alma. diff(f, x) % türev alma. diff('x^2+3*x*y-2*y^2', 'y', 2) % kısmi türev alma int('sin(x)*cos(x)', x, 0, pi/2) % integral alma. int('1/x', x, 0, inf) % Improper integration.

MATLAB (Temeller-Symbolic Math Toolbox) • • syms n s w s 1=symsum(1/n^2, 1, inf) % sembolik toplama g=exp(x) taylor(g, 10) % Taylor serisine açılım. laplace(x^3) % Laplace transformu. ilaplace(1/(s-a)) % Ters laplace transformu. fourier(exp(-x^2)) % Fourier transform. ifourier(pi/(1+w^2)) % Ters fourier transformu.

MATLAB (Çizim-Diferansiyel Denklemler) • • clear % Basit foksiyon çizimi. x=-2: . 01: 2; plot(x, x. ^2)

MATLAB (Çizim-Diferansiyel Denklemler) • % İki fonksiyonun tek grafikte çizimi. • t=0: . 1: 100; • y 1=exp(. 1*t). *cos(t); y 2=cos(t); • plot(t, y 1, t, y 2), legend('y 1', 'y 2')

MATLAB (Çizim-Diferansiyel Denklemler) • % Sembolik çizim. • ezplot('x^2', [-2, 2]) • ezplot('exp(t)*sin(t)'), xlabel('time'), y label('current'), title('dec ay')

MATLAB (Çizim-Diferansiyel Denklemler) • % 50 x 50’lik bir grid ile 3 D çizim. • ezcontour('y^2/2 x^2/2+x^4/4', [-2, 2], 50) • ezsurfc('y^2/2 x^2/2+x^4/4', [-2, 2], 50)

MATLAB (Çizim-Diferansiyel Denklemler) • % Parametrik çizim. • ezplot('t^3 -4*t', 't^2', [-3, 3])

MATLAB (Çizim-Diferansiyel Denklemler) • % 3 -D parametrik çizim. • ezplot 3('sin(t)', 'cos(t)', 't', [-10, 10])

MATLAB (Çizim-Diferansiyel Denklemler) • % Symbolic solutions to o. d. e's. • dsolve('Dx=-x/t') ▫ C 2/t • dsolve('Dx=-x/t', 'x(0)=1') ▫ [ empty sym ] • dsolve('D 2 I+5*DI+6*I=10*sin(t)', 'I(0)=0', 'DI(0) =0') ▫ ? ? ? Error using ==> dsolve at 145 ▫ There are more ODEs than variables.

MATLAB (Çizim-Diferansiyel Denklemler) • % Linear systems of o. d. e's. • [x, y]=dsolve('Dx=3*x+4*y', 'Dy=-4*x+3*y') ▫ x =(C 6*i)/exp(t*(4*i - 3)) - C 5*i*exp(t*(4*i + 3)) ▫ y =C 5*exp(t*(4*i + 3)) + C 6/exp(t*(4*i - 3)) • [x, y]=dsolve('Dx=x^2', 'Dy=y^2', 'x(0)=1, y(0)=1') ▫ x =-1/(t – 1) ▫ y =-1/(t - 1)

MATLAB (Çizim-Diferansiyel Denklemler) • % A 3 -D linear system. • [x, y, z]=dsolve('Dx=x', 'Dy=y', 'Dz=-z') ▫ x =C 20*exp(t) ▫ y =C 21*exp(t) ▫ z =C 19/exp(t)

MATLAB (Çizim-Diferansiyel Denklemler) • % Numerical solutions to o. d. e's. • deq 1=inline('x(1)*(. 1. 01*x(1))', 't', 'x'); • [t, xa]=ode 45(deq 1, [0 100], 50); • plot(t, xa(: , 1))

MATLAB (Çizim-Diferansiyel Denklemler) • • % A 2 -D system. deq 2=inline('[. 1*x(1)+x(2); -x(1)+. 1*x(2)]', 't', 'x'); [t, xb]=ode 45(deq 2, [0 50], [. 01, 0]); plot(xb(: , 1), xb(: , 2))

MATLAB (Çizim-Diferansiyel Denklemler) • % A 3 -D system. • deq 3=inline('[x(3)-x(1); x(2); x(3)17*x(1)+16]', 't', 'x'); • [t, xc]=ode 45(deq 3, [0 20], [. 8, . 8]); • plot 3(xc(: , 1), xc(: , 2), xc(: , 3 ))

MATLAB (Çizim-Diferansiyel Denklemler) • % A stiff system. • deq 4=inline('[x(2); 1000*(1 -(x(1))^2)*x(2)x(1)]', 't', 'x'); • [t, xd]=ode 23 s(deq 4, [0 3000], [. 01, 0]); • plot(xd(: , 1), xd(: , 2))

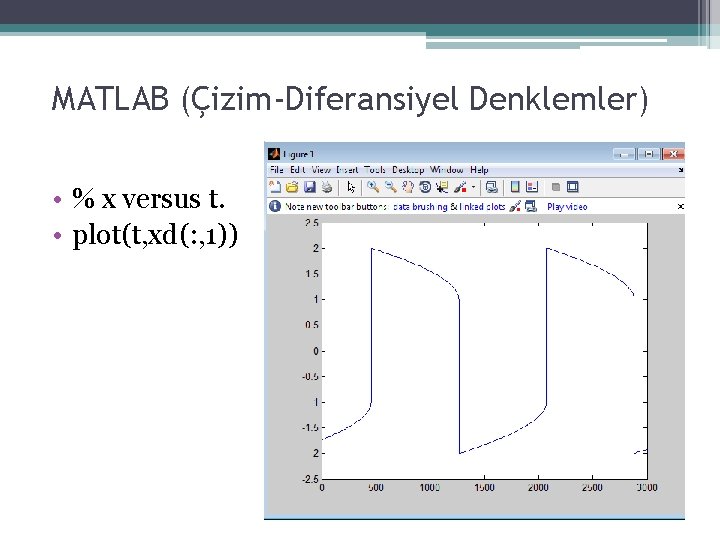
MATLAB (Çizim-Diferansiyel Denklemler) • % x versus t. • plot(t, xd(: , 1))