D WaitingLine Models Power Point presentation to accompany

D Waiting-Line Models Power. Point presentation to accompany Heizer and Render Operations Management, 10 e Principles of Operations Management, 8 e Power. Point slides by Jeff Heyl © 2011 Pearson Education, Inc. publishing as Prentice Hall D-1

Outline u Queuing Theory u Characteristics of a Waiting-Line System u Arrival Characteristics u Waiting-Line Characteristics u Service Characteristics u Measuring a Queue’s Performance u Queuing Costs © 2011 Pearson Education, Inc. publishing as Prentice Hall D-2

Outline – Continued u The Variety of Queuing Models u Model A(M/M/1): Single-Channel Queuing Model with Poisson Arrivals and Exponential Service Times u Model B(M/M/S): Multiple-Channel Queuing Model u Model C(M/D/1): Constant-Service-Time Model u Little’s Law u Model D: Limited-Population Model © 2011 Pearson Education, Inc. publishing as Prentice Hall D-3

Outline – Continued u Other Queuing Approaches © 2011 Pearson Education, Inc. publishing as Prentice Hall D-4

Learning Objectives When you complete this module you should be able to: 1. Describe the characteristics of arrivals, waiting lines, and service systems 2. Apply the single-channel queuing model equations 3. Conduct a cost analysis for a waiting line © 2011 Pearson Education, Inc. publishing as Prentice Hall D-5

Learning Objectives When you complete this module you should be able to: 4. Apply the multiple-channel queuing model formulas 5. Apply the constant-service-time model equations 6. Perform a limited-population model analysis © 2011 Pearson Education, Inc. publishing as Prentice Hall D-6

Queuing Theory u The study of waiting lines u Waiting lines are common situations u Useful in both manufacturing and service areas © 2011 Pearson Education, Inc. publishing as Prentice Hall D-7

Common Queuing Situations Situation Arrivals in Queue Service Process Supermarket Grocery shoppers Highway toll booth Automobiles Checkout clerks at cash register Collection of tolls at booth Doctor’s office Patients Computer system Programs to be run Telephone company Callers Bank Customer Switching equipment to forward calls Transactions handled by teller Machine maintenance Harbor Broken machines Repair people fix machines Ships and barges Dock workers load and unload © 2011 Pearson Education, Inc. publishing as Prentice Hall Treatment by doctors and nurses Computer processes jobs Table D. 1 D-8

Characteristics of Waiting. Line Systems 1. Arrivals or inputs to the system u Population size, behavior, statistical distribution 2. Queue discipline, or the waiting line itself u Limited or unlimited in length, discipline of people or items in it 3. The service facility u Design, statistical distribution of service times © 2011 Pearson Education, Inc. publishing as Prentice Hall D-9

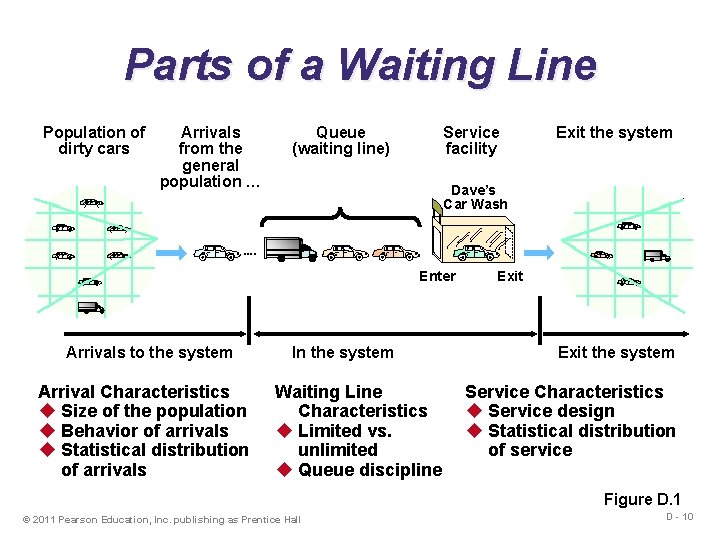
Parts of a Waiting Line Population of dirty cars Arrivals from the general population … Queue (waiting line) Service facility Dave’s Car Wash Enter Arrivals to the system Arrival Characteristics u Size of the population u Behavior of arrivals u Statistical distribution of arrivals Exit the system In the system Waiting Line Characteristics u Limited vs. unlimited u Queue discipline Exit the system Service Characteristics u Service design u Statistical distribution of service Figure D. 1 © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 10

Arrival Characteristics 1. Size of the population u Unlimited (infinite) or limited (finite) 2. Pattern of arrivals u Scheduled or random, often a Poisson distribution 3. Behavior of arrivals u Wait in the queue and do not switch lines u No balking or reneging © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 11

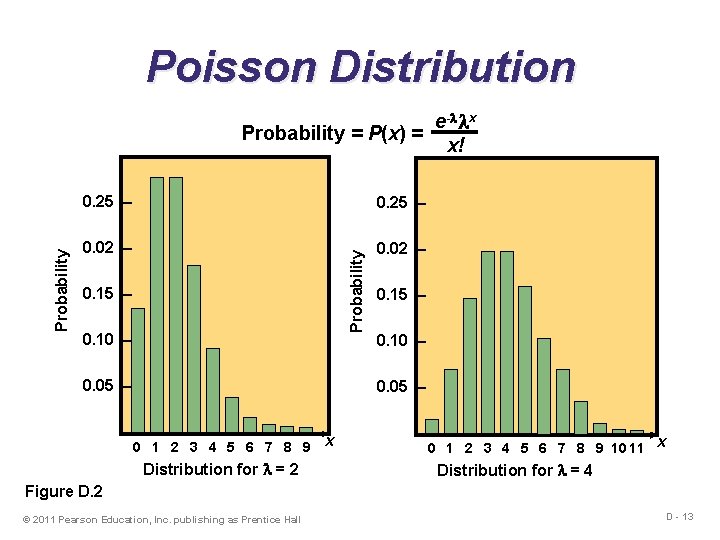
Poisson Distribution e- x P(x) = x! where P(x) x e = = for x = 0, 1, 2, 3, 4, … probability of x arrivals number of arrivals per unit of time average arrival rate 2. 7183 (which is the base of the natural logarithms) © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 12

Poisson Distribution 0. 25 – 0. 02 – Probability e- x Probability = P(x) = x! 0. 15 – 0. 10 – 0. 05 – – 0. 15 – 0. 10 – 0. 05 – 0 1 2 3 4 5 6 7 8 9 Distribution for = 2 x – 0 1 2 3 4 5 6 7 8 9 10 11 x Distribution for = 4 Figure D. 2 © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 13

Waiting-Line Characteristics u Limited or unlimited queue length u Queue discipline - first-in, first-out (FIFO) is most common u Other priority rules may be used in special circumstances © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 14

Service Characteristics u Queuing system designs u Single-channel system, multiplechannel system u Single-phase system, multiphase system u Service time distribution u Constant service time u Random service times, usually a negative exponential distribution © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 15

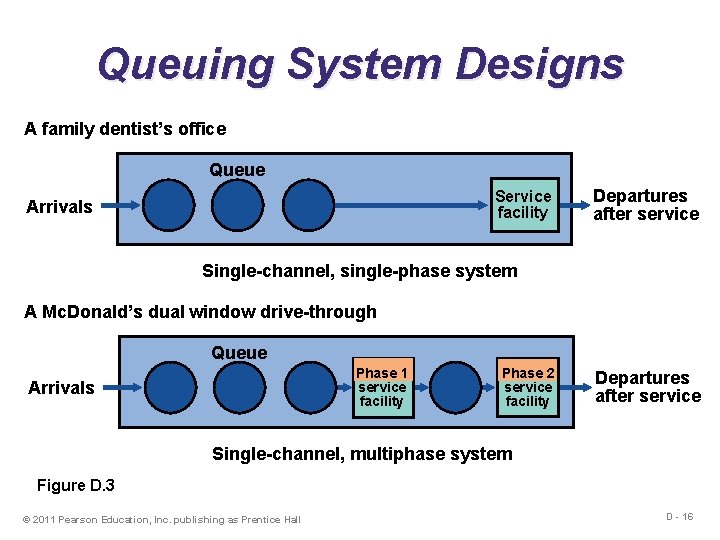
Queuing System Designs A family dentist’s office Queue Service facility Arrivals Departures after service Single-channel, single-phase system A Mc. Donald’s dual window drive-through Queue Phase 1 service facility Arrivals Phase 2 service facility Departures after service Single-channel, multiphase system Figure D. 3 © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 16

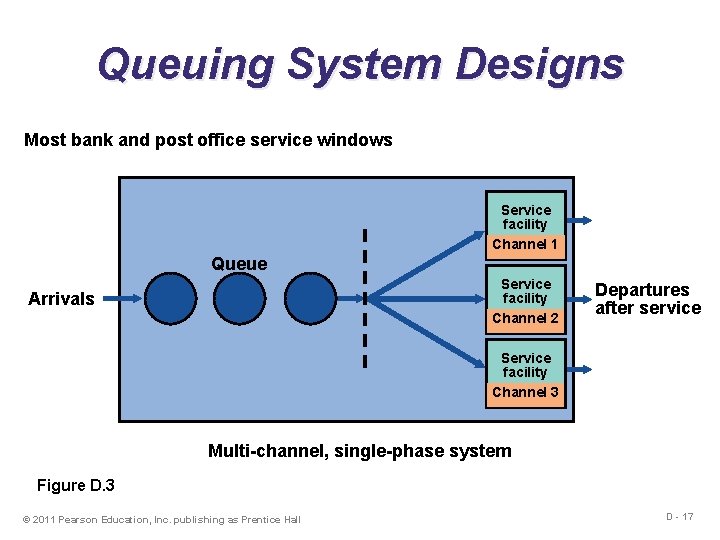
Queuing System Designs Most bank and post office service windows Service facility Channel 1 Queue Service facility Channel 2 Arrivals Departures after service Service facility Channel 3 Multi-channel, single-phase system Figure D. 3 © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 17

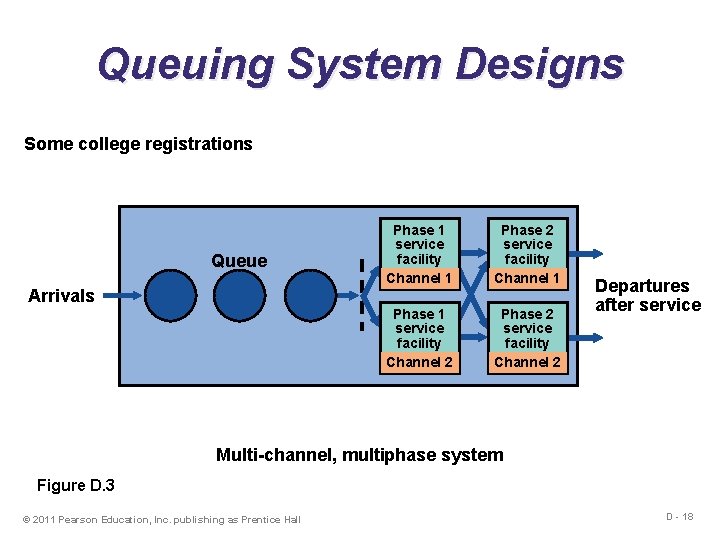
Queuing System Designs Some college registrations Queue Arrivals Phase 1 service facility Channel 1 Phase 2 service facility Channel 1 Phase 1 service facility Channel 2 Phase 2 service facility Channel 2 Departures after service Multi-channel, multiphase system Figure D. 3 © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 18

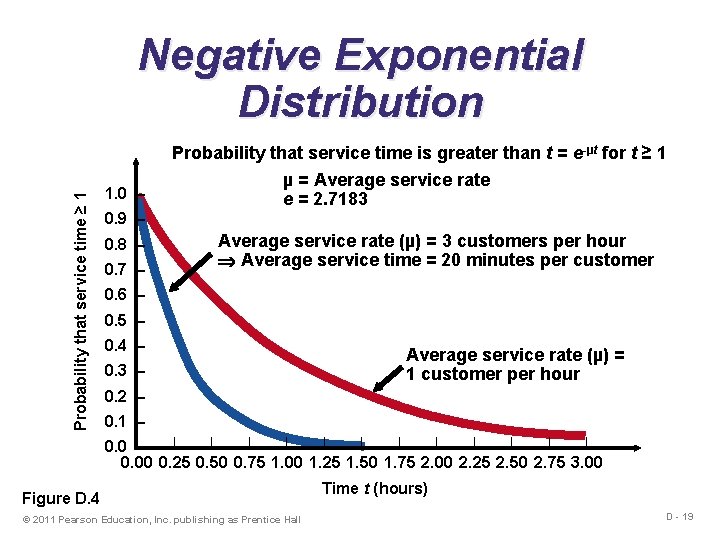
Probability that service time ≥ 1 Negative Exponential Distribution 1. 0 – Probability that service time is greater than t = e-µt for t ≥ 1 µ = Average service rate e = 2. 7183 0. 9 – 0. 8 – 0. 7 – Average service rate (µ) = 3 customers per hour Average service time = 20 minutes per customer 0. 6 – 0. 5 – 0. 4 – 0. 3 – Average service rate (µ) = 1 customer per hour 0. 2 – 0. 1 – | | | 0. 0 |– 0. 00 0. 25 0. 50 0. 75 1. 00 1. 25 1. 50 1. 75 2. 00 2. 25 2. 50 2. 75 3. 00 Figure D. 4 © 2011 Pearson Education, Inc. publishing as Prentice Hall Time t (hours) D - 19

Measuring Queue Performance 1. Average time that each customer or object spends in the queue 2. Average queue length 3. Average time each customer spends in the system 4. Average number of customers in the system 5. Probability that the service facility will be idle 6. Utilization factor for the system 7. Probability of a specific number of customers in the system © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 20

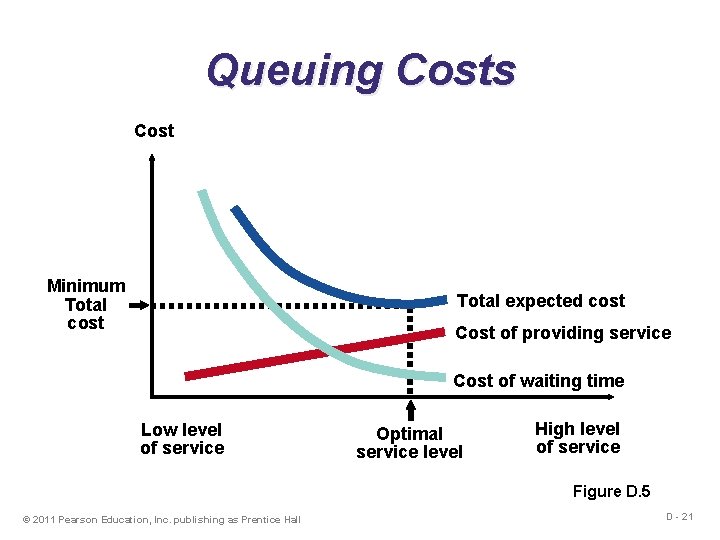
Queuing Costs Cost Minimum Total cost Total expected cost Cost of providing service Cost of waiting time Low level of service Optimal service level High level of service Figure D. 5 © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 21

Queuing Models The four queuing models here all assume: u Poisson distribution arrivals u FIFO discipline u A single-service phase © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 22

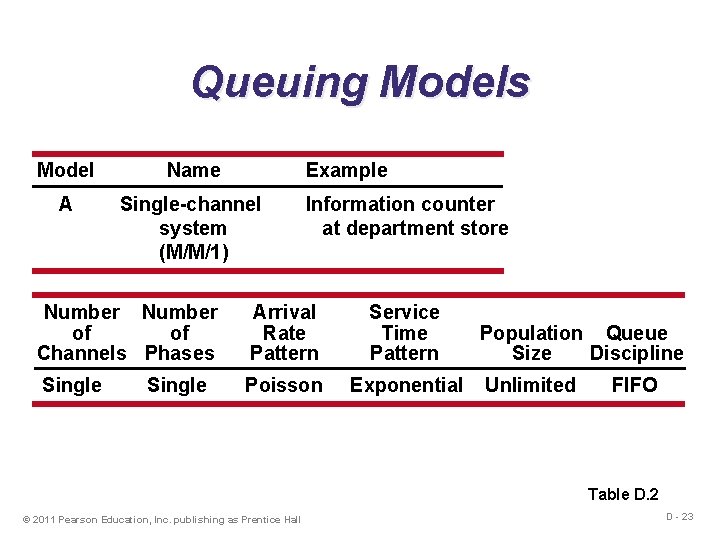
Queuing Models Model Name Example A Single-channel system (M/M/1) Information counter at department store Number of of Channels Phases Arrival Rate Pattern Service Time Pattern Single Poisson Exponential Single Population Queue Size Discipline Unlimited FIFO Table D. 2 © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 23

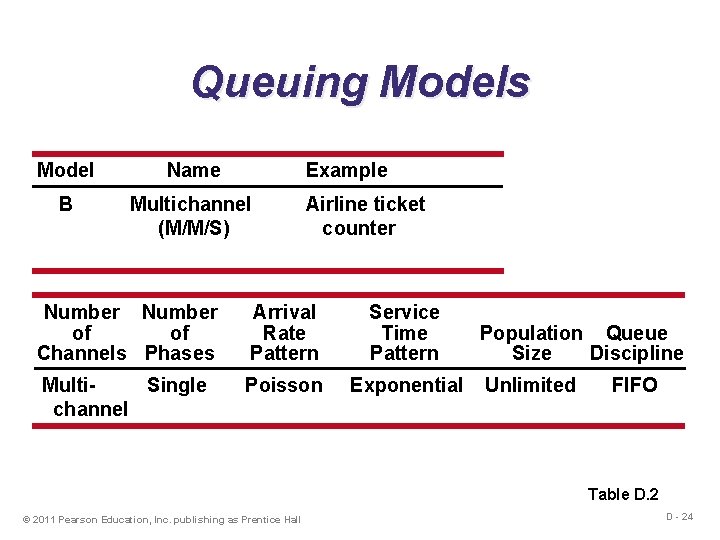
Queuing Models Model Name Example B Multichannel (M/M/S) Airline ticket counter Number of of Channels Phases Arrival Rate Pattern Service Time Pattern Multi. Single channel Poisson Exponential Population Queue Size Discipline Unlimited FIFO Table D. 2 © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 24

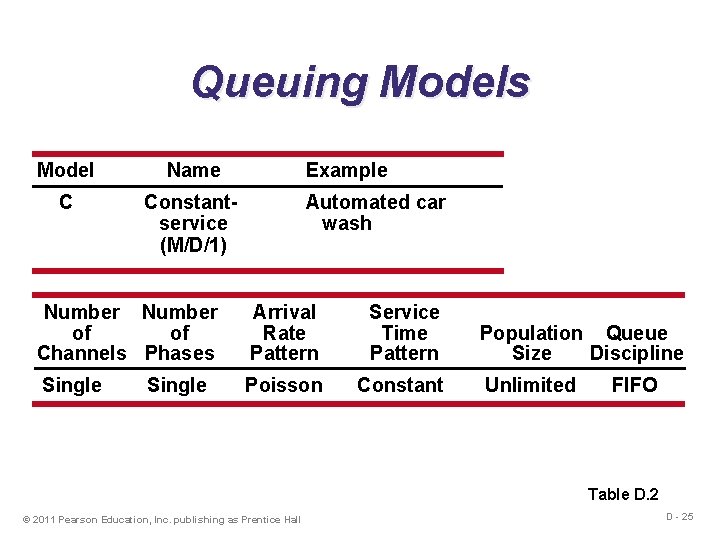
Queuing Models Model Name C Constantservice (M/D/1) Example Automated car wash Number of of Channels Phases Arrival Rate Pattern Service Time Pattern Single Poisson Constant Single Population Queue Size Discipline Unlimited FIFO Table D. 2 © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 25

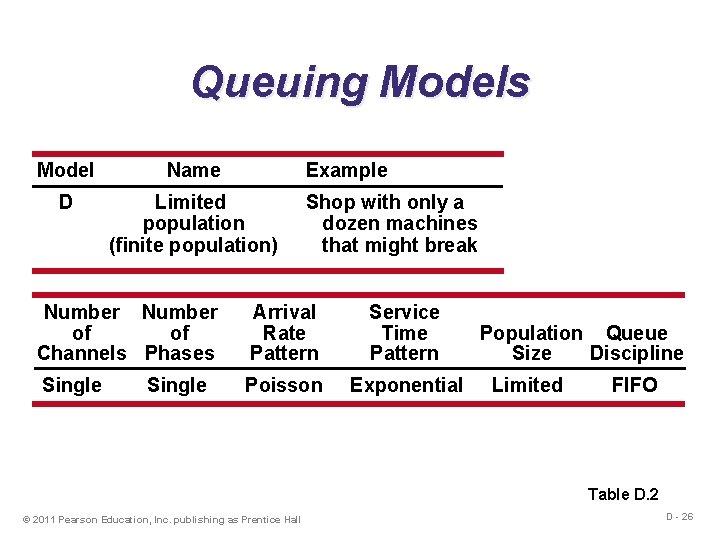
Queuing Models Model Name Example D Limited population (finite population) Shop with only a dozen machines that might break Number of of Channels Phases Arrival Rate Pattern Service Time Pattern Single Poisson Exponential Single Population Queue Size Discipline Limited FIFO Table D. 2 © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 26

Model A – Single-Channel 1. Arrivals are served on a FIFO basis and every arrival waits to be served regardless of the length of the queue 2. Arrivals are independent of preceding arrivals but the average number of arrivals does not change over time 3. Arrivals are described by a Poisson probability distribution and come from an infinite population © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 27

Model A – Single-Channel 4. Service times vary from one customer to the next and are independent of one another, but their average rate is known 5. Service times occur according to the negative exponential distribution 6. The service rate is faster than the arrival rate © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 28

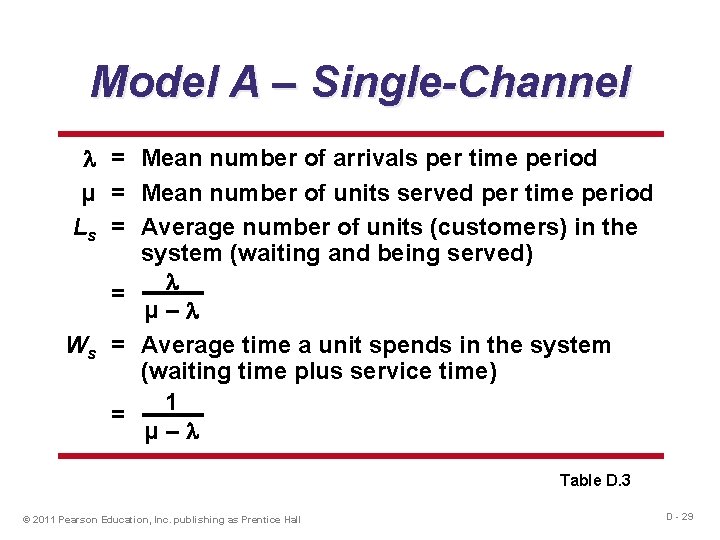
Model A – Single-Channel = Mean number of arrivals per time period µ = Mean number of units served per time period Ls = Average number of units (customers) in the system (waiting and being served) = µ– Ws = Average time a unit spends in the system (waiting time plus service time) 1 = µ– Table D. 3 © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 29

Model A – Single-Channel Lq = Average number of units waiting in the queue = Wq 2 µ(µ – ) time a unit spends waiting in the = Average queue = µ(µ – ) factor for the system = Utilization = µ © 2011 Pearson Education, Inc. publishing as Prentice Hall Table D. 3 D - 30

Model A – Single-Channel P 0 = Probability of 0 units in the system (that is, the service unit is idle) µ Pn > k=Probability of more than k units in the system, where n is the number of units in the system = 1– = µ k+1 Table D. 3 © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 31

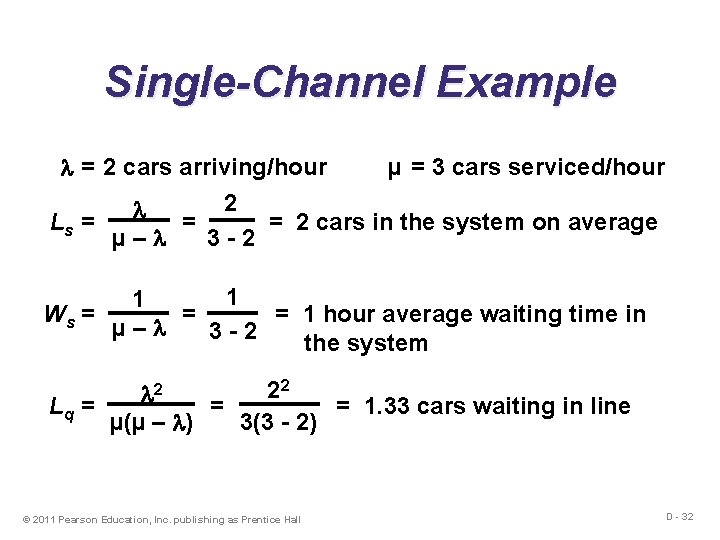
Single-Channel Example = 2 cars arriving/hour µ = 3 cars serviced/hour 2 Ls = = = 2 cars in the system on average 3 -2 µ– 1 1 Ws = = = 1 hour average waiting time in µ– 3 -2 the system 22 2 Lq = = = 1. 33 cars waiting in line 3(3 - 2) µ(µ – ) © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 32

Single-Channel Example = 2 cars arriving/hour Wq µ = 3 cars serviced/hour 2 = = = 2/3 hour = 40 minute 3(3 - 2) µ(µ – ) average waiting time = /µ = 2/3 = 66. 6% of time mechanic is busy P 0 = 1 - =. 33 probability there are 0 cars in the µ system © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 33

Single-Channel Example Probability of more than k Cars in the System k 0 1 2 3 4 5 6 7 Pn > k = (2/3)k + 1. 667 Note that this is equal to 1 - P 0 = 1 -. 33. 444. 296. 198 Implies that there is a 19. 8% chance that more than 3 cars are in the system. 132. 088. 058. 039 © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 34

Single-Channel Economics Customer dissatisfaction and lost goodwill Wq Total arrivals Mechanic’s salary Total hours customers spend waiting per day = = $10 per hour = 2/3 hour = 16 per day = $56 per day 2 2 (16) = 10 hours 3 3 Customer waiting-time cost = $10 10 2 3 = $106. 67 Total expected costs = $106. 67 + $56 = $162. 67 © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 35

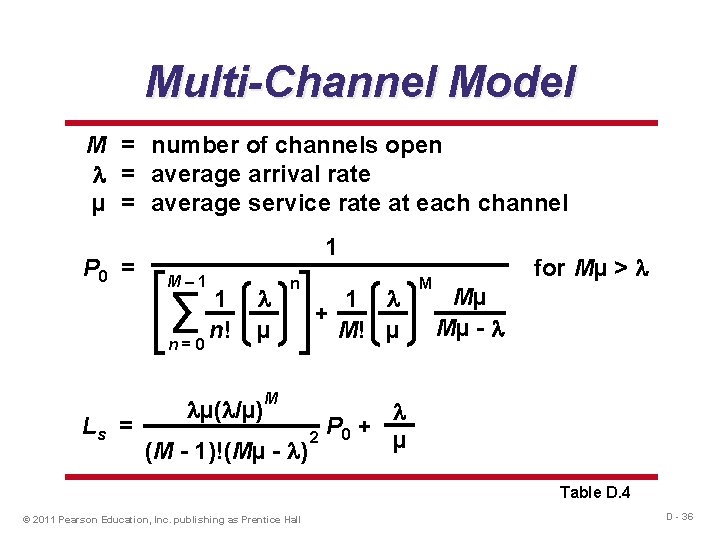
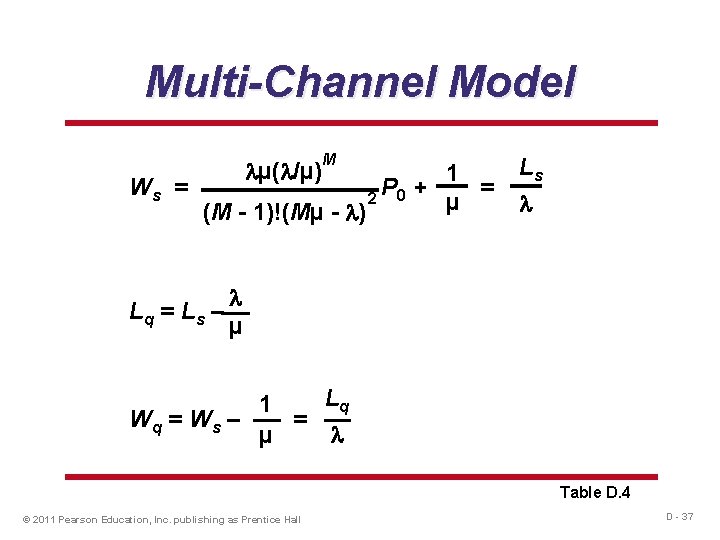
Multi-Channel Model M = number of channels open = average arrival rate µ = average service rate at each channel P 0 = 1 M– 1 ∑ 1 n! n=0 µ µ( /µ) n 1 + M! µ M for Mµ > Mµ Mµ - M Ls = P + 2 0 µ (M - 1)!(Mµ - ) Table D. 4 © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 36

Multi-Channel Model µ( /µ) M 1 Ws = P + = 2 0 µ (M - 1)!(Mµ - ) Lq = L s – Ls µ Lq 1 Wq = W s – = µ Table D. 4 © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 37

Multi-Channel Example = 2 P 0 = 1 n=0 Ws = 3/4 2 M = 2 1 ∑ Ls = µ = 3 1 n! 2 3 (2)(3(2/3)2 1! 2(3) - 2 3 = 8 2 n 1 + 2! 1 2 3 Lq = 4 © 2011 Pearson Education, Inc. publishing as Prentice Hall 2 2 3 2 + 3 2 – 3 = 2(3) 1 2 2(3) - 2 = 3 4 1 = 12 Wq = . 083 2 =. 0415 D - 38

Multi-Channel Example Single Channel Two Channels P 0 . 33 . 5 Ls 2 cars . 75 cars Ws 60 minutes 22. 5 minutes Lq 1. 33 cars . 083 cars Wq 40 minutes 2. 5 minutes © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 39

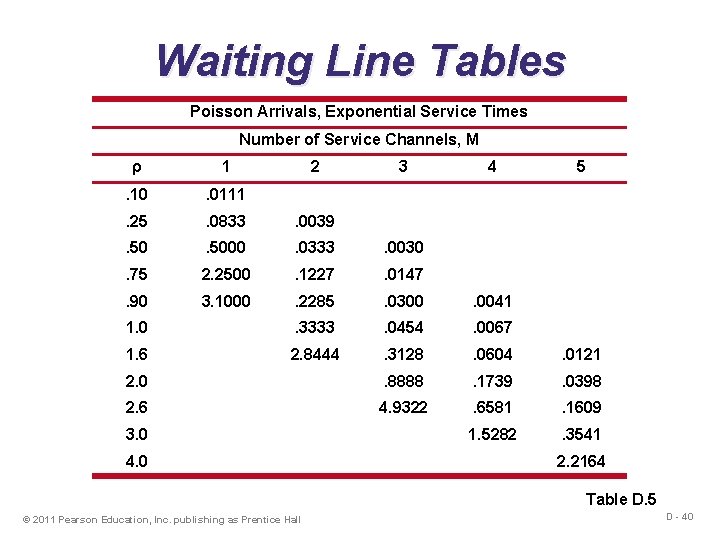
Waiting Line Tables Poisson Arrivals, Exponential Service Times Number of Service Channels, M ρ 1 2 . 10 . 0111 . 25 . 0833 . 0039 . 5000 . 0333 . 0030 . 75 2. 2500 . 1227 . 0147 . 90 3. 1000 . 2285 . 0300 . 0041 1. 0 . 3333 . 0454 . 0067 1. 6 2. 8444 . 3128 . 0604 . 0121 2. 0 . 8888 . 1739 . 0398 2. 6 4. 9322 . 6581 . 1609 1. 5282 . 3541 3. 0 4. 0 3 4 5 2. 2164 Table D. 5 © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 40

Waiting Line Table Example Bank tellers and customers = 18, µ = 20 Utilization factor = /µ =. 90 Lq Wq = From Table D. 5 Number of service windows 1 window M 1 Number in queue 8. 1 Time in queue. 45 hrs, 27 minutes 2 windows 2 . 2285 . 0127 hrs, ¾ minute 3 windows 3 . 0017 hrs, 6 seconds 4 windows 4 . 0041 . 0003 hrs, 1 second © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 41

Constant-Service Model Average length of queue 2 Lq = 2µ(µ – ) Average waiting time in queue Wq = Average number of customers in system Ls = Lq + Average time in the system 2µ(µ – ) µ Ws = Wq + 1 µ Table D. 6 © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 42

Constant-Service Example Trucks currently wait 15 minutes on average Truck and driver cost $60 per hour Automated compactor service rate (µ) = 12 trucks per hour Arrival rate ( ) = 8 per hour Compactor costs $3 per truck Current waiting cost per trip = (1/4 hr)($60) = $15 /trip 1 8 Wq = = hour 12 2(12)(12 – 8) Waiting cost/trip = (1/12 hr wait)($60/hr cost) with compactor Savings with = $15 (current) – $5(new) new equipment Cost of new equipment amortized Net savings © 2011 Pearson Education, Inc. publishing as Prentice Hall = $ 5 /trip = $10 /trip = $ 3 /trip = $ 7 /trip D - 43

Little’s Law u A queuing system in steady state L = W (which is the same as W = L/ Lq = Wq (which is the same as Wq = Lq/ u Once one of these parameters is known, the other can be easily found u It makes no assumptions about the probability distribution of arrival and service times u Applies to all queuing models except the limited population model © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 44

Limited-Population Model T T+U Average number running: J = NF(1 - X) Service factor: X = Average number waiting: L = N(1 - F) Average number being serviced: H = FNX T(1 - F) Average waiting time: W = XF Number of population: N = J + L + H Table D. 7 © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 45

Limited-Population Model D = Probability that a unit will have to wait in queue F = Efficiency factor N = Number of potential customers T = Average service time H = Average number of units being served U = Average time between unit service requirements J = Average number of units W = Average time a unit not in queue or in waits in line service bay L = Average number of units X = Service factor waiting for service M = Number of service channels © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 46

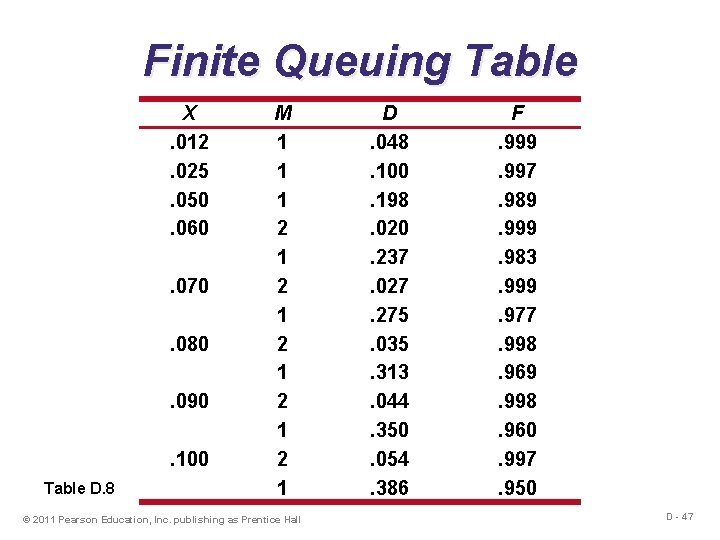
Finite Queuing Table X. 012. 025. 050. 060. 070. 080. 090. 100 Table D. 8 M 1 1 1 2 1 2 1 2 1 © 2011 Pearson Education, Inc. publishing as Prentice Hall D. 048. 100. 198. 020. 237. 027. 275. 035. 313. 044. 350. 054. 386 F. 999. 997. 989. 999. 983. 999. 977. 998. 969. 998. 960. 997. 950 D - 47

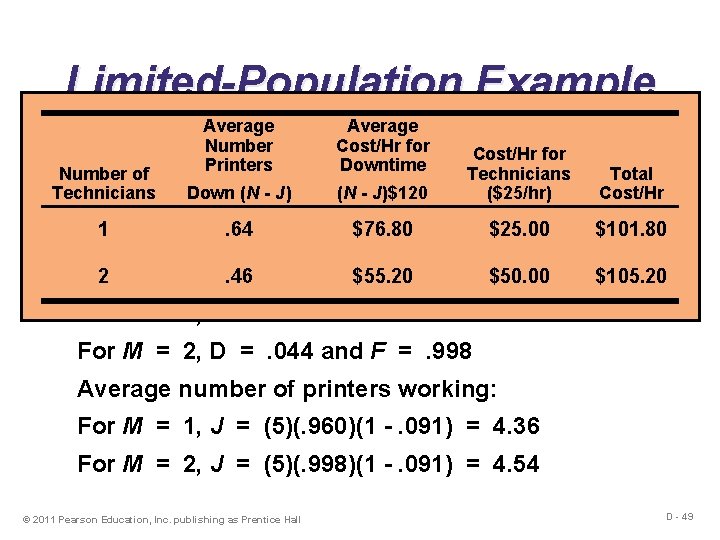
Limited-Population Example Each of 5 printers requires repair after 20 hours (U) of use One technician can service a printer in 2 hours (T) Printer downtime costs $120/hour Technician costs $25/hour 2 =. 091 (close to. 090) 2 + 20 For M = 1, D =. 350 and F =. 960 Service factor: X = For M = 2, D =. 044 and F =. 998 Average number of printers working: For M = 1, J = (5)(. 960)(1 -. 091) = 4. 36 For M = 2, J = (5)(. 998)(1 -. 091) = 4. 54 © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 48

Limited-Population Example Average Numberrequire Cost/Hr for 20 Cost/Hr Each of 5 printers repair after hours (U) for of use Printers Downtime Number Total One of technician can service a printer in 2 Technicians hours (T) Technicians Down (Ncosts - J) $120/hour (N - J)$120 ($25/hr) Cost/Hr Printer downtime Technician costs 1. 64 $25/hour $76. 80 $25. 00 $101. 80 2 =. 091 (close $55. 20 $50. 00 to. 090) $105. 20 2 + 20 For M = 1, D =. 350 and F =. 960 Service factor: 2. 46 X = For M = 2, D =. 044 and F =. 998 Average number of printers working: For M = 1, J = (5)(. 960)(1 -. 091) = 4. 36 For M = 2, J = (5)(. 998)(1 -. 091) = 4. 54 © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 49

Other Queuing Approaches u The single-phase models cover many queuing situations u Variations of the four single-phase systems are possible u Multiphase models exist for more complex situations © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 50

All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of the publisher. Printed in the United States of America. © 2011 Pearson Education, Inc. publishing as Prentice Hall D - 51