Chapter 8 Lecture Rotational Motion 2014 Pearson Education

Chapter 8 Lecture Rotational Motion © 2014 Pearson Education, Inc.

Rotational Motion • How can a star rotate 1000 times faster than a merry-go-round? • Why is it more difficult to balance on a stopped bike than on a moving bike? • How is the Moon slowing Earth's rate of rotation? © 2014 Pearson Education, Inc.

What's new in this chapter • In the last chapter, we learned about the torque that a force can exert on a rigid body. – We analyzed only rigid bodies that were in static equilibrium. • In this chapter, we learn how to describe, explain, and predict motion for objects that rotate. – For example, the hip joint and a car tire © 2014 Pearson Education, Inc.

8. 1 Rotational Kinematics © 2014 Pearson Education, Inc.

Rotational Kinematics © 2014 Pearson Education, Inc.

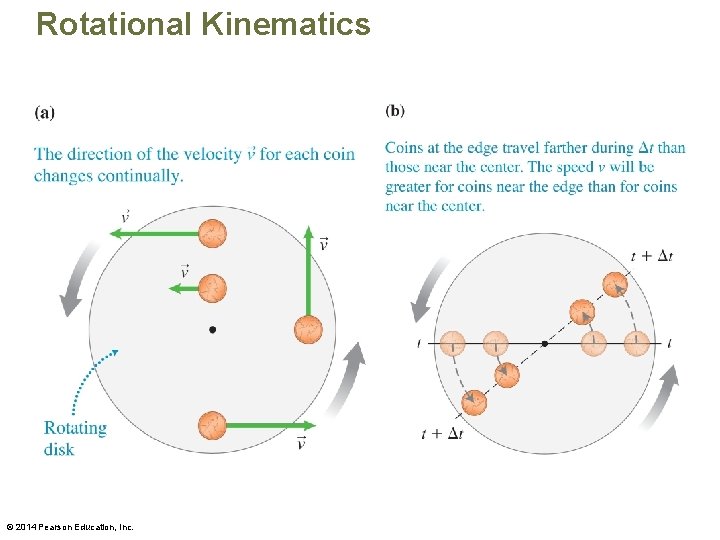
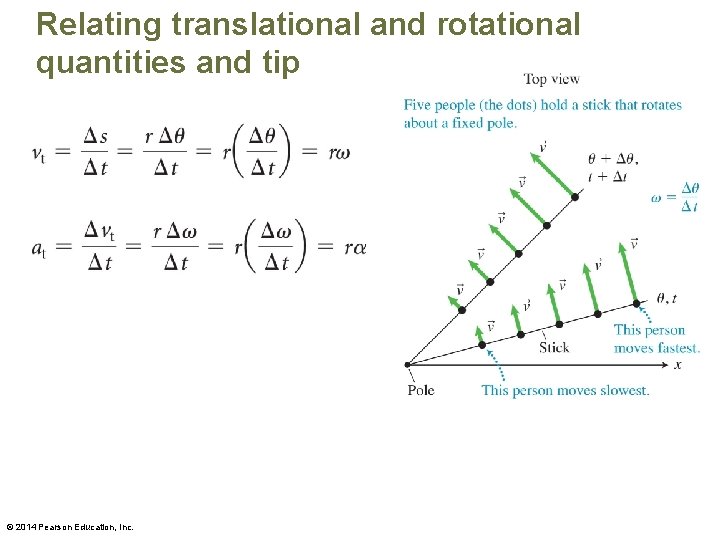
Rotational kinematics • Imagine that you place small coins at different locations on the disk: – The direction of the velocity of each coin changes continually. – A coin that sits closer to the edge moves faster and covers a longer distance than a coin placed closer to the center. • Different parts of the disk move in different directions and at different speeds! © 2014 Pearson Education, Inc.

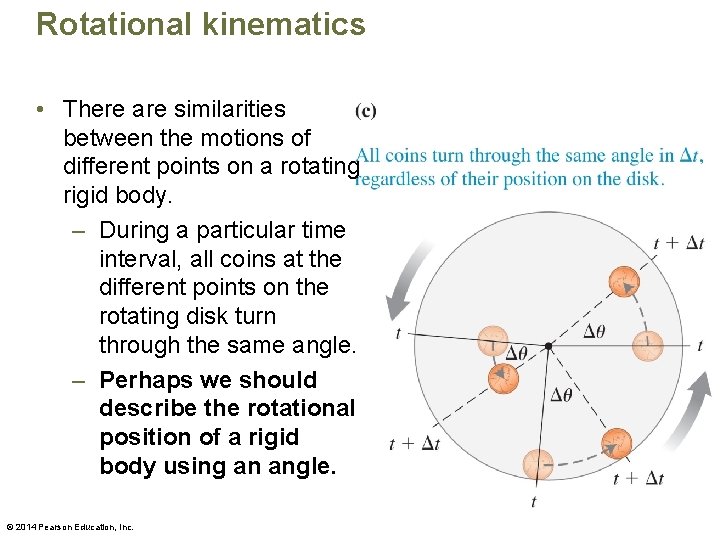
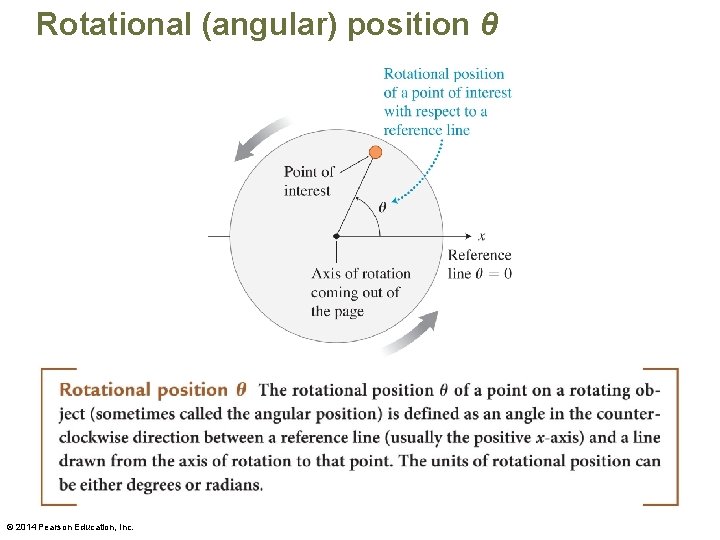
Rotational kinematics • There are similarities between the motions of different points on a rotating rigid body. – During a particular time interval, all coins at the different points on the rotating disk turn through the same angle. – Perhaps we should describe the rotational position of a rigid body using an angle. © 2014 Pearson Education, Inc.

Rotational (angular) position θ © 2014 Pearson Education, Inc.

Units of rotational position • The unit for rotational position is the radian (rad). It is defined in terms of: – The arc length s – The radius r of the circle • The angle in units of radians is the ratio of s and r: • The radian unit has no dimensions; it is the ratio of two lengths. The unit rad is just a reminder that we are using radians for angles. 1 Radian = 57. 30. © 2014 Pearson Education, Inc.

Tip Figure 8. 4 © 2014 Pearson Education, Inc.

Tip © 2014 Pearson Education, Inc.

Conversion Deg to Rad • Comparing degrees and radians • • Converting from degrees to radians • Converting from radians to degrees © 2014 Pearson Education, Inc.

Rotational (angular) velocity ω • Translational velocity is the rate of change of linear position. • We define the rotational (angular) velocity v of a rigid body as the rate of change of each point's rotational position. – All points on the rigid body rotate through the same angle in the same time, so each point has the same rotational velocity. © 2014 Pearson Education, Inc.

Rotational (angular) velocity ω © 2014 Pearson Education, Inc.

Tips © 2014 Pearson Education, Inc.

Rotational (angular) acceleration α • Translational acceleration describes an object's change in velocity for linear motion. – We could apply the same idea to the center of mass of a rigid body that is moving as a whole from one position to another. • The rate of change of the rigid body's rotational velocity is its rotational acceleration. – When the rotation rate of a rigid body increases or decreases, it has a nonzero rotational acceleration. © 2014 Pearson Education, Inc.

Rotational (angular) acceleration α © 2014 Pearson Education, Inc.

Tip © 2014 Pearson Education, Inc.

Relating translational and rotational quantities and tip © 2014 Pearson Education, Inc.

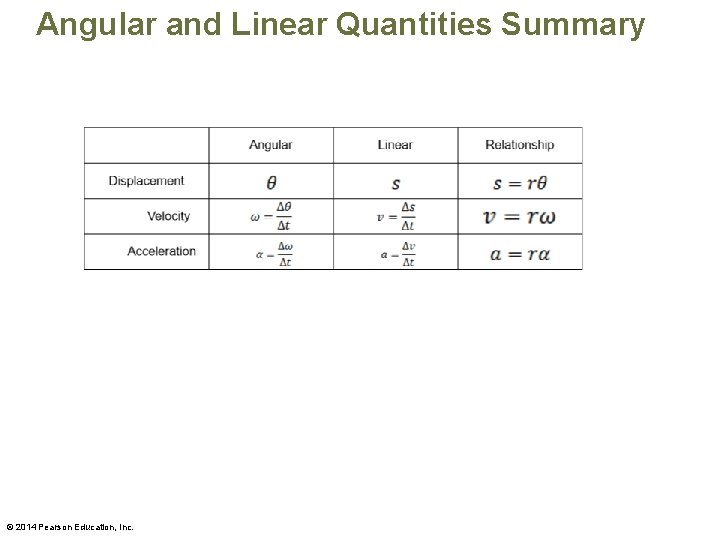
Angular and Linear Quantities Summary © 2014 Pearson Education, Inc.

Quantitative Exercise 8. 2 • Determine the tangential speed of a stable gaseous cloud around a black hole. • The cloud has a stable circular orbit at its innermost 30 -km radius. This cloud moves in a circle about the black hole about 970 times per second. © 2014 Pearson Education, Inc.

Rotational motion at constant acceleration • • θ 0 is an object's rotational position at t 0 = 0. ω0 is an object's rotational velocity at t 0 = 0. θ and ω are the rotational position and the rotational velocity at some later time t. α is the object's constant rotational acceleration during the time interval from time 0 to time t. © 2014 Pearson Education, Inc.

Rotational motion at constant acceleration • Rotational position θ is positive if the object is rotating counterclockwise and negative if it is rotating clockwise. • Rotational velocity ω is positive if the object is rotating counterclockwise and negative if it is rotating clockwise. • The sign of the rotational acceleration α depends on how the rotational velocity is changing: – α has the same sign as ω if the magnitude of ω is increasing. – α has the opposite sign of ω if the magnitude of ω is decreasing. © 2014 Pearson Education, Inc.

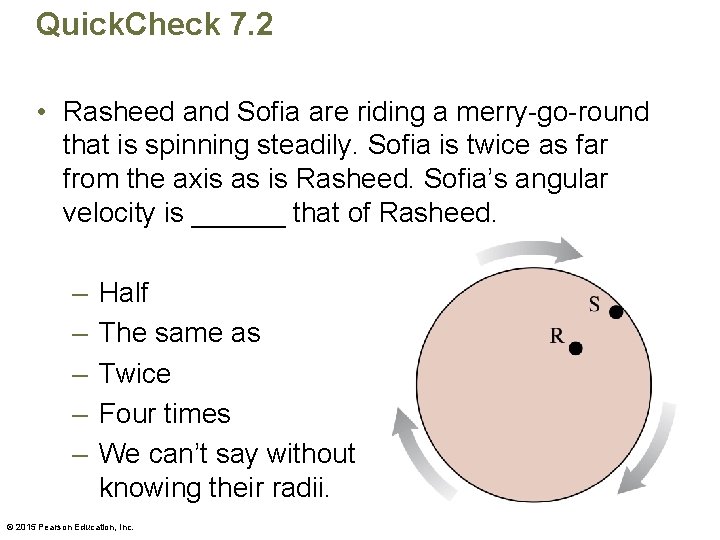
Quick. Check 7. 2 • Rasheed and Sofia are riding a merry-go-round that is spinning steadily. Sofia is twice as far from the axis as is Rasheed. Sofia’s angular velocity is ______ that of Rasheed. – – – Half The same as Twice Four times We can’t say without knowing their radii. © 2015 Pearson Education, Inc.

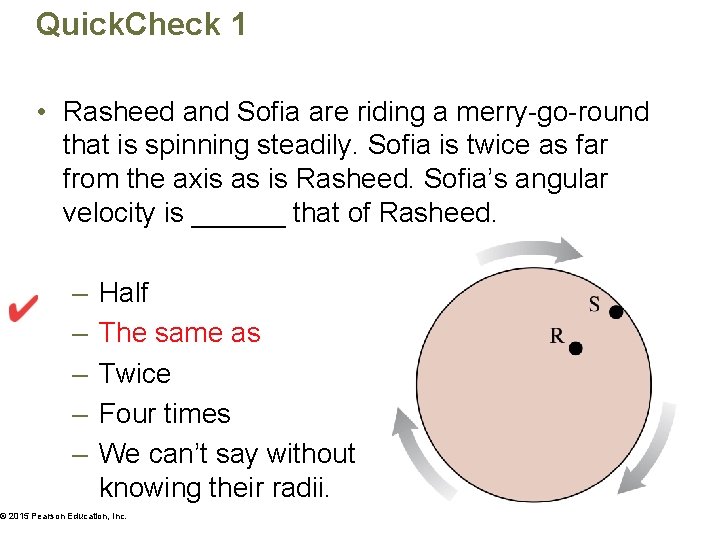
Quick. Check 1 • Rasheed and Sofia are riding a merry-go-round that is spinning steadily. Sofia is twice as far from the axis as is Rasheed. Sofia’s angular velocity is ______ that of Rasheed. – – – Half The same as Twice Four times We can’t say without knowing their radii. © 2015 Pearson Education, Inc.

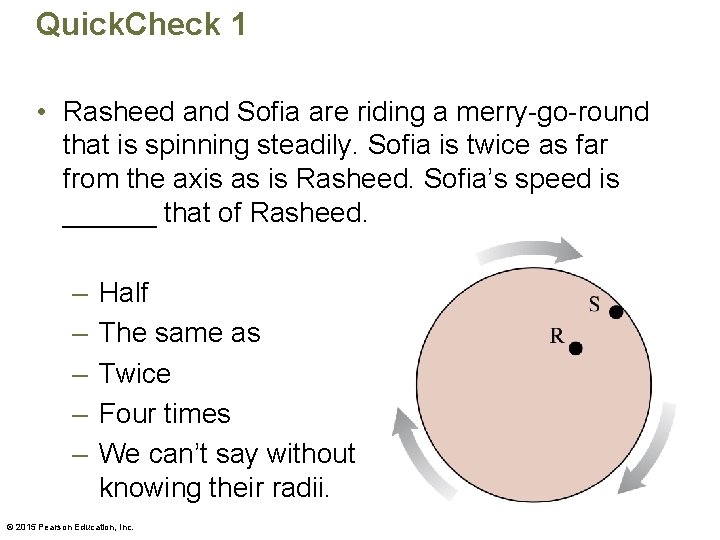
Quick. Check 1 • Rasheed and Sofia are riding a merry-go-round that is spinning steadily. Sofia is twice as far from the axis as is Rasheed. Sofia’s speed is ______ that of Rasheed. – – – Half The same as Twice Four times We can’t say without knowing their radii. © 2015 Pearson Education, Inc.

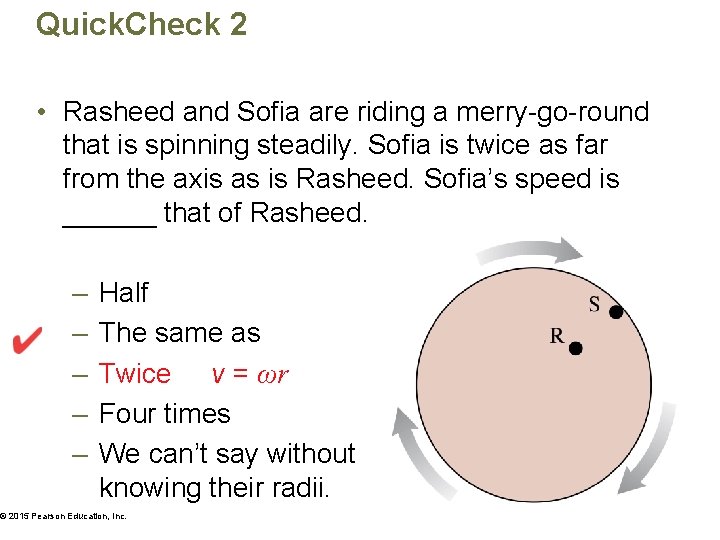
Quick. Check 2 • Rasheed and Sofia are riding a merry-go-round that is spinning steadily. Sofia is twice as far from the axis as is Rasheed. Sofia’s speed is ______ that of Rasheed. – – – Half The same as Twice v = ωr Four times We can’t say without knowing their radii. © 2015 Pearson Education, Inc.

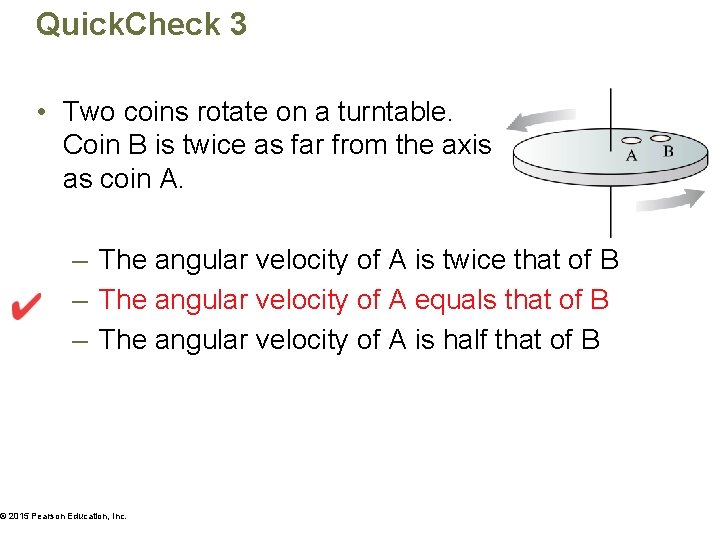
Quick. Check 2 • Two coins rotate on a turntable. Coin B is twice as far from the axis as coin A. – The angular velocity of A is twice that of B – The angular velocity of A equals that of B – The angular velocity of A is half that of B © 2015 Pearson Education, Inc.

Quick. Check 3 • Two coins rotate on a turntable. Coin B is twice as far from the axis as coin A. – The angular velocity of A is twice that of B – The angular velocity of A equals that of B – The angular velocity of A is half that of B © 2015 Pearson Education, Inc.

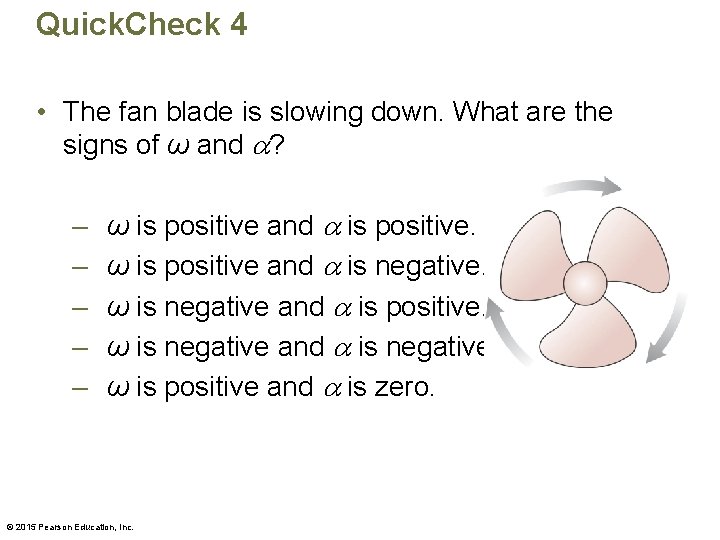
Quick. Check 4 • The fan blade is slowing down. What are the signs of ω and ? – – – ω is positive and is positive. ω is positive and is negative. ω is negative and is positive. ω is negative and is negative. ω is positive and is zero. © 2015 Pearson Education, Inc.

Quick. Check 4 • The fan blade is slowing down. What are the signs of ω and ? – – – ω is positive and is positive. ω is positive and is negative. ω is negative and is positive. ω is negative and is negative. ω is positive and is zero. “Slowing down” means that and have opposite signs, not that is negative. © 2015 Pearson Education, Inc.

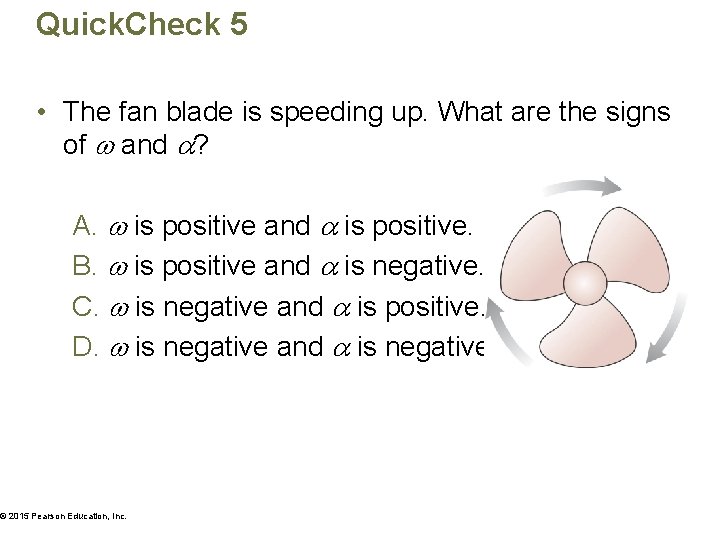
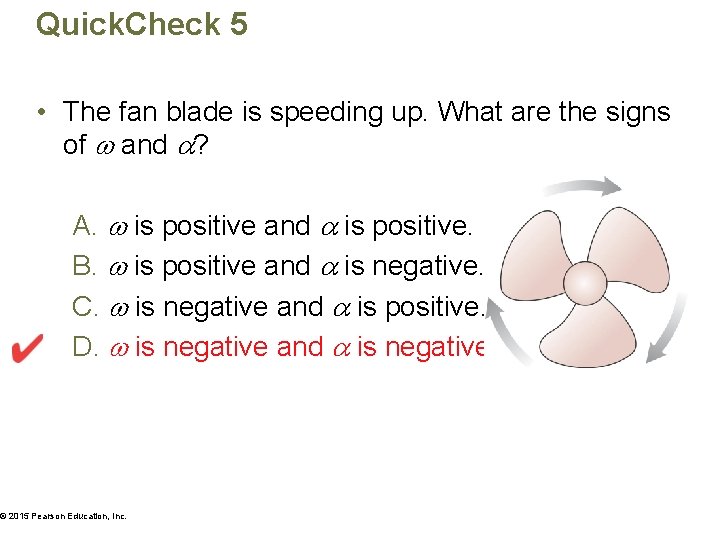
Quick. Check 5 • The fan blade is speeding up. What are the signs of and ? A. is positive and is positive. B. is positive and is negative. C. is negative and is positive. D. is negative and is negative. © 2015 Pearson Education, Inc.

Quick. Check 5 • The fan blade is speeding up. What are the signs of and ? A. is positive and is positive. B. is positive and is negative. C. is negative and is positive. D. is negative and is negative. © 2015 Pearson Education, Inc.

Three Types of Acceleration © 2014 Pearson Education, Inc.

Three Types of Acceleration © 2014 Pearson Education, Inc.

Three Types of Acceleration • We now have three accelerations associated with a rigid rotating body: tangential, angular and centripetal, or a. T, α, and a. C. • And they are all related to each other - can you express all three of these accelerations in terms of the angular velocity of the rotating object? © 2014 Pearson Education, Inc.

Total Linear Accleration © 2014 Pearson Education, Inc.

Don’t Forget Therefore: © 2014 Pearson Education, Inc.

Quick Problems Answers 1. a 2. d and 3. c © 2014 Pearson Education, Inc.

Quick Problems Answers 1. d 2. b © 2014 Pearson Education, Inc.

Quick Problems Answers 1. d 2. c 3. c © 2014 Pearson Education, Inc.

Quick Problems An old phonograph record revolves at 45 rpm. 1. What is its angular velocity in rad/sec? ω = 45 rev/min = 45 (2π/60 radians/sec) = 4. 71 rad/sec 2. Once the motor is turned off, it takes 0. 75 seconds to come to a stop. What is its average angular acceleration? givens: ωf = 0, ωo = 4. 71 rad/sec, t = 0. 75 seconds. using the equation ωf = ωo + αt we can determine that α = (0 - 4. 71)/0. 75 = -6. 28 rad/sec 2

Quick Problems 3. How many revolutions did it make while coming to a stop? using the equation θ = ½(ωf + ωo)t we can determine that θ = ½ (0 + 4. 71) 0. 75 θ = 1. 77 radians since there are 2π radians in every revolution, θ = 0. 281 rev.

Quick Problems 4. A fan is turning at 10 rev/min and then speeds up to 25 rev/min in 10 seconds. a. How many revolutions does the blade require to alter its speed? using the equation θ = ½(ωf + ωo)t we can determine that θ = ½(1. 05 + 2. 63)10 θ = 18. 4 radians since there are 2π radians in every revolution, θ = 2. 92 rev b. If the tip of one blade is 30 cm from the center, what is the final tangential velocity of the tip? using the equation v = rω allows us to determine that v = (0. 30)(2. 63) v = 0. 789 m/sec

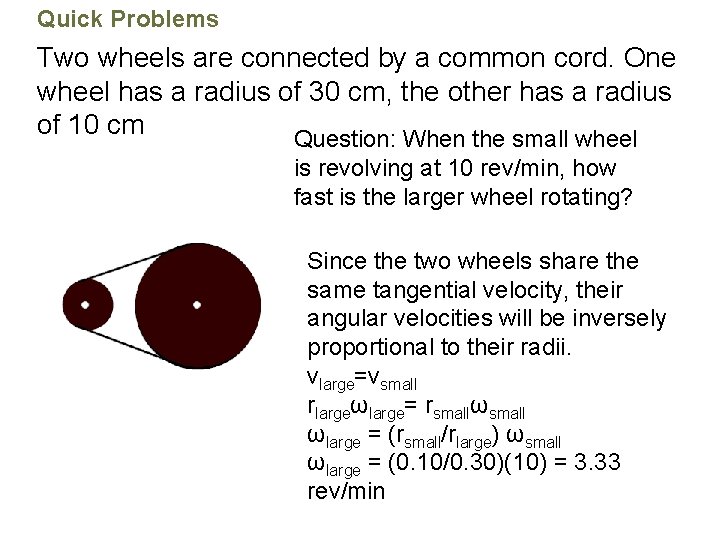
Quick Problems Two wheels are connected by a common cord. One wheel has a radius of 30 cm, the other has a radius of 10 cm Question: When the small wheel is revolving at 10 rev/min, how fast is the larger wheel rotating? Since the two wheels share the same tangential velocity, their angular velocities will be inversely proportional to their radii. vlarge=vsmall rlargeωlarge= rsmallωsmall ωlarge = (rsmall/rlarge) ωsmall ωlarge = (0. 10/0. 30)(10) = 3. 33 rev/min

8. 2 Torque and Rotational Acceleration

Rotational Dynamics or Newtons 2 nd Law for Rotation Just like there are rotational analogs for Kinematics, there are rotational analogs for Dynamics. Kinematics allowed us to solve for the motion of objects, without caring why or how they moved. Dynamics showed how the application of forces causes motion and this is summed up in Newton's Three Laws. These laws also apply to rotational motion. The rotational analogs to Newton's Laws will be presented now.

Rotational Dynamics What causes a rigid body to have rotational acceleration? In the previous chapters…When we discussed acceleration we used point-like objects interactions with each other…and those interaction cause forces which resulted in acceleration (linear translational acclerations). With rotational accelerations we need to look at rigid bodies/extended body instead of point objects Rotation is caused by torque. Last chapter we analyzed rigid bodies in static equilibrium. In this chapter its all about net torque not being equal to zero.

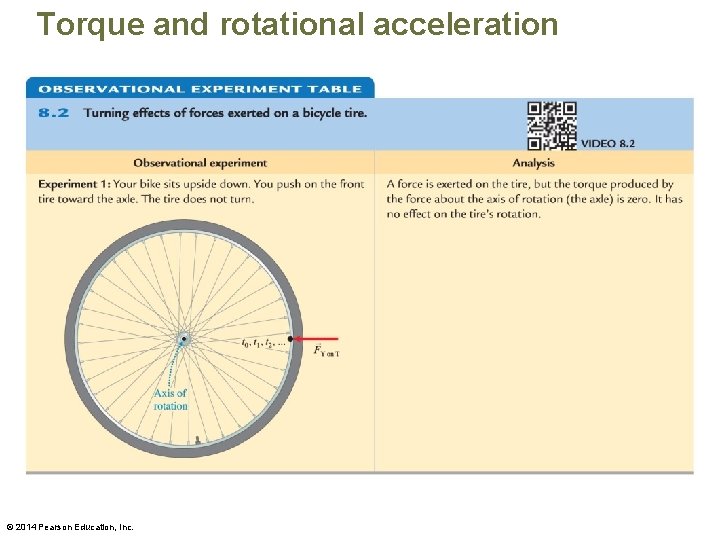
Torque and rotational acceleration © 2014 Pearson Education, Inc.

Torque and rotational acceleration © 2014 Pearson Education, Inc.

Torque and rotational acceleration © 2014 Pearson Education, Inc.

Torque and rotational acceleration © 2014 Pearson Education, Inc.

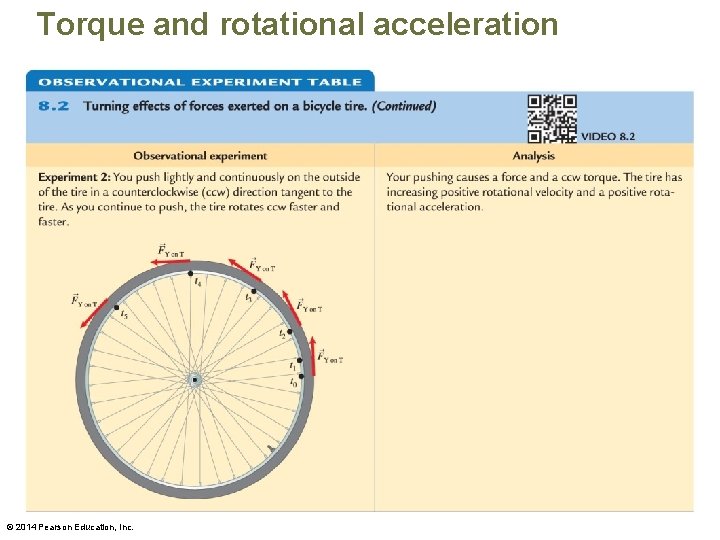
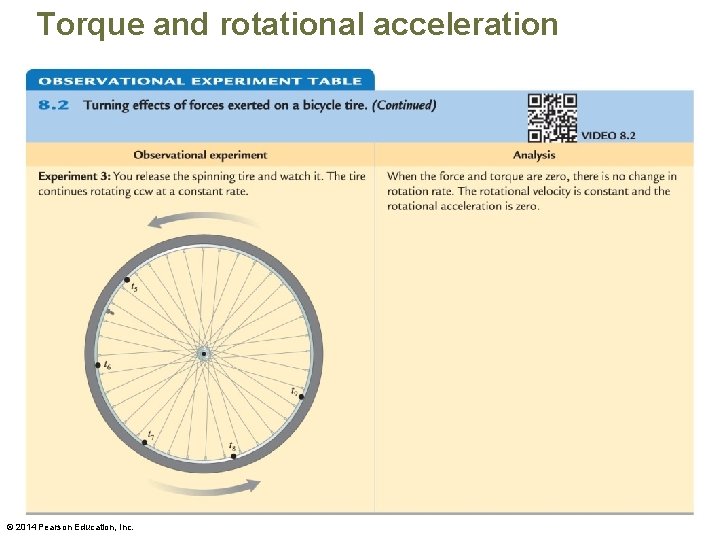
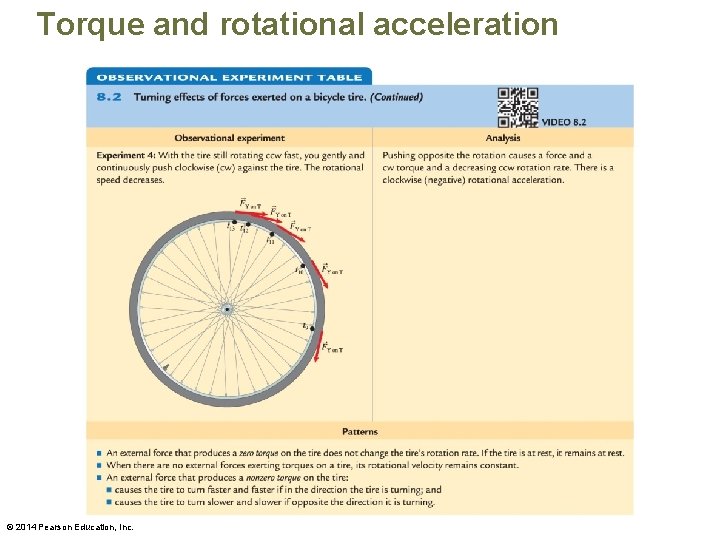
Torque and rotational acceleration • The experiments indicate a zero torque has no effect on rotational motion but a nonzero torque does cause a change. – If the torque is in the same direction as the direction of rotation of the rigid body, the object's rotational speed increases. – If the torque is in the opposite direction, the object's speed decreases. © 2014 Pearson Education, Inc.

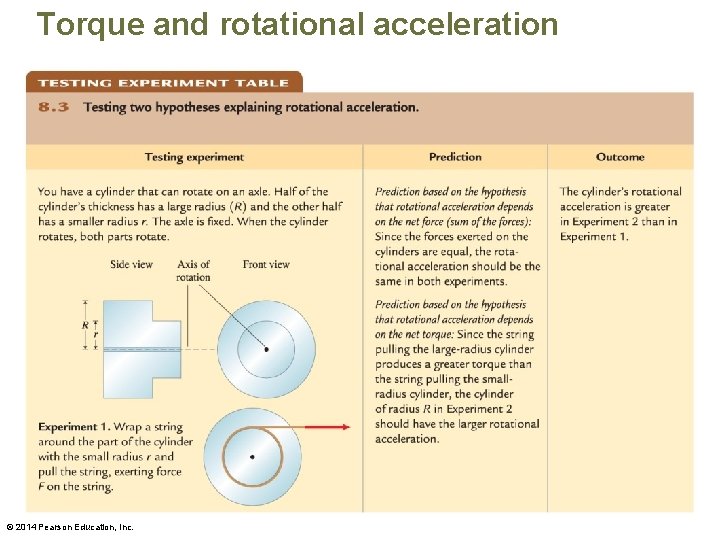
Torque and rotational acceleration • Our goal is to determine which physical quantities cause rotational acceleration of an extended object. There are two possibilities: 1. The sum of the forces (net force) exerted on the object or 2. The net torque caused by the forces • Testing experiments help us determine which (if either) of these quantities might affect rotational acceleration. © 2014 Pearson Education, Inc.

Torque and rotational acceleration © 2014 Pearson Education, Inc.

Torque and rotational acceleration © 2014 Pearson Education, Inc.

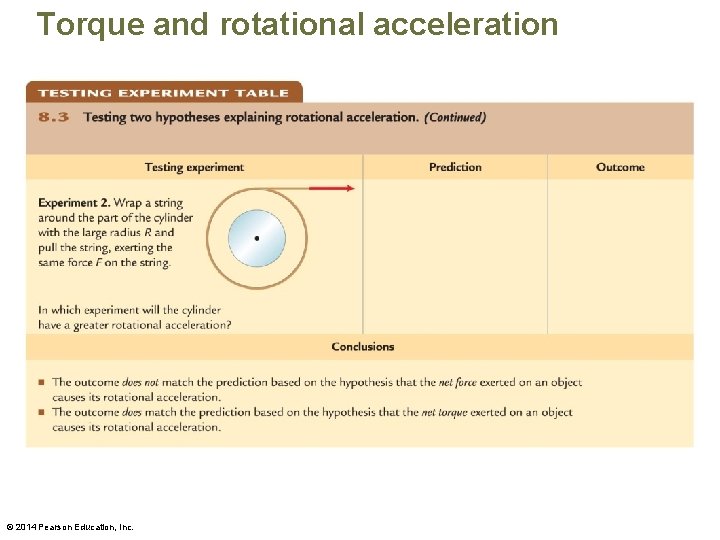
Torque and rotational acceleration • This is similar to what we learned when studying translational motion. A nonzero net force needs to be exerted on an object to cause its velocity to change. The greater the net force, the greater the translational acceleration of the object. • NET TORQUE IS THE CAUSE OF ANGULAR ACCELERATION (JUST LIKE FORCE IS FOR ACCELERATION) © 2014 Pearson Education, Inc.

Torque and rotational acceleration • So far all experiments in this chapter have been performed with a rigid body fixed axis at its center of mass (Not free to move linearly) • If a rigid body was not held fixed, then a change in both translational and rotational motion could occur. • The translational acceleration of center of mass of such an object is determined by Newtons Second law ΣF=ma. (More on this later) • The rotational acceleration around its center of mass will be determined by the next few slides. © 2014 Pearson Education, Inc.

8. 3 Rotational Inertia (Broomstick Demo) © 2014 Pearson Education, Inc.

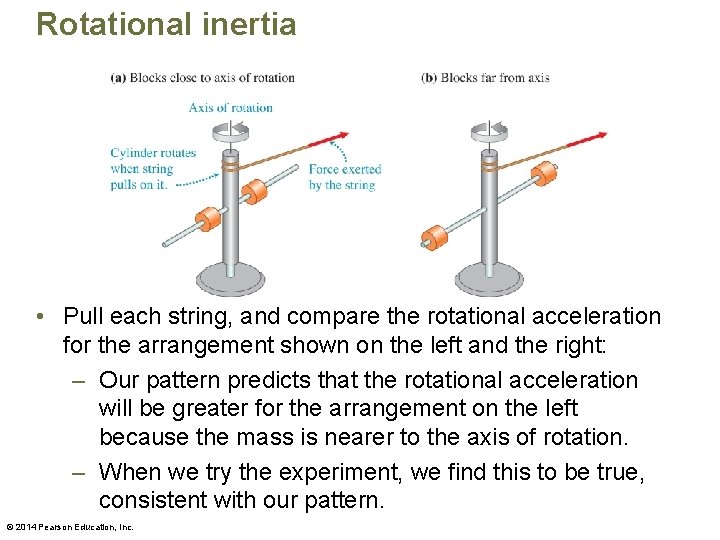
Rotational inertia © 2014 Pearson Education, Inc.

Rotational inertia • Pull each string, and compare the rotational acceleration for the arrangement shown on the left and the right: – Our pattern predicts that the rotational acceleration will be greater for the arrangement on the left because the mass is nearer to the axis of rotation. – When we try the experiment, we find this to be true, consistent with our pattern. © 2014 Pearson Education, Inc.

Rotational inertia • Rotational inertia is the physical quantity characterizing the location of the mass relative to the axis of rotation of the object. – The closer the mass of the object is to the axis of rotation, the easier it is to change its rotational motion and the smaller its rotational inertia. – The magnitude depends on both the total mass of the object and the distribution of that mass about its axis of rotation. © 2014 Pearson Education, Inc.

nd 2 8. 4 Newtons Law For Rotational Motion © 2014 Pearson Education, Inc.

Newtons 2 nd Law for Rotational Motion • Development of relationship between – α (rotational accelerations) – ∑Ƭ (net torque) – Rotational Inertia • Push block with finger exert a FF/B tangent to the circular path • Push Causes a torque that turns the block increasing rotational velocity. • Torque Produces: © 2014 Pearson Education, Inc.

Newtons 2 nd Law for Rotational Motion © 2014 Pearson Education, Inc.

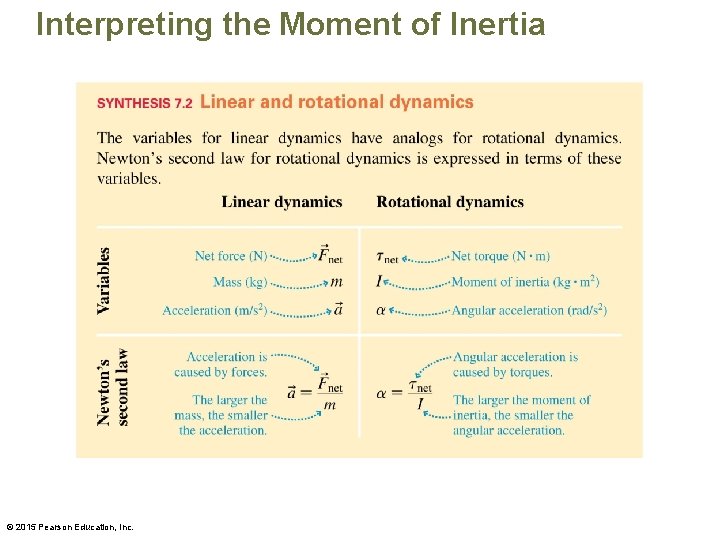
Analogy between translational motion and rotational motion © 2014 Pearson Education, Inc.

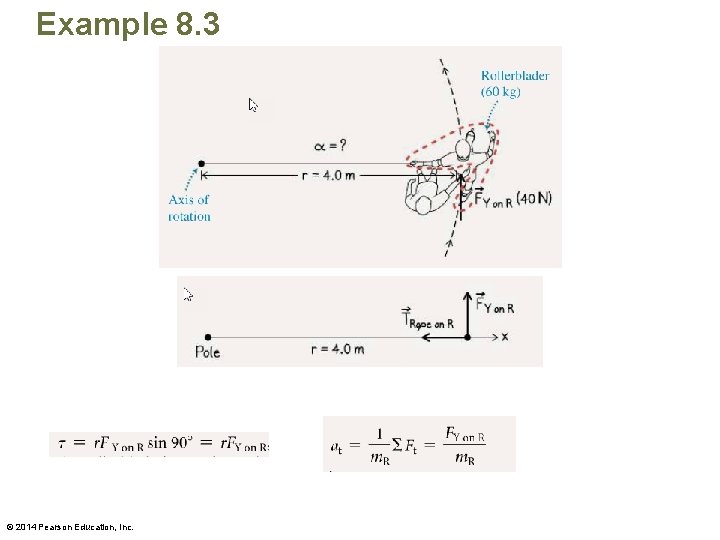
Example 8. 3 • A 60 -kg rollerblader holds a 4. 0 -m-long rope that is loosely tied around a metal pole. You push the rollerblader, exerting a 40 -N force on her, which causes her to move increasingly more rapidly in a counterclockwise circle around the pole. The surface she skates on is smooth, and the wheels of her rollerblades are well oiled. Determine the tangential and rotational acceleration of the rollerblader. © 2014 Pearson Education, Inc.

Example 8. 3 © 2014 Pearson Education, Inc.

Example 8. 3 © 2014 Pearson Education, Inc.

Example 8. 3 Homework: Complete the try it yourself problem. Submit tomorrow. © 2014 Pearson Education, Inc.

Newton 2 nd Law For Rotational Motion Applied to Rigid Bodies • © 2014 Pearson Education, Inc.

Newton's second law for rotational motion applied to rigid bodies • The rotational inertia of a rigid body about some axis of rotation is the sum of the rotational inertias of the individual point-like objects that make up the rigid body. – The rotational inertia of this two-block rigid body is twice the rotational inertia of the single block. © 2014 Pearson Education, Inc.

We are going to use I to represent Rotational Inertia I=mr 2 Therefore rotational inertia of a rigid body consists of several point like parts located at different distances from the axis of rotation is the sum of the mr 2 terms for each part © 2014 Pearson Education, Inc.

Quantitative Exercise 8. 4 1. Each block of mass contributes differently ot the rotational inertia of the system (further away from axis of rotation © 2014 Pearson Education, Inc.

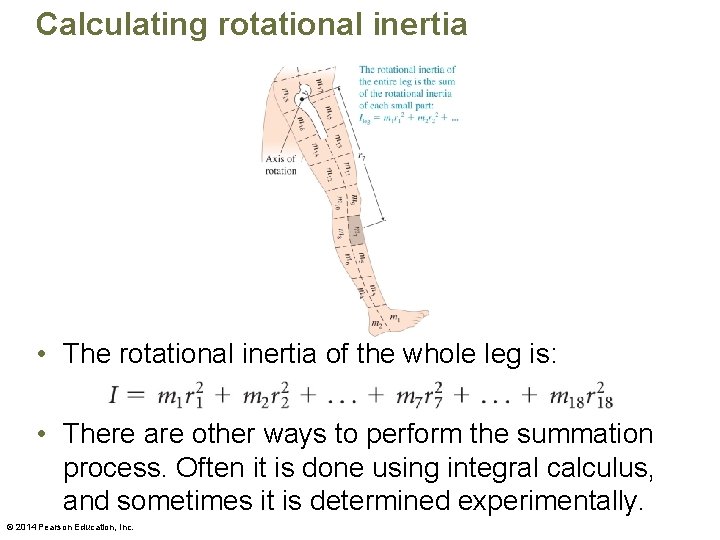
Calculating rotational inertia • The rotational inertia of the whole leg is: • There are other ways to perform the summation process. Often it is done using integral calculus, and sometimes it is determined experimentally. © 2014 Pearson Education, Inc.

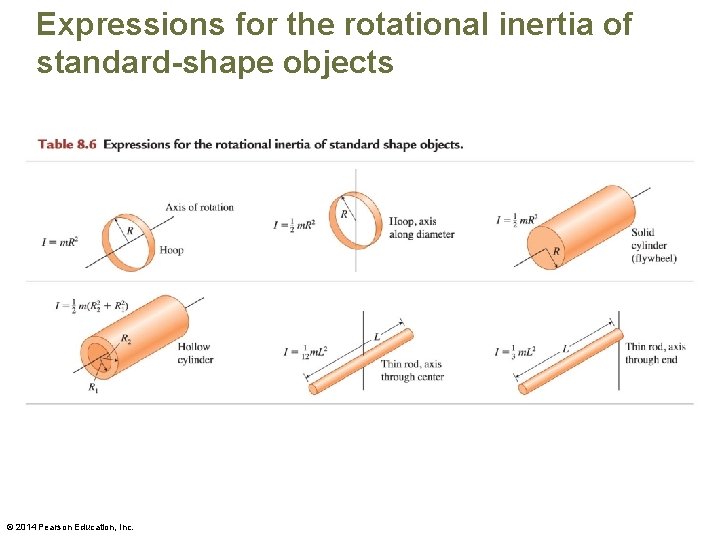
Expressions for the rotational inertia of standard-shape objects © 2014 Pearson Education, Inc.

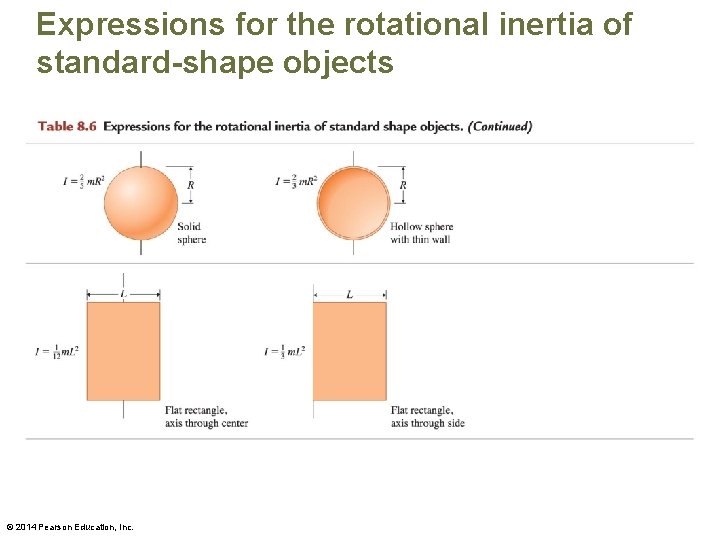
Expressions for the rotational inertia of standard-shape objects © 2014 Pearson Education, Inc.

Rotational form of Newton's second law © 2014 Pearson Education, Inc.

Tip © 2014 Pearson Education, Inc.

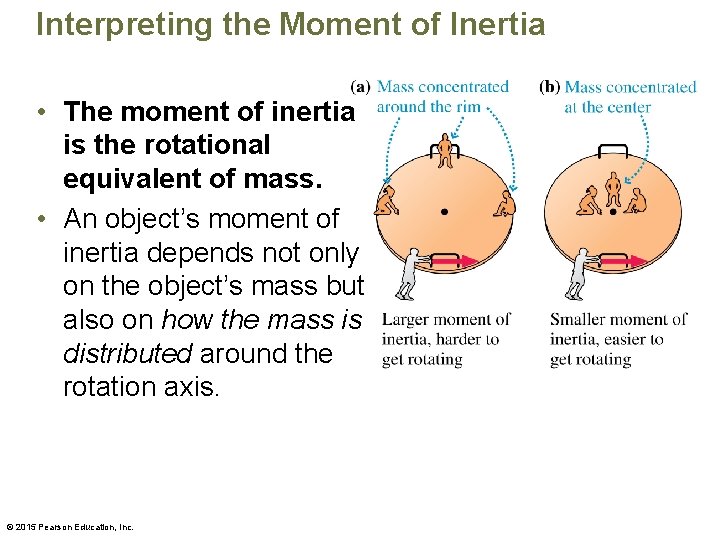
Interpreting the Moment of Inertia • The moment of inertia is the rotational equivalent of mass. • An object’s moment of inertia depends not only on the object’s mass but also on how the mass is distributed around the rotation axis. © 2015 Pearson Education, Inc.

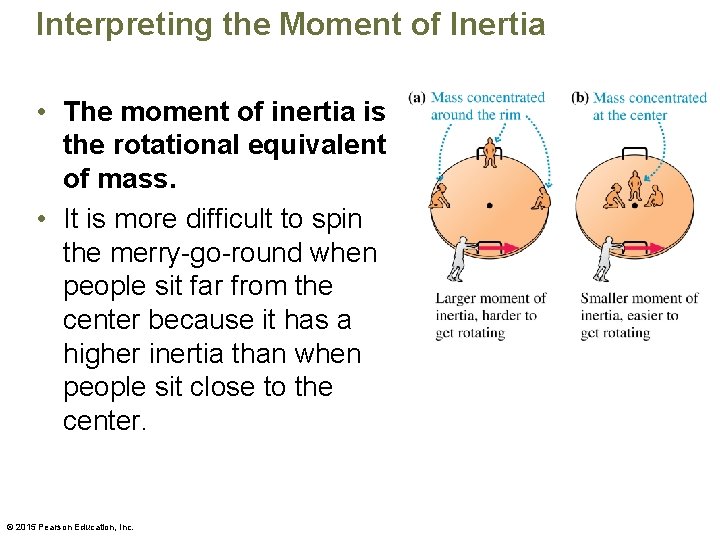
Interpreting the Moment of Inertia • The moment of inertia is the rotational equivalent of mass. • It is more difficult to spin the merry-go-round when people sit far from the center because it has a higher inertia than when people sit close to the center. © 2015 Pearson Education, Inc.

Interpreting the Moment of Inertia © 2015 Pearson Education, Inc.

Constraints Due to Ropes and Pulleys • If the pulley turns without the rope slipping on it then the rope’s speed must exactly match the speed of the rim of the pulley. • The attached object must have the same speed and acceleration as the rope. © 2015 Pearson Education, Inc.

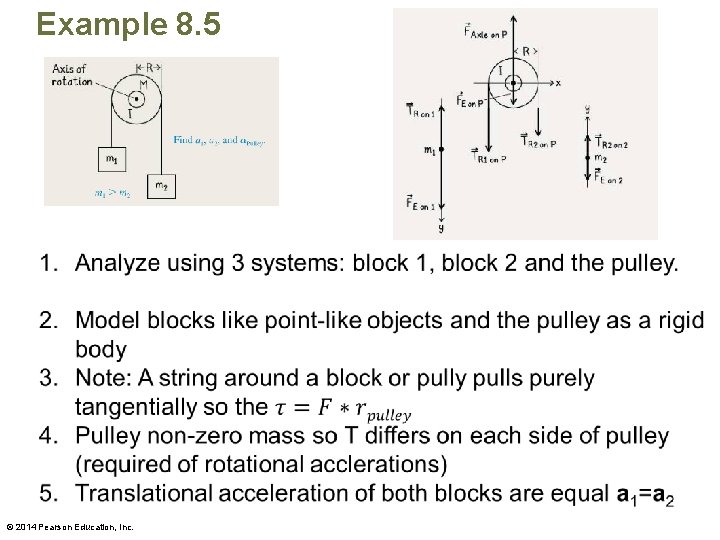
Example 8. 5 • In an Atwood machine, a block of mass m 1 and a less massive block of mass m 2 are connected by a string that passes over a pulley of mass M and radius R. • What are the translational accelerations a 1 and a 2 of the two blocks and the rotational acceleration α of the pulley? © 2014 Pearson Education, Inc.

Example 8. 5 © 2014 Pearson Education, Inc.

Example 8. 5 • The translational acceleration of the hanging objects is due to the difference between the gravitational force that Earth exerts on them and the tension force that the string exerts on them. • The rotational acceleration of the pulley is due to a nonzero net torque produced by the two tension forces exerted on the pulley. • We consider the pulley to be similar to a solid cyl inder. Then according to Table 8. 6, its rotational inertia around the axis that passes through its center is I = -1 MR 2, where R is the radius of the pulley and M is its mass. © 2014 Pearson Education, Inc.

Example 8. 5 © 2014 Pearson Education, Inc.

Example 8. 5 © 2014 Pearson Education, Inc.

Example 8. 5 Ok I want you to complete for HW tonight Exercise 8. 5 Try it yourself. The answers are provide. Hand in Tomorrow!!! © 2014 Pearson Education, Inc.

Example 8. 6 (Complete at Home its in the book) • A woman tosses a 0. 80 -kg soft-drink bottle vertically upward to a friend on a balcony above. At the beginning of the toss, her forearm rotates upward from the horizontal so that her hand exerts a 20 -N upward force on the bottle. Determine the force that her biceps exerts on her forearm during this initial instant of the throw. The mass of her forearm is 0. 65 kg and its rotational inertia about the elbow joint is 0. 044 kg • m 2. The attachment point of the biceps muscle is 5. 0 cm from the elbow joint, the hand is 35 cm away from the elbow, and the center of mass of the forearm/hand is 16 cm from the elbow. © 2014 Pearson Education, Inc.

8. 5 Rotational Momentum © 2014 Pearson Education, Inc.

Rotational momentum © 2014 Pearson Education, Inc.

Rotational momentum © 2014 Pearson Education, Inc.

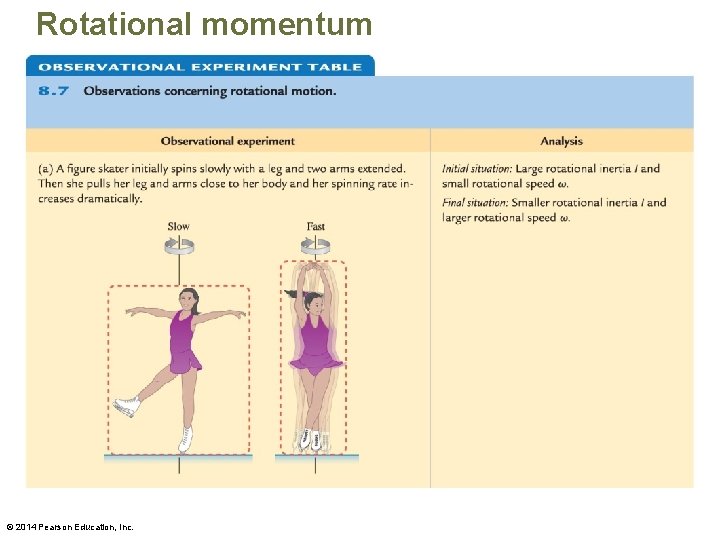
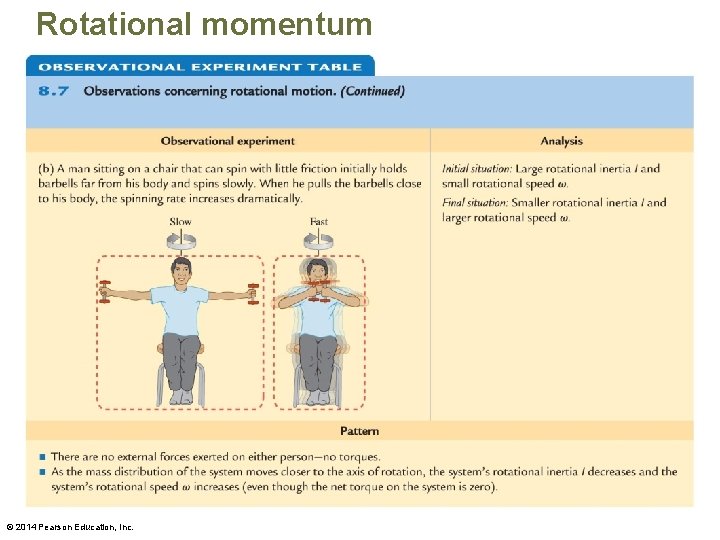
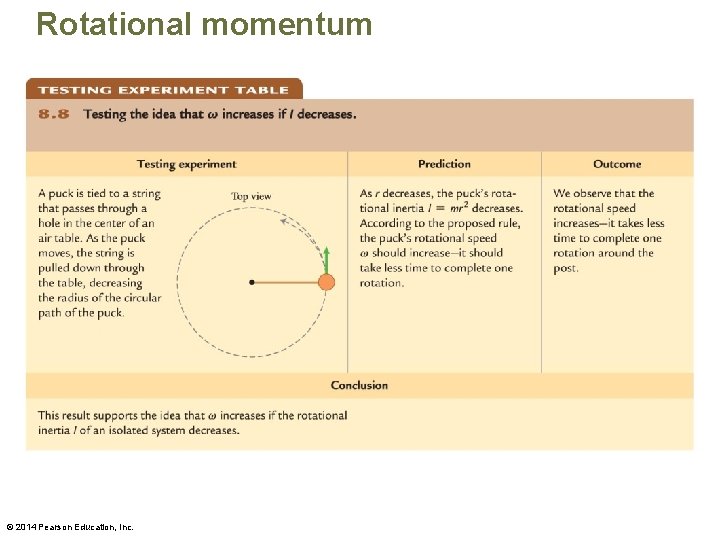
Rotational momentum • For each experiment, the rotational inertia of the spinning person decreased (the mass moved closer to the axis of rotation). Simultaneously, the rotational speed of the person increased. – We propose tentatively that when the rotational inertia I of an extended body in an isolated system decreases, its rotational speed ω increases, and vice versa. • We can test this idea with a testing experiment. © 2014 Pearson Education, Inc.

Rotational momentum © 2014 Pearson Education, Inc.

Rotational/Angular Momentum © 2014 Pearson Education, Inc.

Rotational momentum is constant for an isolated system • If a system with one rotating body is isolated, then the external torque exerted on the object is zero. • In such a case, the rotational momentum of the object does not change: 0 = Lf – Li Lf = Li © 2014 Pearson Education, Inc.

Rotational momentum is constant for an isolated system • © 2014 Pearson Education, Inc.

Rotational momentum is constant for an isolated system • © 2014 Pearson Education, Inc.

Rotational momentum The Skater Problem • The standard example used to illustrate the conservation of angular momentum is the ice skater. Start by assuming a frictionless surface - ice is pretty close to that - although if it were totally frictionless, the skater would not be able to stand up and skate! • The skater starts with his arms stretched out and spins around in place. He then pulls in his arms. • What happens to his rotational velocity after he pulls in his arms? • After you discuss this in your groups, please click on the below and see if you were correct. Why did this happen? • https: //www. youtube. com/watch? v=Mj. Yk 5 TRp. Ol. E © 2014 Pearson Education, Inc.

Rotational momentum The Skater Problem • By assuming a nearly frictionless surface, that implies there is no net external torque on the skater, so the conservation of angular momentum can be used. © 2014 Pearson Education, Inc.

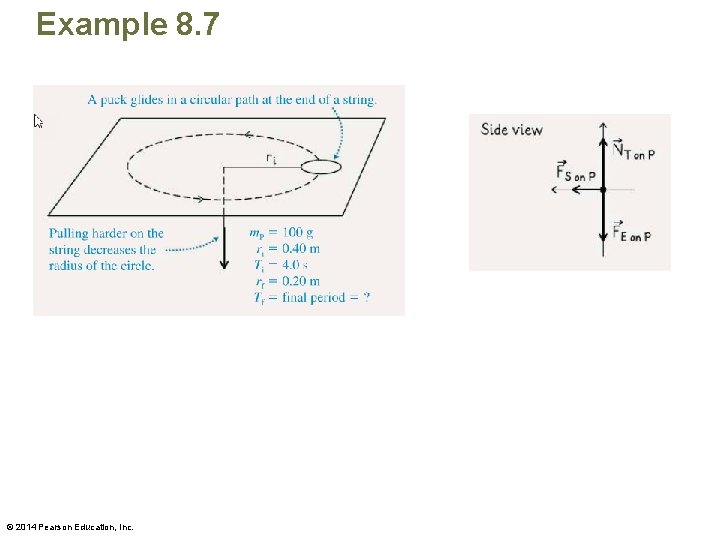
Example 8. 7 • Attach a 100 -g puck to a string, and let the puck glide in a counterclockwise circle on a horizontal, frictionless air table. The other end of the string passes through a hole at the center of the table. You pull down on the string so that the puck moves along a circular path of radius 0. 40 m. It completes one revolution in 4. 0 s. If you pull harder on the string so that the radius of the circle slowly decreases to 0. 20 m, what is the new period of revolution? © 2014 Pearson Education, Inc.

Example 8. 7 © 2014 Pearson Education, Inc.

Example 8. 7 © 2014 Pearson Education, Inc.

Example 8. 7 OK. Homework tonight. Complete the try it yourself question. Submit tomorrow. © 2014 Pearson Education, Inc.

Rotational momentum of an isolated system is constant © 2014 Pearson Education, Inc.

Example 8. 8 • Imagine that our Sun ran out of nuclear fuel and collapsed. The Sun's current period of rotation is 25 days. • What would the Sun's radius have to be for its period of rotation to be the same as during the pulsar described earlier? © 2014 Pearson Education, Inc.

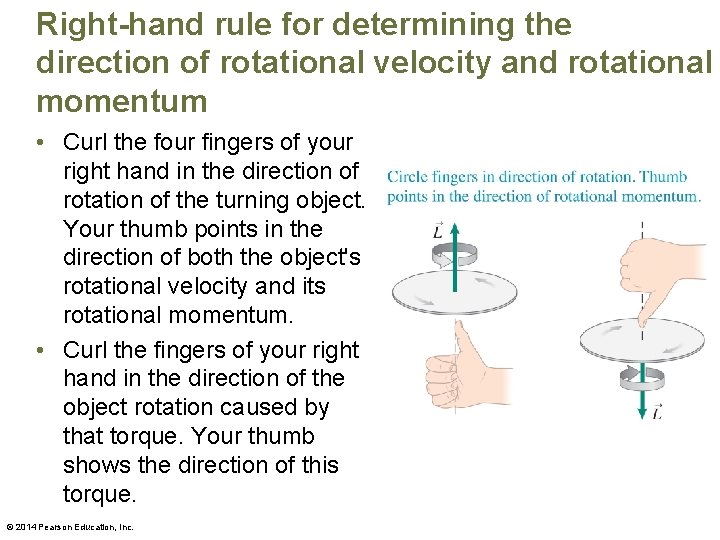
Right-hand rule for determining the direction of rotational velocity and rotational momentum • Curl the four fingers of your right hand in the direction of rotation of the turning object. Your thumb points in the direction of both the object's rotational velocity and its rotational momentum. • Curl the fingers of your right hand in the direction of the object rotation caused by that torque. Your thumb shows the direction of this torque. © 2014 Pearson Education, Inc.

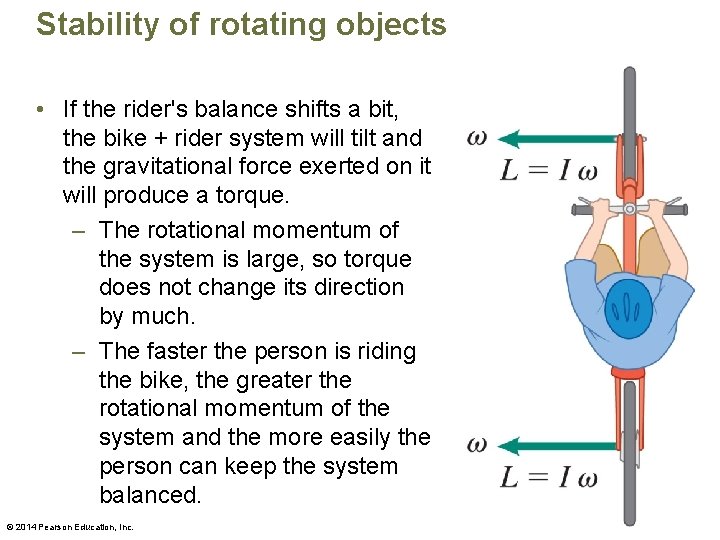
Stability of rotating objects • If the rider's balance shifts a bit, the bike + rider system will tilt and the gravitational force exerted on it will produce a torque. – The rotational momentum of the system is large, so torque does not change its direction by much. – The faster the person is riding the bike, the greater the rotational momentum of the system and the more easily the person can keep the system balanced. © 2014 Pearson Education, Inc.

8. 6 Rotational Energy © 2014 Pearson Education, Inc.

Rotational kinetic energy • We are familiar with the kinetic energy of a single particle moving along a straight line or in a circle. – It would be useful to calculate the kinetic energy of a rotating body. Doing so would allow us to use the work-energy approach to solve problems involving rotation. • We will test an analogous expression for rotational kinetic energy: © 2014 Pearson Education, Inc.

Rotational kinetic energy © 2014 Pearson Education, Inc.

Rotational kinetic energy © 2014 Pearson Education, Inc.

Rotational kinetic energy © 2014 Pearson Education, Inc.

P h y s i c s 1 D 0 3 Rolling Motion • Combined translational and rotational motion • “Rolling without slipping” • Dynamics of rolling motion

Rolling Motion • Rolling is a combination motion in which an object rotates about an axis that is moving along a straight-line trajectory. © 2015 Pearson Education, Inc.

General Motion of a Rigid Body Gives linear acceleration of the position of the center of mass. Gives angular acceleration of the body about the center of mass. Kinetic energy: These are special properties of the centre of mass only (although t = I is also true for any stationary axis of rotation). Physics 1 D 03

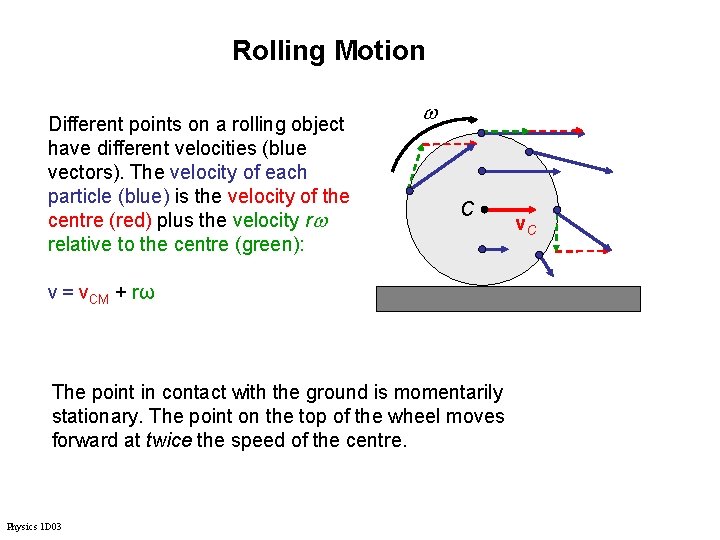
Rolling Motion Different points on a rolling object have different velocities (blue vectors). The velocity of each particle (blue) is the velocity of the centre (red) plus the velocity r relative to the centre (green): C v = v. CM + rω The point in contact with the ground is momentarily stationary. The point on the top of the wheel moves forward at twice the speed of the centre. Physics 1 D 03 v. C

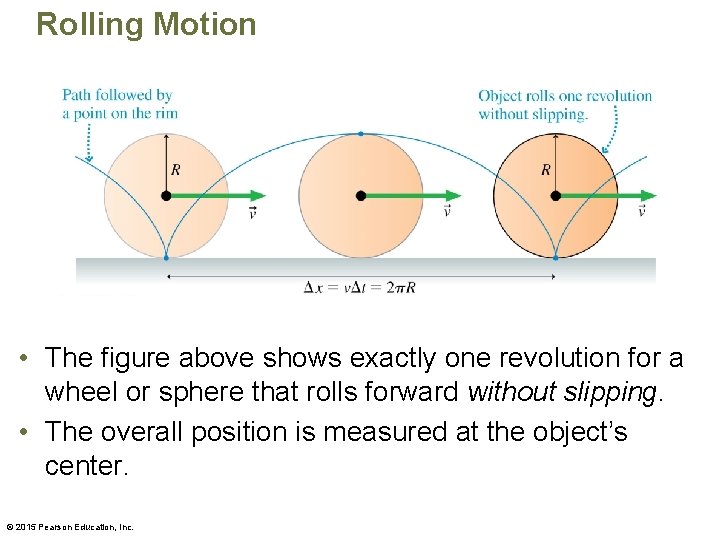
Rolling Motion • The figure above shows exactly one revolution for a wheel or sphere that rolls forward without slipping. • The overall position is measured at the object’s center. © 2015 Pearson Education, Inc.

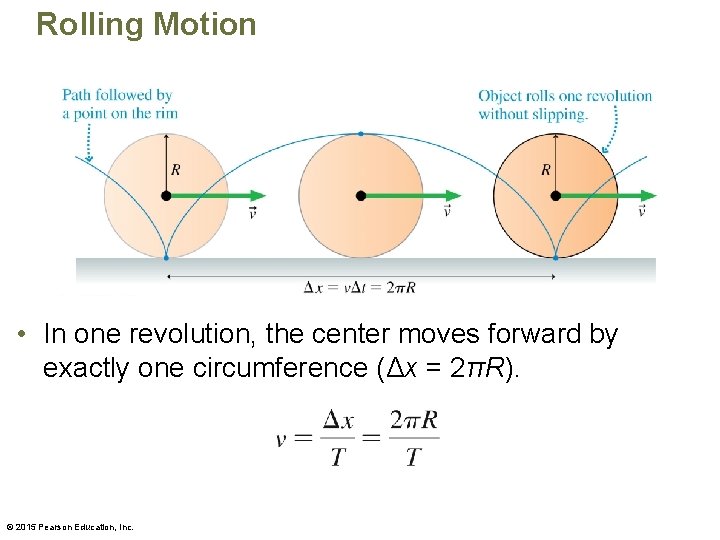
Rolling Motion • In one revolution, the center moves forward by exactly one circumference (Δx = 2πR). © 2015 Pearson Education, Inc.

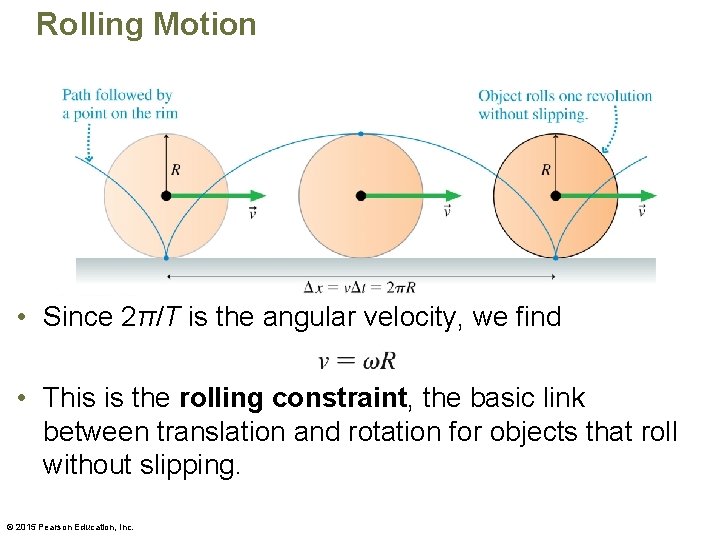
Rolling Motion • Since 2π/T is the angular velocity, we find • This is the rolling constraint, the basic link between translation and rotation for objects that roll without slipping. © 2015 Pearson Education, Inc.

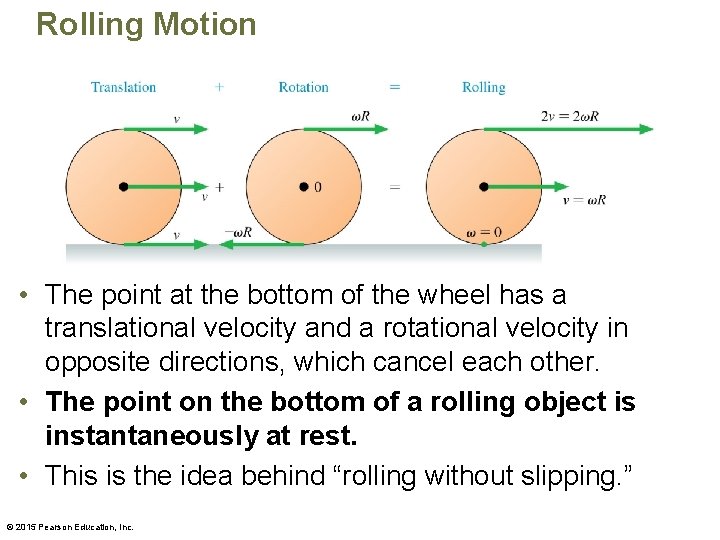
Rolling Motion • The point at the bottom of the wheel has a translational velocity and a rotational velocity in opposite directions, which cancel each other. • The point on the bottom of a rolling object is instantaneously at rest. • This is the idea behind “rolling without slipping. ” © 2015 Pearson Education, Inc.

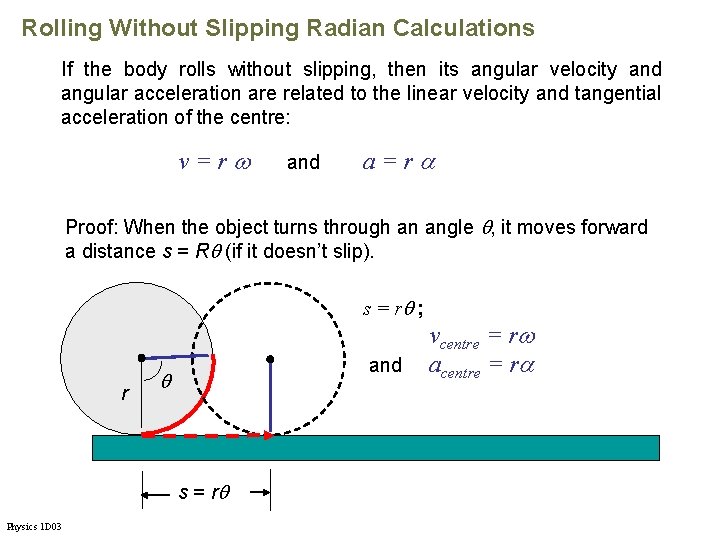
Rolling Without Slipping Radian Calculations If the body rolls without slipping, then its angular velocity and angular acceleration are related to the linear velocity and tangential acceleration of the centre: v=r and a=r Proof: When the object turns through an angle , it moves forward a distance s = R (if it doesn’t slip). s = r ; r and s = r Physics 1 D 03 vcentre = r acentre = r

Quiz There is friction between a wheel and the road, otherwise a car could not accelerate. This friction is what causes a rolling wheel to stop. a) True Physics 1 D 03 b) False

Friction and Rolling Resistance Friction is necessary to create a torque which can cause rotation and rolling. This is static friction if the wheel rolls without slipping. At the point of contact between the road and wheel, there is no relative motion, and friction does no work. pull R f “Rolling resistance” which slows the wheel results from the tire (and the road surface) flexing inelastically at the contact point. This can be a small effect, so wheels roll a long way. Physics 1 D 03

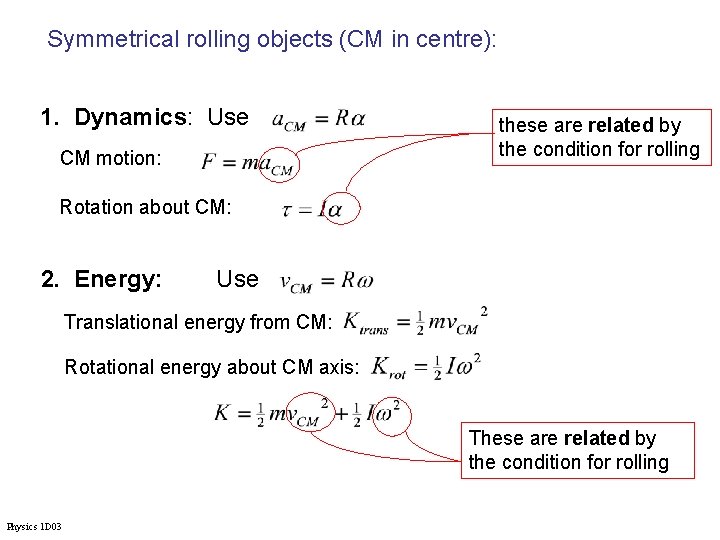
Symmetrical rolling objects (CM in centre): 1. Dynamics: Use CM motion: these are related by the condition for rolling Rotation about CM: 2. Energy: Use Translational energy from CM: Rotational energy about CM axis: These are related by the condition for rolling Physics 1 D 03

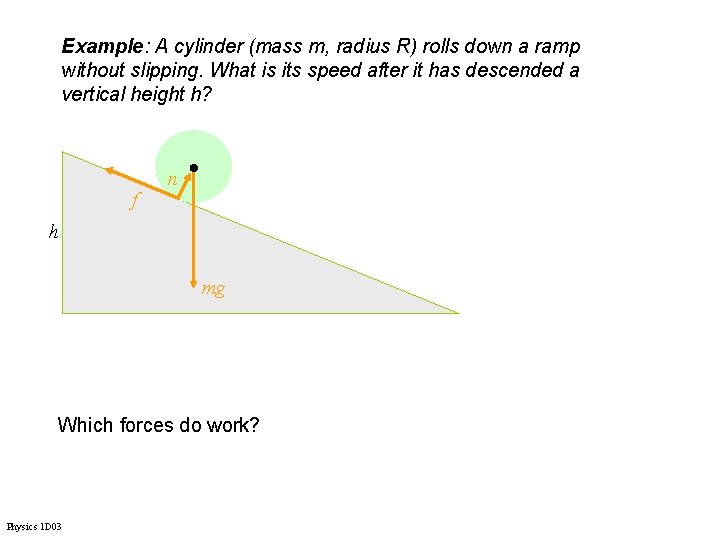
Example: A cylinder (mass m, radius R) rolls down a ramp without slipping. What is its speed after it has descended a vertical height h? f n h mg Which forces do work? Physics 1 D 03

How would you calculate the force of static friction? forces (x components): mg torques (clockwise): solve (exercise for student!). . . y f a mg Physics 1 D 03 Rf = ICM a. CM= R rolling: N sin – f = ma. CM x

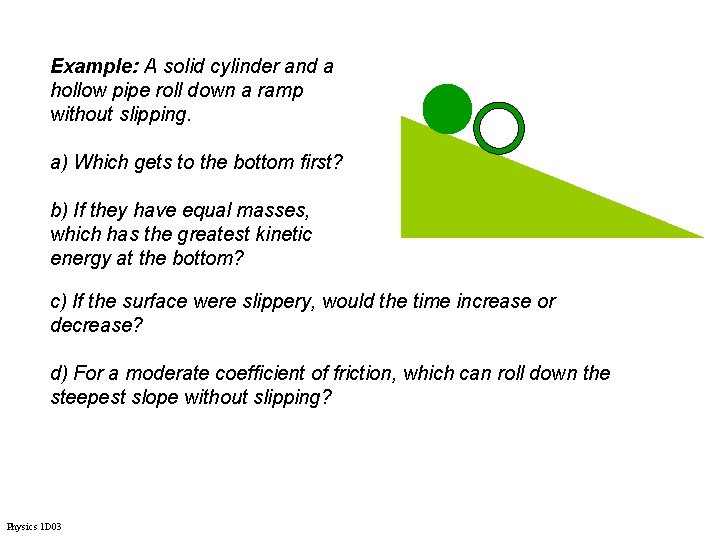
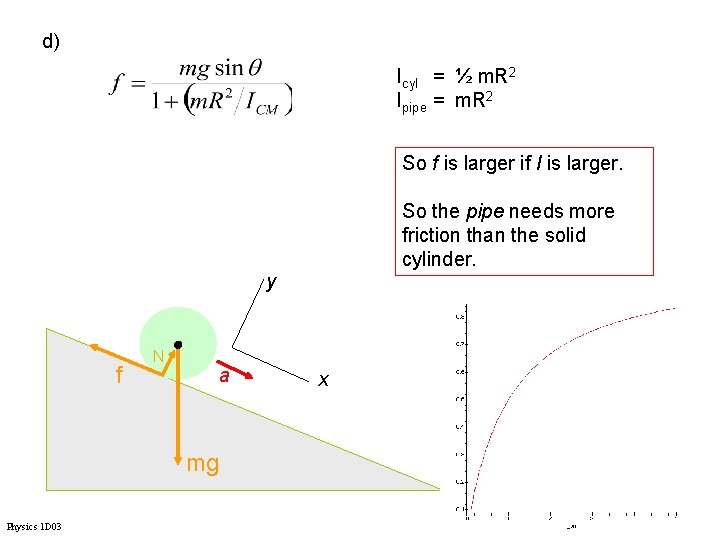
Example: A solid cylinder and a hollow pipe roll down a ramp without slipping. a) Which gets to the bottom first? b) If they have equal masses, which has the greatest kinetic energy at the bottom? c) If the surface were slippery, would the time increase or decrease? d) For a moderate coefficient of friction, which can roll down the steepest slope without slipping? Physics 1 D 03

d) Icyl = ½ m. R 2 Ipipe = m. R 2 So f is larger if I is larger. So the pipe needs more friction than the solid cylinder. y f N a mg Physics 1 D 03 x

Summary For arbitrary motion of a rigid body, divide the motion into a linear motion of the centre of mass, plus rotation about the centre of mass. Then: Rolling without slipping: Physics 1 D 03 v=R at = R

Flywheels for storing and providing energy • In a car with a flywheel, instead of rubbing a brake pad against the wheel and slowing it down, the braking system converts the car's translational kinetic energy into the rotational kinetic energy of the flywheel. • As the car's translational speed decreases, the flywheel's rotational speed increases. This rotational kinetic energy could then be used later to help the car start moving again. © 2014 Pearson Education, Inc.

Example 8. 9 • A 1600 -kg car traveling at a speed of 20 m/s approaches a stop sign. If it could transfer all of its translational kinetic energy to a 0. 20 -m-radius, 20 -kg flywheel while stopping, what rotational speed would the flywheel acquire? © 2014 Pearson Education, Inc.

Example 8. 9 © 2014 Pearson Education, Inc.

Example 8. 9 © 2014 Pearson Education, Inc.

Example 8. 9 © 2014 Pearson Education, Inc.

Rotational motion: Putting it all together—Tides and Earth's day • Point A is closer to the Moon than point B, so the gravitational force exerted by the Moon on point A is greater than that exerted on point B. – Due to the difference in forces, Earth elongates along the line connecting its center to the Moon's center. – This makes water rise to a high tide at point A and (surprisingly) at point B. The water "sags" a little at points C and D, forming low tides at those locations. © 2014 Pearson Education, Inc.

Summary © 2014 Pearson Education, Inc.

Summary © 2014 Pearson Education, Inc.

Summary © 2014 Pearson Education, Inc.

OK Lets Put It All Togheter • • • Torque and Forces and Static Equilibrium Axis of Rotation and Agular Properties Rotational Kinematics (Fab four for rotation) Rotational Dynamics (translational Force and rotational motion torque). This includes rotational inertia. • Rotational Kinetic Energy • Angular/Rotational Momentum © 2014 Pearson Education, Inc.

Questions © 2014 Pearson Education, Inc.

Example 7. 5 Finding the speed at two points on a CD The diameter of an audio compact disk is 12. 0 cm. When the disk is spinning at its maximum rate of 540 rpm, what is the speed of a point (a) at a distance 3. 0 cm from the center and (b) at the outside edge of the disk, 6. 0 cm from the center? PREPARE Consider two points A and B on the rotating compact disk in FIGURE 7. 7. During one period T, the disk rotates once, and both points rotate through the same angle, 2π rad. Thus the angular speed, ω = 2π/T, is the same for these two points; in fact, it is the same for all points on the disk. © 2015 Pearson Education, Inc.

Example 7. 5 Finding the speed at two points on a CD (cont. ) But as they go around one time, the two points move different distances. The outer point B goes around a larger circle. The two points thus have different speeds. We can solve this problem by first finding the angular speed of the disk and then computing the speeds at the two points. © 2015 Pearson Education, Inc.

Example 7. 5 Finding the speed at two points on a CD (cont. ) We first convert the frequency of the disk to rev/s: SOLVE We then compute the angular speed using Equation 7. 6: © 2015 Pearson Education, Inc.

Example 7. 5 Finding the speed at two points on a CD (cont. ) We can now use Equation 7. 7 to compute the speeds of points on the disk. At point A, r = 3. 0 cm = 0. 030 m, so the speed is At point B, r = 6. 0 cm = 0. 060 m, so the speed at the outside edge is © 2015 Pearson Education, Inc.

Example 7. 5 Finding the speed at two points on a CD (cont. ) The speeds are a few meters per second, which seems reasonable. The point farther from the center is moving at a higher speed, as we expected. ASSESS © 2015 Pearson Education, Inc.

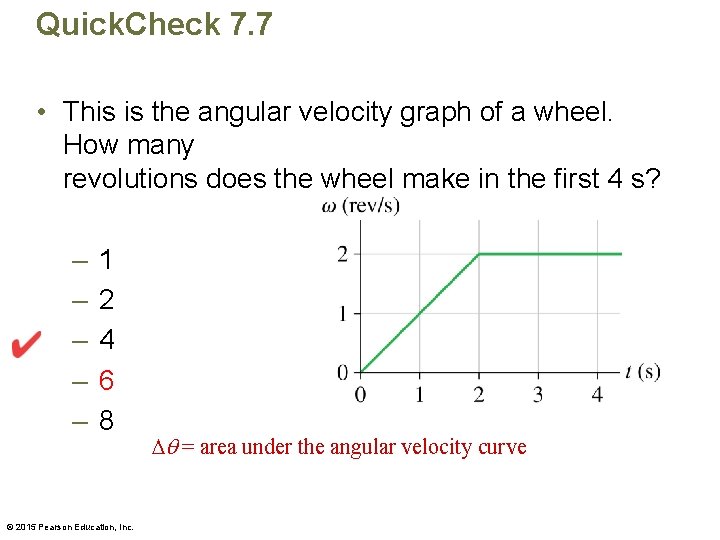
Quick. Check 7. 7 • This is the angular velocity graph of a wheel. How many revolutions does the wheel make in the first 4 s? – – – 1 2 4 6 8 © 2015 Pearson Education, Inc.

Quick. Check 7. 7 • This is the angular velocity graph of a wheel. How many revolutions does the wheel make in the first 4 s? – – – 1 2 4 6 8 © 2015 Pearson Education, Inc. = area under the angular velocity curve

Quick. Check 7. 9 • Starting from rest, a wheel with constant angular acceleration turns through an angle of 25 rad in a time t. Through what angle will it have turned after time 2 t? – – – 25 rad 50 rad 75 rad 100 rad 200 rad © 2015 Pearson Education, Inc.

Quick. Check 7. 9 • Starting from rest, a wheel with constant angular acceleration turns through an angle of 25 rad in a time t. Through what angle will it have turned after time 2 t? – – – 25 rad 50 rad 75 rad 100 rad 200 rad © 2015 Pearson Education, Inc.