Copyright 2007 Pearson Education Inc Publishing as Pearson

Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 1

Chapter 5 The Definite Integral Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall

5. 1 Estimating with Finite Sums Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall

Quick Review Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 4

Quick Review Solutions Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 5

What you’ll learn about n n Distance Traveled Rectangular Approximation Method (RAM) Volume of a Sphere Cardiac Output … and why Learning about estimating with finite sums sets the foundation for understanding integral calculus. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 6

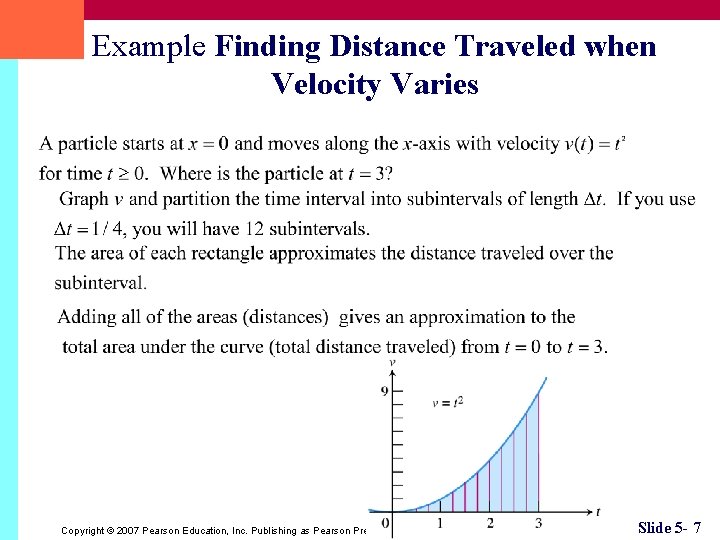
Example Finding Distance Traveled when Velocity Varies Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 7

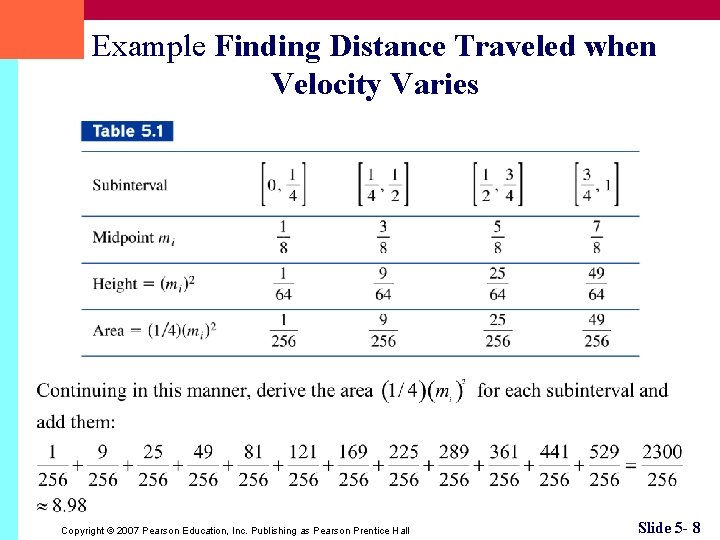
Example Finding Distance Traveled when Velocity Varies Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 8

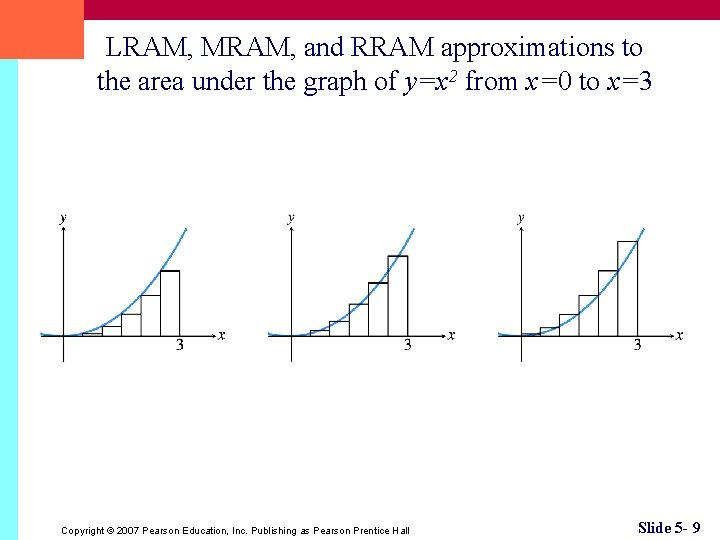
LRAM, MRAM, and RRAM approximations to the area under the graph of y=x 2 from x=0 to x=3 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 9

Example Estimating Area Under the Graph of a Nonnegative Function Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 10

5. 2 Definite Integrals Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall

Quick Review Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 12

Quick Review Solutions Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 13

What you’ll learn about n n Riemann Sums The Definite Integral Computing Definite Integrals on a Calculator Integrability … and why The definite integral is the basis of integral calculus, just as the derivative is the basis of differential calculus. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 14

Sigma Notation Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 15

The Definite Integral as a Limit of Riemann Sums Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 16

The Existence of Definite Integrals Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 17

The Definite Integral of a Continuous Function on [a, b] Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 18

The Definite Integral Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 19

Example Using the Notation Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 20

Area Under a Curve (as a Definite Integral) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 21

Area Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 22

The Integral of a Constant Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 23

Example Using NINT Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 24

5. 3 Definite Integrals and Antiderivatives Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall

Quick Review Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 26

Quick Review Solutions Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 27

What you’ll learn about n n Properties of Definite Integrals Average Value of a Function Mean Value Theorem for Definite Integrals Connecting Differential and Integral Calculus … and why Working with the properties of definite integrals helps us to understand better the definite integral. Connecting derivatives and definite integrals sets the stage for the Fundamental Theorem of Calculus. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 28

Rules for Definite Integrals Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 29

Example Using the Rules for Definite Integrals Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 30

Example Using the Rules for Definite Integrals Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 31

Example Using the Rules for Definite Integrals Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 32

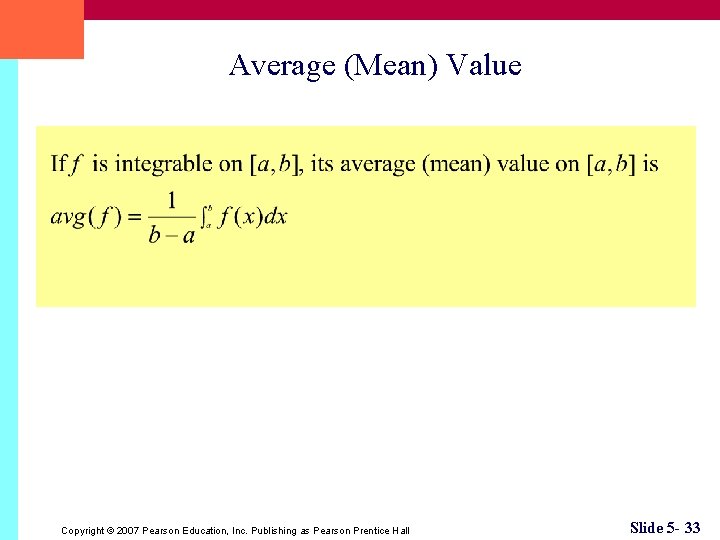
Average (Mean) Value Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 33

Example Applying the Definition Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 34

The Mean Value Theorem for Definite Integrals Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 35

The Mean Value Theorem for Definite Integrals Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 36

The Derivative of an Integral Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 37

Quick Quiz Sections 5. 1 - 5. 3 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 38

Quick Quiz Sections 5. 1 - 5. 3 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 39

Quick Quiz Sections 5. 1 - 5. 3 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 40

Quick Quiz Sections 5. 1 - 5. 3 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 41

Quick Quiz Sections 5. 1 - 5. 3 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 42

Quick Quiz Sections 5. 1 - 5. 3 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 43

5. 4 Fundamental Theorem of Calculus Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall

Quick Review Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 45

Quick Review Solutions Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 46

What you’ll learn about n n n Fundamental Theorem, Part 1 Graphing the Function Fundamental Theorem, Part 2 Area Connection Analyzing Antiderivatives Graphically … and why The Fundamental Theorem of Calculus is a Triumph of Mathematical Discovery and the key to solving many problems. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 47

The Fundamental Theorem of Calculus Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 48

The Fundamental Theorem of Calculus Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 49

Example Applying the Fundamental Theorem Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 50

Example The Fundamental Theorem with the Chain Rule Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 51

Example Variable Lower Limits of Integration Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 52

The Fundamental Theorem of Calculus, Part 2 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 53

The Fundamental Theorem of Calculus, Part 2 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 54

Example Evaluating an Integral Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 55

How to Find Total Area Analytically Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 56

How to Find Total Area Numerically Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 57

5. 5 Trapezoidal Rule Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall

Quick Review Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 59

Quick Review Solutions Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 60

What you’ll learn about n n n Trapezoidal Approximations Other Algorithms Error Analysis … and why Some definite integrals are best found by numerical approximations, and rectangles are not always the most efficient figures to use. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 61

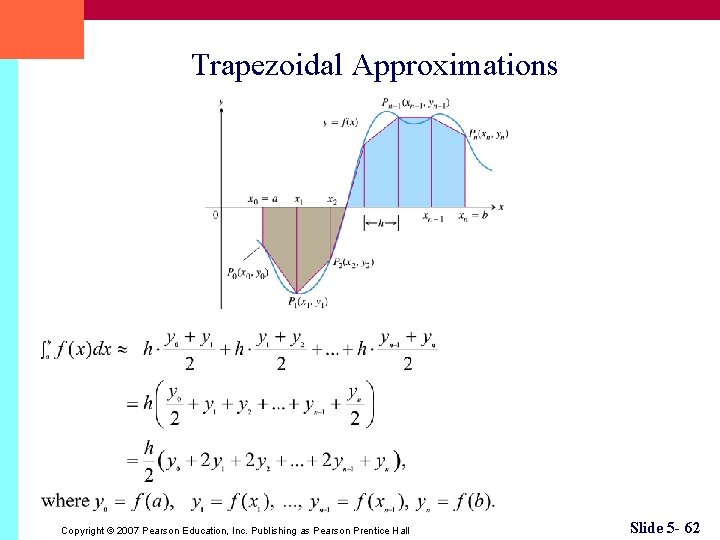
Trapezoidal Approximations Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 62

The Trapezoidal Rule Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 63

Simpson’s Rule Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 64

Error Bounds Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 65

Quick Quiz Sections 5. 4 and 5. 5 x 1 4 6 7 f(x) 10 30 40 20 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 66

Quick Quiz Sections 5. 4 and 5. 5 x 1 4 6 7 f(x) 10 30 40 20 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 67

Quick Quiz Sections 5. 4 and 5. 5 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 68

Quick Quiz Sections 5. 4 and 5. 5 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 69

Quick Quiz Sections 5. 4 and 5. 5 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 70

Quick Quiz Sections 5. 4 and 5. 5 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 71

Chapter Test Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 72

Chapter Test Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 73

Chapter Test 8. A diesel generator runs continuously, consuming oil at a gradually increasing rate until it must be temporarily shut down to have the filters replaced. (a) Give an upper estimate and a lower estimate for the amount of oil consumed by the generator during that week. (b) Use the Trapezoidal Rule to estimate the amount of oil consumed by the generator during that week. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 74

Chapter Test Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 75

Chapter Test Solutions Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 76

Chapter Test Solutions Let R be the region in the first quadrant enclosed by the x-axis and the graph of the function y = 4 x – x. 1. Sketch the rectangles and compute by hand the area for the MRAM 3 4 approximations. 4. 125 2. Sketch the trapeziods and compute by hand the area for the T 4 approximations. 3. 75 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 77

Chapter Test Solutions Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 78

Chapter Test Solutions 8. A diesel generator runs continuously, consuming oil at a gradually increasing rate until it must be temporarily shut down to have the filters replaced. (a) Give an upper estimate and a lower estimate for the amount of oil consumed by the generator during that week. Upper = 4. 392 L; Lower = 4. 008 L (b) Use the Trapezoidal Rule to estimate the amount of oil consumed by the generator during that week. 4. 2 L Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 79

Chapter Test Solutions Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 5 - 80