2011 Pearson Education Inc Statistics for Business and

Statistics for Business and Economics Chapter 5 Inferences Based on a Single Sample: Estimation

Content 1. Identifying and Estimating the Target Parameter 2. Confidence Interval for a Population Mean: Normal (z) Statistic 3. Confidence Interval for a Population Mean: Student’s t-Statistic 4. Large-Sample Confidence Interval for a Population Proportion 5. Determining the Sample Size 6. Finite Population Correction for Simple Random Sampling 7. Sample Survey Designs © 2011 Pearson Education, Inc

Learning Objectives 1. Estimate a population parameter (means or proportion) based on a large sample selected from the population 2. Use the sampling distribution of a statistic to form a confidence interval for the population parameter 3. Show to select the proper sample size for estimating a population parameter © 2011 Pearson Education, Inc

Thinking Challenge Suppose you’re interested in the average amount of money that students in

Statistical Methods Descriptive Statistics Inferential Statistics Estimation © 2011 Pearson Education, Inc Hypothesis Testing

5. 1 Identifying and Estimating the Target Parameter © 2011 Pearson Education, Inc

Estimation Methods Estimation Point Estimation Interval Estimation © 2011 Pearson Education, Inc

Target Parameter The unknown population parameter (e. g. , mean or proportion) that we

Target Parameter Determining the Target Parameter Key Words of Phrase Type of Data µ

Point Estimator A point estimator of a population parameter is a rule or formula that tells us how to use the sample data to calculate a single number that can be used as an estimate of the target parameter. © 2011 Pearson Education, Inc

Point Estimation 1. Provides a single value • Based on observations from one sample 2. Gives no information about how close the value is to the unknown population parameter 3. Example: Sample mean x = 3 is the point estimate of the unknown population mean © 2011 Pearson Education, Inc

Interval Estimator An interval estimator (or confidence interval) is a formula that tells us how to use the sample data to calculate an interval that estimates the target parameter. © 2011 Pearson Education, Inc

Interval Estimation 1. Provides a range of values • Based on observations from one sample 2. Gives information about closeness to unknown population parameter • Stated in terms of probability – Knowing exact closeness requires knowing unknown population parameter 3. Example: Unknown population mean lies between 50 and 70 with 95% confidence © 2011 Pearson Education, Inc

5. 2 Confidence Interval for a Population Mean: Normal (z) Statistic © 2011 Pearson

Estimation Process Population Mean, , is unknown Random Sample Mean x = 50 Sample

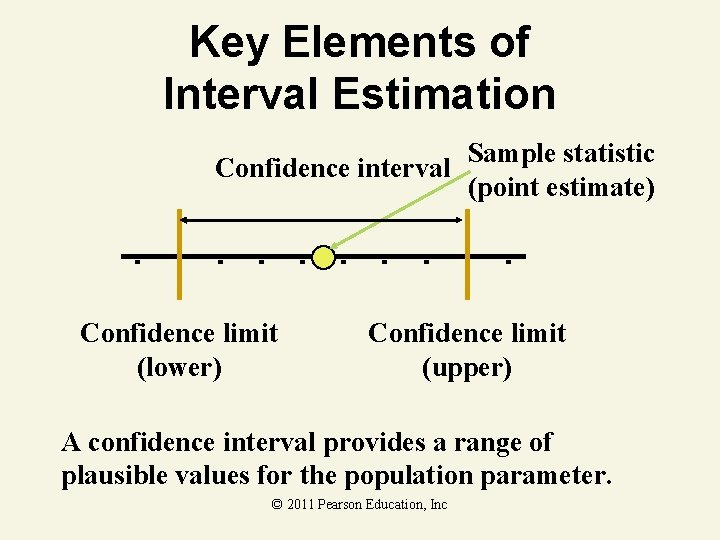
Key Elements of Interval Estimation Sample statistic Confidence interval (point estimate) Confidence limit (lower) Confidence limit (upper) A confidence interval provides a range of plausible values for the population parameter. © 2011 Pearson Education, Inc

Confidence Interval According to the Central Limit Theorem, the sampling distribution of the sample mean is approximately normal for large samples. Let us calculate the interval estimator: That is, we form an interval from 1. 96 standard deviations below the sample mean to 1. 96 standard deviations above the mean. Prior to drawing the sample, what are the chances that this interval will enclose µ, the population mean? © 2011 Pearson Education, Inc

Confidence Interval If sample measurements yield a value of that falls between the two lines on either side of µ, then the interval will contain µ. The area under the normal curve between these two boundaries is exactly. 95. Thus, the probability that a randomly selected interval will contain µ is equal to. 95. © 2011 Pearson Education, Inc

Confidence Coefficient The confidence coefficient is the probability that a randomly selected confidence interval encloses the population parameter - that is, the relative frequency with which similarly constructed intervals enclose the population parameter when the estimator is used repeatedly a very large number of times. The confidence level is the confidence coefficient expressed as a percentage. © 2011 Pearson Education, Inc

95% Confidence Level If our confidence level is 95%, then in the long run, 95% of our confidence intervals will contain µ and 5% will not. For a confidence coefficient of 95%, the area in the two tails is. 05. To choose a different confidence coefficient we increase or decrease the area (call it ) assigned to the tails. If we place /2 in each tail and z /2 is the z-value, the confidence interval with coefficient (1 – ) is © 2011 Pearson Education, Inc

Conditions Required for a Valid Large-Sample Confidence Interval for µ 1. A random sample is selected from the target population. 2. The sample size n is large (i. e. , n ≥ 30). Due to the Central Limit Theorem, this condition guarantees that the sampling distribution of is approximately normal. Also, for large n, s will be a good estimator of . © 2011 Pearson Education, Inc

Large-Sample (1 – )% Confidence Interval for µ where z /2 is the z-value with an area /2 to its right and The parameter is the standard deviation of the sampled population, and n is the sample size. Note: When is unknown and n is large (n ≥ 30), the confidence interval is approximately equal to where s is the sample standard deviation. © 2011 Pearson Education, Inc

Thinking Challenge You’re a Q/C inspector for Gallo. The for 2 -liter bottles is. 05 liters. A random sample of 100 bottles showed x = 1. 99 liters. What is the 90% confidence interval estimate of the true mean amount in 2 -liter bottles? 22 liter © 2011 Pearson Education, Inc © 1984 -1994 T/Maker Co.

Confidence Interval Solution* © 2011 Pearson Education, Inc

5. 3 Confidence Interval for a Population Mean: Student’s t-Statistic © 2011 Pearson Education,

Small Sample Unknown Instead of using the standard normal statistic use the t–statistic in which the sample standard deviation, s, replaces the population standard deviation, . © 2011 Pearson Education, Inc

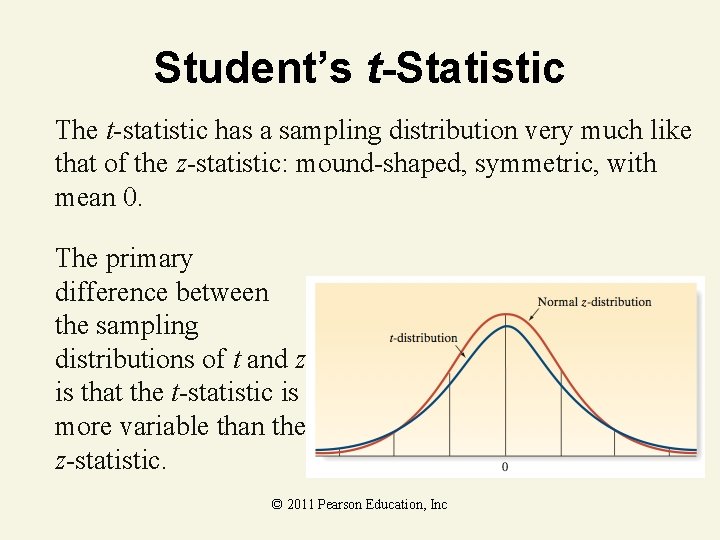
Student’s t-Statistic The t-statistic has a sampling distribution very much like that of the z-statistic: mound-shaped, symmetric, with mean 0. The primary difference between the sampling distributions of t and z is that the t-statistic is more variable than the z-statistic. © 2011 Pearson Education, Inc

Degrees of Freedom The actual amount of variability in the sampling distribution of t depends on the sample size n. A convenient way of expressing this dependence is to say that the t-statistic has (n – 1) degrees of freedom (df). © 2011 Pearson Education, Inc

Student’s t Distribution Standard Normal Bell-Shaped t (df = 13) Symmetric t (df =

t-value If we want the t-value with an area of. 025 to its right and 4 df, we look in the table under the column t. 025 for the entry in the row corresponding to 4 df. This entry is t. 025 = 2. 776. The corresponding standard normal z-score is z. 025 = 1. 96. © 2011 Pearson Education, Inc

Small-Sample Confidence Interval for µ where ta/2 is based on (n – 1) degrees

Conditions Required for a Valid Small-Sample Confidence Interval for µ 1. A random sample is selected from the target population. 2. The population has a relative frequency distribution that is approximately normal. © 2011 Pearson Education, Inc

Estimation Example Mean ( Unknown) A random sample of n = 25 has =

Thinking Challenge You’re a time study analyst in manufacturing. You’ve recorded the following task times (min. ): 3. 6, 4. 2, 4. 0, 3. 5, 3. 8, 3. 1. What is the 90% confidence interval estimate of the population mean task time? © 2011 Pearson Education, Inc

Confidence Interval Solution* • x = 3. 7 • s = 3. 8987 •

5. 4 Large-Sample Confidence Interval for a Population Proportion © 2011 Pearson Education, Inc

Sampling Distribution of 1. The mean of the sampling distribution of is, is an unbiased estimator of p. is p; that 2. The standard deviation of the sampling distribution of is ; that is, , where q = 1–p. 3. For large samples, the sampling distribution of is approximately normal. A sample size is considered large if both © 2011 Pearson Education, Inc

Large-Sample Confidence Interval for where Note: When n is large, can approximate the value

Conditions Required for a Valid Large-Sample Confidence Interval for p 1. A random sample is selected from the target population. 2. The sample size n is large. (This condition will be satisfied if both. Note that and are simply the number of successes and number of failures, respectively, in the sample. ). © 2011 Pearson Education, Inc

Estimation Example Proportion A random sample of 400 graduates showed 32 went to graduate

Thinking Challenge You’re a production manager for a newspaper. You want to find the % defective. Of 200 newspapers, 35 had defects. What is the 90% confidence interval estimate of the population proportion defective? © 2011 Pearson Education, Inc

Adjusted (1 – )100% Confidence Interval for a Population Proportion, p where is the adjusted sample proportion of observations with the characteristic of interest, x is the number of successes in the sample, and n is the sample size. © 2011 Pearson Education, Inc

5. 5 Determining the Sample Size © 2011 Pearson Education, Inc

Sampling Error In general, we express the reliability associated with a confidence interval for the population mean µ by specifying the sampling error within which we want to estimate µ with 100(1 – �)% confidence. The sampling error (denoted SE), then, is equal to the half-width of the confidence interval. © 2011 Pearson Education, Inc

Sample Size Determination for 100(1 – ) % Confidence Interval for µ In order to estimate µ with a sampling error (SE) and with 100(1 – )% confidence, the required sample size is found as follows: The solution for n is given by the equation © 2011 Pearson Education, Inc

Sample Size Example What sample size is needed to be 90% confident the mean

Sample Size Determination for 100(1 – ) % Confidence Interval for p In order to estimate p with a sampling error SE and with 100(1 – )% confidence, the required sample size is found by solving the following equation for n: The solution for n can be written as follows: Inc Note: Always round©n 2011 up. Pearson to Education, the nearest integer value.

Sample Size Example What sample size is needed to estimate p within. 03 with

Thinking Challenge You work in Human Resources at Merrill Lynch. You plan to survey employees to find their average medical expenses. You want to be 95% confident that the sample mean is within ± $50. A pilot study showed that was about $400. What sample size do you use? © 2011 Pearson Education, Inc

Sample Size Solution* © 2011 Pearson Education, Inc

5. 6 Finite Population Correction for Simple Random Sample © 2011 Pearson Education, Inc

Finite Population Correction Factor In some sampling situations, the sample size n may represent 5% or perhaps 10% of the total number N of sampling units in the population. When the sample size is large relative to the number of measurements in the population (see the next slide), the standard errors of the estimators of µ and p should be multiplied by a finite population correction factor. © 2011 Pearson Education, Inc

Rule of Thumb for Finite Population Correction Factor Use the finite population correction factor

Simple Random Sampling with Finite Population of Size N Estimation of the Population Mean

Simple Random Sampling with Finite Population of Size N Estimation of the Population Proportion

Finite Population Correction Factor Example You want to estimate a population mean, μ, where x =115, s =18, N =700, and n = 60. Find an approximate 95% confidence interval for μ. Since is greater than. 05 use the finite correction factor © 2011 Pearson Education, Inc

Finite Population Correction Factor Example You want to estimate a population mean, μ, where x =115, s =18, N =700, and n = 60. Find an approximate 95% confidence interval for μ. © 2011 Pearson Education, Inc

5. 7 Sample Survey Designs © 2011 Pearson Education, Inc

Simple Random Sample If n elements are selected from a population in such a way that every set of n elements in the population has an equal probability of being selected, the n elements are said to be a simple random sample. © 2011 Pearson Education, Inc

Stratified Random Sampling Stratified random sampling is used when the sampling units (i. e. , the units that are sampled) associated with the population can be physically separated into two or more groups of sampling units (called strata) where the within-stratum response variation is less than the variation within the entire population. © 2011 Pearson Education, Inc

Systematic Sample Sometimes it is difficult or too costly to select random samples. For example, it would be easier to obtain a sample of student opinions at a large university by systematically selecting every hundredth name from the student directory. This type of sample design is called a systematic sample. Although systematic samples are usually easier to select than other types of samples, one difficulty is the possibility of a systematic sampling bias. © 2011 Pearson Education, Inc

Randomized Response Sampling Randomized response sampling is particularly useful when the questions of the pollsters are likely to elicit false answers. One method of coping with the false responses produced by sensitive questions is randomized response sampling. Each person is presented two questions; one question is the object of the survey, and the other is an innocuous question to which the interviewee will give an honest answer. © 2011 Pearson Education, Inc

Key Ideas Population Parameters, Estimators, and Standard Errors Parameter Estimator Standard Error of Estimator

Key Ideas Population Parameters, Estimators, and Standard Errors Confidence Interval: An interval that encloses an unknown population parameter with a certain level of confidence (1 – ) Confidence Coefficient: The probability (1 – ) that a randomly selected confidence interval encloses the true value of the population parameter. © 2011 Pearson Education, Inc

Key Ideas Key Words for Identifying the Target Parameter µ – Mean, Average p

Key Ideas Sample Survey Designs 1. Simple random sampling 2. Stratified random sampling 3.

Key Ideas Commonly Used z-Values for a Large-Sample Confidence Interval 90% CI: (1 – ) =. 10 z. 05 = 1. 645 95% CI: (1 – ) =. 05 z. 025 = 1. 96 99% CI: (1 – ) =. 01 z. 005 = 2. 575 © 2011 Pearson Education, Inc