Rotational Motion AP Physics C Rotation of Rigid

Rotational Motion AP Physics C

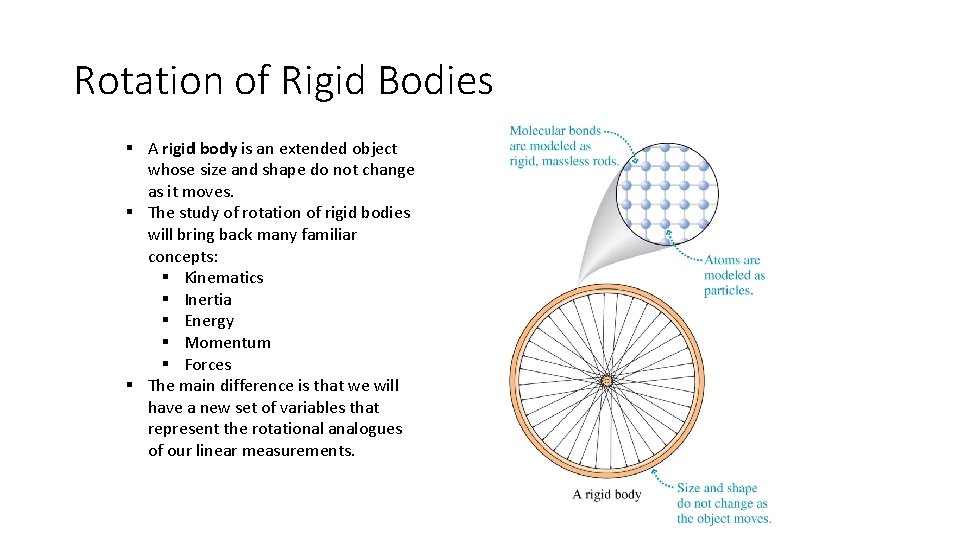
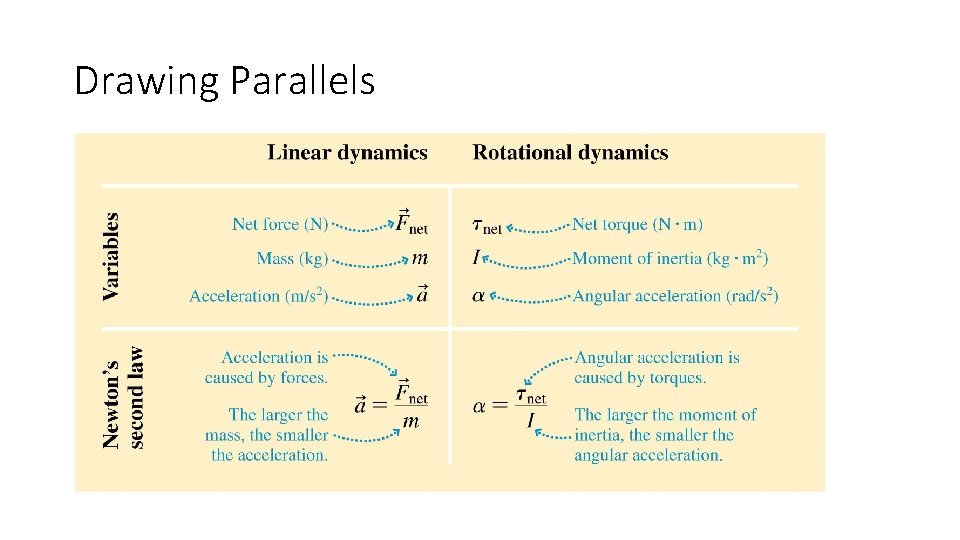
Rotation of Rigid Bodies § A rigid body is an extended object whose size and shape do not change as it moves. § The study of rotation of rigid bodies will bring back many familiar concepts: § Kinematics § Inertia § Energy § Momentum § Forces § The main difference is that we will have a new set of variables that represent the rotational analogues of our linear measurements.

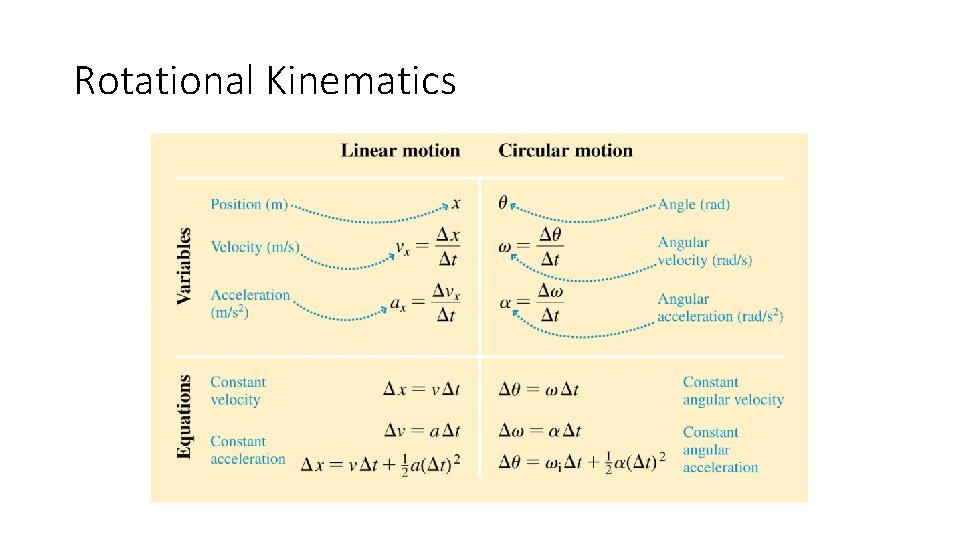
Rotational Kinematics

Angular Position, Velocity, and Acceleration § We use the angle θ from the positive x-axis to describe the particle’s location. § Angle θ is the angular position of the particle. § θ is positive (by convention) when measured counterclockwise from the positive x-axis. § We measure angle θ in the angular unit of radians, not degrees. § The unit for angular velocity is rad/s, and angular acceleration is rad/s 2.

Rotational Kinematics

Example A high-speed drill rotating counterclockwise takes 2. 5 s to speed up to 2400 rpm. What is the drill’s angular acceleration? How many revolutions does it make as it reaches top speed?

Example The angular velocity of a flywheel is given by the equation below. Calculate the angular acceleration of the flywheel at t = 3 s. Calculate the number of revolutions the flywheel goes through in the first 8 s.

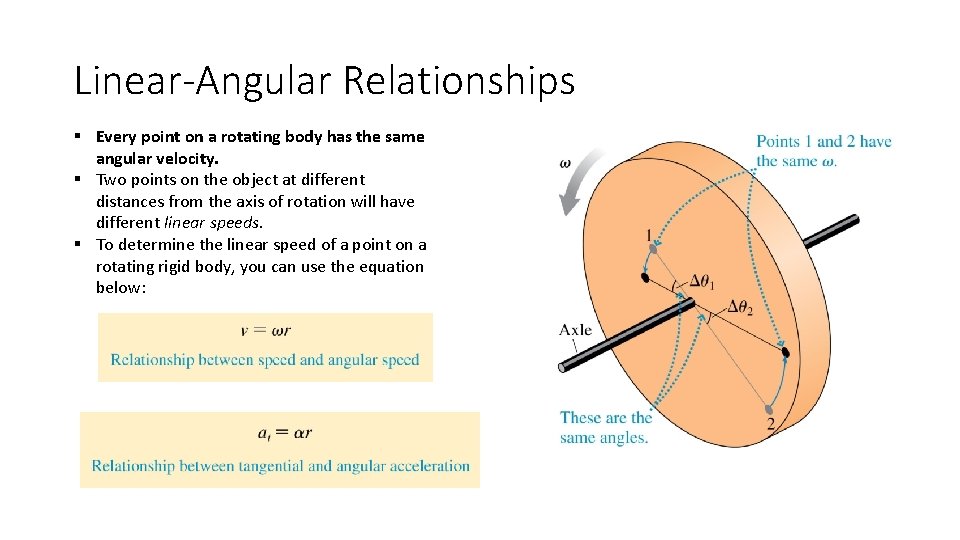
Linear-Angular Relationships § Every point on a rotating body has the same angular velocity. § Two points on the object at different distances from the axis of rotation will have different linear speeds. § To determine the linear speed of a point on a rotating rigid body, you can use the equation below:

Moment of Inertia

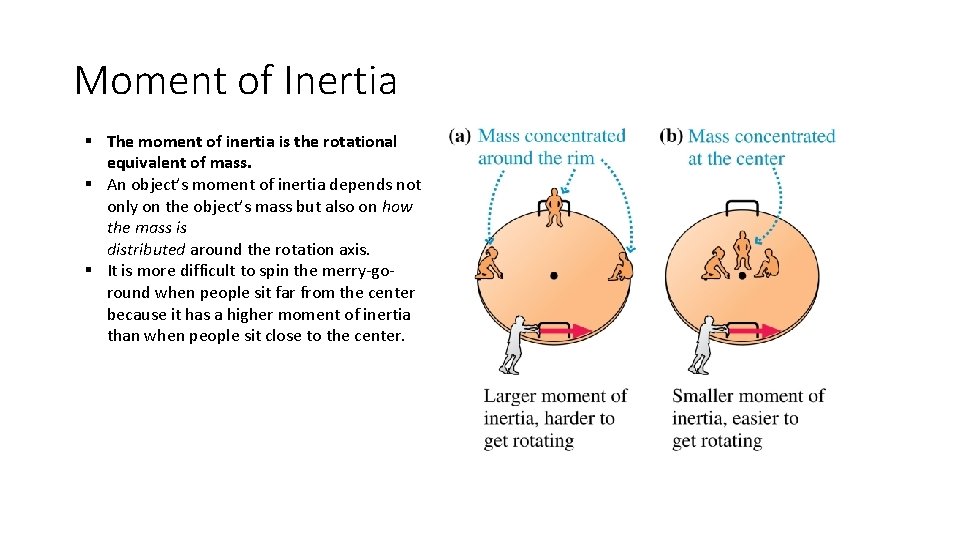
Moment of Inertia § The moment of inertia is the rotational equivalent of mass. § An object’s moment of inertia depends not only on the object’s mass but also on how the mass is distributed around the rotation axis. § It is more difficult to spin the merry-goround when people sit far from the center because it has a higher moment of inertia than when people sit close to the center.

Moment of Inertia – Point Mass § If you have rotating point masses, the moment of inertia is given by the following equation: § If you have a collection of point masses that are all rotating about a common axis, the moment of inertia of the system is the sum of the moments of all the parts of the system.

Moment of Inertia – Mass Distribution § The summation equation for moment of inertia worked fine for a collection of point masses, but what about more continuous masses like disks, rods, or sphere where the mass is extended over a volume or area? In this case, calculus is needed. § This suggests that we will take small discrete amounts of mass and add them up over a set of limits. Indeed, that is what we will do. Let’s look at a few example we “MIGHT” encounter. Consider a solid rotating about its CM.

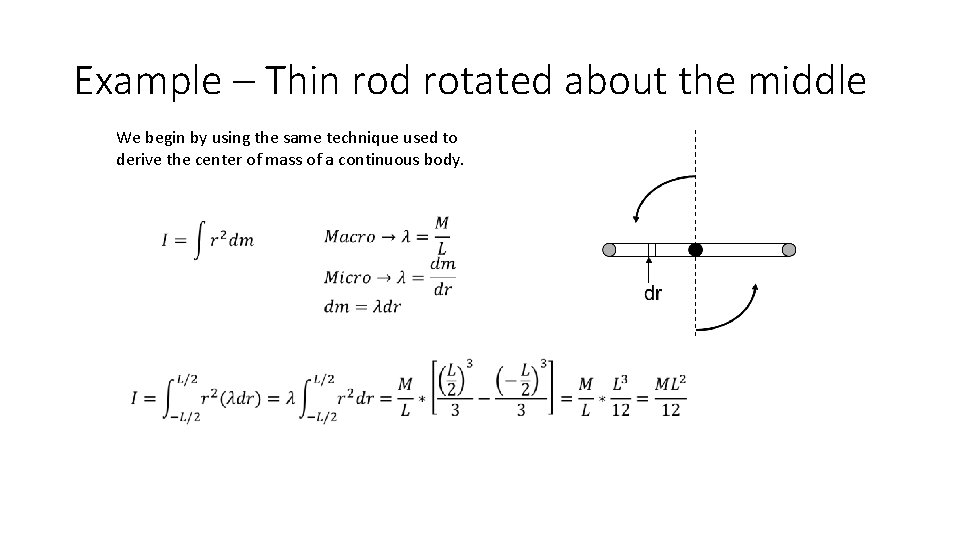
Example – Thin rod rotated about the middle We begin by using the same technique used to derive the center of mass of a continuous body.

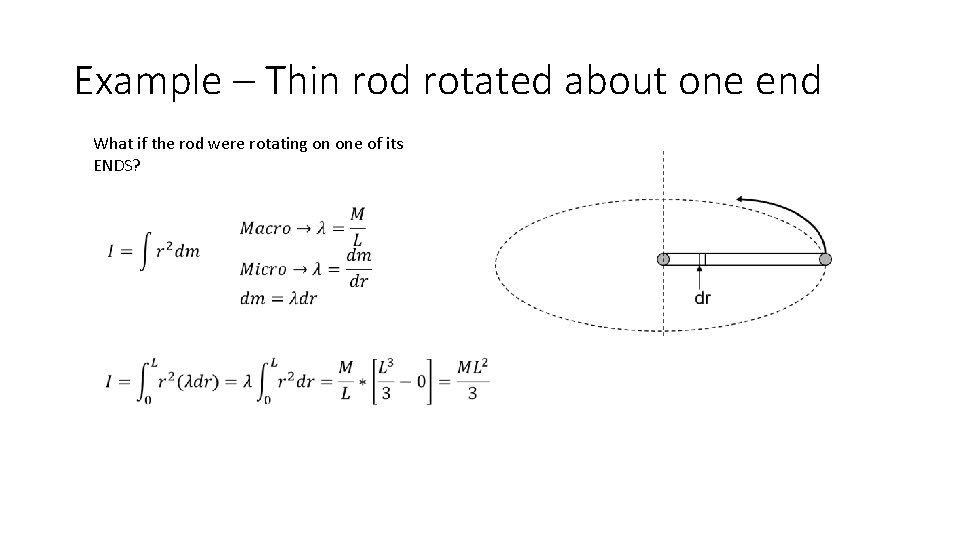
Example – Thin rod rotated about one end What if the rod were rotating on one of its ENDS?

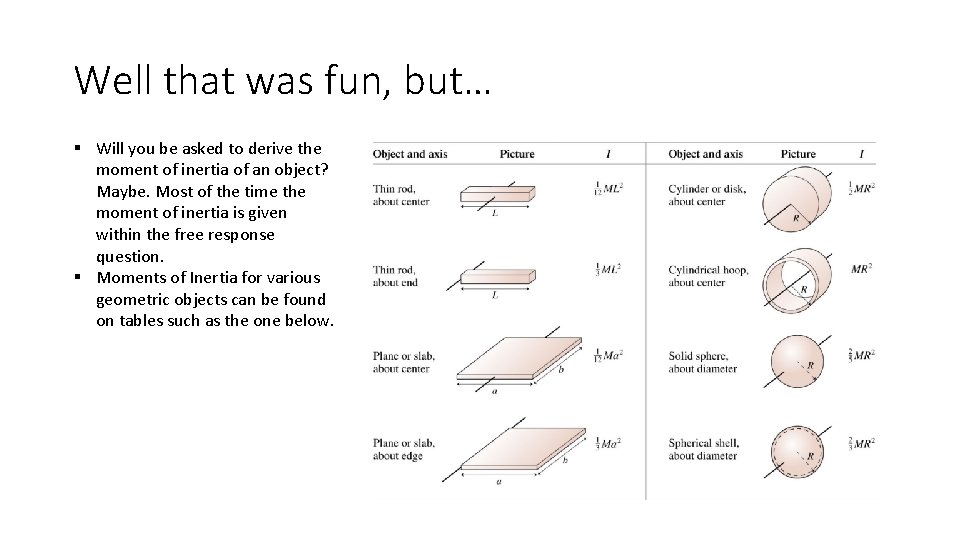
Well that was fun, but… § Will you be asked to derive the moment of inertia of an object? Maybe. Most of the time the moment of inertia is given within the free response question. § Moments of Inertia for various geometric objects can be found on tables such as the one below.

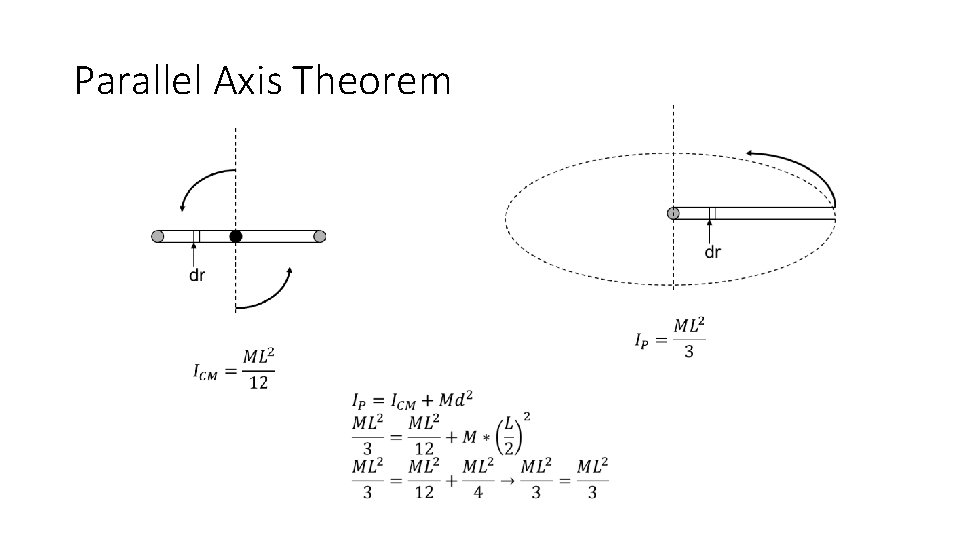
Parallel Axis Theorem This theorem will allow us to calculate the moment of inertia of any rotating body around any axis, provided we know the moment of inertia about the center of mass. It basically states that the Moment of Inertia (Ip) around any axis "P" is equal to the known moment of inertia (Icm) about some center of mass plus M (the total mass of the system) times the square of "d" (the distance between the two parallel axes) Let’s use thin rod example to prove this.

Parallel Axis Theorem

Moment of Inertia of Compound Objects § If you have two geometric objects attached to each other, you can find the moment of inertia of the system by adding the moment of inertia of the two objects (assuming they rotate about the same point). § This means that moment of inertia obeys the principle of superposition. § Notice that if the sphere is very small (L>>R), then the sphere can be approximated as a point mass, making the moment of inertia of this system:

Torque

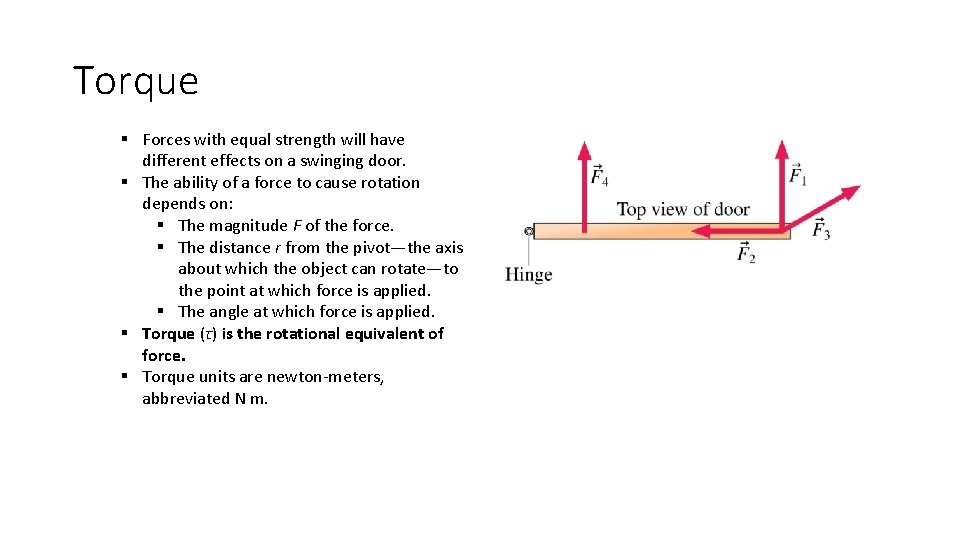
Torque § Forces with equal strength will have different effects on a swinging door. § The ability of a force to cause rotation depends on: § The magnitude F of the force. § The distance r from the pivot—the axis about which the object can rotate—to the point at which force is applied. § The angle at which force is applied. § Torque (τ) is the rotational equivalent of force. § Torque units are newton-meters, abbreviated N m.

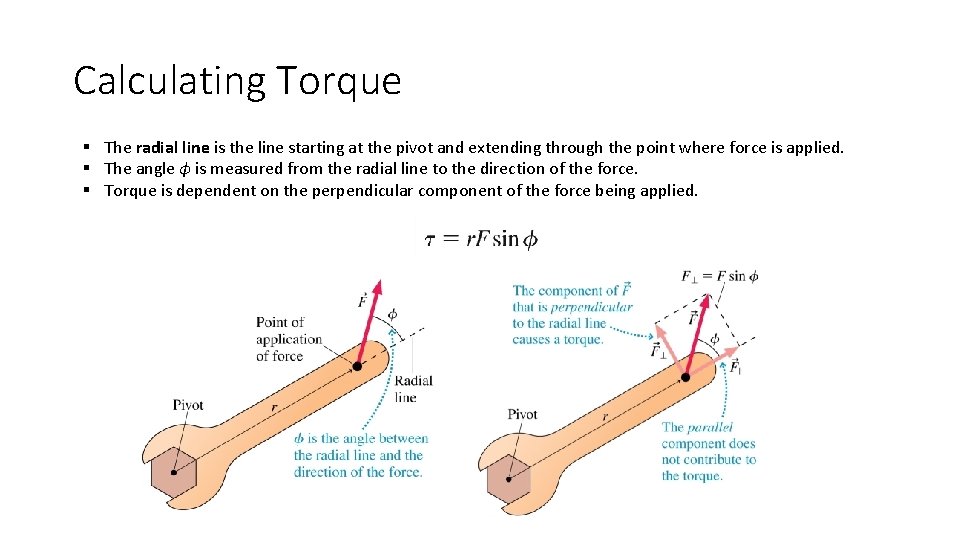
Calculating Torque § The radial line is the line starting at the pivot and extending through the point where force is applied. § The angle ϕ is measured from the radial line to the direction of the force. § Torque is dependent on the perpendicular component of the force being applied.

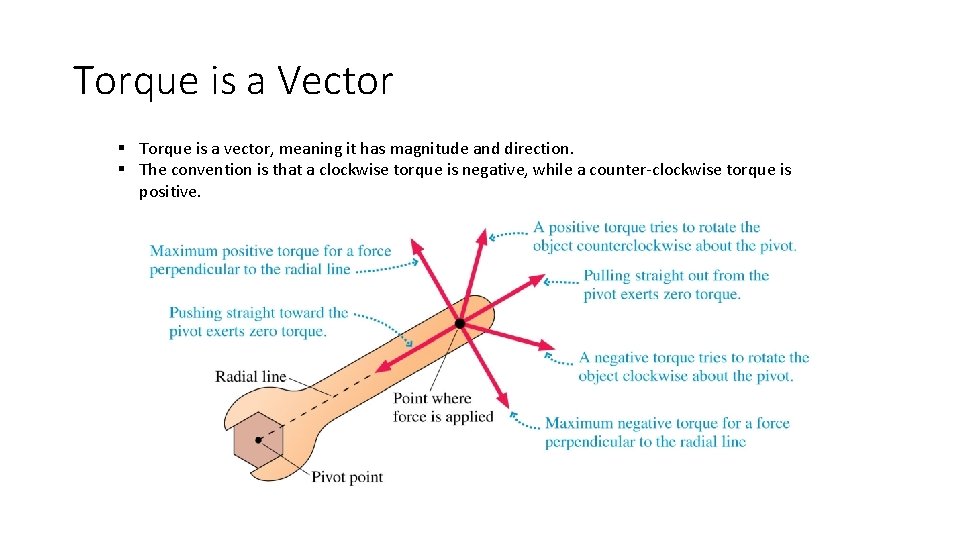
Torque is a Vector § Torque is a vector, meaning it has magnitude and direction. § The convention is that a clockwise torque is negative, while a counter-clockwise torque is positive.

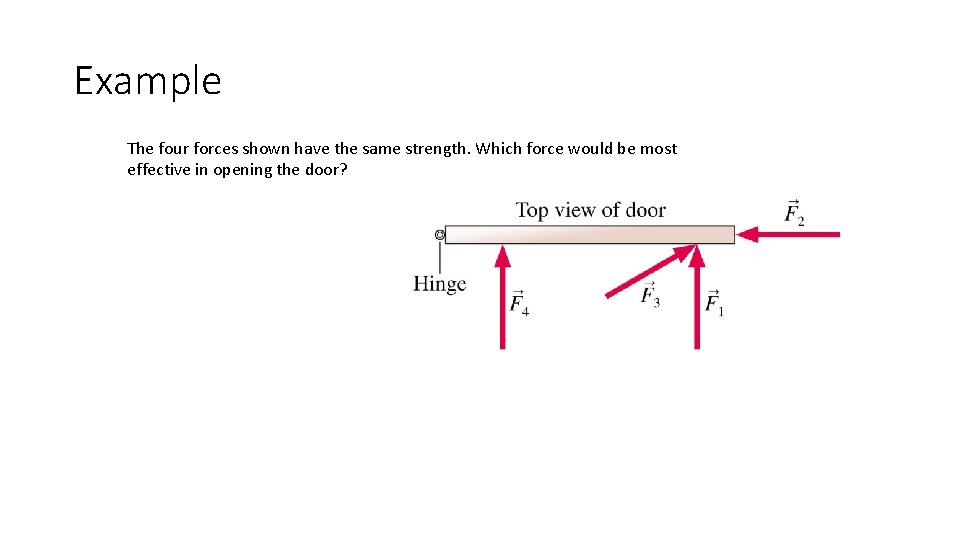
Example The four forces shown have the same strength. Which force would be most effective in opening the door?

Example Revolutionaries attempt to pull down a statue of the Great Leader by pulling on a rope tied to the top of its head. The statue is 17 m tall, and they pull with a force of 4200 N at an angle of 65° to the horizontal. What is the torque they exert on the statue?

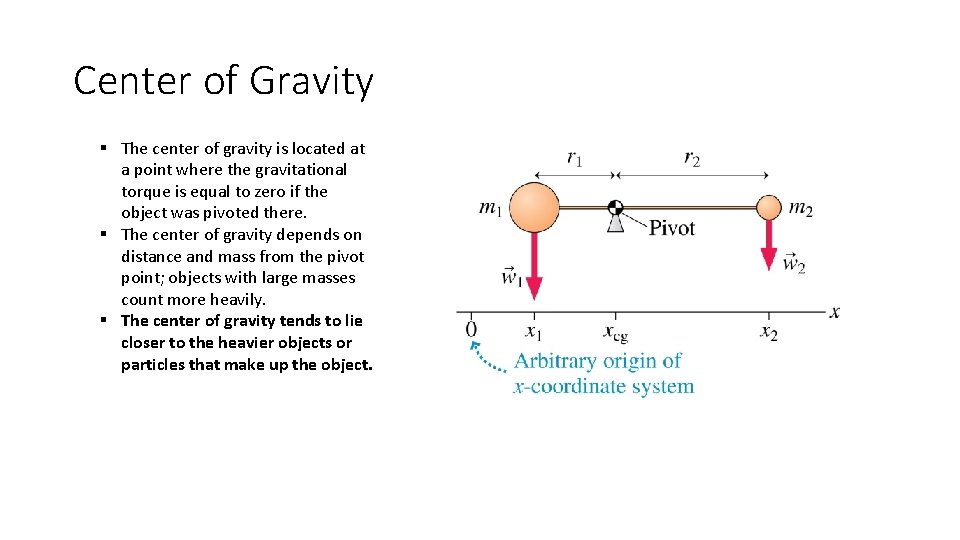
Gravitational Torque and Center of Gravity § Gravity pulls downward on every particle that makes up an object (like the gymnast). § Each particle experiences a torque due to the force of gravity. § The gravitational torque can be calculated by assuming that the net force of gravity (the object’s weight) acts as a single point. § That single point is called the center of gravity (or center of mass). § We will always consider the force of gravity to act only at the center of gravity.

Center of Gravity § The center of gravity is located at a point where the gravitational torque is equal to zero if the object was pivoted there. § The center of gravity depends on distance and mass from the pivot point; objects with large masses count more heavily. § The center of gravity tends to lie closer to the heavier objects or particles that make up the object.

Static Equilibrium § Often we will have more than one torques acting on an object. § In this case we can add these torques together (BE CAREFULL WITH DIRECTION!) to find our net torque. § If an object is at rest we can say that our net torque is equal to zero, meaning that all of our torques balance each other out. § Keep in mind that not every force exerts a torque! If a force does not provide a torque then it is not included in calculating net torque. § Forces that do not provide torques are still included when calculating net FORCE.

Example Suppose a 4600 kg elephant were placed on a see-saw with a 0. 025 kg mouse. The elephant is placed 10 meters from the point of rotation. If the plank is massless, how far from the point of rotation would the mouse need to be placed so that the system exists in a state of static equilibrium? If the plank magically gained mass after the mouse and elephant are balanced, what could you do to re-balance them?

Newton’s Second Law for Rotation If an object does experience a net torque, the object will have angular acceleration. We can modify Newton’s second law to account for rotation. When using this formula, it is beneficial to draw a free body diagram for the object. When dealing with rotation, each force should be drawn from its point of origin (gravity starts at the center, normal force at the point of contact, ect. ). § This makes it easier to see which forces provide torques and which ones don’t. § §

Drawing Parallels

Example A baseball bat has a mass of 0. 82 kg and is 0. 86 m long. It’s held vertically and then allowed to fall. What is the bat’s angular acceleration when it has reached 20° from the vertical? (Model the bat as a uniform cylinder).

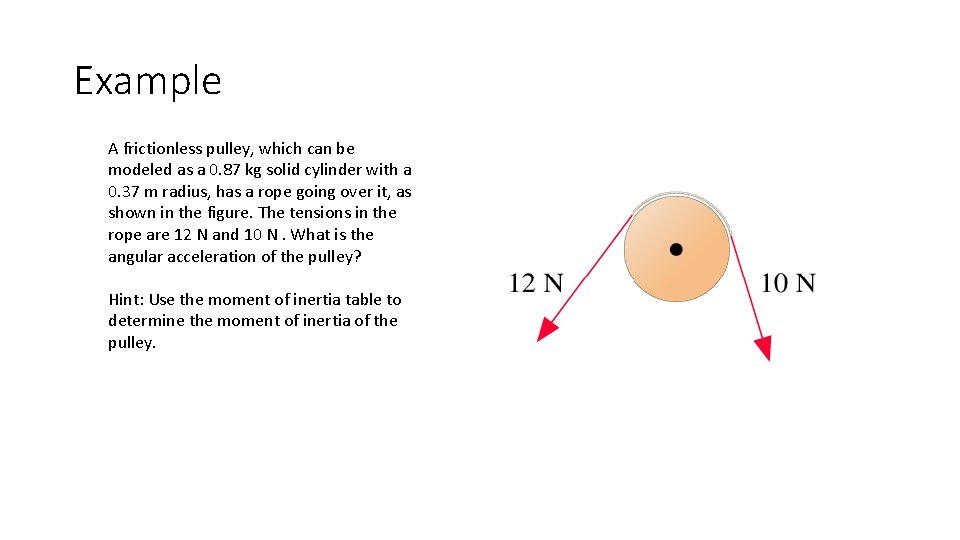
Example A frictionless pulley, which can be modeled as a 0. 87 kg solid cylinder with a 0. 37 m radius, has a rope going over it, as shown in the figure. The tensions in the rope are 12 N and 10 N. What is the angular acceleration of the pulley? Hint: Use the moment of inertia table to determine the moment of inertia of the pulley.

Constraints Due to Ropes and Pulleys § If the pulley turns without the rope slipping on it then the rope’s speed must exactly match the speed of the rim of the pulley. § The attached object must have the same speed and acceleration as the rope. § In addition, when the pulley has mass, the tension are not necessarily equal on both sides (they are only equal when the net torque on the pulley is equal to zero).

Rolling Motion and Energy

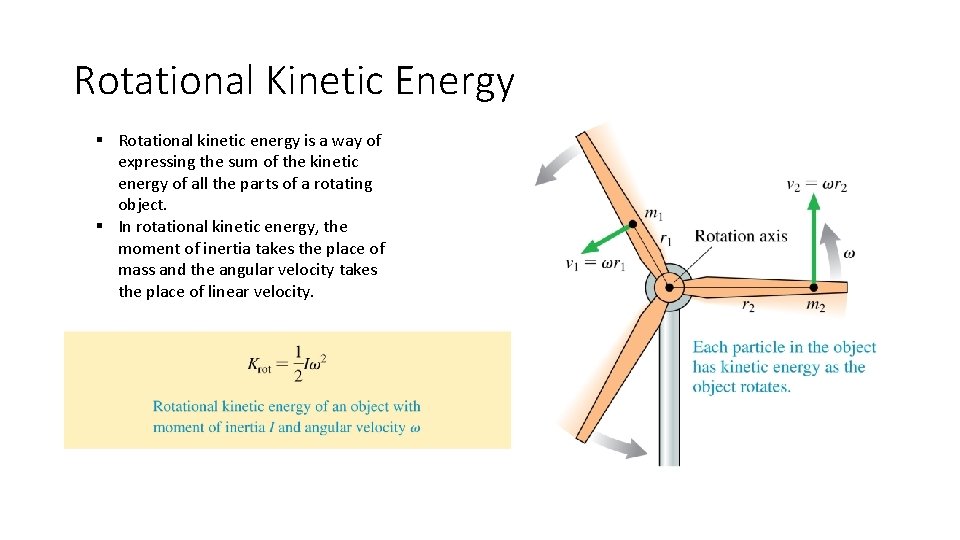
Rotational Kinetic Energy § Rotational kinetic energy is a way of expressing the sum of the kinetic energy of all the parts of a rotating object. § In rotational kinetic energy, the moment of inertia takes the place of mass and the angular velocity takes the place of linear velocity.

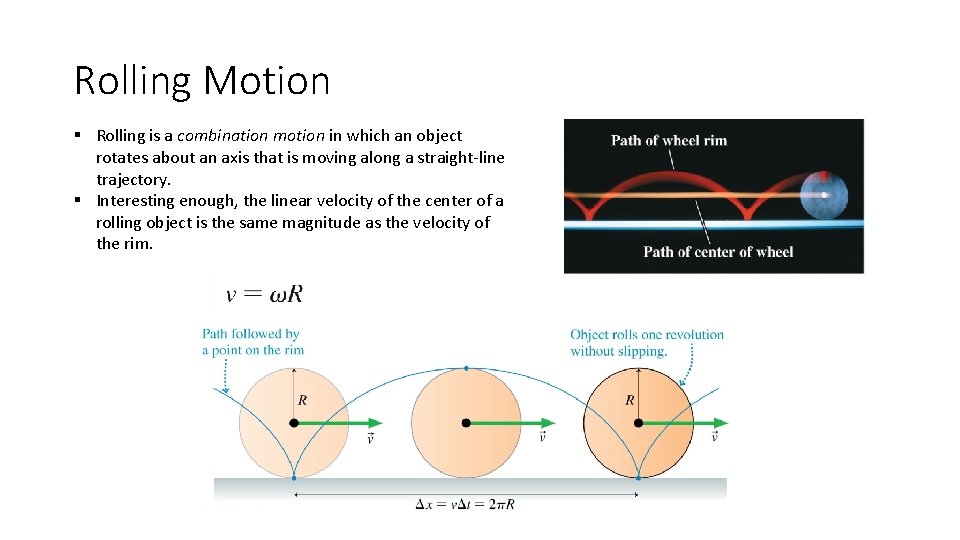
Rolling Motion § Rolling is a combination motion in which an object rotates about an axis that is moving along a straight-line trajectory. § Interesting enough, the linear velocity of the center of a rolling object is the same magnitude as the velocity of the rim.

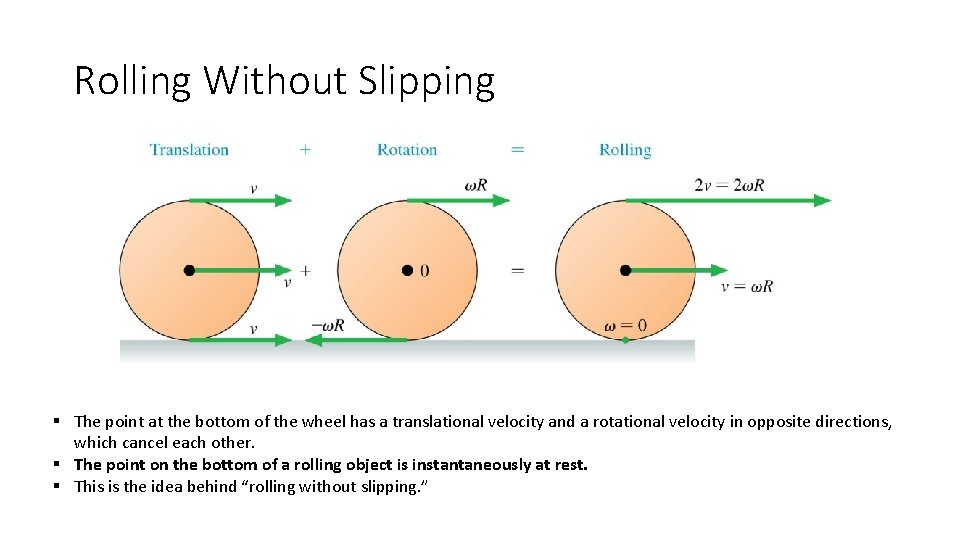
Rolling Without Slipping § The point at the bottom of the wheel has a translational velocity and a rotational velocity in opposite directions, which cancel each other. § The point on the bottom of a rolling object is instantaneously at rest. § This is the idea behind “rolling without slipping. ”

Dynamics of a Rolling Ball § A common problem in physics involves a ball rolling down a ramp. § The ball only rolls down the ramp because of static friction. This is because static friction is the only force that provides torque (which causes it to roll). § If there were no friction, the ball would slide down the ramp instead of rolling. § Because of friction, the ball is moving slower at the bottom of the ramp than it would have if it had slid down a frictionless ramp.

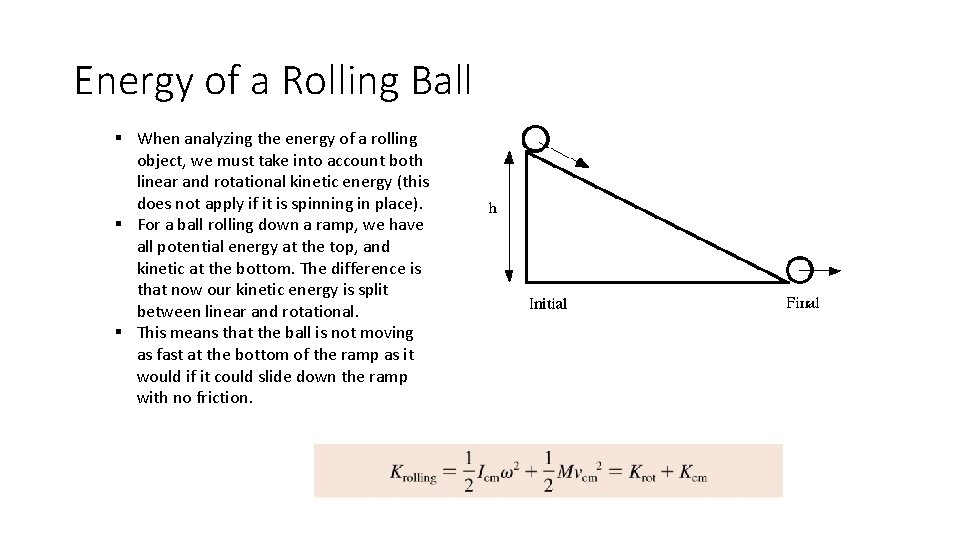
Energy of a Rolling Ball § When analyzing the energy of a rolling object, we must take into account both linear and rotational kinetic energy (this does not apply if it is spinning in place). § For a ball rolling down a ramp, we have all potential energy at the top, and kinetic at the bottom. The difference is that now our kinetic energy is split between linear and rotational. § This means that the ball is not moving as fast at the bottom of the ramp as it would if it could slide down the ramp with no friction.

Example A very common problem is to find the velocity of a ball rolling down an inclined plane. It is important to realize that you cannot work out this problem the way you used to. In the past, everything was SLIDING. Now the object is rolling and thus has MORE energy than normal. So let’s assume the ball is like a thin spherical shell and was released from a position 5 m above the ground. Calculate the velocity at the bottom of the incline. If you HAD NOT included the rotational kinetic energy, you see the answer is very much different. 7. 67 m/s

Angular Motion Vectors

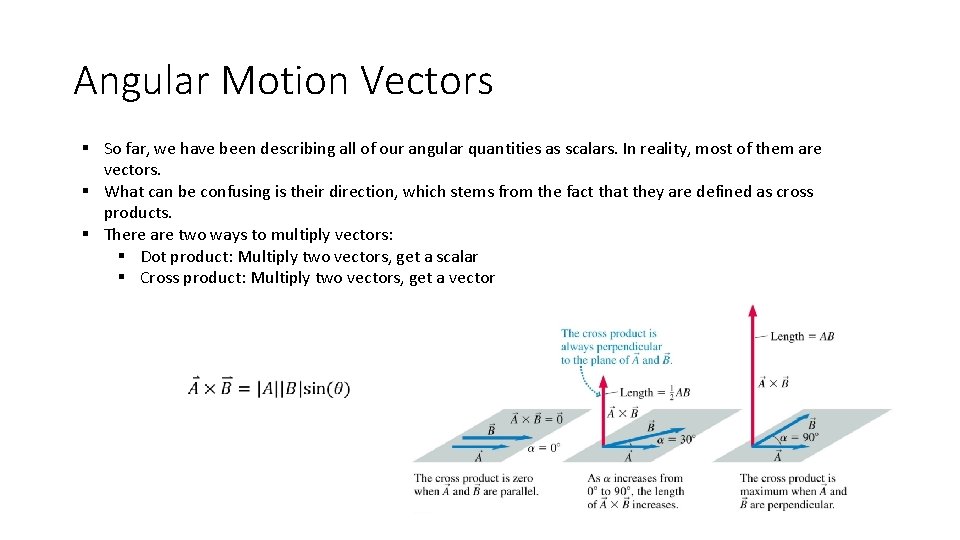
Angular Motion Vectors § So far, we have been describing all of our angular quantities as scalars. In reality, most of them are vectors. § What can be confusing is their direction, which stems from the fact that they are defined as cross products. § There are two ways to multiply vectors: § Dot product: Multiply two vectors, get a scalar § Cross product: Multiply two vectors, get a vector

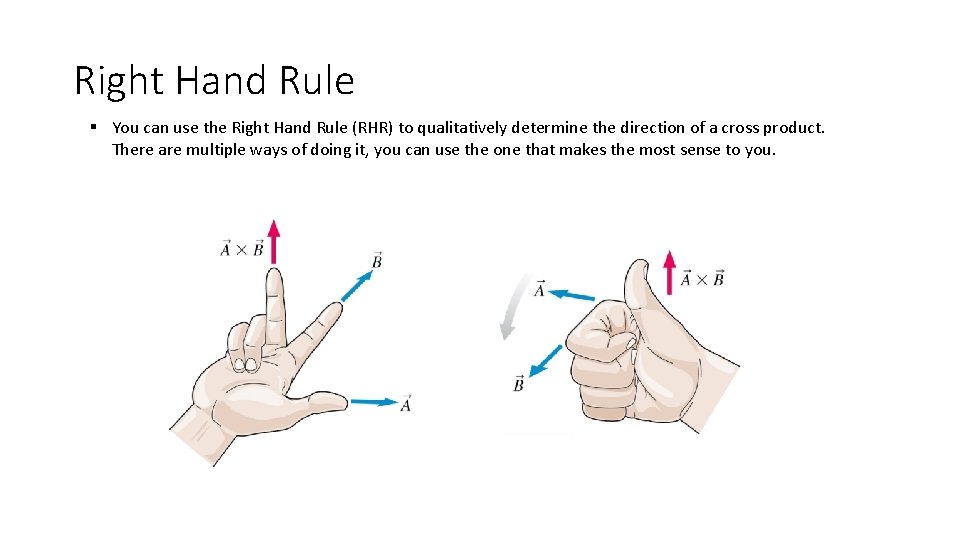
Right Hand Rule § You can use the Right Hand Rule (RHR) to qualitatively determine the direction of a cross product. There are multiple ways of doing it, you can use the one that makes the most sense to you.

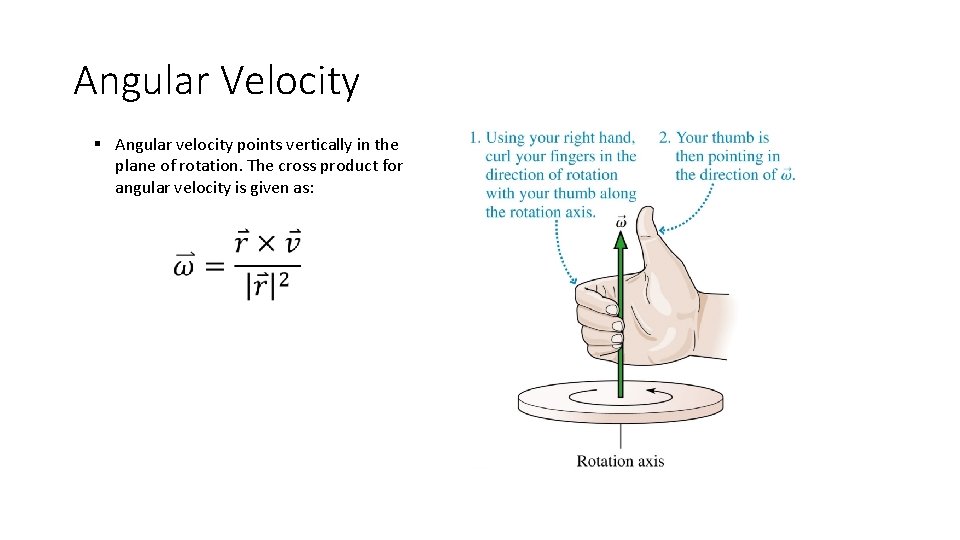
Angular Velocity § Angular velocity points vertically in the plane of rotation. The cross product for angular velocity is given as:

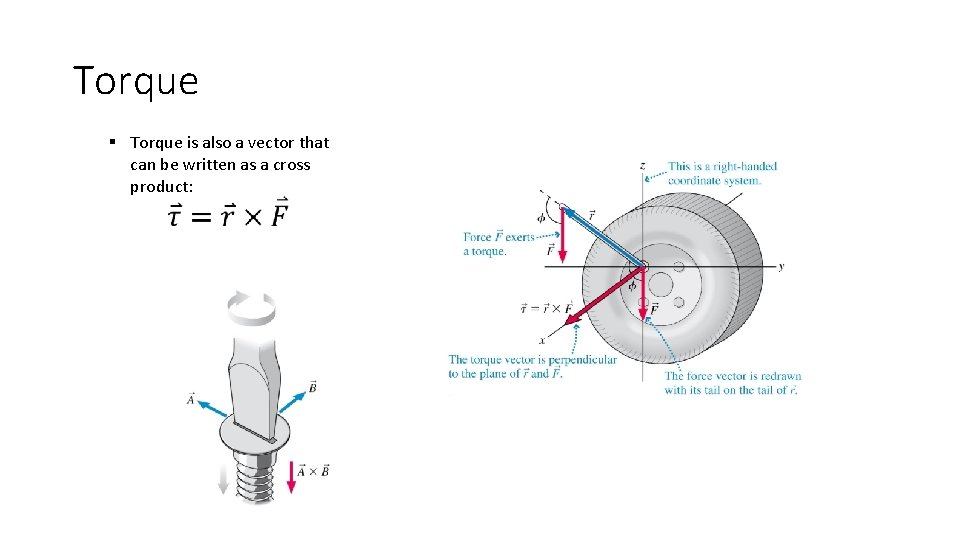
Torque § Torque is also a vector that can be written as a cross product:

Angular Momentum

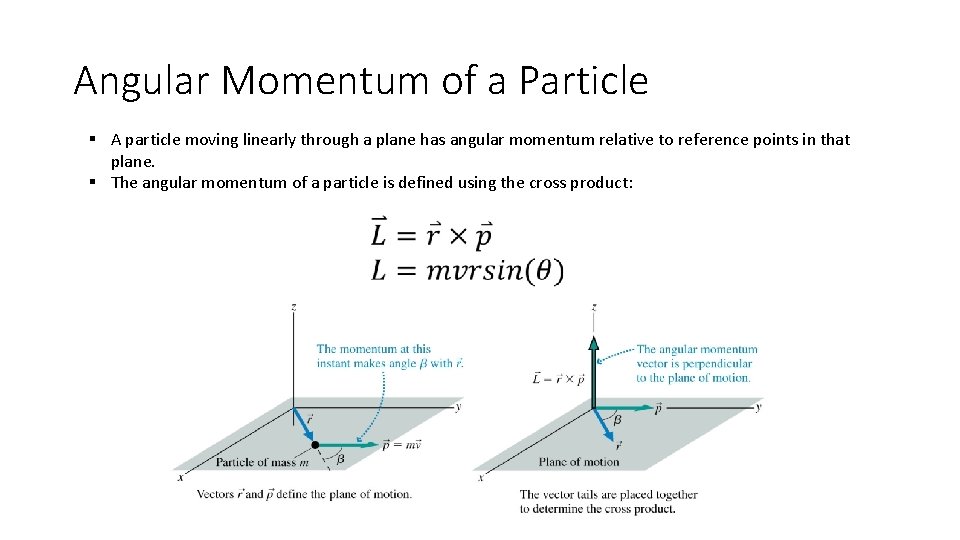
Angular Momentum of a Particle § A particle moving linearly through a plane has angular momentum relative to reference points in that plane. § The angular momentum of a particle is defined using the cross product:

Torque-Angular Momentum Relationship § In linear motion, we found that there was a relationship between net force and change in momentum, given by the equation below: § This same relationship exists between net torque and change in angular momentum: § This is essentially impulse-momentum theorem in angular form.

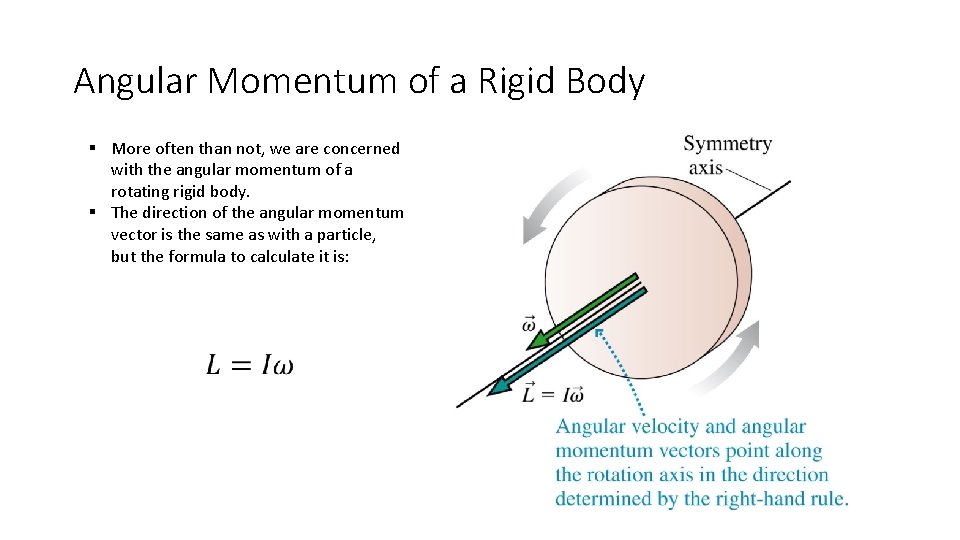
Angular Momentum of a Rigid Body § More often than not, we are concerned with the angular momentum of a rotating rigid body. § The direction of the angular momentum vector is the same as with a particle, but the formula to calculate it is:

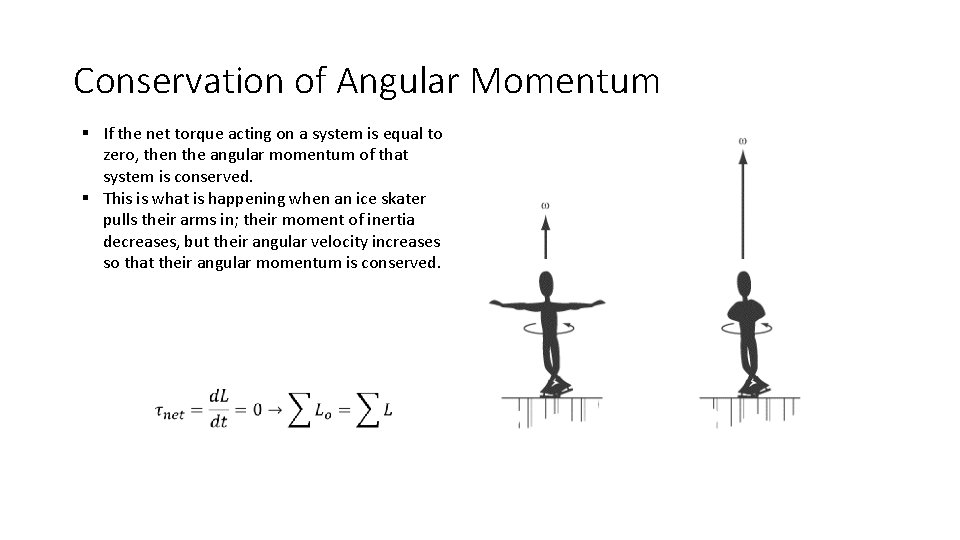
Conservation of Angular Momentum § If the net torque acting on a system is equal to zero, then the angular momentum of that system is conserved. § This is what is happening when an ice skater pulls their arms in; their moment of inertia decreases, but their angular velocity increases so that their angular momentum is conserved.

Example A bakery creates two perfectly identical bagels. The bagels are perfectly aligned so that one bagel is directly above the other. The bagels begin to spin and the top bagel is dropped on the lower one. After a brief period of the bagels grinding on each other (everything bagels have a lot of friction, stupid poppy seeds), they rotate in the same direction at the same speed. Determine that speed for the following scenarios: Top bagel is spinning at 10 RPM CW, bottom bagel is not spinning. Top bagel is spinning at 20 RPM CW, bottom bagel is spinning at 10 RPM CCW. Top bagel is spinning at 15 RPM CW, bottom bagel is spinning at 15 RPM CCW. Top bagel is spinning at 5 RPM CW, bottom bagel is spinning at 5 RPM CCW.

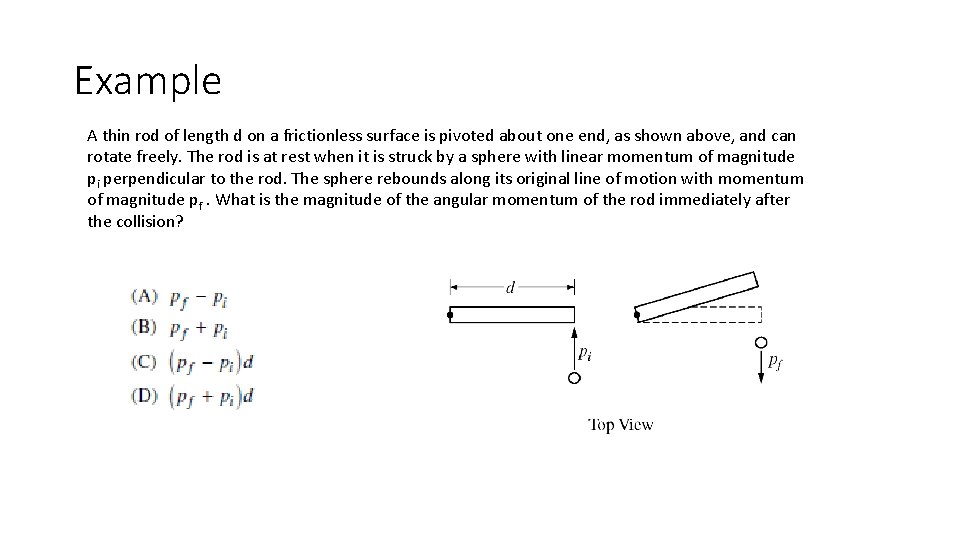
Example A thin rod of length d on a frictionless surface is pivoted about one end, as shown above, and can rotate freely. The rod is at rest when it is struck by a sphere with linear momentum of magnitude pi perpendicular to the rod. The sphere rebounds along its original line of motion with momentum of magnitude pf. What is the magnitude of the angular momentum of the rod immediately after the collision?