Rigid Body Motion Game Physics Linear physics physics

Rigid Body Motion

Game Physics • “Linear physics”– physics of points – particle systems, ballistic motion… – key simplification: no orientation • “Rotational physics” – orientation can change

Rigid Bodies No longer points: distribution of mass instead. Rigid bodies: distances between mass elements never change. Orientation of body can change over time.

Rigid Body Translation • Can treat translational motion of rigid bodies exactly the same as points • Single position (position of center of mass) • F=ma (external forces) • v = ∫a dt • x = ∫v dt • momentum conservation

Rotation • Rigid bodies also have orientation • Treating rotation properly is complicated • Rotation is not a vector (rotations do not commute, i. e. , order of rotations matters) • No analog to x, v, a in rotations?

Angular velocity • Infinitesimally small rotations do commute • Suppose we have a rigid body rotating about an axis • Can use a notion of angular velocity: • ω = dθ/dt

Angular velocity • Connection between linear and angular velocity • Magnitudes: v = ωrperp • Want vector relation • Nice to have angular velocity about axis of rotation (so it doesn't have to change all the time for an object spinning in place) • Let v = ω x r

Angular velocity • v=ωxr • Or, ω = r x v / |r|2 • Note: ω, r, v vectors • Angular velocity defined this way so that constant angular velocity behaves sensibly – spinning top has constant ω

Applying force • What happens when you push on a spinning object? (exert force) • F=ma, so we know the movement of the centre of mass • How does the force affect orientation?

Torque • T=rx. F • r is vector from origin to location where force applied – for convenience, often take origin to be center of mass of object • F is force • Magnitude proportional to force, proportional to distance from origin

Intuition for Torque • Larger the larger from the centre • Lever action: small force yields equivalent torque far from fulcrum

Direction of Torque • T=rx. F • Perpendicular to both location and force vectors • Direction is along axis about which rotation is induced • Right hand rule: thumb along axis, fingers curl in direction of rotation
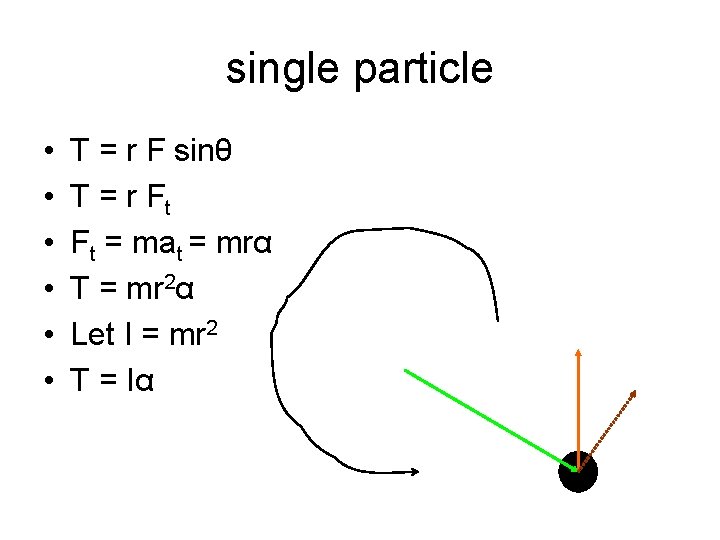
single particle • • • T = r F sinθ T = r Ft Ft = mat = mrα T = mr 2α Let I = mr 2 T = Iα

Many particles • Real objects are (pretty much) continuous • Game objects: distribution of point masses – not always, but common • Can get reasonable behaviour with (e. g. ) four point masses per rigid body • Single orientation for body • Single centre of mass (of course)

Changing Coordinate Systems • We dealt with changing coordinate systems all the time before • Rigid bodies are much simpler if we treat them in a natural coordinate system – origin at the centre of mass of the body – or, some other sensible origin: hinge of door • Need to transform forces into body coordinate system to calculate torque • Transform motion back to world space

Angular momentum • Define angular momentum similarly to torque: • L=rxp • Note that with this definition, T = d. L/dt, just as F = dp/dt

Force and Torque • Note: a force is a force and a torque • Moves body linearly: F=ma, changes linear momentum • Rotates body: produces torque, changes angular momentum

Linear vs. Angular linear quantity angular quantity velocity v angular velocity ω acceleration a angular acc. α mass m moment of inertia I p = mv L = Iω F = ma T = Iα

Conservation of Angular Momentum • Consequence of T = d. L/dt: – If net torque is zero, angular momentum is unchanged • Responsible for gyroscopes' unintuitive behaviour The gyroscope is tipped over but it doesn’t fall

Moment of Inertia • Said that moment of inertia of a point particle is mr^2 • In the general case, I = ∫ ρ r^2 d. V where r is the distance perpendicular to the axis of rotation • Don't know the axis of rotation beforehand

Moment of Inertia • I = ∫ρ(x, y, z) y^2 + z^2 -xy -xz -xy x^2 + z^2 -yz -xz -yz dxdydz x^2+y^2

Diagonalized Moment of Inertia • Luckily, we can choose axes (principal axes of the body) so that the matrix simplifies: Ixx 0 • I= 0 0 Iyy 0 0 0 Izz • where, e. g. , Ixx = m(y*y + z*z) • Off-diagonal entries called "products of inertia"

Avoiding products of inertia • Do calculations in inertial reference frame whose axes line up with the principal axes of your object • Transform the results into worldspace • Moment of inertia of a body fixed, so can be precomputed and used at run-time

Moment of Inertia • In general, the more compact a body is, the smaller the moments of inertia, and the faster it will spin (for the same torque)

Fake I • Not doing engineering simulation (prediction of how real objects will behave) • Can invent I rather than integrating • Large values: hard to rotate about this axis • Avoid off-diagonal elements

Fake constants • For that matter, can fake lots of stuff • Different gravity for different objects – e. g. , slow bullets in FPS – e. g. , fast falling in platformer • fake forces, approximate bounding geometry

Case in 2 D • In 2 D, the vectors T, ω, α become scalars (their direction is known – only magnitude is needed) • Moment of inertia becomes a scalar too: • I = ∫prd. A

Single planar rigid body • state contains x, y, θ, vx, vy, ω • Have – F = ma (2 equations) – T = Iω – x = ∫vx dt – y = ∫vy dt – θ = ∫ω dt • Integrate to obtain new state, and proceed

Rigid body in 3 D • Need some way to represent general orientation • Need to be able to compose changes in orientation efficiently

Quaternions • Quaternion: structure for representing rotation – unit vector (axis of rotation) – scalar (amount of rotation) – recall, store (cos(θ/2), v sin(θ/2) ) • Can represent orientation as quaternion, by interpreting as rotation from canonical position

Quaternions • Rotation of θ about axis v: – q = (cos(θ/2), v sin(θ/2)) • "Unit quaternion": q. q = 1 (if v is a unit vector) • Maintain unit quaternion by normalizing v • Arbitrary vector r can be written in quaternion form as (0, r)

Quaternion Rotation • To rotate a vector r by θ about axis v: – take q = (cos(θ/2), v sin(θ/2) – Let p = (0, r) – obtain p' from the quaternion resulting from qpq-1 – p' = (0, r') – r' is the rotated vector r

Rotation Differentiation • Note: – q(t) = (s(t), v(t)) – q(t) = [ cos(θ(t)/2), u sin(θ(t)/2) ] – For a body rotating with constant angular velocity ω, it can be shown • q’(t) = [0, ½ ω] q(t) • Summarize this ½ ω q(t)
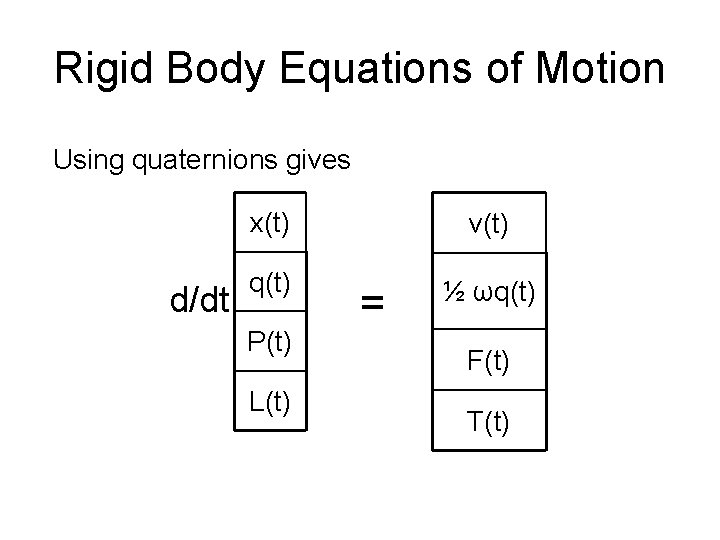
Rigid Body Equations of Motion Using quaternions gives d/dt x(t) v(t) q(t) ½ ωq(t) P(t) L(t) = F(t) T(t)

P and L • Note that – v = P/m (from P=mv) – ω = I-1 L (from L = Iω) • Often useful to use momentum variables as main variables, and only compute v and ω (auxiliary variables) as needed for the integration

Impulse • Sudden change in momentum – also, angular momentum (impulsive torque) • Collision resolution using impulse – new angular momentum according to conditions of collision – algorithmic means available for resolving
- Slides: 38