ROTATIONAL MOTION AND THE LAW OF GRAVITY Ch

ROTATIONAL MOTION AND THE LAW OF GRAVITY Ch 7:

MEASURING ROTATIONAL MOTION: Motion of a body that spins about an axis. Ex: Ferris Wheel � Any point on a Ferris wheel that spins about a fixed axis undergoes circular motion. � To analyze the motion is it convenient to set up a fixed reference line. And assume that at time t=0, a cart is on the reference line. Reference line

After time interval t 2 the cart advances to a new position. In this time interval, the line from the center to the cart moved through angle theta with respect to the reference line. Likewise, the cart moved a distance s, measured from the circumference of the circle; s is arc length. Cart (at time t 2) s Reference line

THETA AND ARC DISTANCE (S) If the cart moves through an angle twice as large, How would the new distance compare with the distance shown here represented by s? Cart (at time t 2) s Reference line

THETA AND ARC DISTANCE (S) If the cart moves through an angle twice as large, How would the new distance compare with the distance shown here represented by s? THE NEW DISTANCE WOULD BE TWICE AS LARGE! Cart (at time t 2) s Reference line

ANGLES CAN BE MEASURED IN RADIANS ***ALMOST ALL EQUATIONS IN THIS CHAPTER AND THE NEXT REQUIRE THAT ANGLES BE MEASURED IN RADIANS*** Radian an angle whose arc length is equal to the radius, which is approximately equal to 57. 3 degrees.

ANGLES IN RADIANS… Any angle theta measured in radians is defined by: Theta = s (arc length) r (radius) Radian is a pure number, with NO dimensions. Units cancel, and we use the abbreviation rad to identify unit.

CIRCUMFERENCE… When the cart of the Ferris wheel from our previous example goes through an angle of 360 degrees. The arc length s is equal to the circumference of the circle, or 2 π r Thus, theta = s = 2πr = 2 π rad r r

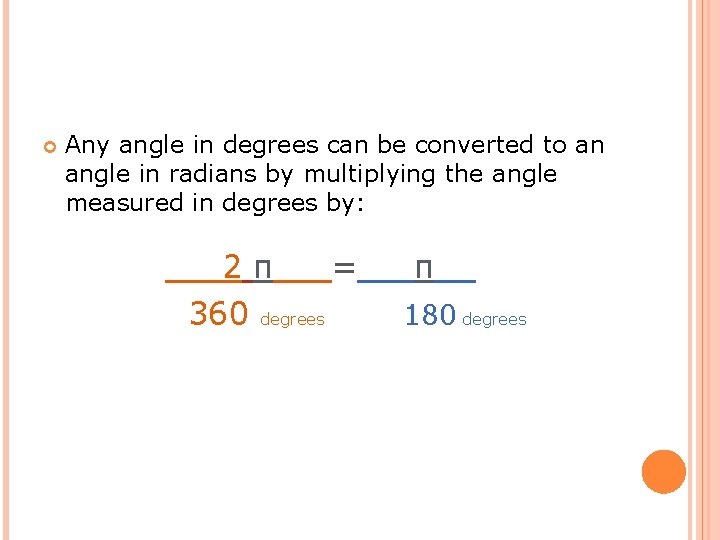
Any angle in degrees can be converted to an angle in radians by multiplying the angle measured in degrees by: 2π = 360 degrees π 180 degrees

Angular motion is measured in units of radians. Because there are 2 π radians in a full circle, radians are often expressed as a multiple of π.

Look at Figure 7 -3 in your text on page 245 Determine the radian measure equivalent to 75 degrees.

Look at Figure 7 -3 in your text on page 245 Determine the radian measure equivalent to 75 degrees. _5 12 π

ANGULAR DISPLACEMENT Describes how much an object has rotated Book Definition: the angle through which a point, line, or body is rotated in a specified direction and about a specified axis. EQUATION: Angular displacement (in radians)= Change in arc length Distance from axis OR θ=� s/r

EXAMPLE: Earth has an equatorial radius of approximately 6380 km and rotates 360 degrees every 24 hours. What is the angular displacement (in degrees) of a person standing at the equator for 1 hour?

EXAMPLE: Earth has an equatorial radius of approximately 6380 km and rotates 360 degrees every 24 hours. What is the angular displacement (in degrees) of a person standing at the equator for 1 hour? θ = 360/24 = 15 degrees

EXAMPLE: Earth has an equatorial radius of approximately 6380 km and rotates 360 degrees every 24 hours. Convert the angular displacement (in degrees) to radians.

EXAMPLE: Earth has an equatorial radius of approximately 6380 km and rotates 360 degrees every 24 hours. Convert the angular displacement (in degrees) to radians. θ (rad) = π /180 (θ deg) = π /180 (15 deg) θ (rad) = 0. 26 rad

EXAMPLE: Earth has an equatorial radius of approximately 6380 km and rotates 360 degrees every 24 hours. What is the arc length traveled by this person?

EXAMPLE: Earth has an equatorial radius of approximately 6380 km and rotates 360 degrees every 24 hours. What is the angular displacement (in degrees) of a person standing at the equator for 1 hour? θ=� s/r (r) θ = � s (6380) (0. 26) = 1658. 8 km ~1700 km

ANGULAR SPEED… Describes rate of rotation The average angular speed, θ avg, is the ratio between the angular displacement, θ, to the time interval, t, that the object takes to undergo that displacement. θ avg = θ / t Units are given in rad/s

EXAMPLE An Indy car can complete 120 laps in 1. 5 hours. Even though the track is an oval rather than a circle, you can still find the angular speed. Calculate the average angular speed of the Indy car.

EXAMPLE An Indy car can complete 120 laps in 1. 5 hours. Even though the track is an oval rather than a circle, you can still find the angular speed. Calculate the average angular speed of the Indy car. 1: Convert hours to seconds. 2: Convert total angular displacement from degrees to radians 3: Solve for average angular velocity. 1. 5 hrs = 1. 5 * 60 = 5400 s θ = 360 deg * 120 = 43200 degrees = 43200 (π /180) = 753. 98 radians � avg = θ / t � avg = 753. 98 rad / 5400 s � avg = 0. 1396 = 0. 14 rad/s

ANGULAR ACCELERATION Occurs when angular speed changes It is the time rate of change of angular speed, expressed in radians per second (think about linear acceleration units…m/s/s or m/s 2) Equation: �� avg = θ θ 1 = �θ t 2 - t 1 t 2 - = change in angular speed time interval

EXAMPLE… A top that is spinning at 15 rev/s spins for 55 s before coming to a stop. What is the average acceleration of the top while it is slowing?

EXAMPLE… A top that is spinning at 15 rev/s spins for 55 s before coming to a stop. What is the average acceleration of the top while it is slowing? � avg = θ 2 - θ 1 = �θ = change in angular speed t 2 - t 1 t time interval � avg = 15 (360) = 0 - 5400 55 55 =98. 18 (π /180) = - 1. 7 rad/s/s

HOMEWORK TONIGHT… PAGE 247 # 1 and 3 Page 248 # 1 Page 250 # 1 and 2 READ 7 -1 and 7 -2

Q. O. T. D. 12 -1 -2009 Convert the following from degrees to radians: a. 17 deg b. 50 deg c. 170 deg d. 270 deg • What is the ratio that defines the average angular speed? • When a wheel rotates about a fixed axis, do all points on the wheel have the same angular speed?

QOTD- ANSWERS 1 a. 0. 297 rad c. 2. 967 rad b. 0. 873 rad d. 4. 712 rad 2 - wavg = change in angular displacement time interval. delta theata/delta time (rad/s) 3 - YES. Otherwise, the wheel would change shape!

ROTATIONAL MOTION TANGENTIAL AND CENTRIPETAL ACCELERATION Ch 7: Section 2

TANGENTIAL SPEED The instantaneous linear speed of an object along the tangent to the object’s circular path. Objects in circular motion have a tangential speed.

TANGENTIAL SPEED A point on an object rotating about a fixed axis has tangential speed related to the object’s angular speed. When the object’s angular acceleration changes, the tangential acceleration of a point on the object changes.

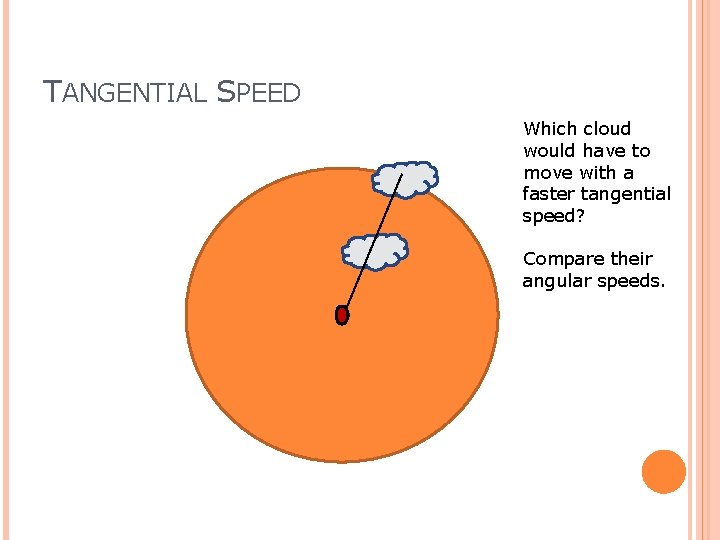
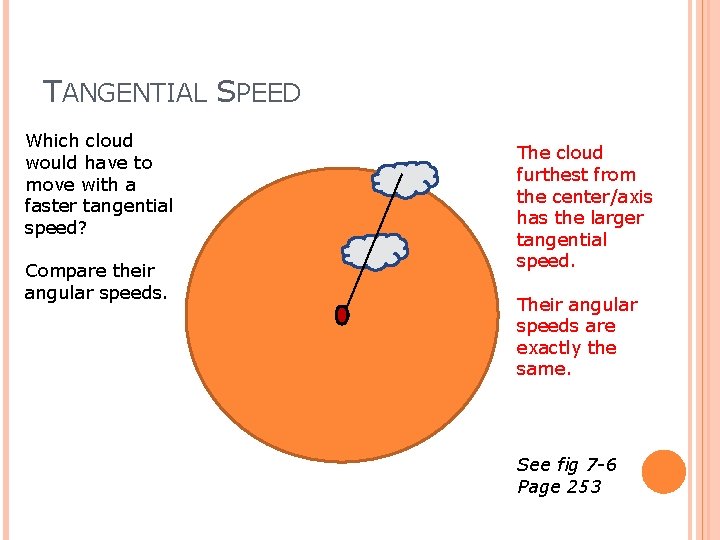
TANGENTIAL SPEED Which cloud would have to move with a faster tangential speed? Compare their angular speeds.

TANGENTIAL SPEED Which cloud would have to move with a faster tangential speed? Compare their angular speeds. The cloud furthest from the center/axis has the larger tangential speed. Their angular speeds are exactly the same. See fig 7 -6 Page 253

HOW DO YOU CALCULATE TANGENTIAL SPEED? Remember that… Angular displacement = change in arc length/radius or delta theta = delta s/r Average angular speed = angular displacement/time or wavg = delta theta/delta t Vt = r ω Tangential Speed = radius x angular speed

TANGENTIAL SPEED A golfer has a max angular speed of 6. 3 rad/s for her swing. She can choose between two drivers, one placing the club head 1. 9 m from her axis of rotation, and the other placing it 1. 7 m from the axis. 1. Calculate the tangential speed of the club head for each driver. 2. All other factors being equal, which driver is likely to hit the ball farther?

TANGENTIAL SPEED A golfer has a max angular speed of 6. 3 rad/s for her swing. She can choose between two drivers, one placing the club head 1. 9 m from her axis of rotation, and the other placing it 1. 7 m from the axis. 1. Calculate the tangential speed of the club head for each driver. Vt = rω = 1. 9 (6. 3) = 11. 97 ~ 12 m/s Vt = rω= 1. 7 (6. 3) = 10. 71 ~ 11 m/s

TANGENTIAL SPEED A golfer has a max angular speed of 6. 3 rad/s for her swing. She can choose between two drivers, one placing the club head 1. 9 m from her axis of rotation, and the other placing it 1. 7 m from the axis. 2. All other factors being equal, which driver is likely to hit the ball farther? The longer driver will hit the ball further because its club head has a higher tangential speed.

TANGENTIAL SPEED EXAMPLE… A softball pitcher throws a ball with a tangential speed of 6. 93 m/s. If the pitcher’s are is 0. 66 m long, what is the angular speed of the ball before the pitcher releases it?

TANGENTIAL SPEED EXAMPLE… A softball pitcher throws a ball with a tangential speed of 6. 93 m/s. If the pitcher’s are is 0. 66 m long, what is the angular speed of the ball before the pitcher releases it? Vt = r ω 6. 93 = 0. 66 (ω) 6. 93/0. 66 = ω W = 10. 5 rad/s

TANGENTIAL SPEED A point on an object rotating about a fixed axis has tangential speed related to the object’s angular speed. When the object’s angular acceleration changes, the tangential acceleration of a point on the object changes.

TANGENTIAL ACCELERATION Tangential Acceleration is tangent to a CIRCULAR path It is the instantaneous linear acceleration of an objected directed along the tangent to the object’s circular path. EQUATION for Tangential Acceleration: a t= r α Tangential acceleration = radius x angular acceleration

EXAMPLE… A yo-yo has a tangential acceleration of 0. 98 m/s/s when it is released. The string is wound around a central shaft of radius 0. 35 cm. What is the angular acceleration of the yo-yo?

EXAMPLE… A yo-yo has a tangential acceleration of 0. 98 m/s/s when it is released. The string is wound around a central shaft of radius 0. 35 cm. What is the angular acceleration of the yo-yo? 0. 35 cm = 0. 0035 m a t= r α 0. 98 = 0. 0035 (α) 0. 98/. 0035 = α 280 rad 2 = α

CENTRIPETAL ACCELERATION The acceleration directed toward the center of a circular path. An acceleration due to a change in direction-even when an object is moving at a constant speed) Given by…. Ac = vt 2/r Can also be found using the angular speed… Ac = ω2 x r

UNIFORM CIRCULAR MOTION Uniform circular motion occurs when an acceleration of constant magnitude is perpendicular to the tangential velocity.

TANGENTIAL VS. CENTRIPETAL ACCELERATION Centripetal and tangential acceleration are NOT the same. The tangential component of acceleration is due to changing speed The centripetal component of acceleration is due to changing direction.

REVIEW QUESTIONS… Describe the path of a moving body whose acceleration is constant in magnitude at all times and is perpendicular to the velocity. An object moves in a circular path with a constant speed, v. Is the objects velocity constant? Is its acceleration constant? Explain. Give an example of a situation in which an automobile driver can have a centripetal acceleration but no tangential acceleration.

Describe the path of a moving body whose acceleration is constant in magnitude at all times and is perpendicular to the velocity. A CIRCLE. An object moves in a circular path with a constant speed, v. Is the objects velocity constant? Is its acceleration constant? Explain. no. direction is changing. no. the direction of ac is changing, at = 0 Give an example of a situation in which an automobile driver can have a centripetal acceleration but no tangential acceleration. A car driving in a circle at a Constant Speed.

KEY TERMS TO KNOW FOR YOUR TEST FRIDAY… Angular Acceleration Angular Displacement Angular Speed Centripetal Acceleration Gravitational Force Radian Rotational Motion Tangential Acceleration Tangential Speed

DEMO LINKS http: //www. upscale. utoronto. ca/General. Inter est/Harrison/Flash/Class. Mechanics/Vert. Circul ar/Vert. Circular. html http: //www. upscale. utoronto. ca/General. Inter est/Harrison/Flash/Class. Mechanics/RTZCoord System/RTZCoord. System. html http: //w 3. shorecrest. org/~Lisa_Peck/Physics /syllabus/mechanics/circularmotion/hewitt/S ource_Files/08_Centripetal. Force_VID. mov

HOMEWORK! Read 7 -2 and 7 -3 Write out Key Term definitions in your own words on a sheet of notebook paper. Page 255 #1 Page 256 #1 -2 Page 258 #1 and 4

Q. O. T. D. If an object has a tangential acceleration of 10. 0 m/s/s, the angular speed will do which of the following? Decrease, • 12 -2 -2009 increase, or stay the same What is the tangential speed of a ball swung at a constant angular speed of 5. 0 rad/s on a rope that is 5. 0 m long?

QOTD- ANSWERS 1. increases 2. 25 m/s

CH 7 SECTION 3: CAUSES OF CIRCULAR MOTION Centripetal Force (Fc) = force that maintains circular motion Fc = mvt 2/r or Fc = mrω2 (Where m is mass of the object in motion) Force maintains circular motion and is measured in SI units of Newtons (N).

EXAMPLE A pilot is flying a small plane at 30. 0 m/s in a circular path with a radius of 100. 0 m. If a force of 635 N is needed to maintain the pilots circular motion, what is the pilot’s mass?

EXAMPLE A pilot is flying a small plane at 30. 0 m/s in a circular path with a radius of 100. 0 m. If a force of 635 N is needed to maintain the pilots circular motion, what is the pilot’s mass? Fc = mvt 2/r 635 = m (30 x 30)/(100) 635 = m (900/100) 635 = m (9) 635/9 = m 70. 55 kg = m

A FORCE DIRECTED TOWARD THE CENTER IS NECESSARY FOR CIRCULAR MOTION! If this force vanishes, an object does not continue to move in its circular path. Instead it moves along a straight-line path tangent to the circle. SEE FIG. 7 -11 If swinging a ball on a string…then the string breaks…

NEWTON’S LAW OF UNIVERSAL GRAVITATION Gravitational force is a field force that always exists between two masses regardless of size. Gravitational force acts such that objects are always attracted to one another. Gravitational force mutual force of attraction between two particles.

NEWTON’S LAW OF UNIVERSAL GRAVITATION Gravitational force depends on the distance between the two masses. If masses m 1 and m 2 are separated by some distance, r, the magnitude of gravitational force is given by: Fg = G x (m 1 m 2) r 2

NEWTON’S LAW OF UNIVERSAL GRAVITATION G is a universal constant, constant of universal gravitation G = 6. 673 x 10 -11 Nm 2/kg 2 The law of universal gravitation is an example of an inverse square law; i. e. the force between two masses decreases as the masses move further apart.

EXAMPLE… Find the distance between a 0. 3 kg billiard ball and a 0. 4 kg billiard ball if the magnitude of the gravitational force is 8. 92 x 10 -11 N.

EXAMPLE… Find the distance between a 0. 3 kg billiard ball and a 0. 4 kg billiard ball if the magnitude of the gravitational force is 8. 92 x 10 -11 N. m 1 = 0. 3 kg r=? m 2 = 0. 4 kg Fg = 8. 92 x 10 -11 N Fg = G x (m 1 m 2) r 2 = (G/ Fg )(m 1 m 2) = (6. 673 x 10 -11/ 8. 92 x 10 -11 )(0. 3 X 0. 4) √ r 2 = √ 8. 97 x 10 -2 m 2 r = 0. 30 m

REVIEW/PRACTICE PROBLEMS… Understand Practice Problems (shown in BOLD) on pages: 246(7 A) 248 (7 B) 249(7 C) 251 (7 D) 254 (7 E) 256 (7 F) 258 (7 G) 261 (7 H) 264 (7 I)