2011 Pearson Education Inc Statistics for Business and

Statistics for Business and Economics Chapter 6 Inferences Based on a Single Sample: Tests

Content 1. The Elements of a Test of Hypothesis 2. Formulating Hypotheses and Setting Up the Rejection Region 3. Test of Hypothesis about a Population Mean: Normal (z) Statistic 4. Observed Significance Levels: p-Values 5. Test of Hypothesis about a Population Mean: Student’s t-Statistic © 2011 Pearson Education, Inc

Content 6. Large-Sample Test of Hypothesis about a Population Proportion 7. Calculating Type II Error Probabilities: More about * 8. Test of Hypothesis about a Population Variance © 2011 Pearson Education, Inc

Learning Objectives 1. Test a specific value of a population parameter (mean or proportion), called a test of hypothesis 2. Provide a measure of reliability for the hypothesis test, called the significance level of the test © 2011 Pearson Education, Inc

6. 1 The Elements of a Test of Hypothesis © 2011 Pearson Education, Inc

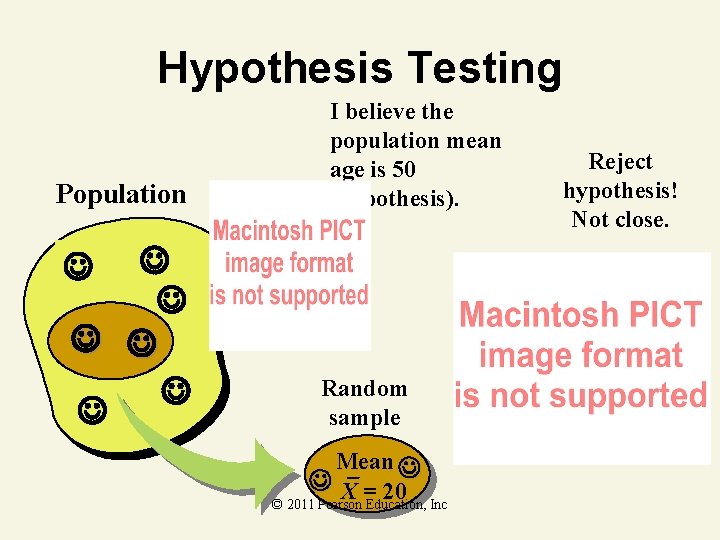
Hypothesis Testing Population I believe the population mean age is 50 (hypothesis). Random sample

What’s a Hypothesis? A statistical hypothesis is a statement about the numerical value of a population parameter. I believe the mean GPA of this class is 3. 5! © 2011 Pearson Education, Inc © 1984 -1994 T/Maker Co.

Null Hypothesis The null hypothesis, denoted H 0, represents the hypothesis that will be accepted unless the data provide convincing evidence that it is false. This usually represents the “status quo” or some claim about the population parameter that the researcher wants to test. © 2011 Pearson Education, Inc

Alternative Hypothesis The alternative (research) hypothesis, denoted Ha, represents the hypothesis that will be accepted only if the data provide convincing evidence of its truth. This usually represents the values of a population parameter for which the researcher wants to gather evidence to support. © 2011 Pearson Education, Inc

Alternative Hypothesis 1. Opposite of null hypothesis 2. The hypothesis that will be accepted only if the data provide convincing evidence of its truth 3. Designated Ha 4. Stated in one of the following forms Ha: some value) © 2011 Pearson Education, Inc

Identifying Hypotheses Example problem: Test that the population mean is not 3 Steps: • State the question statistically ( 3) • State the opposite statistically ( = 3) — Must be mutually exclusive & exhaustive • Select the alternative hypothesis ( 3) — Has the , <, or > sign • State the null hypothesis ( = 3) © 2011 Pearson Education, Inc

What Are the Hypotheses? Is the population average amount of TV viewing 12 hours? • State the question statistically: = 12 • State the opposite statistically: 12 • Select the alternative hypothesis: Ha: 12 • State the null hypothesis: H 0: = 12 © 2011 Pearson Education, Inc

What Are the Hypotheses? Is the population average amount of TV viewing different from 12 hours? • State the question statistically: 12 • State the opposite statistically: = 12 • Select the alternative hypothesis: Ha: 12 • State the null hypothesis: H 0: = 12 © 2011 Pearson Education, Inc

What Are the Hypotheses? Is the average cost per hat less than or equal to $20? • State the question statistically: 20 • State the opposite statistically: 20 • Select the alternative hypothesis: Ha: 20 • State the null hypothesis: H 0: 20 © 2011 Pearson Education, Inc

What Are the Hypotheses? Is the average amount spent in the bookstore greater than $25? • State the question statistically: 25 • State the opposite statistically: 25 • Select the alternative hypothesis: Ha: 25 • State the null hypothesis: H 0: 25 © 2011 Pearson Education, Inc

Test Statistic The test statistic is a sample statistic, computed from information provided in the sample, that the researcher uses to decide between the null and alternative hypotheses. © 2011 Pearson Education, Inc

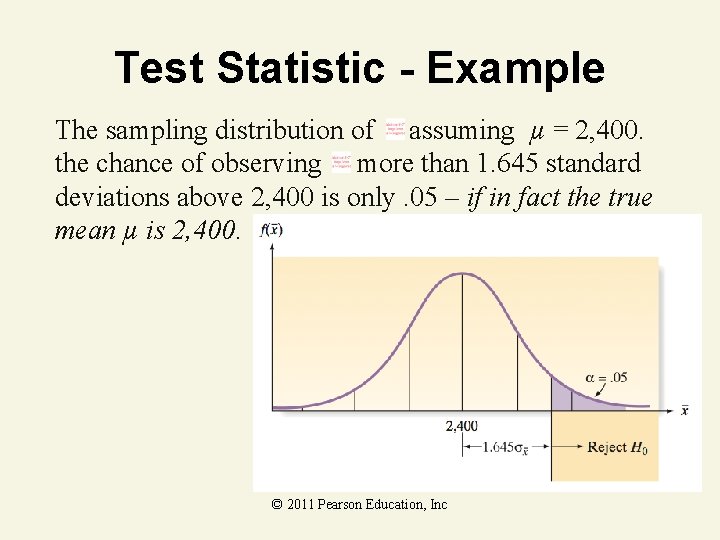
Test Statistic - Example The sampling distribution of assuming µ = 2, 400. the chance of observing more than 1. 645 standard deviations above 2, 400 is only. 05 – if in fact the true mean µ is 2, 400. © 2011 Pearson Education, Inc

Type I Error A Type I error occurs if the researcher rejects the null hypothesis in favor of the alternative hypothesis when, in fact, H 0 is true. The probability of committing a Type I error is denoted by . © 2011 Pearson Education, Inc

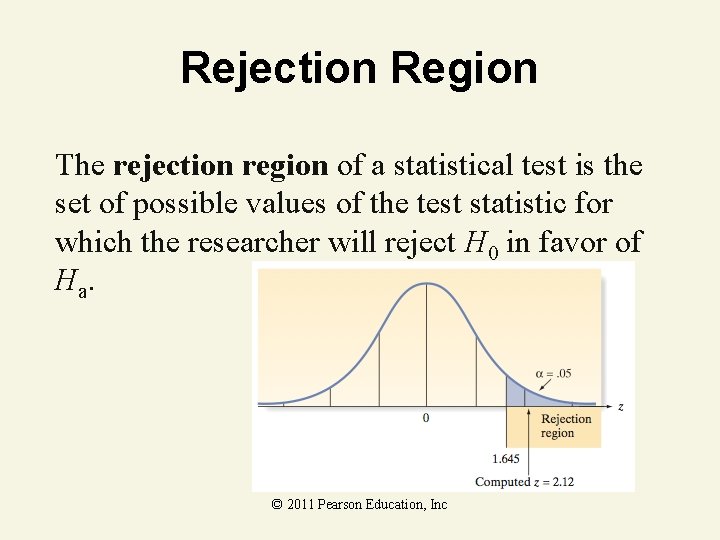
Rejection Region The rejection region of a statistical test is the set of possible

Type II Error A Type II error occurs if the researcher accepts the null hypothesis when, in fact, H 0 is false. The probability of committing a Type II error is denoted by . © 2011 Pearson Education, Inc

Conclusions and Consequences for a Test of Hypothesis True State of Nature Conclusion H 0 True Ha True Accept H 0 Correct decision Type II error (Assume H 0 True) (probability ) Reject H 0 (Assume Type I error Ha True) (probability ) © 2011 Pearson Education, Inc Correct decision

Elements of a Test of Hypothesis 1. Null hypothesis (H 0): A theory about the specific values of one or more population parameters. The theory generally represents the status quo, which we adopt until it is proven false. 2. Alternative (research) hypothesis (Ha): A theory that contradicts the null hypothesis. The theory generally represents that which we will adopt only when sufficient evidence exists to establish its truth. © 2011 Pearson Education, Inc

Elements of a Test of Hypothesis 3. Test statistic: A sample statistic used to decide whether to reject the null hypothesis. 4. Rejection region: The numerical values of the test statistic for which the null hypothesis will be rejected. The rejection region is chosen so that the probability is that it will contain the test statistic when the null hypothesis is true, thereby leading to a Type I error. The value of is usually chosen to be small (e. g. , . 01, . 05, or. 10) and is referred to as the level of significance of the test. © 2011 Pearson Education, Inc

Elements of a Test of Hypothesis 5. Assumptions: Clear statement(s) of any assumptions made about the population(s) being sampled. 6. Experiment and calculation of test statistic: Performance of the sampling experiment and determination of the numerical value of the test statistic. © 2011 Pearson Education, Inc

Elements of a Test of Hypothesis 7. Conclusion: a. If the numerical value of the test statistic falls in the rejection region, we reject the null hypothesis and conclude that the alternative hypothesis is true. We know that the hypothesis-testing process will lead to this conclusion incorrectly (Type I error) only 100 % of the time when H 0 is true. © 2011 Pearson Education, Inc

Elements of a Test of Hypothesis 7. Conclusion: b. If the test statistic does not fall in the rejection region, we do not reject H 0. Thus, we reserve judgment about which hypothesis is true. We do not conclude that the null hypothesis is true because we do not (in general) know the probability that our test procedure will lead to an incorrect acceptance of H 0 (Type II error). © 2011 Pearson Education, Inc

Determining the Target Parameter Key Words or Phrases µ Mean; average p Proportion; percentage; fraction; rate 2 Variance; variability; spread © 2011 Pearson Education, Inc Type of Data Quantitative Qualitative Quantitative

6. 2 Formulating Hypotheses and Setting Up the Rejection Region © 2011 Pearson Education,

Steps for Selecting the Null and Alternative Hypotheses 1. Select the alternative hypothesis as that which the sampling experiment is intended to establish. The alternative hypothesis will assume one of three forms: a. One-tailed, upper-tailed (e. g. , Ha: µ > 2, 400) b. One-tailed, lower-tailed (e. g. , Ha: µ < 2, 400) c. Two-tailed (e. g. , Ha: µ ≠ 2, 400) © 2011 Pearson Education, Inc

Steps for Selecting the Null and Alternative Hypotheses 2. Select the null hypothesis as the status quo, that which will be presumed true unless the sampling experiment conclusively establishes the alternative hypothesis. The null hypothesis will be specified as that parameter value closest to the alternative in onetailed tests and as the complementary (or only unspecified) value in two-tailed tests. (e. g. , H 0: µ = 2, 400) © 2011 Pearson Education, Inc

One-Tailed Test A one-tailed test of hypothesis is one in which the alternative hypothesis

Two-Tailed Test A two-tailed test of hypothesis is one in which the alternative hypothesis does not specify departure from H 0 in a particular direction and is written with the symbol “ ≠. ” © 2011 Pearson Education, Inc

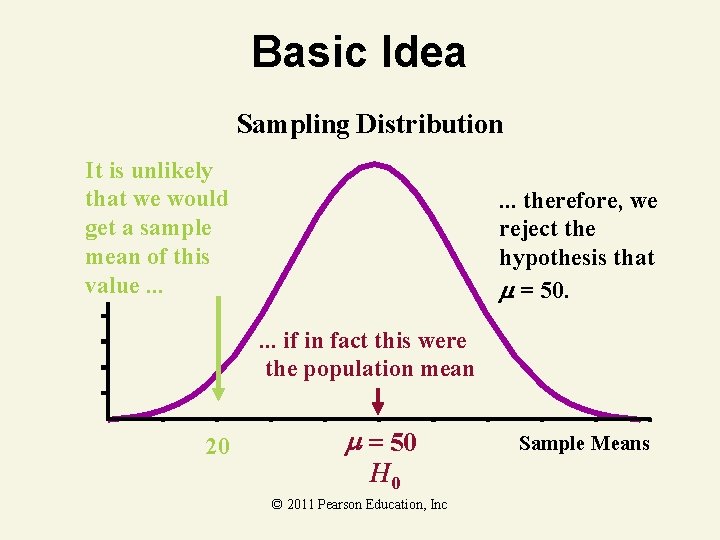
Basic Idea Sampling Distribution It is unlikely that we would get a sample mean of this value. . . therefore, we reject the hypothesis that = 50. . if in fact this were the population mean 20 = 50 H 0 © 2011 Pearson Education, Inc Sample Means

Rejection Region (One-Tail Test) Sampling Distribution Level of Confidence Rejection Region 1– Fail to

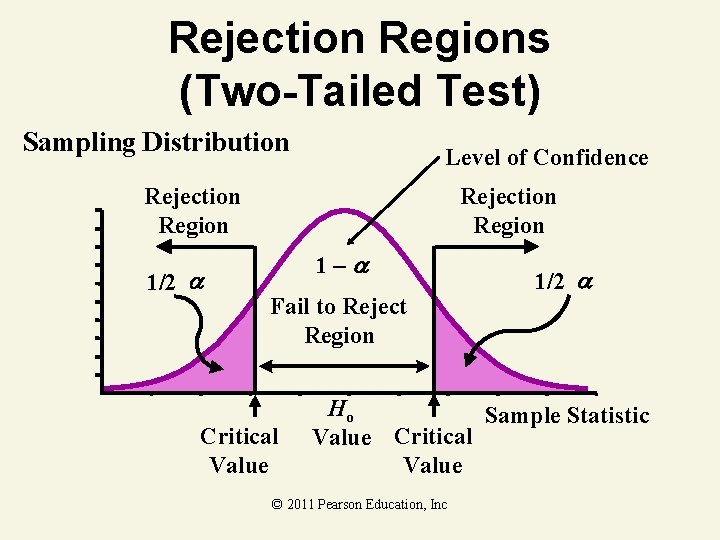
Rejection Regions (Two-Tailed Test) Sampling Distribution Level of Confidence Rejection Region 1/2 Rejection Region 1– Fail to Reject Region Critical Value 1/2 Ho Sample Statistic Value Critical Value © 2011 Pearson Education, Inc

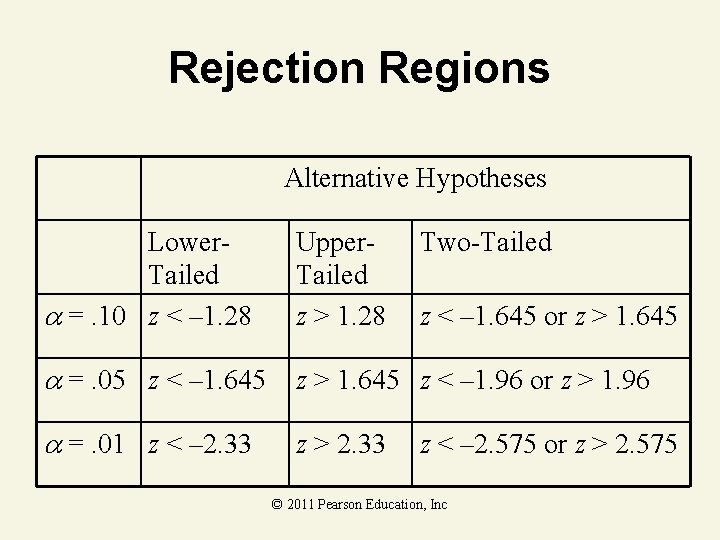
Rejection Regions Alternative Hypotheses Lower. Tailed =. 10 z < – 1. 28 Upper. Tailed z > 1. 28 Two-Tailed =. 05 z < – 1. 645 z > 1. 645 z < – 1. 96 or z > 1. 96 =. 01 z < – 2. 33 z > 2. 33 z < – 1. 645 or z > 1. 645 z < – 2. 575 or z > 2. 575 © 2011 Pearson Education, Inc

6. 3 Test of Hypotheses about a Population Mean: Normal (z) Statistic © 2011

Large-Sample Test of Hypothesis about µ One-Tailed Test Two-Tailed Test H 0: µ =

Large-Sample Test of Hypothesis about µ One-Tailed Test Rejection region: z < –z (or

Large-Sample Test of Hypothesis about µ Two-Tailed Test Rejection region: |z| > z where z is chosen so that P(|z| > z ) = /2 Note: µ 0 is the symbol for the numerical value assigned to µ under the null hypothesis. © 2011 Pearson Education, Inc

Conditions Required for a Valid Large-Sample Hypothesis Test for µ 1. A random sample is selected from the target population. 2. The sample size n is large (i. e. , n ≥ 30). (Due to the Central Limit Theorem, this condition guarantees that the test statistic will be approximately normal regardless of the shape of the underlying probability distribution of the population. ) © 2011 Pearson Education, Inc

Possible Conclusions for a Test of Hypothesis 1. If the calculated test statistic falls in the rejection region, reject H 0 and conclude that the alternative hypothesis Ha is true. State that you are rejecting H 0 at the level of significance. Remember that the confidence is in the testing process, not the particular result of a single test. © 2011 Pearson Education, Inc

Possible Conclusions for a Test of Hypothesis 2. If the test statistic does not fall in the rejection region, conclude that the sampling experiment does not provide sufficient evidence to reject H 0 at the level of significance. [Generally, we will not “accept” the null hypothesis unless the probability of a Type II error has been calculated. ] © 2011 Pearson Education, Inc

Two-Tailed z Test Example Does an average box of cereal contain 368 grams of cereal? A random sample of 25 boxes had x = 372. 5. The company has specified to be 25 grams. Test at the. 05 level of significance. 368 gm. © 2011 Pearson Education, Inc

Two-Tailed z Test Solution • • • H 0: = 368 Ha: 368 . 05 n 25 Critical Value(s): Reject H 0. 025 – 1. 96 Reject H 0. 025 0 1. 96 z Test Statistic: Decision: Do not reject at =. 05 Conclusion: No evidence average is not 368 © 2011 Pearson Education, Inc

Two-Tailed z Test Thinking Challenge You’re a Q/C inspector. You want to find out if a new machine is making electrical cords to customer specification: average breaking strength of 70 lb. with = 3. 5 lb. You take a sample of 36 cords & compute a sample mean of 69. 7 lb. At the. 05 level of significance, is there evidence that the machine is not meeting the average breaking strength? © 2011 Pearson Education, Inc

Two-Tailed z Test Solution* • • • H 0: = 70 Ha: 70 =. 05 n = 36 Critical Value(s): Reject H 0 . 025 – 1. 96 0 1. 96 z Test Statistic: Decision: Do not reject at =. 05 Conclusion: No evidence average is not 70 © 2011 Pearson Education, Inc

One-Tailed z Test Example Does an average box of cereal contain more than 368 grams of cereal? A random sample of 25 boxes showed x = 372. 5. The company has specified to be 25 grams. Test at the. 05 level of significance. 368 gm. © 2011 Pearson Education, Inc

One-Tailed z Test Solution • • • H 0: = 368 Ha: > 368 =. 05 n = 25 Critical Value(s): Reject. 05 0 1. 645 z Test Statistic: Decision: Do not reject at =. 05 Conclusion: No evidence average is more than 368 © 2011 Pearson Education, Inc

One-Tailed z Test Thinking Challenge You’re an analyst for Ford. You want to find out if the average miles per gallon of Escorts is at least 32 mpg. Similar models have a standard deviation of 3. 8 mpg. You take a sample of 60 Escorts & compute a sample mean of 30. 7 mpg. At the. 01 level of significance, is there evidence that the miles per gallon is less than 32? © 2011 Pearson Education, Inc

One-Tailed z Test Solution* • • • H 0: = 32 Ha: < 32 =. 01 n = 60 Critical Value(s): Reject. 01 -2. 33 0 z Test Statistic: Decision: Reject at =. 01 Conclusion: There is evidence average is less than 32 © 2011 Pearson Education, Inc

6. 4 Observed Significance Levels: p-Values © 2011 Pearson Education, Inc

p-Value The observed significance level, or p-value, for a specific statistical test is the probability (assuming H 0 is true) of observing a value of the test statistic that is at least as contradictory to the null hypothesis, and supportive of the alternative hypothesis, as the actual one computed from the sample data. © 2011 Pearson Education, Inc

p-Value • • Probability of obtaining a test statistic more extreme ( or than actual sample value, given H 0 is true Called observed level of significance • • Smallest value of for which H 0 can be rejected Used to make rejection decision • • If p-value , do not reject H 0 If p-value < , reject H 0 © 2011 Pearson Education, Inc

Steps for Calculating the p. Value for a Test of Hypothesis 1. Determine the

Steps for Calculating the p. Value for a Test of Hypothesis 2 a. If the test is one-tailed, the p-value is equal to the tail area beyond z in the same direction as the alternative hypothesis. Thus, if the alternative hypothesis is of the form > , the p-value is the area to the right of, or above, the observed z-value. Conversely, if the alternative is of the form < , the p-value is the area to the left of, or below, the observed z-value. © 2011 Pearson Education, Inc

Steps for Calculating the p. Value for a Test of Hypothesis 2 b. If the test is two-tailed, the p-value is equal to twice the tail area beyond the observed z-value in the direction of the sign of z – that is, if z is positive, the p-value is twice the area to the right of, or above, the observed z-value. Conversely, if z is negative, the p-value is twice the area to the left of, or below, the observed z-value. © 2011 Pearson Education, Inc

Reporting Test Results as p-Values: How to Decide Whether to Reject H 0 1. Choose the maximum value of that you are willing to tolerate. 2. If the observed significance level (p-value) of the test is less than the chosen value of , reject the null hypothesis. Otherwise, do not reject the null hypothesis. © 2011 Pearson Education, Inc

Two-Tailed z Test p-Value Example Does an average box of cereal contain 368 grams of cereal? A random sample of 25 boxes showed x = 372. 5. The company has specified to be 15 grams. Find the p-Value. 368 gm. © 2011 Pearson Education, Inc

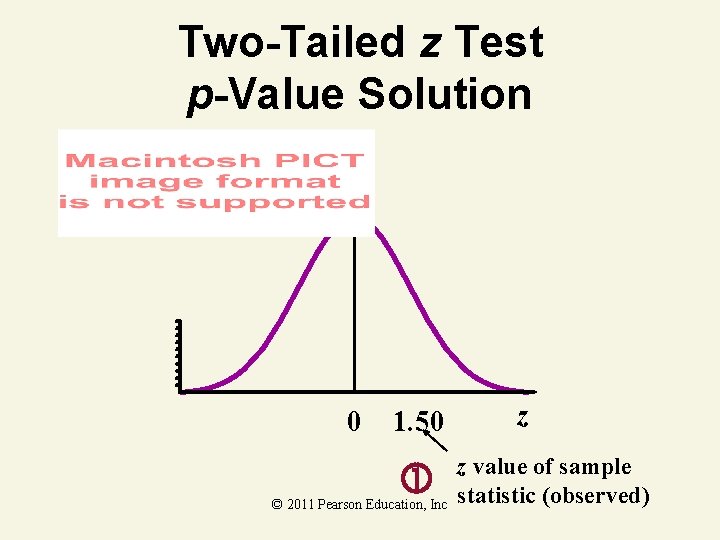
Two-Tailed z Test p-Value Solution 0 1. 50 © 2011 Pearson Education, Inc z

Two-Tailed Z Test p-Value Solution p-value is P(z – 1. 50 or z 1. 50) 1/2 p-Value. 4332 – 1. 50 0 1. 50 . 5000 –. 4332. 0668 z z value of sample From z table: lookup 1. 50 © 2011 Pearson Education, Inc statistic (observed)

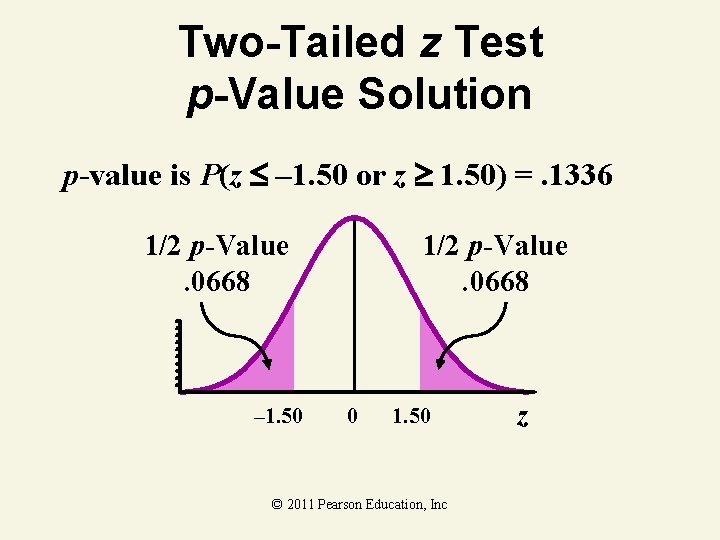
Two-Tailed z Test p-Value Solution p-Value =. 1336 =. 05 Do not reject H 0. 1/2 p-Value =. 0668 Reject H 0 1/2 =. 025 – 1. 50 0 1. 50 Test statistic is in ‘Do not reject’ region © 2011 Pearson Education, Inc z

One-Tailed z Test p-Value Example Does an average box of cereal contain more than 368 grams of cereal? A random sample of 25 boxes showed x = 372. 5. The company has specified to be 15 grams. Find the p. Value. 368 gm. © 2011 Pearson Education, Inc

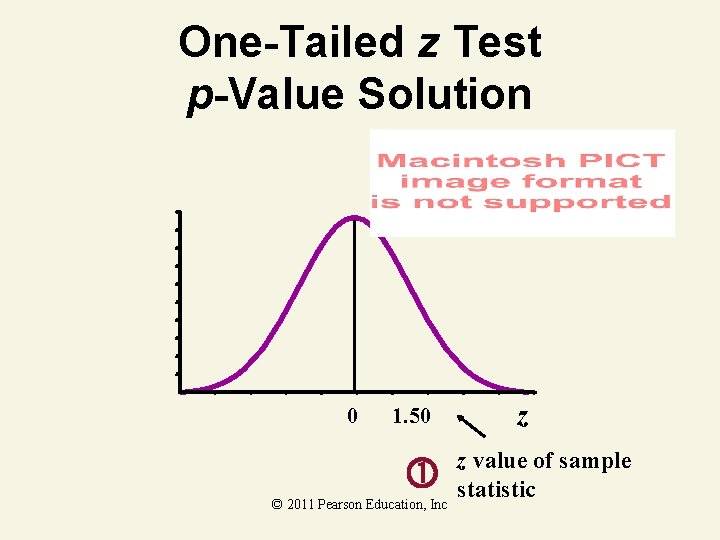
One-Tailed z Test p-Value Solution 0 1. 50 © 2011 Pearson Education, Inc z

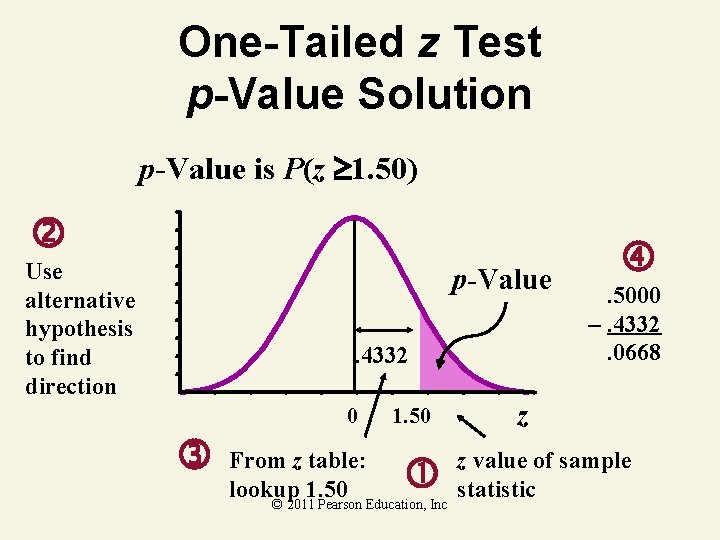
One-Tailed z Test p-Value Solution p-Value is P(z 1. 50) Use alternative hypothesis to find direction p-Value. 4332 0 From z table: lookup 1. 50 © 2011 Pearson Education, Inc . 5000 –. 4332. 0668 z z value of sample statistic

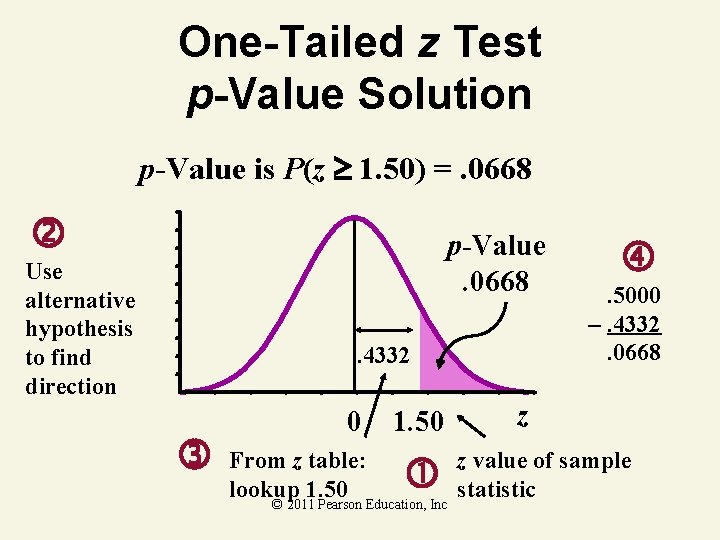
One-Tailed z Test p-Value Solution p-Value is P(z 1. 50) =. 0668 p-Value. 0668 Use alternative hypothesis to find direction . 4332 0 From z table: lookup 1. 50 © 2011 Pearson Education, Inc . 5000 –. 4332. 0668 z z value of sample statistic

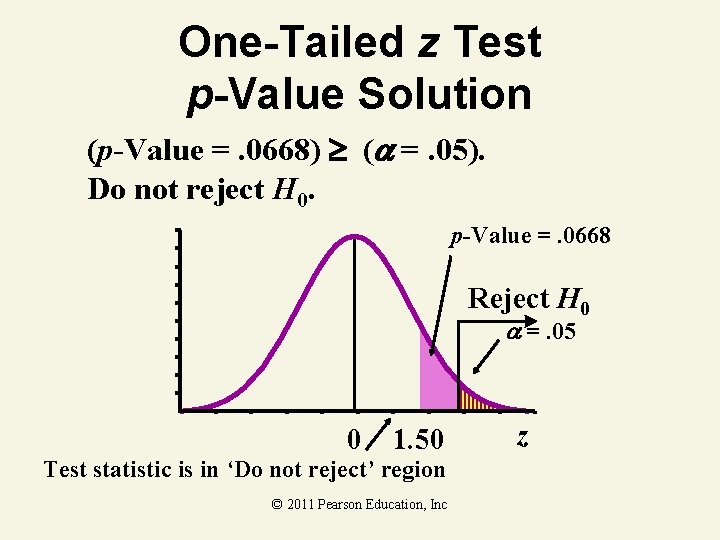
One-Tailed z Test p-Value Solution (p-Value =. 0668) ( =. 05). Do not reject

p-Value Thinking Challenge You’re an analyst for Ford. You want to find out if the average miles per gallon of Escorts is less than 32 mpg. Similar models have a standard deviation of 3. 8 mpg. You take a sample of 60 Escorts & compute a sample mean of 30. 7 mpg. What is the value of the observed level of significance (p-Value)? © 2011 Pearson Education, Inc

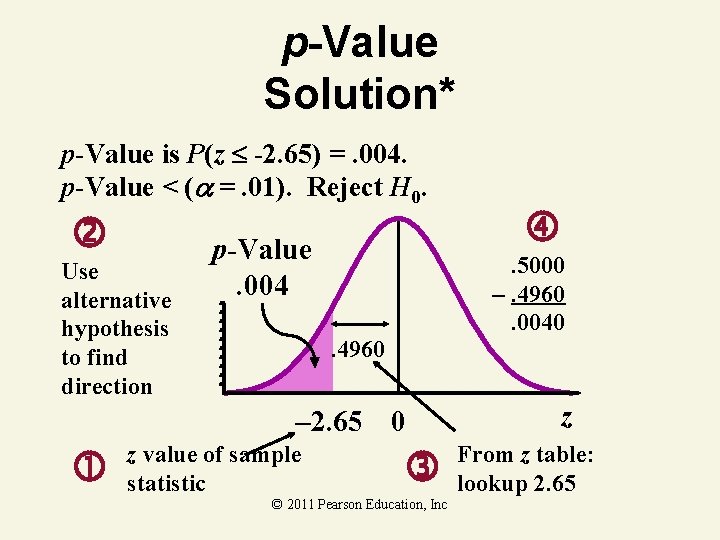
p-Value Solution* p-Value is P(z -2. 65) =. 004. p-Value < ( =. 01). Reject H 0. Use alternative hypothesis to find direction p-Value. 004 . 5000 –. 4960. 0040 . 4960 – 2. 65 0 z value of sample statistic © 2011 Pearson Education, Inc z From z table: lookup 2. 65

Converting a Two-Tailed p-Value from a Printout to a One-Tailed p-Value if Ha is of the form > and z is positive or Ha is of the form < and z is negative if Ha is of the form > and z is negative © 2011 Pearson Education, Inc Ha is of the form < and z is positive

6. 5 Test of Hypothesis about a Population Mean: Student’s t-Statistic © 2011 Pearson

Small-Sample Test of Hypothesis about µ One-Tailed Test H 0: µ = µ 0 Ha: µ < µ 0 (or Ha: µ > µ 0) Test statistic: Rejection region: t < –t (or t > t when Ha: µ > µ 0) where t and t are based on (n – 1) degrees of freedom © 2011 Pearson Education, Inc

Small-Sample Test of Hypothesis about µ Two-Tailed Test H 0: µ = µ 0

Conditions Required for a Valid Small-Sample Hypothesis Test for µ 1. A random sample is selected from the target population. 2. The population from which the sample is selected has a distribution that is approximately normal. © 2011 Pearson Education, Inc

Two-Tailed t Test Example Does an average box of cereal contain 368 grams of cereal? A random sample of 36 boxes had a mean of 372. 5 and a standard deviation of 12 grams. Test at the. 05 level of significance. © 2011 Pearson Education, Inc 368 gm.

Two-Tailed t Test Solution • • • H 0: = 368 Ha: 368 =. 05 df = 36 – 1 = 35 Critical Value(s): Reject H 0 . 025 -2. 030 0 2. 030 t Test Statistic: Decision: Reject at =. 05 Conclusion: There is evidence population average is not 368 © 2011 Pearson Education, Inc

Two-Tailed t Test Thinking Challenge You work for the FTC. A manufacturer of detergent claims that the mean weight of detergent is 3. 25 lb. You take a random sample of 64 containers. You calculate the sample average to be 3. 238 lb. with a standard deviation of. 117 lb. At the. 01 level of significance, is the manufacturer correct? © 2011 Pearson Education, Inc 3. 25 lb.

Two-Tailed t Test Solution* • • • H 0: = 3. 25 Ha: 3. 25 . 01 df 64 – 1 = 63 Critical Value(s): Reject H 0 . 005 -2. 656 0 2. 656 t Test Statistic: Decision: Do not reject at =. 01 Conclusion: There is no evidence average is not 3. 25 © 2011 Pearson Education, Inc

One-Tailed t Test Example Is the average capacity of batteries less than 140 amperehours? A random sample of 20 batteries had a mean of 138. 47 and a standard deviation of 2. 66. Assume a normal distribution. Test at the. 05 level of significance. © 2011 Pearson Education, Inc

One-Tailed t Test Solution • • • H 0: = 140 Ha: < 140 =. 05 df = 20 – 1 = 19 Critical Value(s): Reject H 0 . 05 -1. 729 0 t Test Statistic: Decision: Reject at =. 05 Conclusion: There is evidence population average is less than 140 © 2011 Pearson Education, Inc

One-Tailed t Test Thinking Challenge You’re a marketing analyst for Wal. Mart. Wal-Mart had teddy bears on sale last week. The weekly sales ($ 00) of bears sold in 10 stores was: 8 11 0 4 7 8 10 5 8 3 At the. 05 level of significance, is there evidence that the average bear sales per store is more than 5 ($ 00)? © 2011 Pearson Education, Inc

One-Tailed t Test Solution* • • • H 0: = 5 Ha: > 5 =. 05 df = 10 – 1 = 9 Critical Value(s): Reject H 0. 05 0 1. 833 t Test Statistic: Decision: Do not reject at =. 05 Conclusion: There is no evidence average is more than 5 © 2011 Pearson Education, Inc

6. 6 Large-Sample Test of Hypothesis about a Population Proportion © 2011 Pearson Education,

Large-Sample Test of Hypothesis about p One-Tailed Test H 0: p = p 0 Ha: p < p 0 (or Ha: p > p 0) Test statistic: Rejection region: z < –z (or z > z when Ha: p > p 0) Note: p 0 is the symbol for the numerical value of p assigned in the null hypothesis © 2011 Pearson Education, Inc

Large-Sample Test of Hypothesis about p Two-Tailed Test H 0: p = p 0 Ha: p ≠ p 0 Test statistic: Rejection region: |z| < z Note: p 0 is the symbol for the numerical value of p assigned in the null hypothesis © 2011 Pearson Education, Inc

Conditions Required for a Valid Large-Sample Hypothesis Test for p 1. A random sample is selected from a binomial population. 2. The sample size n is large. (This condition will be satisfied if both np 0 ≥ 15 and nq 0 ≥ 15. ) © 2011 Pearson Education, Inc

One-Proportion z Test Example The present packaging system produces 10% defective cereal boxes. Using a new system, a random sample of 200 boxes had 11 defects. Does the new system produce fewer defects? Test at the. 05 level of significance. © 2011 Pearson Education, Inc

One-Proportion z Test Solution • • • H 0: p =. 10 Ha: p <. 10 =. 05 n = 200 Critical Value(s): Reject H 0 . 05 -1. 645 0 Test Statistic: Decision: Reject at =. 05 Conclusion: There is evidence new z system < 10% defective © 2011 Pearson Education, Inc

One-Proportion z Test Thinking Challenge You’re an accounting manager. A year-end audit showed 4% of transactions had errors. You implement new procedures. A random sample of 500 transactions had 25 errors. Has the proportion of incorrect transactions changed at the. 05 level of significance? © 2011 Pearson Education, Inc

One-Proportion z Test Solution* • • • H 0: p =. 04 Ha: p . 04 =. 05 n = 500 Critical Value(s): Reject H 0 . 025 -1. 96 0 1. 96 z Test Statistic: Decision: Do not reject at =. 05 Conclusion: There is evidence proportion is not 4% © 2011 Pearson Education, Inc

6. 7 Calculating Type II Error Probabilities: More about © 2011 Pearson Education, Inc

Type II Error The Type II error probability is calculated assuming that the null hypothesis is false because it is defined as the probability of accepting H 0 when it is false. The situation corresponding to accepting the null hypothesis, and thereby risking a Type II error, is not generally as controllable. For that reason, we adopted a policy of nonrejection of H 0 when the test statistic does not fall in the rejection region, rather than risking an error of unknown magnitude. © 2011 Pearson Education, Inc

Steps for Calculating for a Large-Sample Test about µ 1. Calculate the value(s) of corresponding to the border(s) of the rejection region. There will be one border value for a one-tailed test and two for a two-tailed test. The formula is one of the following, corresponding to a test with level of significance : Upper-tailed test: © 2011 Pearson Education, Inc

Steps for Calculating for a Large-Sample Test about µ Lower-tailed test: Two-tailed test: ©

Steps for Calculating for a Large-Sample Test about µ 2. Specify the value of µa in the alternative hypothesis for which the value of is to be calculated. Then convert the border value(s) of to z-value(s) using the alternative distribution with mean µa. The general formula for the zvalue is © 2011 Pearson Education, Inc

Steps for Calculating for a Large-Sample Test about µ Sketch the alternative distribution (centered at µa) and shade the area in the acceptance (nonrejection) region. Use the z-statistic(s) and Table IV in Appendix B to find the shaded area, which is . © 2011 Pearson Education, Inc

Power of Test • Probability of rejecting false H 0 • Correct decision • Equal to 1 – • Used in determining test adequacy • Affected by • • • True value of population parameter Significance level Standard deviation & sample size n © 2011 Pearson Education, Inc

Two-Tailed z Test Example Does an average box of cereal contain 368 grams of cereal? A random sample of 25 boxes had x = 372. 5. The company has specified to be 15 grams. Test at the. 05 level of significance. 368 gm. © 2011 Pearson Education, Inc

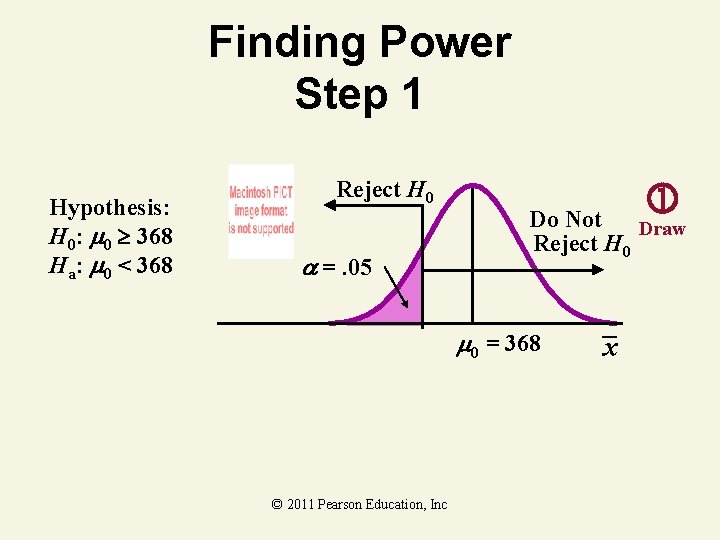
Finding Power Step 1 Hypothesis: H 0: 0 368 Ha: 0 < 368 Reject

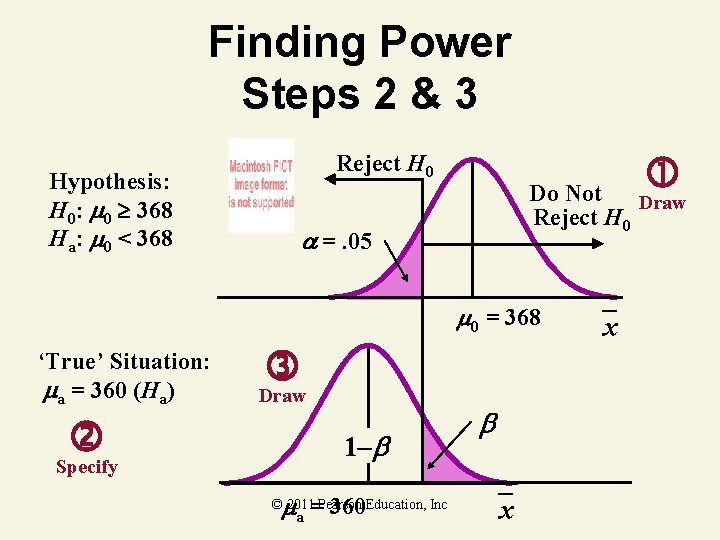
Finding Power Steps 2 & 3 Reject H 0 Hypothesis: H 0: 0 368

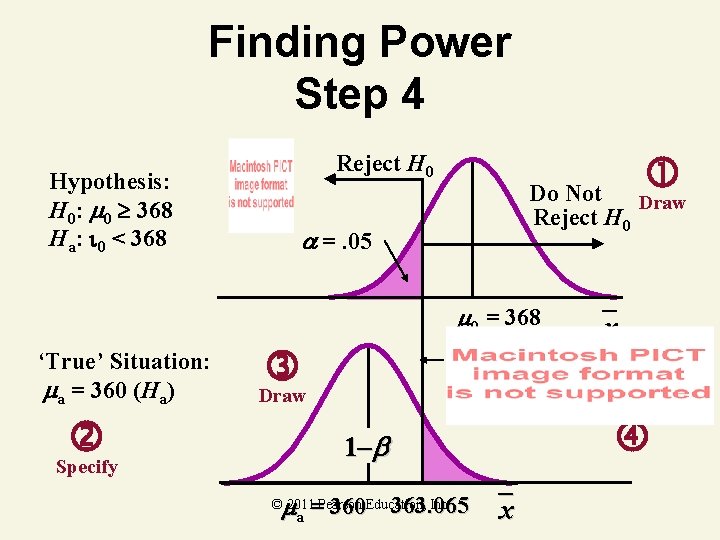
Finding Power Step 4 Reject H 0 Hypothesis: H 0: 0 368 Ha: 0 < 368 Do Not Draw Reject H 0 =. 05 0 = 368 ‘True’ Situation: a = 360 (Ha) Specify x Draw 1– a = 360 363. 065 x © 2011 Pearson Education, Inc

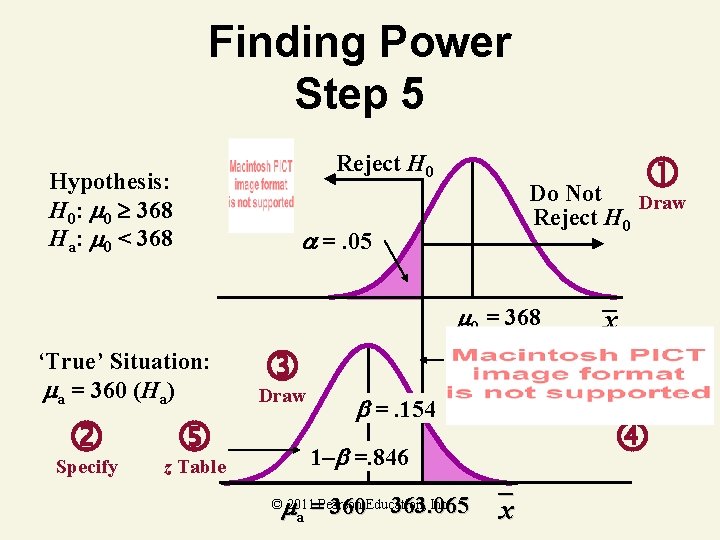
Finding Power Step 5 Reject H 0 Hypothesis: H 0: 0 368 Ha: 0 < 368 Do Not Draw Reject H 0 =. 05 0 = 368 ‘True’ Situation: a = 360 (Ha) Specify z Table x Draw =. 154 1– =. 846 a = 360 363. 065 x © 2011 Pearson Education, Inc

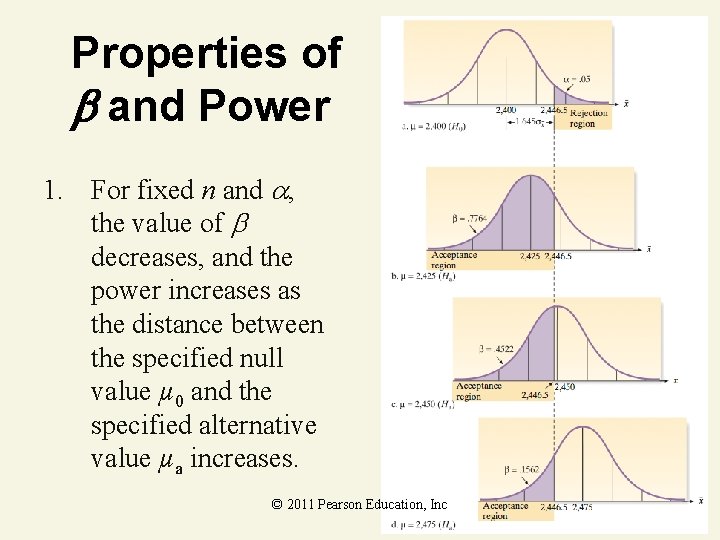
Properties of and Power 1. For fixed n and , the value of decreases, and the power increases as the distance between the specified null value µ 0 and the specified alternative value µa increases. © 2011 Pearson Education, Inc

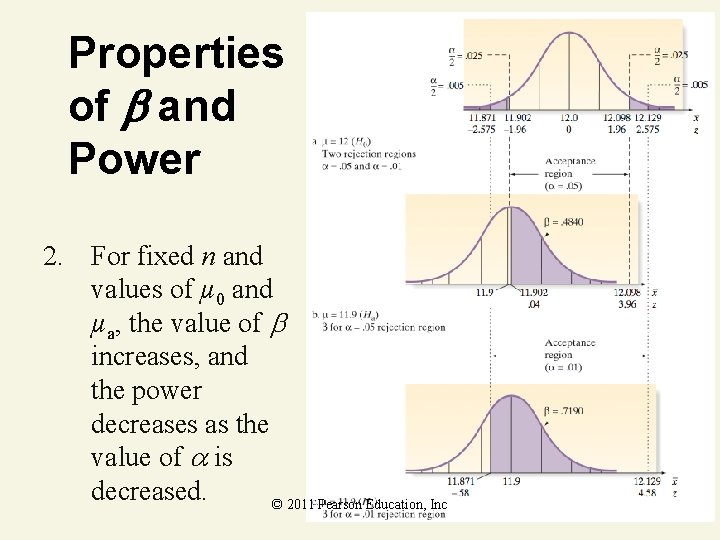
Properties of and Power 2. For fixed n and values of µ 0 and

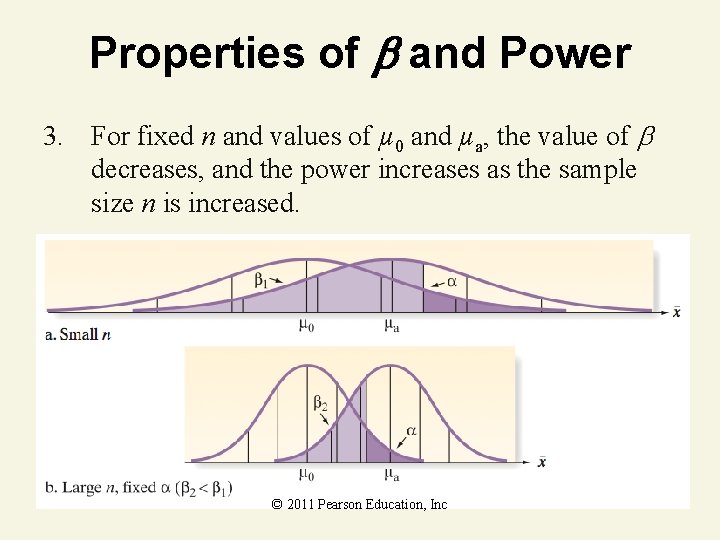
Properties of and Power 3. For fixed n and values of µ 0 and

6. 8 Test of Hypothesis about a Population Variance © 2011 Pearson Education, Inc

Variance Although many practical problems involve inferences about a population mean (or proportion), it is sometimes of interest to make an inference about a population variance, 2. © 2011 Pearson Education, Inc

Test of a Hypothesis about 2 One-Tailed Test H 0: = 0 Ha: < 0 (or Ha: > 0 ) Test statistic: Rejection region: (or > when Ha: > 0 ) where 0 is the hypothesized variance and the distribution of is based on (n – 1) degrees of freedom. © 2011 Pearson Education, Inc

Test of a Hypothesis about 2 Two-Tailed Test H 0: = 0 Ha: ≠ 0 Test statistic: Rejection region: where 0 is the hypothesized variance and the distribution of is based on (n – 1) degrees of freedom. © 2011 Pearson Education, Inc

Conditions Required for a Valid Hypothesis Test for s 2 1. A random sample is selected from the target population. 2. The population from which the sample is selected has a distribution that is approximately normal. © 2011 Pearson Education, Inc

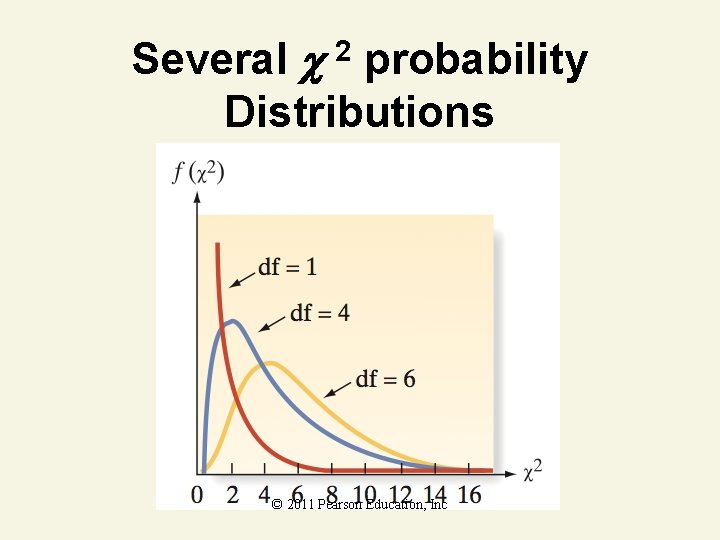
Several 2 probability Distributions © 2011 Pearson Education, Inc

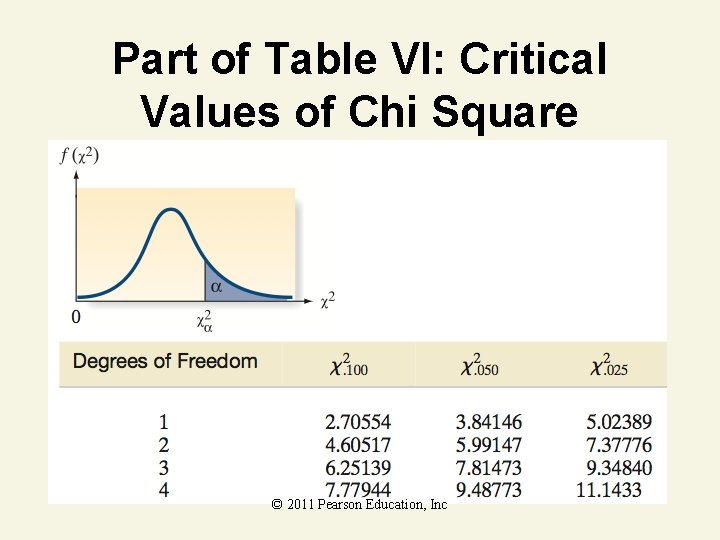
Part of Table VI: Critical Values of Chi Square © 2011 Pearson Education, Inc

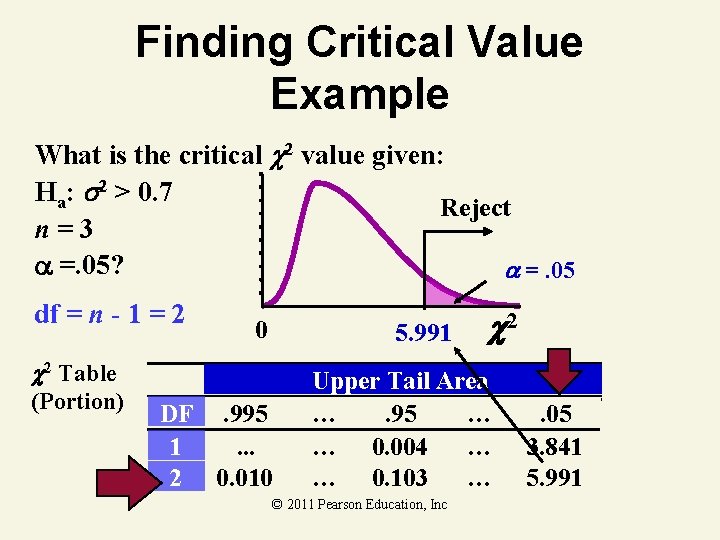
Finding Critical Value Example What is the critical 2 value given: Ha: 2 > 0. 7 Reject n=3 =. 05? =. 05 df = n - 1 = 2 0 5. 991 2 Table (Portion) DF. 995 1. . . 2 0. 010 2 Upper Tail Area …. 95 … … 0. 004 … … 0. 103 … © 2011 Pearson Education, Inc . 05 3. 841 5. 991

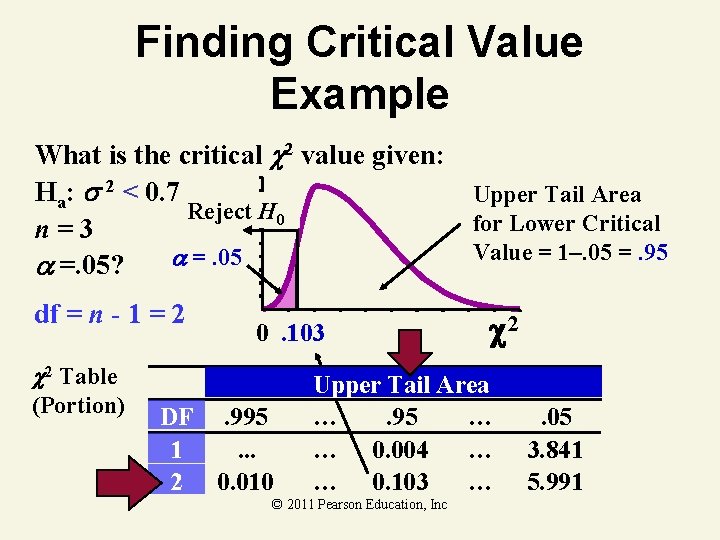
Finding Critical Value Example What is the critical 2 value given: Ha: 2 < 0. 7 Upper Tail Area Reject H 0 for Lower Critical n=3 Value = 1–. 05 =. 95 =. 05? df = n - 1 = 2 0. 103 2 Table (Portion) DF. 995 1. . . 2 0. 010 c 2 Upper Tail Area …. 95 … … 0. 004 … … 0. 103 … © 2011 Pearson Education, Inc . 05 3. 841 5. 991

Chi-Square ( 2) Test Example Is the variation in boxes of cereal, measured by the variance, equal to 15 grams? A random sample of 25 boxes had a standard deviation of 17. 7 grams. Test at the. 05 level of significance. © 2011 Pearson Education, Inc

Chi-Square ( Test Solution 2) • • • H 0: 2 = 15 Ha: 2 15 =. 05 df = 25 – 1 = 24 Critical Value(s): /2 =. 025 Test Statistic: = 33. 42 Decision: Do not reject at =. 05 Conclusion: There is no evidence 2 2 is not 15 0 12. 401 39. 364 © 2011 Pearson Education, Inc

Key Ideas Key Words for Identifying the Target Parameter – Mean, Average p –

Key Ideas Elements of a Hypothesis Test 1. Null hypothesis (H 0) 2. Alternative hypothesis (Ha) 3. Test statistic (z, t, or 2) 4. Significance level ( ) 5. p-value 6. Conclusion © 2011 Pearson Education, Inc

Key Ideas Errors in Hypothesis Testing Type I Error = Reject H 0 when H 0 is true (occurs with probability ) Type II Error = Accept H 0 when H 0 is false (occurs with probability ) Power of Test = P(Reject H 0 when H 0 is false) =1– © 2011 Pearson Education, Inc