2011 Pearson Education Inc Statistics for Business and

© 2011 Pearson Education, Inc

Statistics for Business and Economics Chapter 14 Nonparametric Statistics © 2011 Pearson Education, Inc

Content 14. 1 Introduction: Distribution-Free Tests 14. 2 Single Population Inferences 14. 3 Comparing Two Populations: Independent Samples 14. 4 Comparing Two Populations: Paired Difference Experiment 14. 5 Comparing Three or More Populations: Completely Randomized Design © 2011 Pearson Education, Inc

Content 14. 6 Comparing Three or More Populations: Randomized Block Design 14. 7 Rank Correlation © 2011 Pearson Education, Inc

Learning Objectives • • Develop the need for inferential techniques that require fewer, or less stringent, assumptions than the methods of earlier chapters Introduce nonparametric tests that are based on ranks (i. e. , on an ordering of the sample measurements according to their relative magnitudes) © 2011 Pearson Education, Inc

14. 1 Introduction: Distribution-Free Tests © 2011 Pearson Education, Inc

Parametric Test Procedures • Involve population parameters — Example: population mean • Require interval scale or ratio scale — Whole numbers or fractions — Example: height in inches (72, 60. 5, 54. 7) • Have stringent assumptions — Example: normal distribution • Examples: z-test, t-test, F-test, 2 -test © 2011 Pearson Education, Inc

Nonparametric Test Procedures • Do not involve population parameters — Example: probability distributions, independence • Data measured on any scale — Ratio or interval — Ordinal § Example: good-better-best — Nominal § Example: male-female • Example: Wilcoxon rank sum test © 2011 Pearson Education, Inc

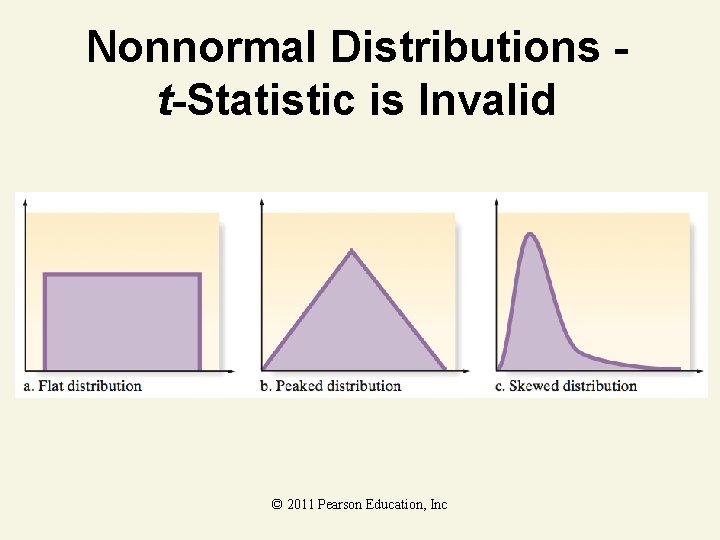
Nonnormal Distributions t-Statistic is Invalid © 2011 Pearson Education, Inc

Distribution-Free Tests Distribution-free tests are statistical tests that do not rely on any underlying assumptions about the probability distribution of the sampled population. The branch of inferential statistics devoted to distribution-free tests is called nonparametrics. Nonparametric statistics (or tests) based on the ranks of measurements are called rank statistics (or rank tests). © 2011 Pearson Education, Inc

Advantages of Nonparametric Tests • Used with all scales • Easier to compute — Developed originally before wide computer use • Make fewer assumptions • Need not involve population parameters • Results may be as exact as parametric procedures © 2011 Pearson Education, Inc © 1984 -1994 T/Maker Co.

Disadvantages of Nonparametric Tests • May waste information — If data permit using parametric procedures — Example: converting data from ratio to ordinal scale • Difficult to compute by hand for large samples • Tables not widely available © 2011 Pearson Education, Inc © 1984 -1994 T/Maker Co.

Frequently Used Nonparametric Tests • Sign Test • Wilcoxon Rank Sum Test • Wilcoxon Signed Rank Test • Kruskal Wallis H-Test • Spearman’s Rank Correlation Coefficient © 2011 Pearson Education, Inc

14. 2 Single Population Inferences © 2011 Pearson Education, Inc

Sign Test • • Tests one population median, (eta) Corresponds to t-test for one mean Assumes population is continuous Small sample test statistic: Number of sample values above (or below) median — Alternative hypothesis determines • Can use normal approximation if n 30 © 2011 Pearson Education, Inc

Sign Test Uses p-Value to Make Decision Binomial: n = 8 p = 0. 5 P-value is the probability of getting an observation at least as extreme as we got. If 7 of 8 observations ‘favor’ Ha, then p-value = p(x 7) =. 031 +. 004 =. 035. If =. 05, then reject ©H 2011 Pearson p-value Education, Inc . 0 since

Sign Test for a Population Median One-Tailed Test H 0: = 0 Ha: > 0 [or Ha: < 0 ] Test statistic: S = Number of sample measurements greater than 0 [or S = number of measurements less than 0] © 2011 Pearson Education, Inc

Sign Test for a Population Median Observed significance level: p-value = P(x ≥ S) where x has a binomial distribution with parameters n and p =. 5 (Use Table II, Appendix B) Rejection region: Reject H 0 if p-value ≤. 05 © 2011 Pearson Education, Inc

Sign Test for a Population Median Two-Tailed Test H 0: = 0 H a : ≠ 0 Test statistic: S = Larger of S 1 and S 2, where S 1 is the number of sample measurements less than 0 and S 2 is the number of measurements greater than 0 © 2011 Pearson Education, Inc

Sign Test for a Population Median Observed significance level: p-value = 2 P(x ≥ S) where x has a binomial distribution with parameters n and p =. 5 (Use Table II, Appendix B) Rejection region: Reject H 0 if p-value ≤. 05 © 2011 Pearson Education, Inc

Conditions Required for Valid Application of the Sign Test The sample is selected randomly from a continuous probability distribution. [Note: No assumptions need to be made about the shape of the probability distribution. ] © 2011 Pearson Education, Inc

Large Sample Sign Test for a Population Median One-Tailed Test H 0: = 0 Ha: > 0 [or Ha: < 0 ] Test statistic: S = Number of sample measurements greater than 0 [or S = number of measurements less than 0] The “–. 5” is the “correction for continuity. ” © 2011 Pearson Education, Inc

Large Sample Sign Test for a Population Median The null hypothesized mean value is np =. 5 n, and the standard deviation is Rejection region: z > z where tabulated z-values can be found in Table IV of Appendix B. © 2011 Pearson Education, Inc

Large Sample Sign Test for a Population Median Two-Tailed Test H 0: = 0 H a : ≠ 0 Test statistic: S = Larger of S 1 and S 2, where S 1 is the number of sample measurements less than 0 and S 2 is the number of measurements greater than 0 © 2011 Pearson Education, Inc

Large Sample Sign Test for a Population Median The null hypothesized mean value is np =. 5 n, and the standard deviation is Rejection region: z > z where tabulated z-values can be found in Table IV of Appendix B. © 2011 Pearson Education, Inc

Sign Test Example You’re an analyst for Chef-Boy. R-Dee. You’ve asked 7 people to rate a new ravioli on a 5 -point Likert scale (1 = terrible to 5 = excellent). The ratings are: 2 5 3 4 1 4 5 At the. 05 level of significance, is there evidence that the median rating is less than 3? © 2011 Pearson Education, Inc

Sign Test Solution • • H 0: = 3 Ha: < 3 =. 05 Test Statistic: S=2 (Ratings 1 & 2 are less than = 3: 2, 5, 3, 4, 1, 4, 5) p-value: P(x 2) = 1 – P(x 1) =. 937 (Binomial Table, n = 7, p = 0. 50) Decision: Do not reject at =. 05 Conclusion: There is no evidence median is less than 3 © 2011 Pearson Education, Inc

14. 3 Comparing Two Populations: Independent Samples © 2011 Pearson Education, Inc

Wilcoxon Rank Sum Test • Tests two independent population probability distributions • Corresponds to t-test for two independent means • Assumptions — Independent, random samples — Populations are continuous • Can use normal approximation if ni 10 © 2011 Pearson Education, Inc

Wilcoxon Rank Sum Test: Independent Samples Let D 1 and D 2 represent the probability distributions for populations 1 and 2, respectively. One-Tailed Test H 0: D 1 and D 2 are identical Ha: D 1 is shifted to the right of D 2 [or D 1 is shifted to the left of D 2] Test statistic: T 1, if n 1 < n 2; T 2, if n 2 < n 1 (Either rank sum can be used if n 1 = n 2. ) © 2011 Pearson Education, Inc

Wilcoxon Rank Sum Test: Independent Samples Rejection region: T 1 ≥ TU [or T 1 ≤ TL] T 2: T 2 ≤ TL [or T 2 ≥ TU] where TL and TU are obtained from Table XIV of Appendix B Ties: Assign tied measurements the average of the ranks they would receive if they were unequal but occurred in successive order. For example, if the third-ranked and fourth-ranked measurements are tied, assign each a rank of (3 + 4)/2 = 3. 5 © 2011 Pearson Education, Inc

Wilcoxon Rank Sum Test: Independent Samples Let D 1 and D 2 represent the probability distributions for populations 1 and 2, respectively. Two-Tailed Test H 0: D 1 and D 2 are identical Ha: D 1 is shifted to the left or to the right of D 2 Test statistic: T 1, if n 1 < n 2; T 2, if n 2 < n 1 (Either rank sum can be used if n 1 = n 2. ) We will denote this rank sum as T. © 2011 Pearson Education, Inc

Wilcoxon Rank Sum Test: Independent Samples Rejection region: T ≤ TL or T ≥ TU where TL and TU are obtained from Table XIV of Appendix B Ties: Assign tied measurements the average of the ranks they would receive if they were unequal but occurred in successive order. For example, if the third-ranked and fourth-ranked measurements are tied, assign each a rank of (3 + 4)/2 = 3. 5 © 2011 Pearson Education, Inc

Conditions Required for Valid Wilcoxon Rank Sum Test 1. The two samples are random and independent. 2. The two probability distributions from which the samples are drawn are continuous. © 2011 Pearson Education, Inc

Wilcoxon Rank Sum Test Procedure 1. Assign ranks, Ri, to the n 1 + n 2 sample observations • If unequal sample sizes, let n 1 refer to smallersized sample • Smallest value = 1 • Average ties 2. Sum the ranks, Ti, for each sample 3. Test statistic is Ti (smallest sample) © 2011 Pearson Education, Inc

Wilcoxon Rank Sum Test Example You’re a production planner. You want to see if the operating rates for two factories is the same. For factory 1, the rates (% of capacity) are 85, 82, 94, and 97. For factory 2, the rates are 71, 82, 77, 92, and 88. Do the factory rates have the same probability distributions at the. 10 level of significance? © 2011 Pearson Education, Inc

Wilcoxon Rank Sum Test Solution • • • H 0: Identical Distrib. Ha: Shifted Left or Right =. 10 n 1 = 4 n 25= Critical Value(s): © 2011 Pearson Education, Inc

Wilcoxon Rank Sum Table (Portion) =. 05 one-tailed; =. 10 two-tailed n 1 3 n 2 3 4 5 : TL 6 7 7 : 4 TU TL 15 7 17 12 20 13 : : 5 TU TL 17 7 24 13 27 19 : : © 2011 Pearson Education, Inc TU 20 27 36 : . . :

Wilcoxon Rank Sum Test Solution • • • H 0: Identical Distrib. Ha: Shifted Left or Right =. 10 n 1 = 4 n 2 = 5 Critical Value(s): Reject Do Not Reject H 0 H 0 13 27 Ranks © 2011 Pearson Education, Inc

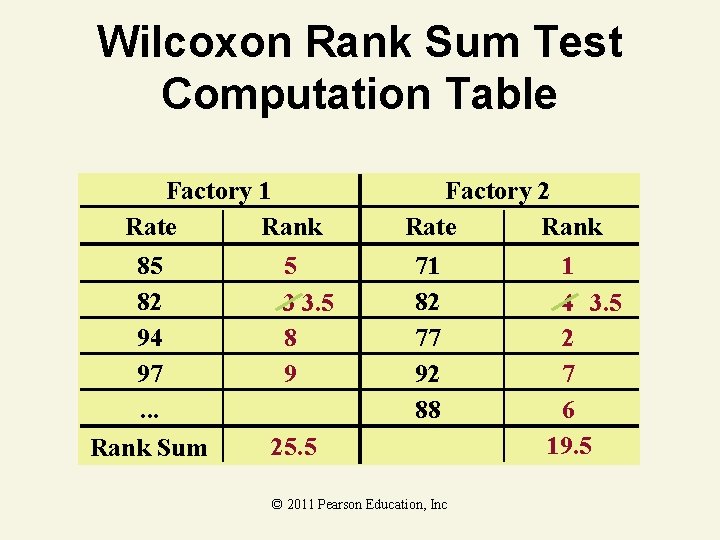
Wilcoxon Rank Sum Test Computation Table Factory 1 Rate Rank 85 5 82 3 3. 5 94 8 97 9. . . 25. 5 Rank Sum Factory 2 Rate Rank 71 1 82 4 3. 5 77 2 92 7 88 6 19. 5 © 2011 Pearson Education, Inc

Wilcoxon Rank Sum Test Solution • • • H 0: Identical Distrib. Test Statistic: Ha: Shifted Left or Right T 1 = 5 + 3. 5 + 8+ 9 = 25. 5 (Smallest sample) =. 10 n 1 = 4 n 2 = 5 Critical Value(s): Decision: Do not reject at =. 10 Reject Do Not Reject H 0 H 0 13 Conclusion: There is no evidence 27 Ranks distrib. are not identical © 2011 Pearson Education, Inc

Wilcoxon Rank Sum Test for Large Samples (n 1 ≥ 10 and n 2 ≥ 10) Let D 1 and D 2 represent the probability distributions for populations 1 and 2, respectively. One-Tailed Test H 0: D 1 and D 2 are identical Ha: D 1 is shifted to the right of D 2 [or D 1 is shifted to the left of D 2] © 2011 Pearson Education, Inc

Wilcoxon Rank Sum Test for Large Samples (n 1 ≥ 10 and n 2 ≥ 10) Test statistic: Rejection region: z > z (or z < –z ) © 2011 Pearson Education, Inc

Wilcoxon Rank Sum Test for Large Samples (n 1 ≥ 10 and n 2 ≥ 10) Let D 1 and D 2 represent the probability distributions for populations 1 and 2, respectively. Two-Tailed Test H 0: D 1 and D 2 are identical Ha: D 1 is shifted to the right or to the left of D 2 © 2011 Pearson Education, Inc

Wilcoxon Rank Sum Test for Large Samples (n 1 ≥ 10 and n 2 ≥ 10) Test statistic: Rejection region: | z | > z /2 © 2011 Pearson Education, Inc

14. 4 Comparing Two Populations: Paired Differences Experiment © 2011 Pearson Education, Inc

Wilcoxon Signed Rank Test • Tests probability distributions of two related populations • Corresponds to t-test for dependent (paired) means • Assumptions — Random samples — Both populations are continuous • Can use normal approximation if n 25 © 2011 Pearson Education, Inc

Wilcoxon Signed Rank Test for a Paired Difference Experiment Let D 1 and D 2 represent the probability distributions for populations 1 and 2, respectively. One-Tailed Test H 0: D 1 and D 2 are identical Ha: D 1 is shifted to the right of D 2 [or D 1 is shifted to the left of D 2] © 2011 Pearson Education, Inc

Wilcoxon Signed Rank Test for a Paired Difference Experiment Calculate the difference within each of the n matched pairs of observations. Then rank the absolute value of the n differences from the smallest (rank 1) to the highest (rank n) and calculate the rank sum T– of the negative differences and the rank sum T+ of the positive differences. [Note: Differences equal to 0 are eliminated, and the number n of differences is reduced accordingly. ] © 2011 Pearson Education, Inc

Wilcoxon Signed Rank Test for a Paired Difference Experiment Test statistic: T–, the rank sum of the negative differences [or T+, the rank sum of the positive differences] Rejection region: T– ≤ T 0 [or T+ ≤ T 0] where T 0 is given in Table XV of Appendix B Ties: Assign tied measurements the average of the ranks they would receive if they were unequal but occurred in successive order. For example, if the third-ranked and fourth-ranked measurements are tied, assign each a rank of (3 + 4)/2 = 3. 5 © 2011 Pearson Education, Inc

Wilcoxon Signed Rank Test for a Paired Difference Experiment Let D 1 and D 2 represent the probability distributions for populations 1 and 2, respectively. Two-Tailed Test H 0: D 1 and D 2 are identical Ha: D 1 is shifted to the left or to the right of D 2 © 2011 Pearson Education, Inc

Wilcoxon Signed Rank Test for a Paired Difference Experiment Calculate the difference within each of the n matched pairs of observations. Then rank the absolute value of the n differences from the smallest (rank 1) to the highest (rank n) and calculate the rank sum T– of the negative differences and the rank sum T+ of the positive differences. [Note: Differences equal to 0 are eliminated, and the number n of differences is reduced accordingly. ] © 2011 Pearson Education, Inc

Wilcoxon Signed Rank Test for a Paired Difference Experiment Test statistic: T–, the rank sum of the negative differences [or T+, the rank sum of the positive differences] Rejection region: T ≤ T 0 where T 0 is given in Table XV of Appendix B Ties: Assign tied measurements the average of the ranks they would receive if they were unequal but occurred in successive order. For example, if the third-ranked and fourth-ranked measurements are tied, assign each a rank of (3 + 4)/2 = 3. 5 © 2011 Pearson Education, Inc

Conditions Required for a Valid Signed Rank Test 1. The sample of differences is randomly selected from the population of differences. 2. The probability distribution from which the sample of paired differences is drawn is continuous. © 2011 Pearson Education, Inc

Signed Rank Test Procedure 1. 2. 3. 4. 5. 6. Obtain difference scores, Di = X 1 i – X 2 i Take absolute value of differences, |Di| Delete differences with 0 value Assign ranks, Ri, where smallest = 1 Assign ranks same signs as Di Sum ‘+’ ranks (T+) and ‘–’ ranks (T–) 1. Test statistic is T– or T+ (one-tail test) 2. Test statistic is T = smaller of T– or T+ (two-tail test) © 2011 Pearson Education, Inc

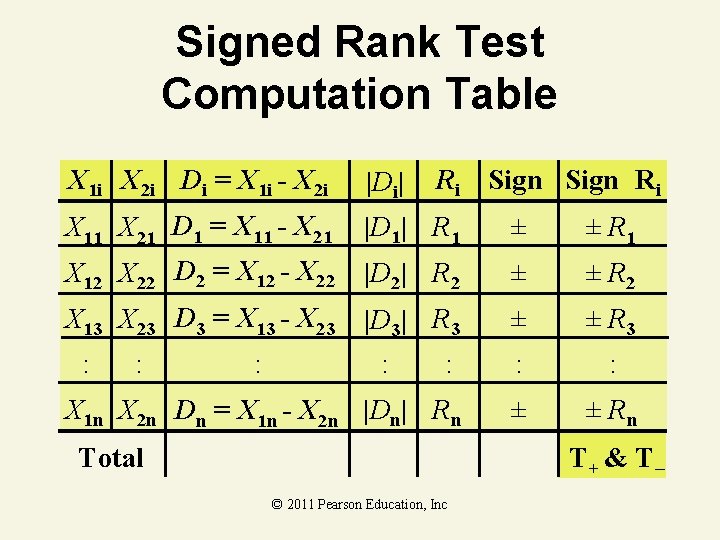
Signed Rank Test Computation Table X 1 i X 2 i Di = X 1 i - X 2 i |Di| X 11 X 21 D 1 = X 11 - X 21 |D 1| R 1 ± ± R 1 X 12 X 22 D 2 = X 12 - X 22 |D 2| R 2 ± ± R 2 X 13 X 23 D 3 = X 13 - X 23 |D 3| R 3 ± ± R 3 : : ± ± Rn : : Ri Sign Ri : X 1 n X 2 n Dn = X 1 n - X 2 n |Dn| Rn Total T+ & T– © 2011 Pearson Education, Inc

Signed Rank Test Example You work in the finance department. Is the new financial package faster (α =. 05)? You collect the following data entry times: User Current New Donna 9. 98 9. 88 Santosha 9. 88 9. 86 Sam 9. 90 9. 83 Tamika 9. 99 9. 80 Brian 9. 94 9. 87 Jorge 9. 84 © 2011 Pearson Education, Inc © 1984 -1994 T/Maker Co.

Signed Rank Test Solution • H 0: Identical Distrib. • Ha: Current Shifted Right • =. 05 • n' = • Critical Value(s): © 2011 Pearson Education, Inc

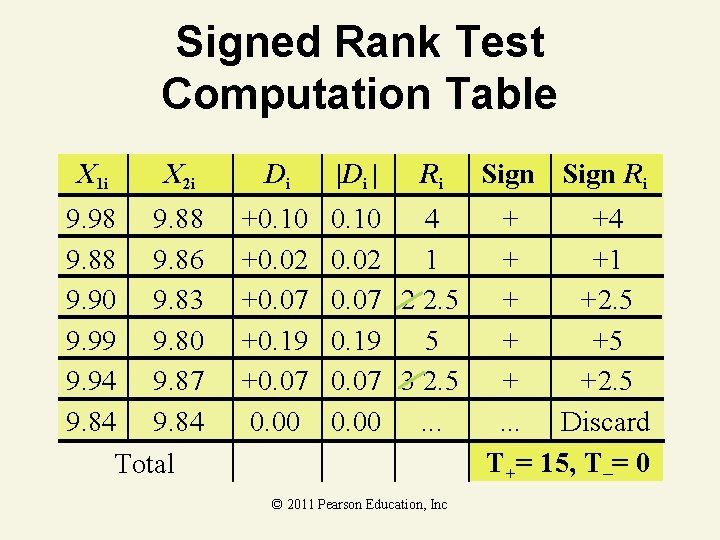
Signed Rank Test Computation Table X 1 i X 2 i 9. 98 9. 88 9. 86 9. 90 9. 83 9. 99 9. 80 9. 94 9. 87 9. 84 Total Di +0. 10 +0. 02 +0. 07 +0. 19 +0. 07 0. 00 |Di | Ri 0. 10 4 0. 02 1 0. 07 2 2. 5 0. 19 5 0. 07 3 2. 5 0. 00. . . © 2011 Pearson Education, Inc Sign Ri + +4 + +1 + +2. 5. . . Discard T+= 15, T–= 0

Signed Rank Test Solution • H 0: Identical Distrib. • Ha: Current Shifted Right • =. 05 • n' = 5 (not 6; 1 elim. ) • Critical Value(s): © 2011 Pearson Education, Inc

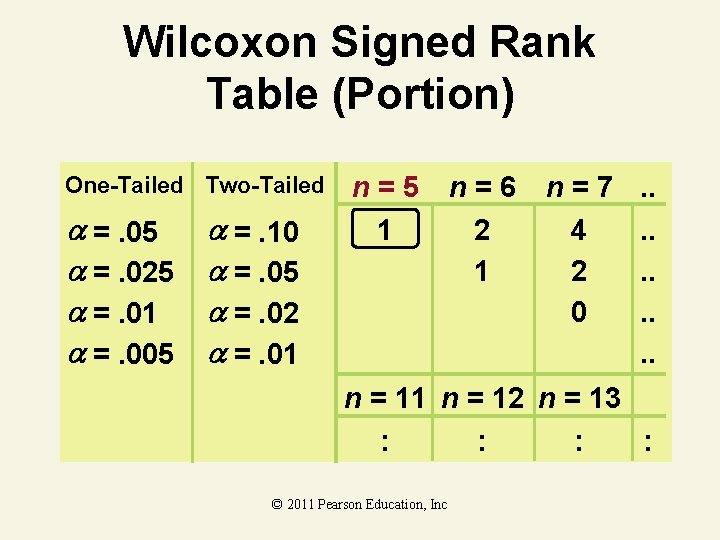
Wilcoxon Signed Rank Table (Portion) One-Tailed Two-Tailed =. 05 =. 025 =. 01 =. 005 =. 10 =. 05 =. 02 =. 01 n=5 1 n=6 2 1 n=7 4 2 0 . . n = 11 n = 12 n = 13 : : © 2011 Pearson Education, Inc

Signed Rank Test Solution • H 0: Identical Distrib. • Ha: Current Shifted Right • =. 05 • n' = 5 (not 6; 1 elim. ) • Critical Value(s): Reject Do Not Reject H 0 1 T 0 Test Statistic: T– = 0 Decision: Reject at =. 05 Conclusion: There is evidence new package is faster © 2011 Pearson Education, Inc

Wilcoxon Signed Rank Test for Large Samples (n ≥ 25) Let D 1 and D 2 represent the probability distributions for populations 1 and 2, respectively. One-Tailed Test H 0: D 1 and D 2 are identical Ha: D 1 is shifted to the right of D 2 [or D 1 is shifted to the left of D 2] © 2011 Pearson Education, Inc

Wilcoxon Signed Rank Test for a Paired Difference Experiment Test statistic: Rejection region: z > z [or z < –z ] © 2011 Pearson Education, Inc

Wilcoxon Signed Rank Test for a Paired Difference Experiment Assumptions: The sample size n is greater than or equal to 25. Differences equal to 0 are eliminated, and the number n of differences is reduced accordingly. Tied absolute differences receive ranks equal to the average of the ranks they would have received had they not been tied. © 2011 Pearson Education, Inc

Wilcoxon Signed Rank Test for Large Samples (n ≥ 25) Let D 1 and D 2 represent the probability distributions for populations 1 and 2, respectively. Two-Tailed Test H 0: D 1 and D 2 are identical Ha: D 1 is shifted to the left or to the right of D 2 © 2011 Pearson Education, Inc

Wilcoxon Signed Rank Test for a Paired Difference Experiment Test statistic: Rejection region: | z | > z © 2011 Pearson Education, Inc

Wilcoxon Signed Rank Test for a Paired Difference Experiment Assumptions: The sample size n is greater than or equal to 25. Differences equal to 0 are eliminated, and the number n of differences is reduced accordingly. Tied absolute differences receive ranks equal to the average of the ranks they would have received had they not been tied. © 2011 Pearson Education, Inc

14. 5 Comparing Three or More Populations: Completely Randomized Design © 2011 Pearson Education, Inc

Kruskal-Wallis H-Test • Tests the equality of more than two (p) population probability distributions • Corresponds to ANOVA for more than two means • Used to analyze completely randomized experimental designs • Uses 2 distribution with p – 1 df — if sample size nj ≥ 5 © 2011 Pearson Education, Inc

Kruskal-Wallis H-Test for Comparing k Probability Distributions H 0: The k probability distributions are identical Ha: At least two of the k probability distributions differ in location. Test statistic: © 2011 Pearson Education, Inc

Kruskal-Wallis H-Test for Comparing k Probability Distributions where nj = Number of measurements in sample j Rj = Rank sum for sample j, where the rank of each measurement is computed according to its relative magnitude in the totality of data for the k samples Rj = Rj/nj = Mean rank sum for jth sample R = Mean of all ranks = (n + 1)/2 n = Total sample size = n 1 + n 2 +. . . + nk © 2011 Pearson Education, Inc

Kruskal-Wallis H-Test for Comparing k Probability Distributions Rejection region: H > with (k – 1) degrees of freedom Ties: Assign tied measurements the average of the ranks they would receive if they were unequal but occurred in successive order. For example, if the third-ranked and fourth-ranked measurements are tied, assign each a rank of (3 + 4)/2 = 3. 5. The number should be small relative to the total number of observations. © 2011 Pearson Education, Inc

Conditions Required for the Validity of the Kruskal-Wallis H-Test 1. The k samples are random and independent. 2. There are five or more measurements in each sample. 3. The k probability distributions from which the samples are drawn are continuous © 2011 Pearson Education, Inc

Kruskal-Wallis H-Test Procedure 1. Assign ranks, Ri , to the n combined observations • • Smallest value = 1; largest value = n Average ties 2. Sum ranks for each group 3. Compute test statistic © 2011 Pearson Education, Inc Squared total of each group

Kruskal-Wallis H-Test Example As production manager, you want to see if three filling machines have different filling times. You assign 15 similarly trained and experienced workers, 5 per machine, to the machines. At the. 05 level of significance, is there a difference in the distribution of filling times? Mach 1 Mach 2 Mach 3 25. 40 23. 40 20. 00 26. 31 21. 80 22. 20 24. 10 23. 50 19. 75 23. 74 22. 75 20. 60 25. 10 21. 60 20. 40 © 2011 Pearson Education, Inc

Kruskal-Wallis H-Test Solution • • • H 0: Identical Distrib. Ha: At Least 2 Differ =. 05 df = p – 1 = 3 – 1 = 2 Critical Value(s): =. 05 0 5. 991 c© 2 2011 Pearson Education, Inc

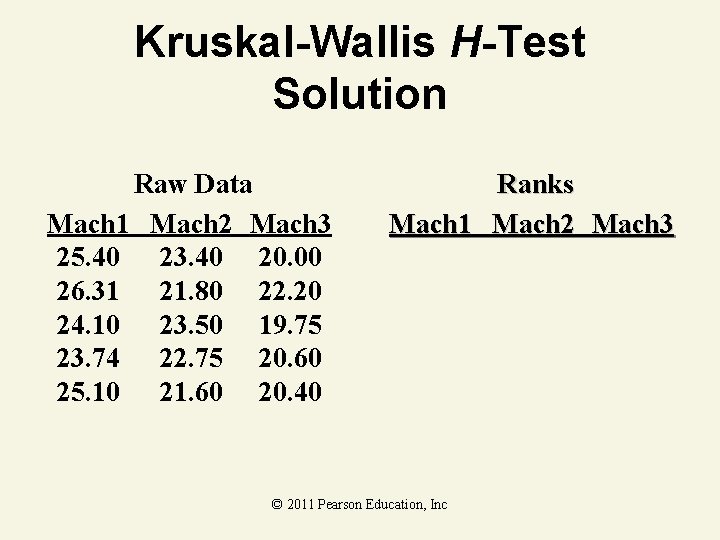
Kruskal-Wallis H-Test Solution Raw Data Mach 1 Mach 2 Mach 3 25. 40 23. 40 20. 00 26. 31 21. 80 22. 20 24. 10 23. 50 19. 75 23. 74 22. 75 20. 60 25. 10 21. 60 20. 40 Ranks Mach 1 Mach 2 Mach 3 © 2011 Pearson Education, Inc

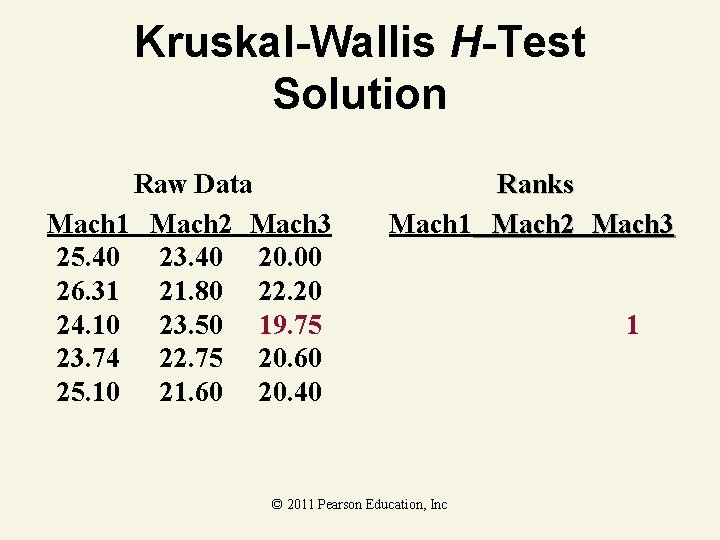
Kruskal-Wallis H-Test Solution Raw Data Mach 1 Mach 2 Mach 3 25. 40 23. 40 20. 00 26. 31 21. 80 22. 20 24. 10 23. 50 19. 75 23. 74 22. 75 20. 60 25. 10 21. 60 20. 40 Ranks Mach 1 Mach 2 Mach 3 © 2011 Pearson Education, Inc 1

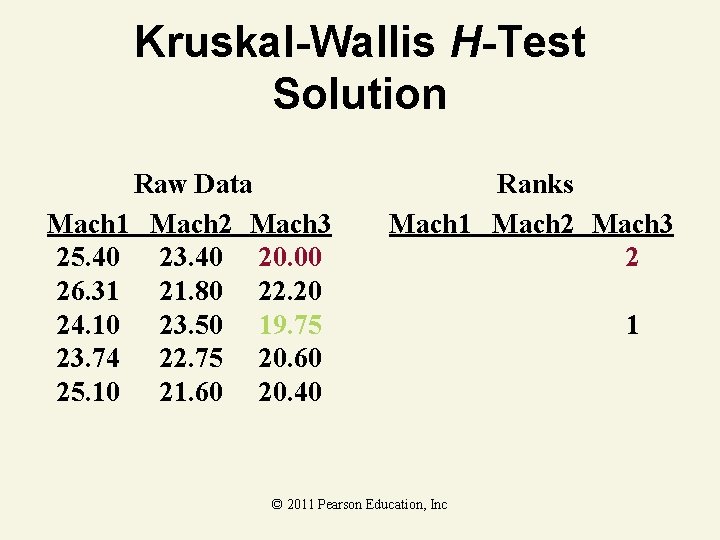
Kruskal-Wallis H-Test Solution Raw Data Mach 1 Mach 2 Mach 3 25. 40 23. 40 20. 00 26. 31 21. 80 22. 20 24. 10 23. 50 19. 75 23. 74 22. 75 20. 60 25. 10 21. 60 20. 40 Ranks Mach 1 Mach 2 Mach 3 2 © 2011 Pearson Education, Inc 1

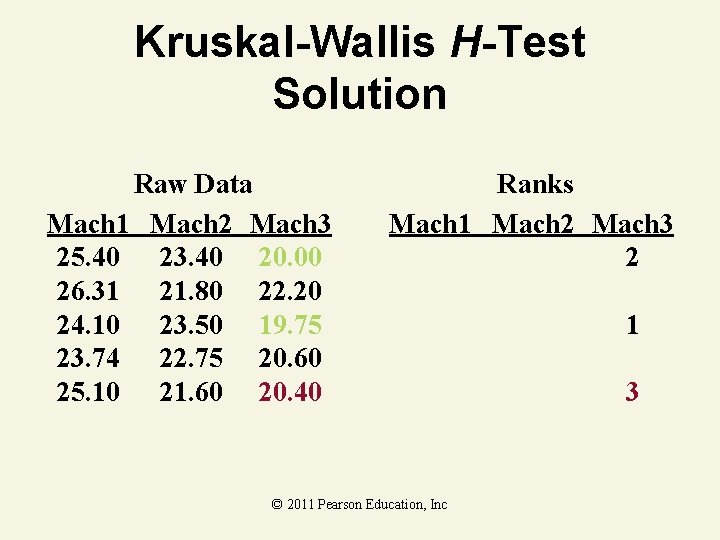
Kruskal-Wallis H-Test Solution Raw Data Mach 1 Mach 2 Mach 3 25. 40 23. 40 20. 00 26. 31 21. 80 22. 20 24. 10 23. 50 19. 75 23. 74 22. 75 20. 60 25. 10 21. 60 20. 40 Ranks Mach 1 Mach 2 Mach 3 2 © 2011 Pearson Education, Inc 1 3

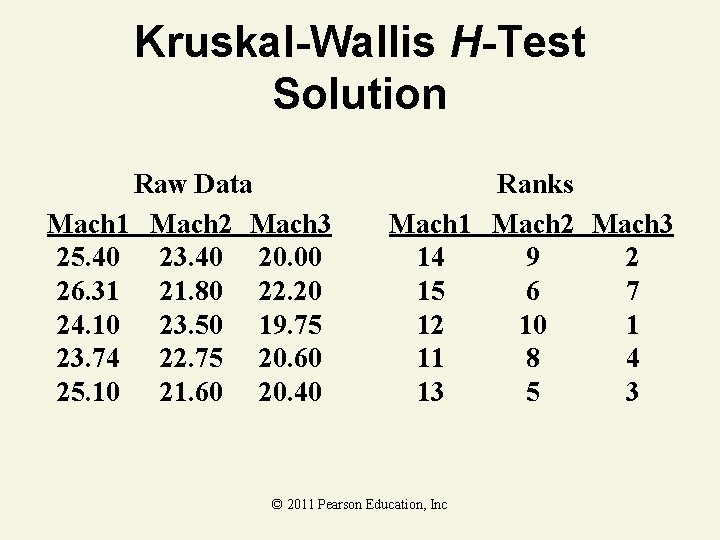
Kruskal-Wallis H-Test Solution Raw Data Mach 1 Mach 2 Mach 3 25. 40 23. 40 20. 00 26. 31 21. 80 22. 20 24. 10 23. 50 19. 75 23. 74 22. 75 20. 60 25. 10 21. 60 20. 40 Ranks Mach 1 Mach 2 Mach 3 14 9 2 15 6 7 12 10 1 11 8 4 13 5 3 © 2011 Pearson Education, Inc

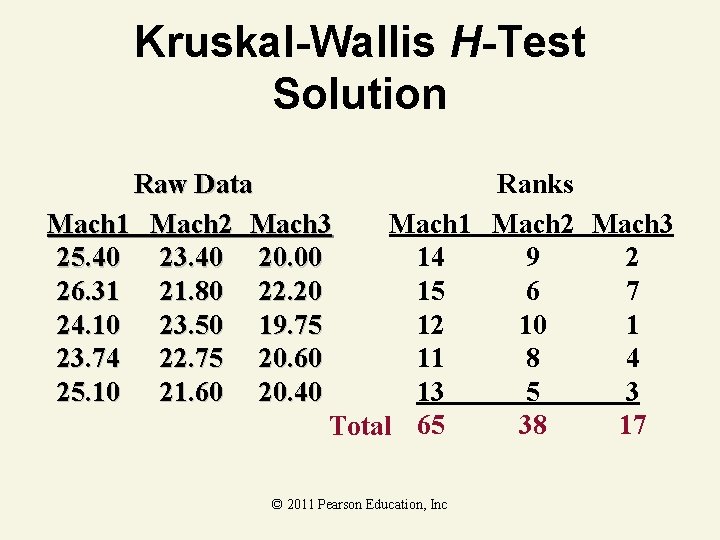
Kruskal-Wallis H-Test Solution Raw Data Ranks Mach 1 Mach 2 Mach 3 25. 40 23. 40 20. 00 14 9 2 26. 31 21. 80 22. 20 15 6 7 24. 10 23. 50 19. 75 12 10 1 23. 74 22. 75 20. 60 11 8 4 25. 10 21. 60 20. 40 13 5 3 38 17 Total 65 © 2011 Pearson Education, Inc

Kruskal-Wallis H-Test Solution © 2011 Pearson Education, Inc

Kruskal-Wallis H-Test Solution • • • H 0: Identical Distrib. Ha: At Least 2 Differ =. 05 df = p – 1 = 3 – 1 = 2 Critical Value(s): =. 05 0 Test Statistic: H = 11. 58 Decision: Reject at =. 05 Conclusion: There is evidence population 5. 991 c© 2 2011 Pearsondistrib. Education, Inc are different

14. 6 Comparing Three or More Populations: Randomized Block Design © 2011 Pearson Education, Inc

Friedman Fr-statistic • provides another method for testing to detect a shift in location of a set of k populations that have the same spread (or, scale) • is based on the rank sums of the treatments, measures the extent to which the k samples differ with respect to their relative ranks within the blocks © 2011 Pearson Education, Inc

Friedman Fr-Test for a Randomized Block Design H 0: The probability distributions for the k treatments are identical Ha: At least two of the probability distributions differ in location Test statistic: © 2011 Pearson Education, Inc

Friedman Fr-Test for a Randomized Block Design where b = Number of blocks k = Number of treatments Rj = Rank sum of the jth treatment, where the rank of each measurement is computed relative to its position within its own block Test statistic: Fr > with (k – 1) degrees of freedom © 2011 Pearson Education, Inc

Friedman Fr-Test for a Randomized Block Design Ties: Assign tied measurements the average of the ranks they would receive if they were unequal but occurred in successive order. For example, if the third-ranked and fourth-ranked measurements are tied, assign each a rank of (3 + 4)/2 = 3. 5. The number should be small relative to the total number of observations. © 2011 Pearson Education, Inc

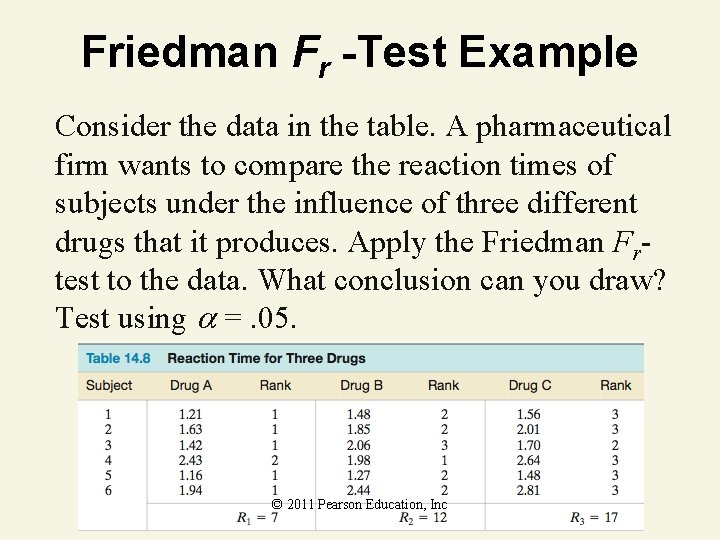
Friedman Fr -Test Example Consider the data in the table. A pharmaceutical firm wants to compare the reaction times of subjects under the influence of three different drugs that it produces. Apply the Friedman Frtest to the data. What conclusion can you draw? Test using =. 05. © 2011 Pearson Education, Inc

Friedman Fr -Test Example H 0: The population distributions of reaction times are identical for the three drugs Ha: At least two of the three drugs have reaction time distributions that differ in location From the table: k = 3 treatments, b = 6 blocks, R 1 = 7, R 2 = 12, R 3 = 17; so © 2011 Pearson Education, Inc

Friedman Fr -Test Example For =. 05, 2. 05 = 5. 99147, therefore Rejection region: H > 5. 99147 © 2011 Pearson Education, Inc

Friedman Fr -Test Example Conclusion: Because H = 8. 33 exceeds the critical value of 5. 99, we reject the null hypothesis and conclude that at least two of the three drugs have distributions of reaction times that differ in location. That is, at least one of the drugs tends to yield reaction times that are faster than the others. © 2011 Pearson Education, Inc

14. 7 Rank Correlation © 2011 Pearson Education, Inc

Spearman’s Rank Correlation Coefficient • Measures correlation between ranks • Corresponds to Pearson product moment correlation coefficient • Values range from – 1 to +1 • Formula (shortcut) di = ui – vi (difference in ranks of ith observation for samples 1 and 2) 2011 Pearson Education, Inc n = number of©pairs of observations

Spearman’s Rank Correlation Procedure 1. Assign ranks, Ri , to the observations of each variable separately 2. Calculate differences, di , between each pair of ranks 3. Square differences, di 2, between ranks 4. Sum squared differences for each variable 5. Use shortcut approximation formula © 2011 Pearson Education, Inc

Spearman’s Rank Correlation Example You’re a research assistant for the FBI. You’re investigating the relationship between a person’s attempts at deception and percent Subj. Deception Pupil changes in their pupil 1 87 10 size. You ask subjects 2 63 6 a series of questions, 3 95 11 some of which they 4 50 7 must answer 5 43 0 dishonestly. At the. 05 level of significance, what is the correlation coefficient? © 2011 Pearson Education, Inc

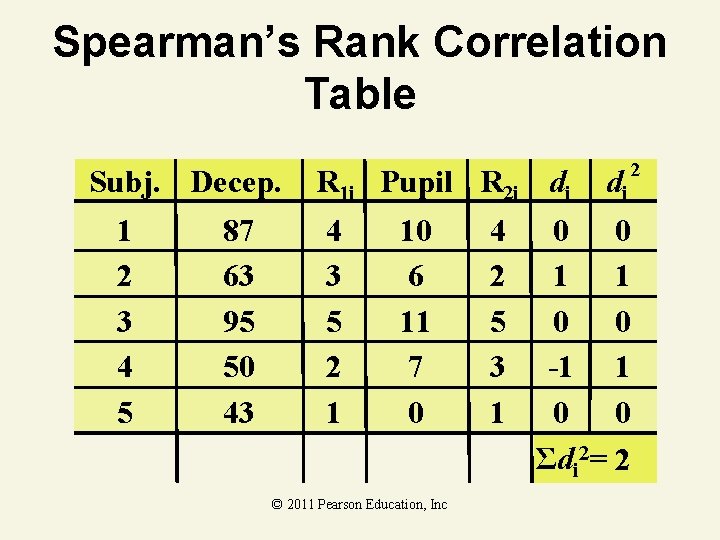
Spearman’s Rank Correlation Table Subj. Decep. 1 2 3 4 5 87 63 95 50 43 R 1 i Pupil R 2 i di 4 3 5 2 1 10 6 11 7 0 © 2011 Pearson Education, Inc 4 2 5 3 1 di 2 0 0 1 1 0 0 -1 1 0 0 Σdi 2= 2

Spearman’s Rank Correlation Solution © 2011 Pearson Education, Inc

Spearman’s Nonparametric Test for Rank Correlation One-Tailed Test H 0: = 0 Ha: > 0 (or Ha: < 0) Test statistic: Rejection region: rs > rs, or rs <–rs, when s < 0 where rs, is the value from Table XVI corresponding to the upper-tail area and n pairs of observations © 2011 Pearson Education, Inc

Spearman’s Nonparametric Test for Rank Correlation Ties: Assign tied measurements the average of the ranks they would receive if they were unequal but occurred in successive order. For example, if the third-ranked and fourth-ranked measurements are tied, assign each a rank of (3 + 4)/2 = 3. 5. The number should be small relative to the total number of observations. © 2011 Pearson Education, Inc

Spearman’s Nonparametric Test for Rank Correlation Two-Tailed Test H 0: = 0 Ha : ≠ 0 Test statistic: Rejection region: |rs | > rs, where rs, is the value from Table XVI corresponding to the upper-tail area and n pairs of observations © 2011 Pearson Education, Inc

Spearman’s Nonparametric Test for Rank Correlation Ties: Assign tied measurements the average of the ranks they would receive if they were unequal but occurred in successive order. For example, if the third-ranked and fourth-ranked measurements are tied, assign each a rank of (3 + 4)/2 = 3. 5. The number should be small relative to the total number of observations. © 2011 Pearson Education, Inc

Conditions Required for a Valid Spearman’s Test 1. The sample of experimental units on which the two variables are measured is randomly selected. 2. The probability distributions of the two variables are continuous. © 2011 Pearson Education, Inc

Key Ideas Distribution-Free Tests Do not rely on assumptions about the probability distribution of the sampled population © 2011 Pearson Education, Inc

Key Ideas Nonparametrics Distribution-free tests that are based on rank statistics One-sample nonparametric test for the population median – sign test Nonparametric test for two independent samples – Wilcoxon rank sum test Nonparametric test for matched pairs – Wilcoxon signed rank test © 2011 Pearson Education, Inc

Key Ideas Nonparametric test for a completely randomized design – Kruskal-Wallis test Nonparametric test for a randomized block design – Friedman test Nonparametric test for rank correlation – Spearman’s test © 2011 Pearson Education, Inc