Chapter 4 Applications of Derivatives 1 4 1




































































- Slides: 97

Chapter 4 Applications of Derivatives 1

4. 1 Extreme Values of Functions 2

3

4

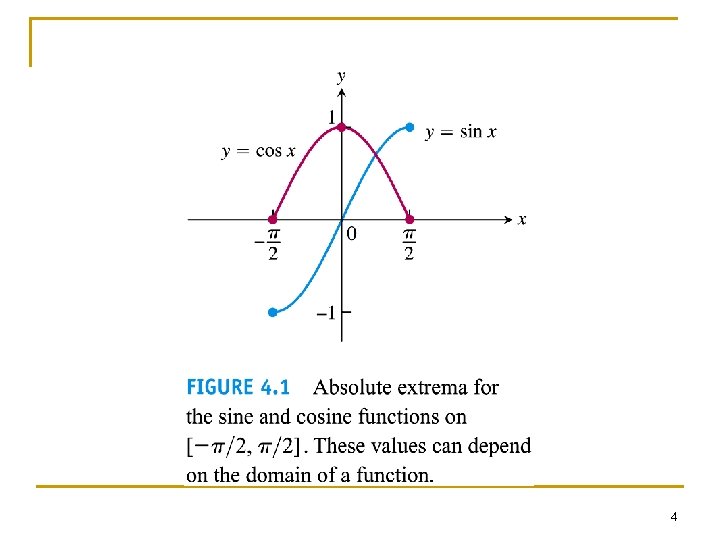
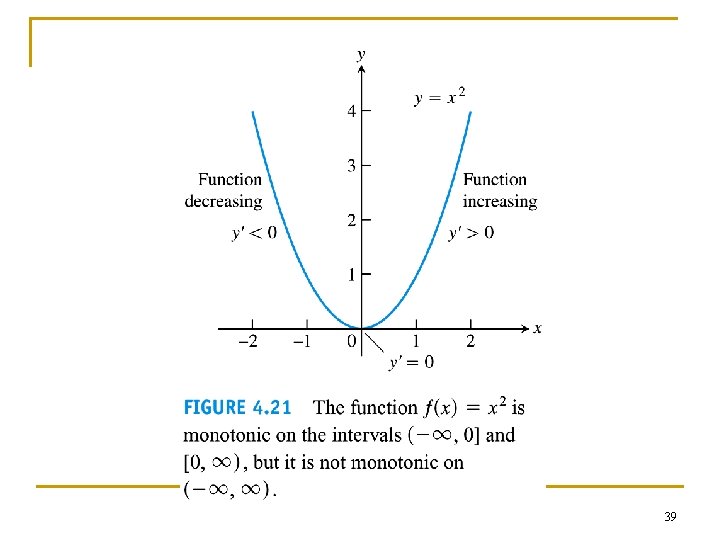
Example 1 n n Exploring absolute extrema The absolute extrema of the following functions on their domains can be seen in Figure 4. 2 5

6

7

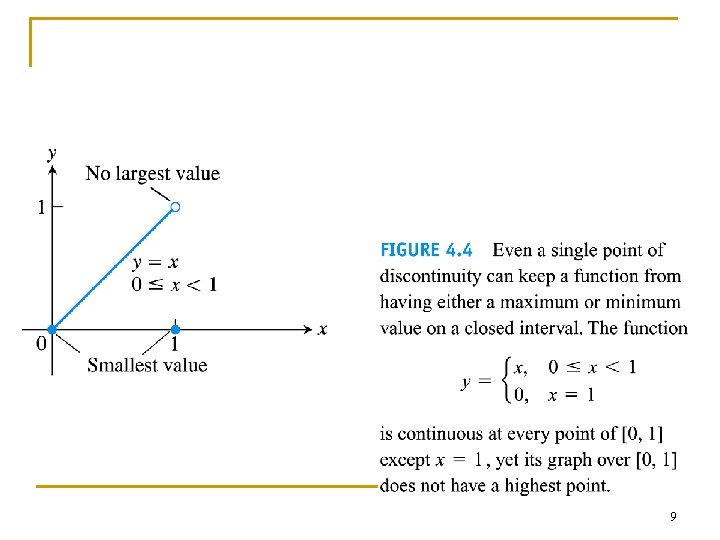
8

9

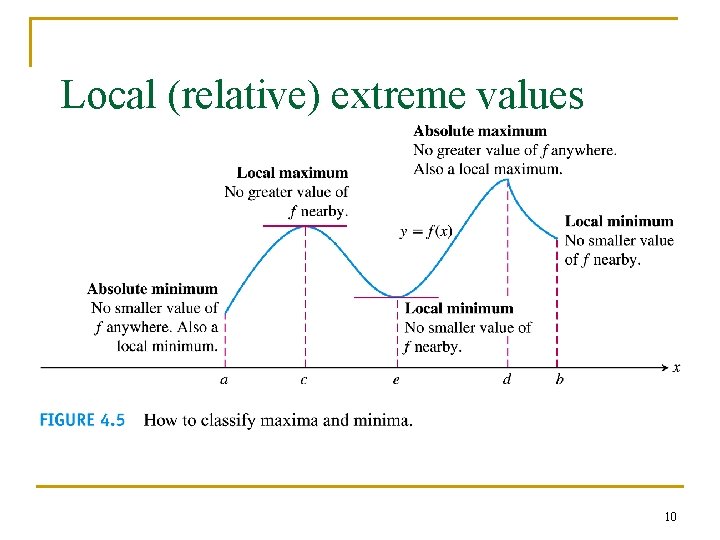
Local (relative) extreme values 10

11

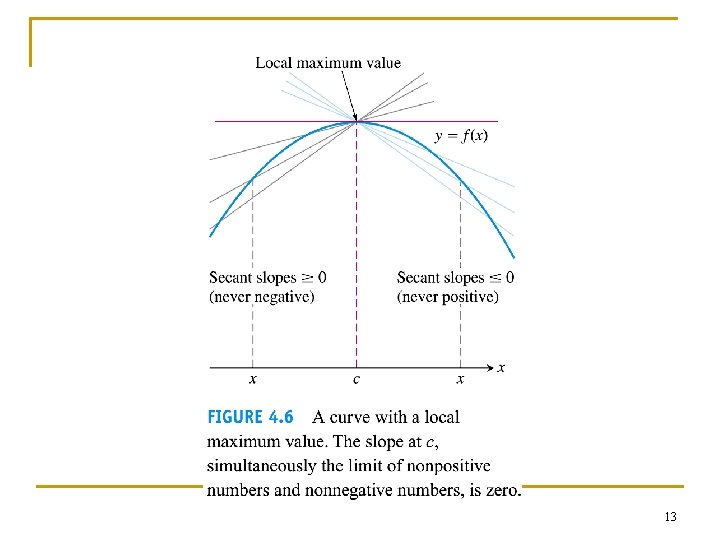
Finding Extrema…with a notalways-effective method. 12

13

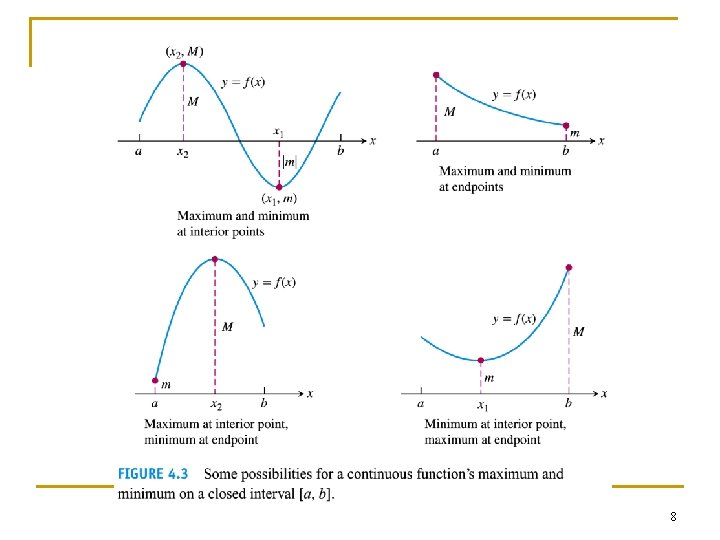
How to find the absolute extrema of a continuous function f on a finite closed interval 1. Evaluate f at all critical point and endpoints 2. Take the largest and smallest of these values. 14

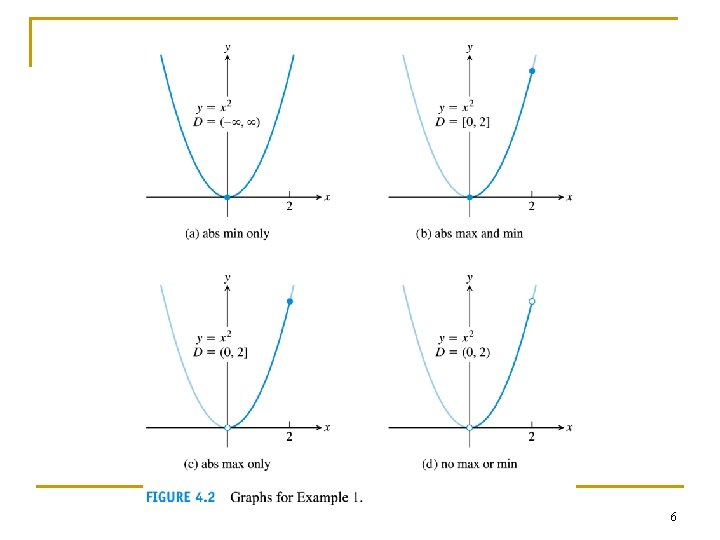
Example 2: Finding absolute extrema n Find the absolute maximum and minimum of f(x) = x 2 on [-2, 1]. 15

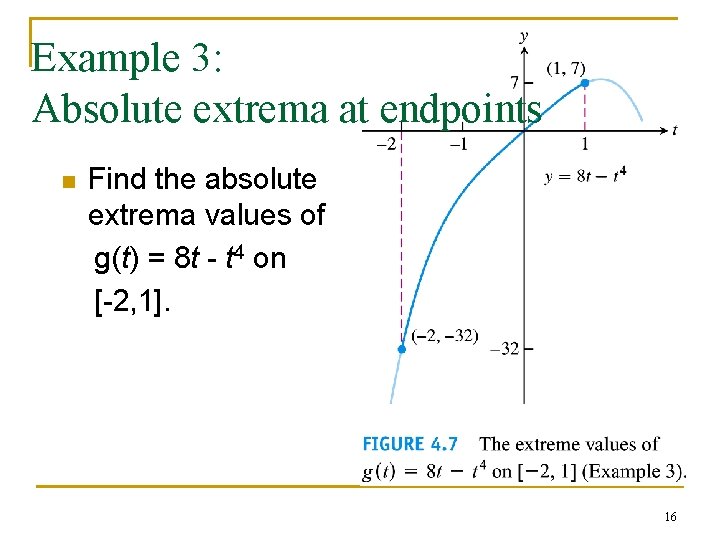
Example 3: Absolute extrema at endpoints n Find the absolute extrema values of g(t) = 8 t - t 4 on [-2, 1]. 16

Example 4: Finding absolute extrema on a closed interval n Find the absolute maximum and minimum values of f (x) = x 2/3 on the interval [-2, 3]. 17

18

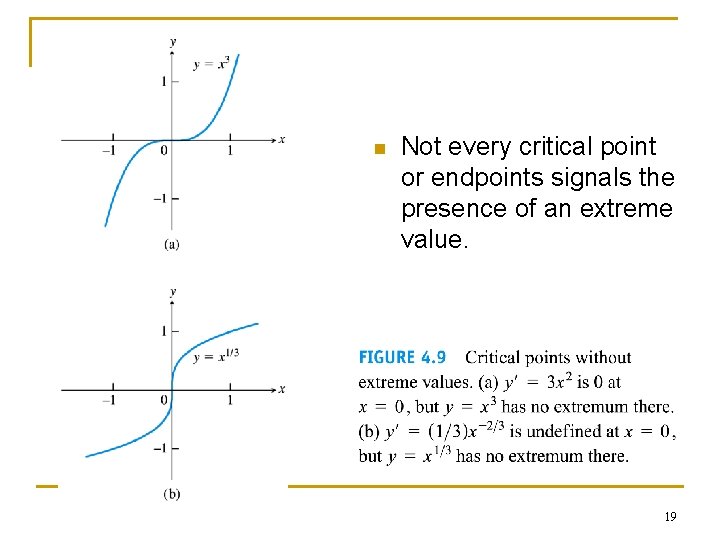
n Not every critical point or endpoints signals the presence of an extreme value. 19

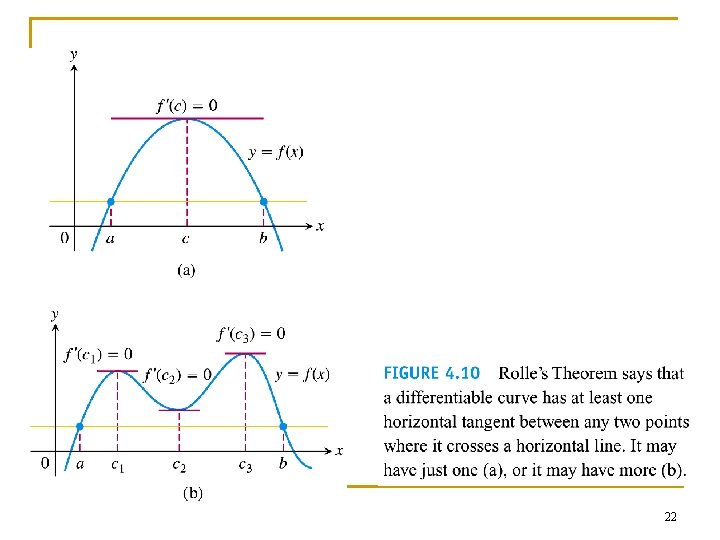
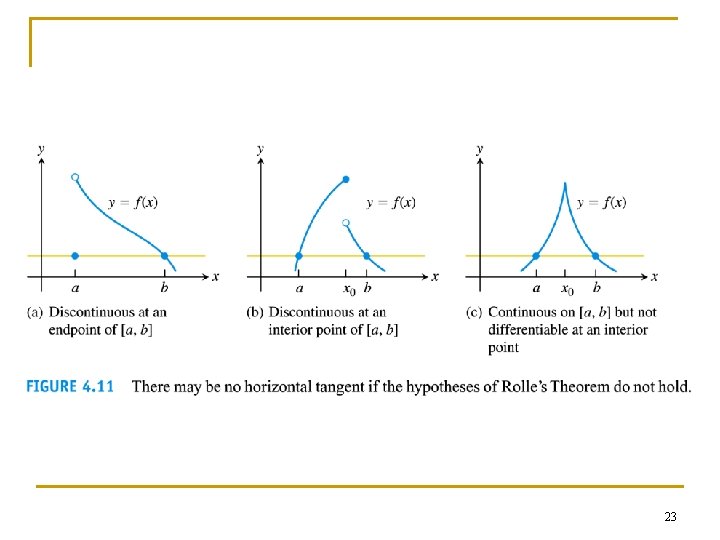
4. 2 The Mean Value Theorem 20

21

22

23

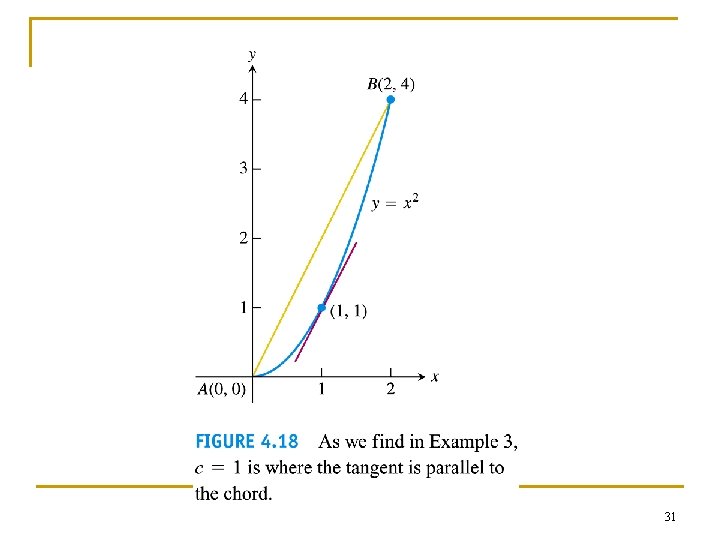
Example 1 n Horizontal tangents of a cubit polynomial 24

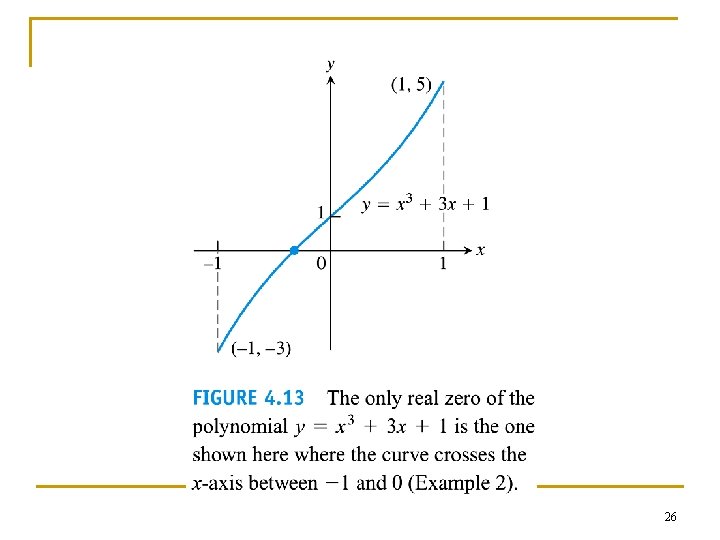
Example 2 Solution of an equation f(x)=0 n Show that the equation has exactly one real solution. Solution 1. Apply Intermediate value theorem to show that there exist at least one root 2. Apply Rolle’s theotem to prove the uniqueness of the root. 25

26

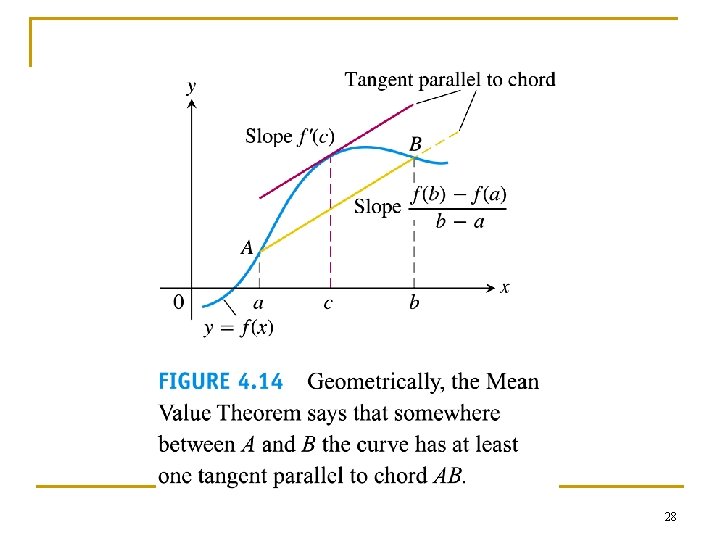
The mean value theorem 27

28

29

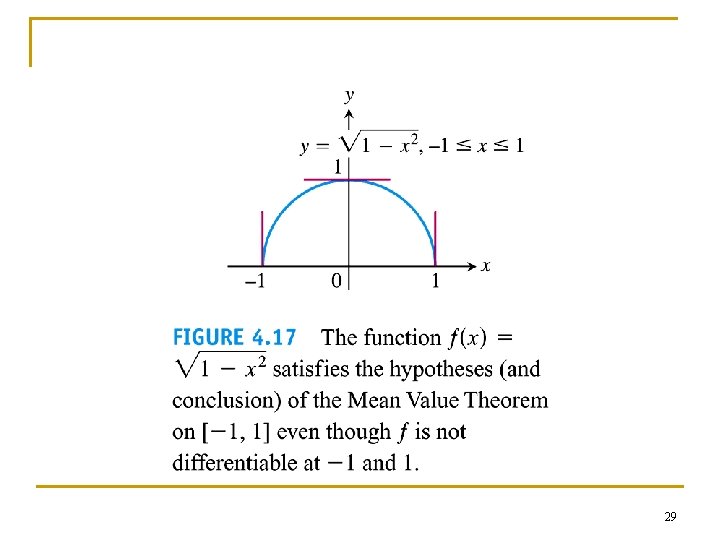
Example 3 n The function is continuous for 0 ≤ x≤ 2 and differentiable for 0 < x < 2. 30

31

Mathematical consequences 32

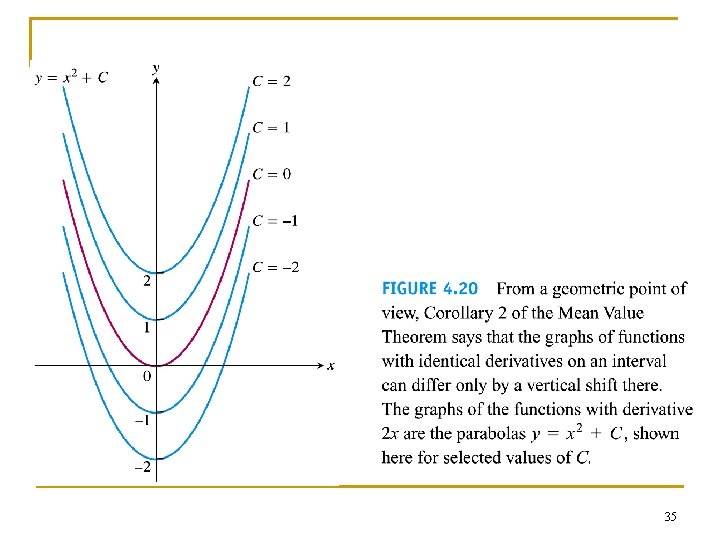
Corollary 1 can be proven using the Mean Value Theorem n n Say x 1, x 2 (a, b) such that x 1 < x 2 By the MVT on [x 1, x 2] there exist some point c between x 1 and x 2 such that f '(c)= (f (x 2) –f (x 1))/(x 2 - x 1) Since f '(c) = 0 throughout (a, b), f (x 2) – f (x 1) = 0, hence f (x 2) = f (x 1) for x 1, x 2 (a, b). This is equivalent to f(x) = a constant for x (a, b). 33

Proof of Corollary 2 n n At each point x (a, b) the derivative of the difference between function h=f – g is h'(x) = f '(x) –g'(x) = 0 Thus h(x) = C on (a, b) by Corollary 1. That is f (x) –g(x) = C on (a, b), so f (x) = C + g(x). 34

35

Example 5 n Find the function f(x) whose derivative is sin x and whose graph passes through the point (0, 2). 36

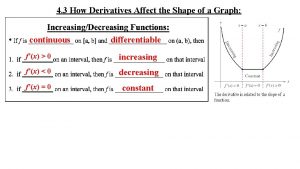
4. 3 Monotonic Functions and The First Derivative Test 37

Increasing functions and decreasing functions 38

39

Mean value theorem is used to prove Corollary 3 40

Example 1 Using the first derivative test for monotonic functions n Find the critical point of and identify the intervals on which f is increasing and decreasing. Solution n 41

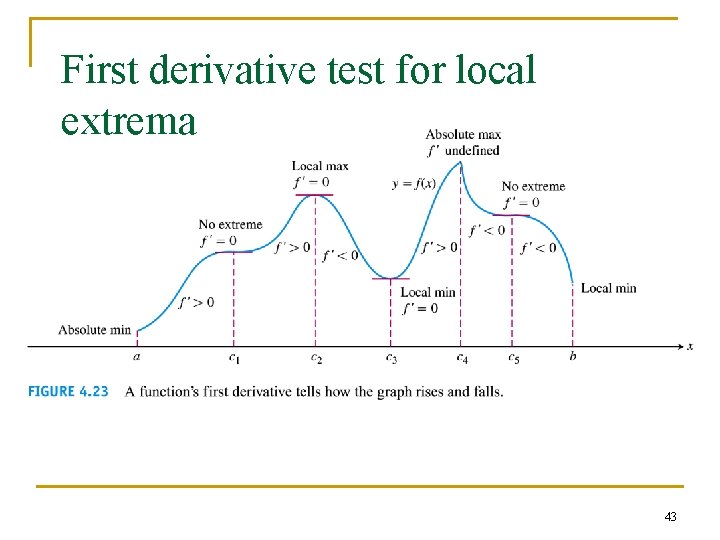
42

First derivative test for local extrema 43

44

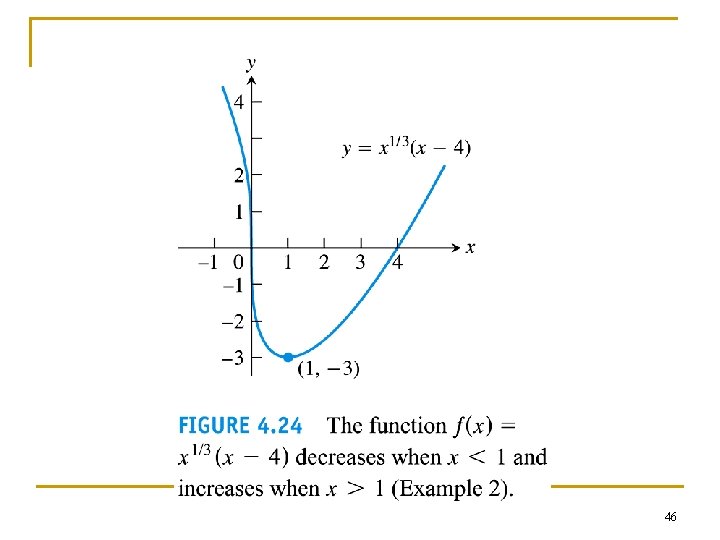
Example 2: Using the first derivative test for local extrema n Find the critical point of n Identify the intervals on which f is increasing and decreasing. Find the function’s local and absolute extreme values. 45

46

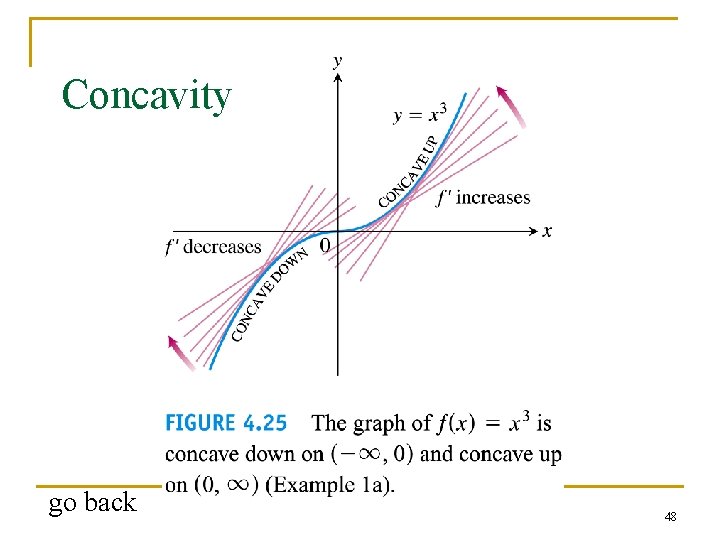
4. 4 Concavity and Curve Sketching 47

Concavity go back 48

49

50

Example 1(a): Applying the concavity test n n n Check the concavity of the curve y = x 3 Solution: y'' = 6 x y'' < 0 for x < 0; y'' > 0 for x > 0; Link to Figure 4. 25 51

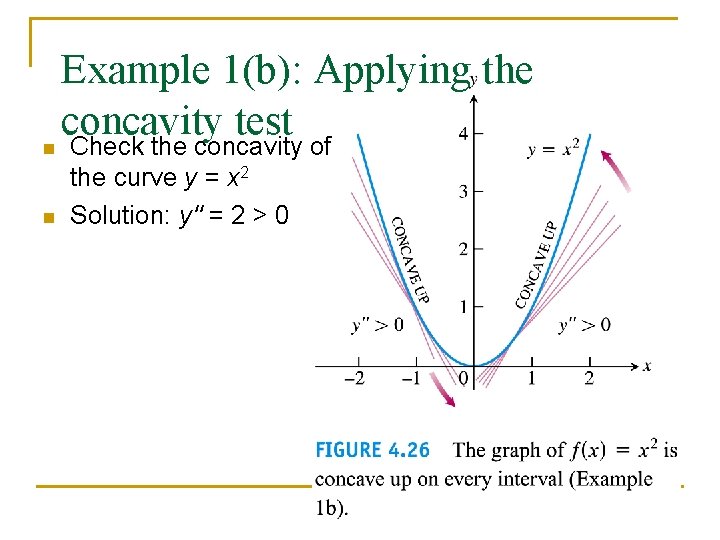
n n Example 1(b): Applying the concavity test Check the concavity of the curve y = x 2 Solution: y'' = 2 > 0 52

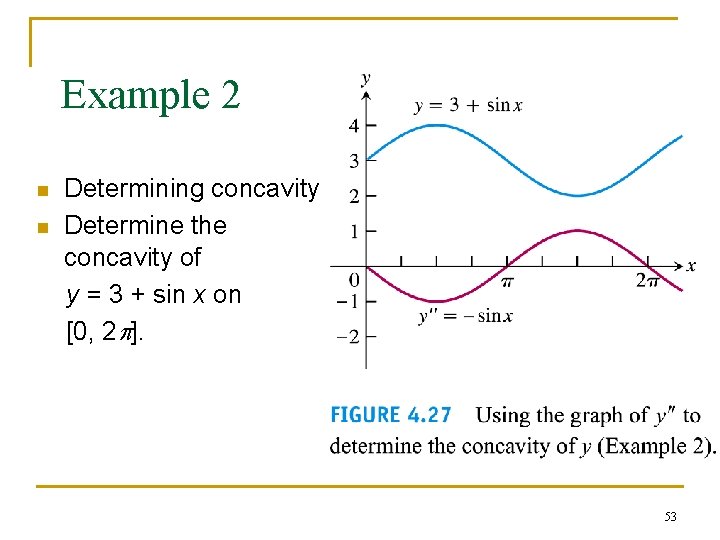
Example 2 n n Determining concavity Determine the concavity of y = 3 + sin x on [0, 2 p]. 53

Point of inflection 54

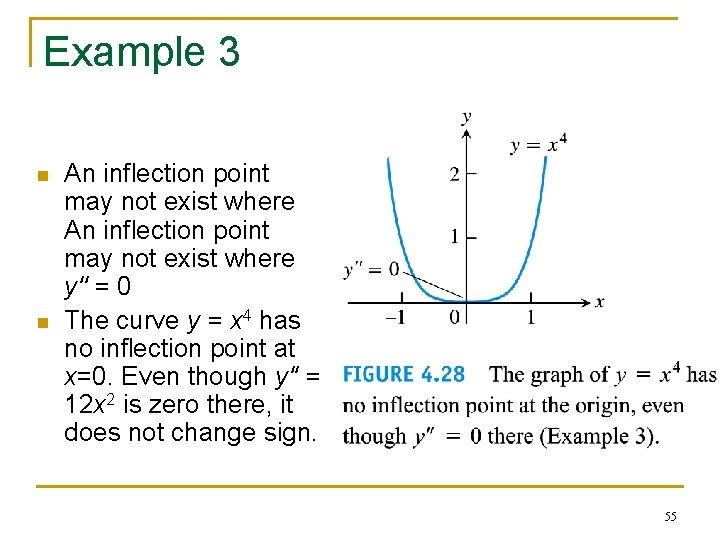
Example 3 n n An inflection point may not exist where y'' = 0 The curve y = x 4 has no inflection point at x=0. Even though y'' = 12 x 2 is zero there, it does not change sign. 55

Example 4 n n n An inflection point may occur where y'' = 0 does not exist The curve y = x 1/3 has a point of inflection at x=0 but y'' does not exist there. y'' = -(2/9)x-5/3 56

Second derivative test for local extrema 57

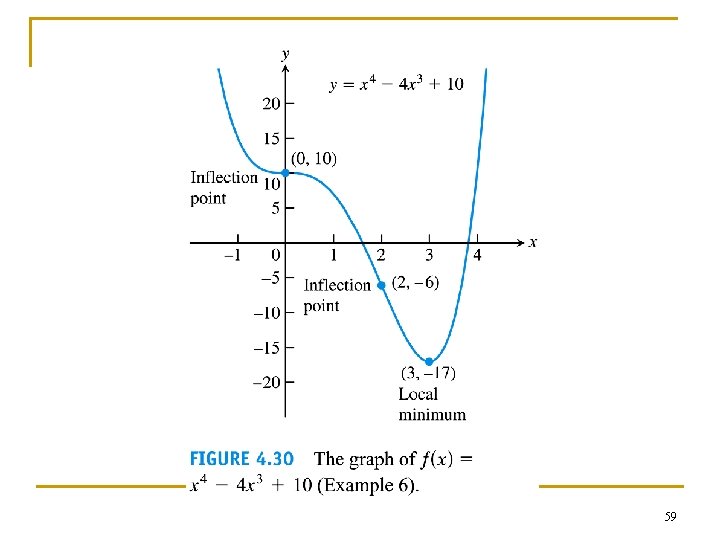
Example 6: Using f ' and f '' to graph f n (a) (b) (c) (d) (e) (f) Sketch a graph of the function f (x) = x 4 - 4 x 3 + 10 using the following steps. Identify where the extrema of f occur Find the intervals on which f is increasing and the intervals on which f is decreasing Find where the graph of f is concave up and where it is concave down. Identify the slanted/vertical/horizontal asymtots, if there is any Sketch the general shape of the graph for f. Plot the specific points. Then sketch the graph. 58

59

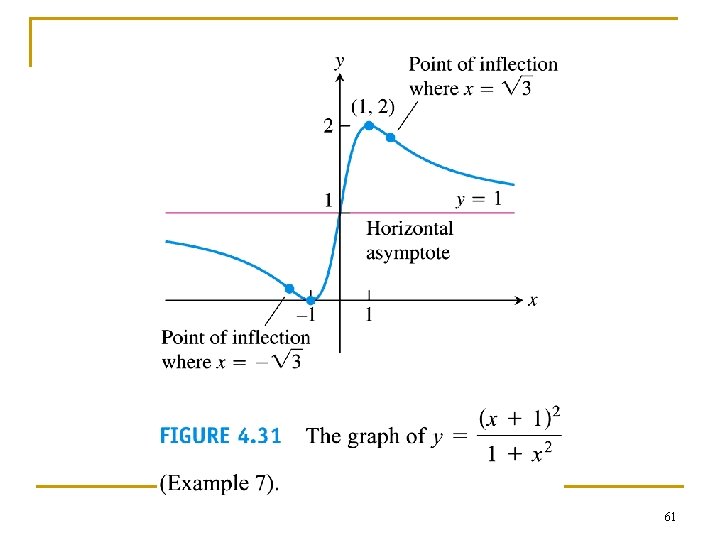
Example n n n Using the graphing strategy Sketch the graph of f (x) = (x + 1)2 / (x 2 + 1). 60

61

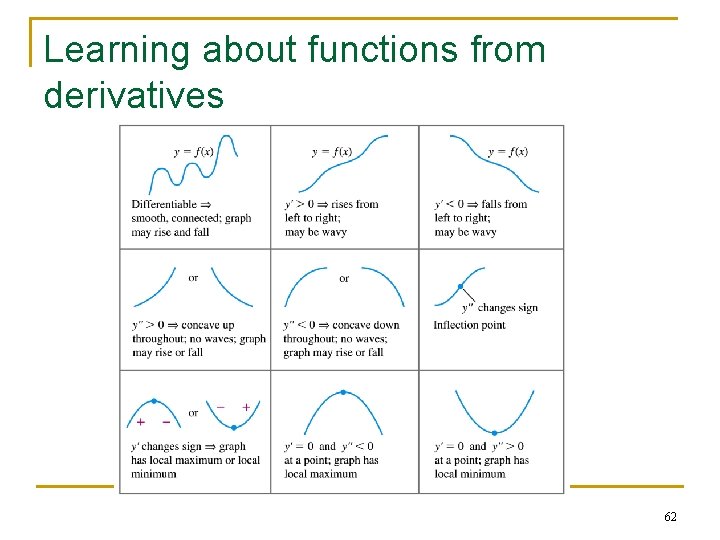
Learning about functions from derivatives 62

4. 5 Applied Optimization Problems 63

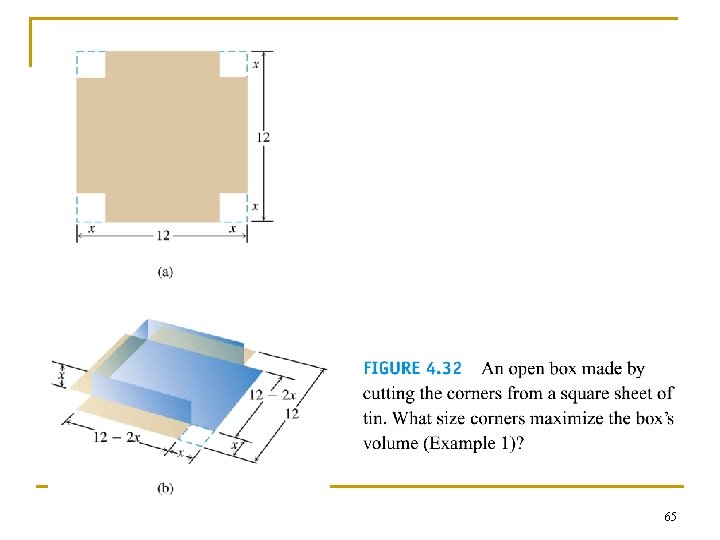
Example 1 n An open-top box is to be cutting small congruent squares from the corners of a 12 -in. -by-12 -in. sheet of tin and bending up the sides. How large should the squares cut from the corners be to make the box hold as much as possible? 64

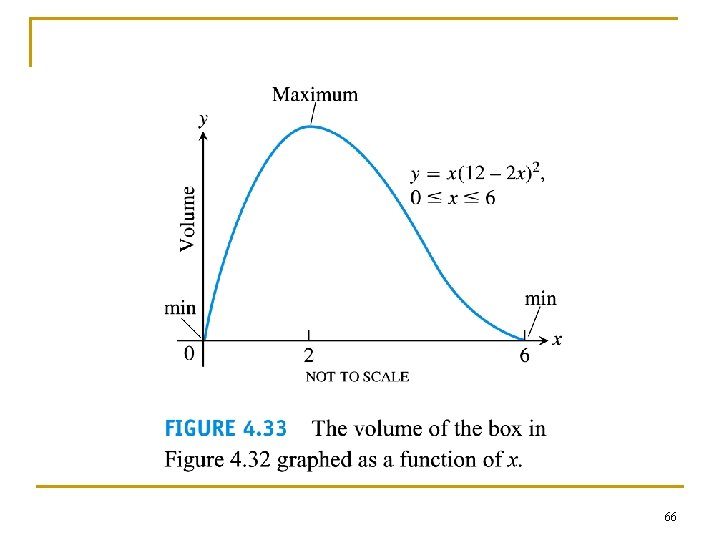
65

66

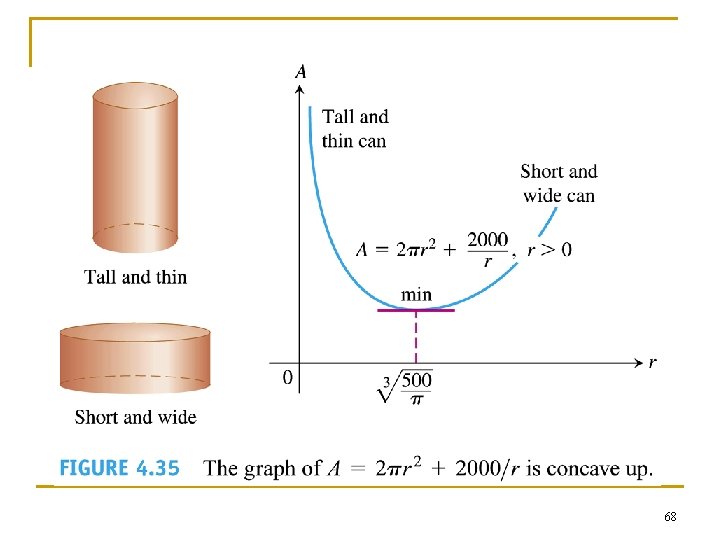
Example 2 n n Designing an efficient cylindrical can Design a 1 -liter can shaped like a right circular cylinder. What dimensions will use the least material? 67

68

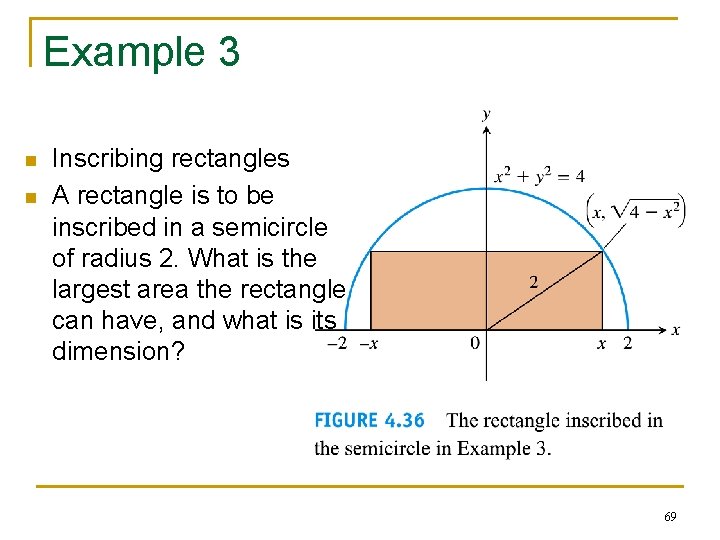
Example 3 n n Inscribing rectangles A rectangle is to be inscribed in a semicircle of radius 2. What is the largest area the rectangle can have, and what is its dimension? 69

Solution n n Form the function of the area A as a function of x: A=A(x)=x(4 -x 2)1/2; x > 0. Seek the maximum of A: 70

4. 6 Indeterminate Forms and L’ Hopital’s Rule 71

Indeterminate forms 0/0 72

Example 1 n Using L’ Hopital’s Rule (a) n (b) n 73

74

Example 2(a) n n Applying the stronger form of L’ Hopital’s rule (a) 75

Example 2(b) n n Applying the stronger form of L’ Hopital’s rule (b) 76

77

78

Example 3 n Incorrect application of the stronger form of L’ Hopital’s 79

Example 4 n Using l’ Hopital’s rule with one-sided limits 80

Indeterminate forms ∞/∞, ∞ 0, ∞∞ n If f ∞ and g ∞ as x a, then n a may be finite or infinite 81

Example 5 Working with the indeterminate form ∞/∞ 82

Example 5(b) 83

Example 6 n Working with the indeterminate form ∞ 0 84

Example 7 n Working with the indeterminate form ∞ - ∞ 85

4. 8 Antiderivatives 86

Finding antiderivatives 87

Example 1 n n n Finding antiderivatives Find an antiderivative for each of the following functions (a) f(x) = 2 x (b) f(x) = cos x (c) h(x) = 2 x + cos x 88

The most general antiderivative 89

Example 2 Finding a particular antiderivative n n n Find an antiderivative of f (x) = sin x that satisfies F(0) = 3 Solution: F(x)=cos x + C is the most general form of the antiderivative of f(x). We require F(x) to fulfill the condition that when x=3 (in unit of radian), F(x)=0. This will fix the value of C, as per F(3)= 3 = cos 3 + C 3 - cos 3 Hence, F(x)= cos x + (3 - cos 3) is the antiderivative sought 90

91

Example 3 Finding antiderivatives using table 4. 2 n n n Find the general antiderivative of each of the following functions. (a) f (x) = x 5 (b) g (x) = 1/x 1/2 (c) h (x) = sin 2 x (d) i (x) = cos (x/2) 92

Example 4 Using the linearity rules for antiderivatives n n Find the general antiderivative of f (x) = 3/x 1/2 + sin 2 x 93

n In other words, given a function f(x), the most general form of its antiderivative, previously represented by the symbol F(x) + C, where C denotes an arbitrary constant, is now being represented in the form of an indefinite integral, namely, 94

Operationally, the indefinite integral of f(x) means Operationally, the indefinite integral of f(x) is the inverse of the operation of derivative taking of f(x) Antiderivative of f(x) Derivative of F(x) 95

Example of indefinite integral notation 96

Example 7 Indefinite integration done term-by term and rewriting the constant of integration n Evaluate 97
 Chapter 4 applications of derivatives
Chapter 4 applications of derivatives Chapter 4 applications of derivatives
Chapter 4 applications of derivatives Computer skills for preparatory programs
Computer skills for preparatory programs Vehicle maneuvers
Vehicle maneuvers Principles of economics chapter 28 answers
Principles of economics chapter 28 answers Chapter 23:1 performing range of motion exercises
Chapter 23:1 performing range of motion exercises Chapter 8 linear programming applications solutions
Chapter 8 linear programming applications solutions The life skill practicing wellness is
The life skill practicing wellness is Line regulation
Line regulation Lingual pouch definition
Lingual pouch definition Algebraic differentiation
Algebraic differentiation Implicit derivative
Implicit derivative Brown sauce derivatives
Brown sauce derivatives Find y
Find y Cleft and pouch
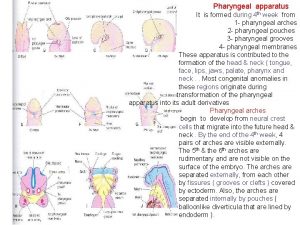
Cleft and pouch Pharyngeal pouches derivatives
Pharyngeal pouches derivatives Least reactive carboxylic acid derivatives
Least reactive carboxylic acid derivatives Mesoderm derivatives
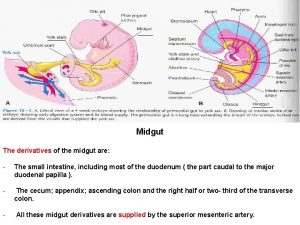
Mesoderm derivatives Derivatives of midgut
Derivatives of midgut Differentiation
Differentiation Hydroxy derivatives
Hydroxy derivatives Samina anjum
Samina anjum Higher order derivatives real life examples
Higher order derivatives real life examples Hedging in forward market
Hedging in forward market Mesoderma paraxial
Mesoderma paraxial Derivative of the exponential function
Derivative of the exponential function Development of superior vena cava
Development of superior vena cava Vitelline vein derivatives
Vitelline vein derivatives Derivatives week
Derivatives week Stoxx blue chip
Stoxx blue chip Derivative of constant number
Derivative of constant number Regular warp rib weave
Regular warp rib weave Derivatives of inverse functions and logarithms
Derivatives of inverse functions and logarithms Sec derivative
Sec derivative Derivatives 2
Derivatives 2 Derivative formula
Derivative formula Derivatives asset class
Derivatives asset class Hyperbolic functions derivatives
Hyperbolic functions derivatives Finite divided difference
Finite divided difference Carboxylic acid derivatives
Carboxylic acid derivatives Forwards vs futures vs options vs swaps
Forwards vs futures vs options vs swaps Carboxylic acids and their derivatives
Carboxylic acids and their derivatives Carboxylic acid formula
Carboxylic acid formula Reactivity of carboxylic acid derivatives
Reactivity of carboxylic acid derivatives Fischer esterification
Fischer esterification 4th aortic arch derivatives
4th aortic arch derivatives Trilaminar disc derivatives
Trilaminar disc derivatives Metencephalon derivatives
Metencephalon derivatives General derivative formula
General derivative formula Second partial derivative formula
Second partial derivative formula Thickening agents for sauce
Thickening agents for sauce Financial engineering derivatives and risk management
Financial engineering derivatives and risk management Contoh soal determinan jacobian
Contoh soal determinan jacobian Turunan parsial tingkat tinggi
Turunan parsial tingkat tinggi Carboxylic acid metabolism
Carboxylic acid metabolism Radian area
Radian area Derivatives graphing calculator
Derivatives graphing calculator Since
Since Derivatives of position
Derivatives of position Somite derivatives
Somite derivatives Limits and derivatives class 11 pdf
Limits and derivatives class 11 pdf Wesentlichkeitstheorie
Wesentlichkeitstheorie How derivatives affect the shape of a graph
How derivatives affect the shape of a graph Derivatives of position
Derivatives of position Blt method will convert analog filter to dt filter that has
Blt method will convert analog filter to dt filter that has Rules of differentiation
Rules of differentiation Differentiation數學
Differentiation數學 Differential calculus formulas
Differential calculus formulas Chain rule partial derivatives second order
Chain rule partial derivatives second order How derivatives affect the shape of a graph
How derivatives affect the shape of a graph Derivatives formulas
Derivatives formulas Limits and derivatives
Limits and derivatives Vitamin k deficiency
Vitamin k deficiency Product and quotient rules and higher order derivatives
Product and quotient rules and higher order derivatives Benzene derivatives
Benzene derivatives Characteristics of derivatives
Characteristics of derivatives Derivatives and the shape of a graph
Derivatives and the shape of a graph Derivatives of grid computing
Derivatives of grid computing Declared dividend index futures
Declared dividend index futures Transforms of derivatives
Transforms of derivatives Non financial derivatives
Non financial derivatives Derivatives time bomb
Derivatives time bomb Options, futures, and other derivatives
Options, futures, and other derivatives Example of derivatives
Example of derivatives Acyl derivatives
Acyl derivatives Puella derivatives
Puella derivatives Bio380 utm
Bio380 utm Functional derivatives of carboxylic acids
Functional derivatives of carboxylic acids Euronext commodities derivatives
Euronext commodities derivatives Cme weather
Cme weather Acylation of benzene
Acylation of benzene St x
St x Total return swap
Total return swap Limits and derivatives
Limits and derivatives Tree diagram partial derivatives
Tree diagram partial derivatives Describe sauce
Describe sauce Differentiate composite functions
Differentiate composite functions 3rd and 4th pharyngeal pouches
3rd and 4th pharyngeal pouches