Second Order Partial Derivatives Since derivatives of functions

Second Order Partial Derivatives Since derivatives of functions are themselves functions, they can be differentiated. Remember for 1 independent variable, we differentiated f'(x) to get f"(x), the 2 nd derivative. We have a similar situation for functions of 2 independent variables.

Second Order Partial Derivatives We have a similar situation for functions of 2 independent variables. You have seen that the partial derivatives of functions are also functions. So we differentiate them. However, since the 1 st partial derivative can be a function of both independent variables, we have more possible 2 nd derivatives.

Second Order Partial Derivatives If z = f(x, y), then we find: How many ways can we differentiate fx? ?

Second Order Partial Derivatives If z = f(x, y), then we find: How many ways can we differentiate fx? ? Since fx is a function of x and y, we may find partial derivatives with respect to both x and y!

Second Order Partial Derivatives If z = f(x, y), then we find: Since fx is a function of x and y, we may find partial derivatives with respect to both x and y!

Second Order Partial Derivatives If z = f(x, y), then we find: Since fy is a function of x and y, we may find partial derivatives with respect to both x and y!

Second Order Partial Derivatives Remember 2 nd derivatives from Calculus 1? What did they tell us about a function of 1 independent variable? ?

Second Order Partial Derivatives The 2 nd derivative tells us about the curvature of the f(x). If f"(x)>0 near a point, what do we know? ? If f"(x)>0 in an interval around x, the function is concave up on that interval. If f"(x)<0 in an interval around x, the function is concave down on that interval.

Second Order Partial Derivatives If f"(x)>0 in an interval around x, the function is concave up on that interval. If f"(x)<0 in an interval around x, the function is concave down on that interval. Can you carry these ideas over for fxx and fyy?

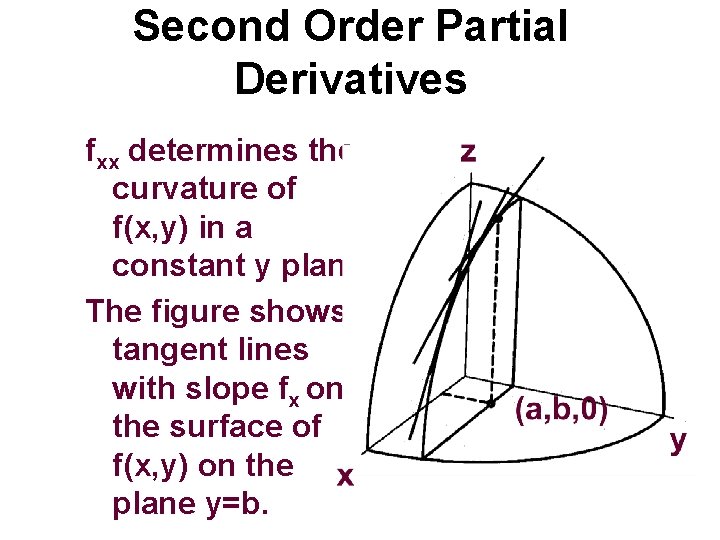
Second Order Partial Derivatives fxx determines the curvature of f(x, y) in a constant y plane. The figure shows tangent lines with slope fx on the surface of f(x, y) on the plane y=b.

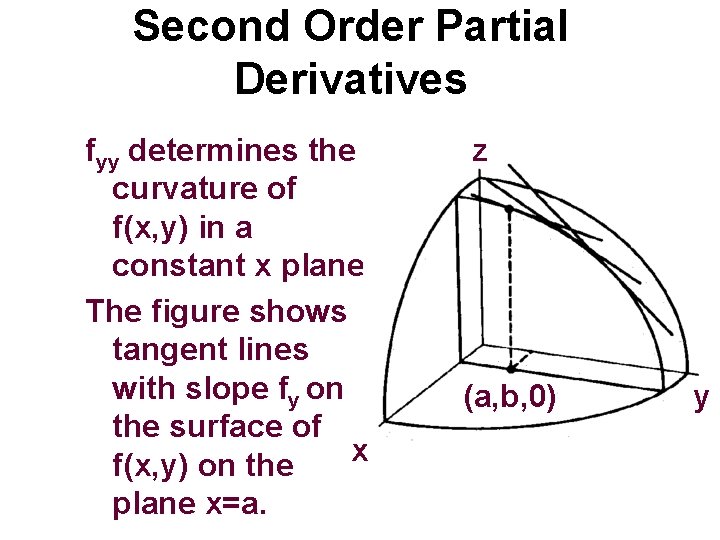
Second Order Partial Derivatives fyy determines the curvature of f(x, y) in a constant x plane. The figure shows tangent lines with slope fy on the surface of x f(x, y) on the plane x=a. z (a, b, 0) y

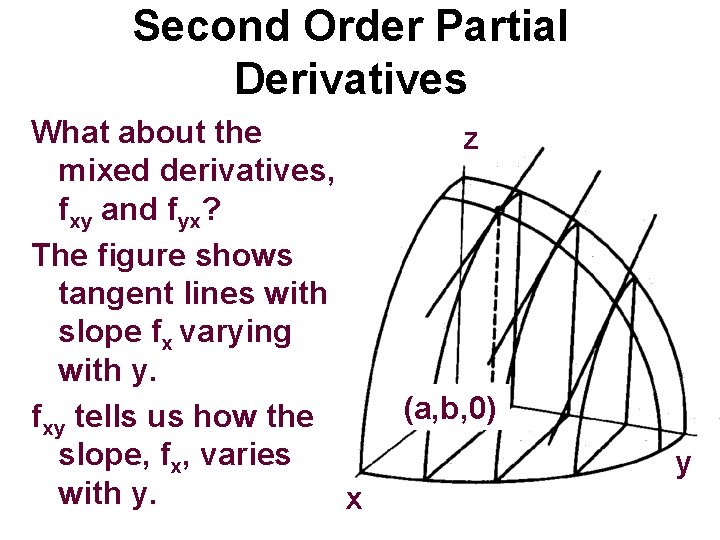
Second Order Partial Derivatives What about the mixed derivatives, fxy and fyx? The figure shows tangent lines with slope fx varying with y. fxy tells us how the slope, fx, varies with y. x z (a, b, 0) y

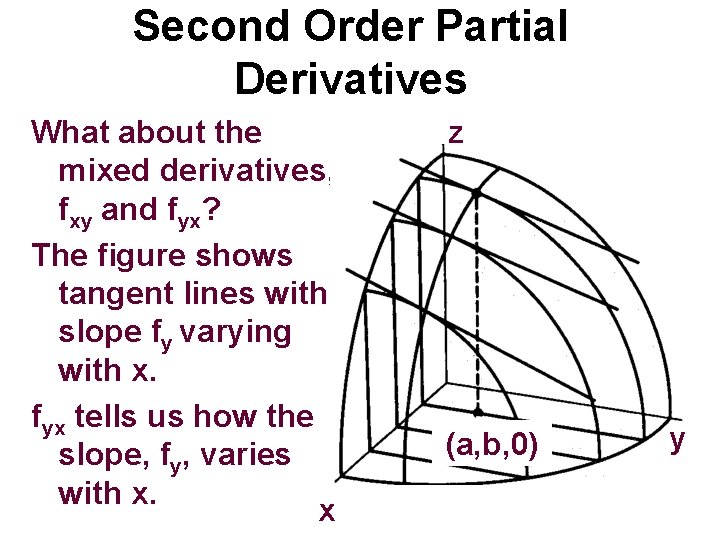
Second Order Partial Derivatives What about the mixed derivatives, fxy and fyx? The figure shows tangent lines with slope fy varying with x. fyx tells us how the slope, fy, varies with x. x z (a, b, 0) y

Second Order Partial Derivatives Examples: Find all 2 nd partial derivatives: a) b) c)

Local Extrema Remember again from Calculus 1 and 2 for functions of 1 independent variable how you found local extrema. What is the difference between global and local extrema? What were the tests you can use to determine local extrema?

Local Extrema Recall: f has a local maximum at the point Po, if f(Po) f(P) for all point P near Po. f has a local minimum at the point Po, if f(Po) f(P) for all point P near Po. What do we mean by critical points of a function of 1 variable, f(x)? How do we find critical points for f(x)?

Local Extrema Recall: f has a local maximum at the point Po, if f(Po) f(P) for all point P near Po. f has a local minimum at the point Po, if f(Po) f(P) for all point P near Po. How will these ideas translate for f(x, y)? ?

Local Extrema Recall: f has a local maximum at the point Po, if f(Po) f(P) for all point P near Po. f has a local minimum at the point Po, if f(Po) f(P) for all point P near Po. The gradient of f serves the same function for f(x, y) as f'(x) did for x. Recall that grad f points in the direction of greatest increase of f. What does this mean if Po is a local max?

Local Extrema Examine Fig 14. 1 and 14. 2 pg 176. You can see the local maxima and minima in Fig. 14. 1. How do they appear in the contour diagram in Fig 14. 2? ? Can you see as you get closer and closer to a local extrema, the contour lines get closer and closer together until what happens?

Local Extrema The condition for finding the critical points is for For grad f to be zero, what must be true?

Local Extrema The condition for finding the critical points is for For grad f to be zero, what must be true? This means that each partial derivative must be zero. Example 1, 2 pg 177 -178. Note how the local min/max are found.

Local Extrema The condition for finding the critical points is for Find the critical points of the function: