How derivatives affect the shape of a graph

How derivatives affect the shape of a graph (Section 4. 3) Alex Karassev

First and second derivatives l l f ′ tells us about intervals of increase and decrease f ′′ tells us about concavity

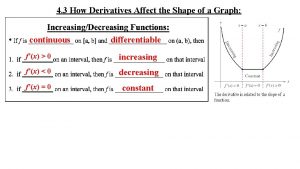
First derivative: Intervals of Increase / Decrease

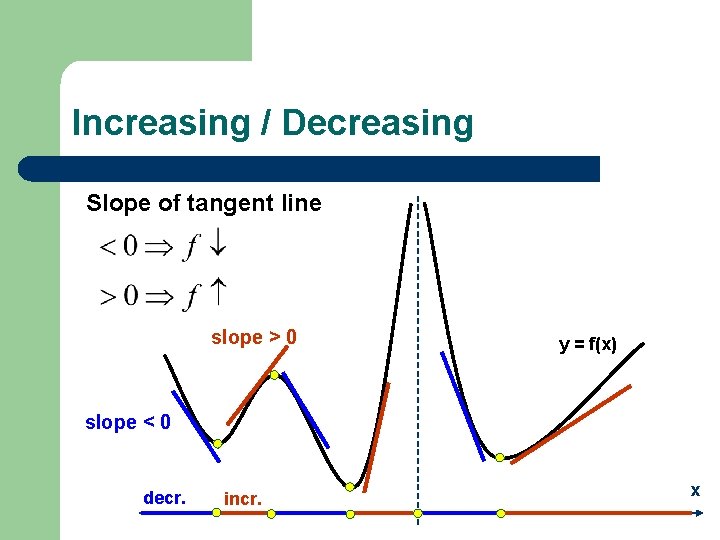
Increasing / Decreasing Slope of tangent line slope > 0 y = f(x) slope < 0 decr. incr. x

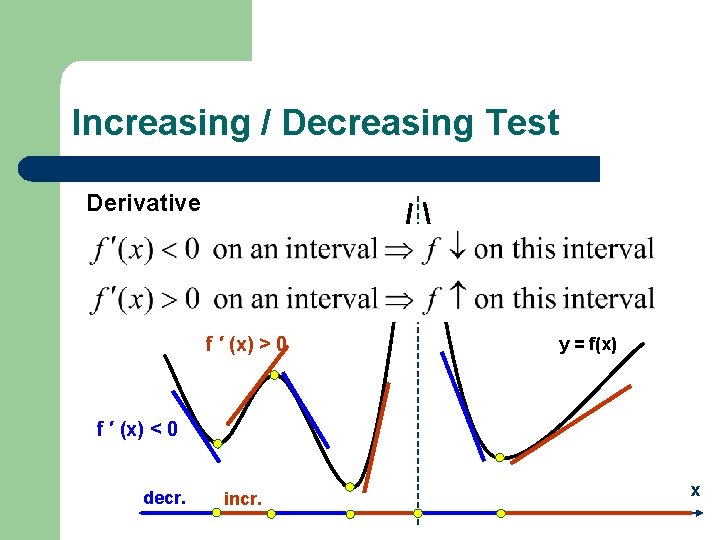
Increasing / Decreasing Test Derivative f ′ (x) > 0 y = f(x) f ′ (x) < 0 decr. incr. x

Change of behavior f can change from increasing to decreasing and vice versa: • at the points of local max/min (i. e. at the critical numbers) • at the points where f is undefined f ′ (x) > 0 y = f(x) f ′ (x) < 0 decr. incr. x

Local max/min: 1 st derivative test loc. max loc. min. f ′ (x) < 0 decr. y = f(x) l Let c be a critical number l How do we determine whether it is loc. min or loc. max or neither? f ′ (x) > 0 c incr. x l If f ′ changes from negative to positive at c, it is loc. min. l If f ′ changes from positive to negative at c, it is loc. max. l If f ′ does not change sign at c, it is neither (e. g. f(x) = x 3, c =0)

Second derivative: Concavity

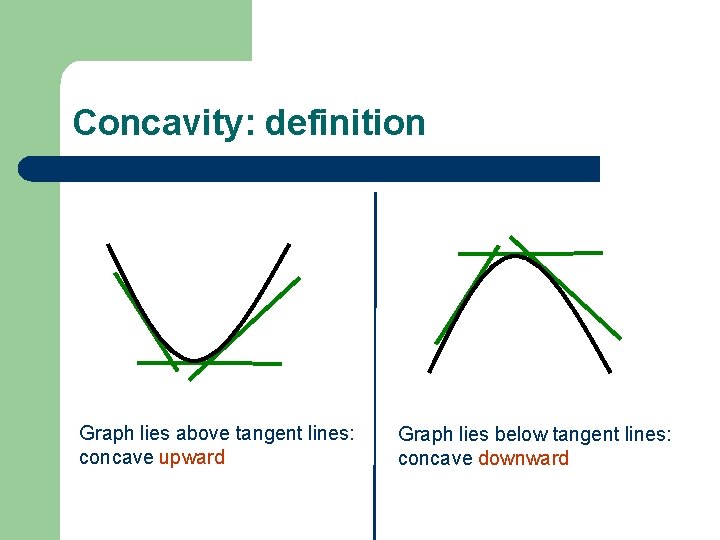
Concavity: definition Graph lies above tangent lines: concave upward Graph lies below tangent lines: concave downward

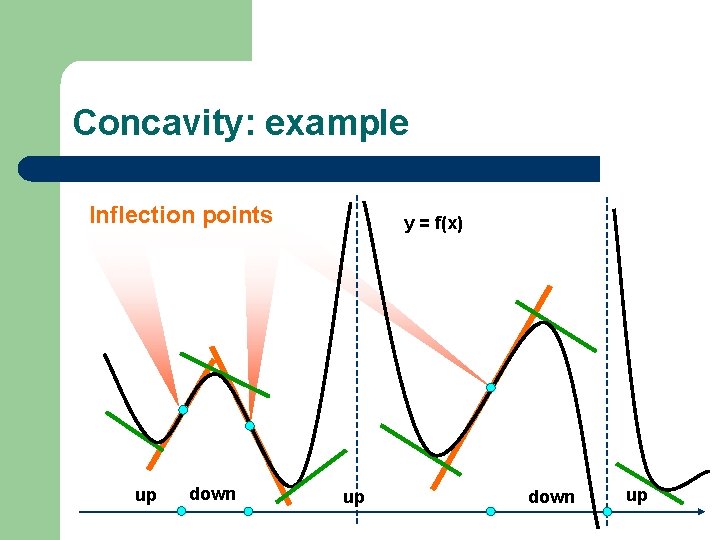
Concavity: example Inflection points up down y = f(x) up down up

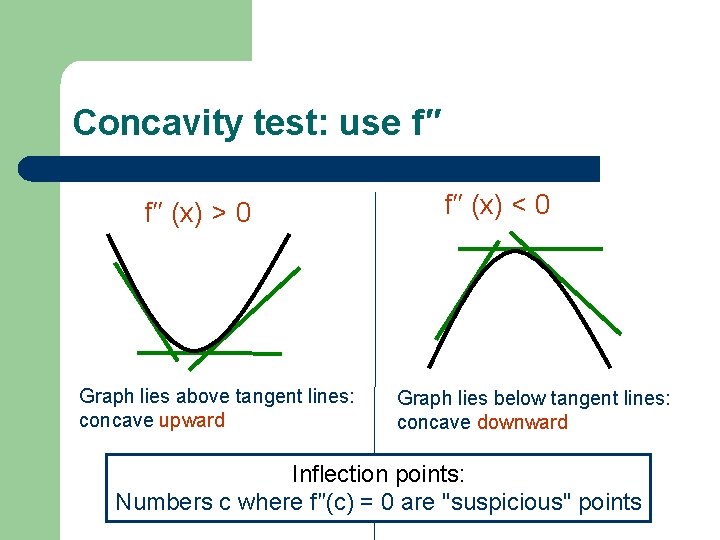
Concavity test: use f′′ (x) > 0 Graph lies above tangent lines: concave upward f′′ (x) < 0 Graph lies below tangent lines: concave downward Inflection points: Numbers c where f′′(c) = 0 are "suspicious" points

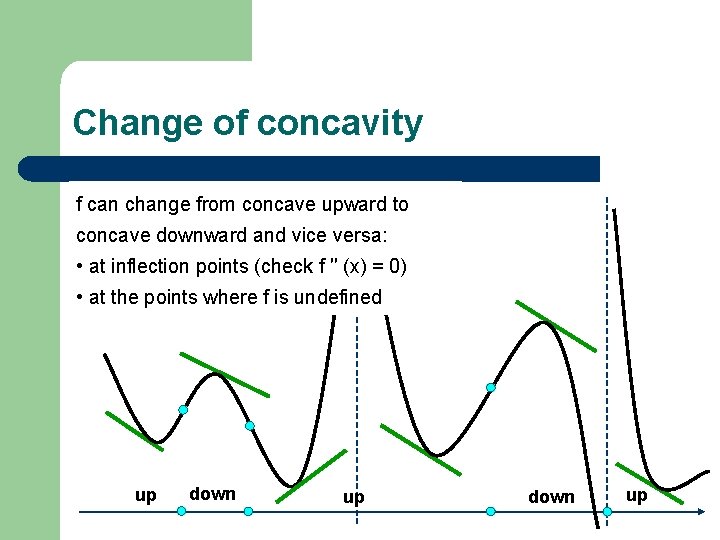
Change of concavity f can change from concave upward to concave downward and vice versa: • at inflection points (check f ′′ (x) = 0) y = f(x) • at the points where f is undefined up down up

Local max/min: 2 nd derivative test loc. max f ′′ (c) < 0 loc. min. f ′′ (c) > 0 c y = f(x) x l Suppose f ′ (c) = 0 l How do we determine whether it is loc. min or loc. max or neither? NOTE: tangent line at (c, f(c)) is horizontal l ⇒ loc. min. If f ′′ (c) < 0 the graph lies below the tangent ⇒ loc. max. l If f ′′ (c) = 0 the test is inconclusive (use 1 st deriv. test instead!) l If f ′′ (c) > 0 the graph lies above the tangent

Comparison of 1 st and 2 nd derivative tests for local max/min l Second derivative test is faster then 1 st derivative test (we need to determine where f′(c) = 0 and then just compute f′′(c) at each such c) l Second derivative test can be generalized on the case of functions of several variables l However, when f′′(c) = 0, the second derivative test is inconclusive (for example, (0, 0) is an inflection point for f(x) = x 3, while for x 4 it is a point of local minimum, and for –x 4 it is a point of local maximum)

Examples l l Sketch the graph of function y = x 4 – 6 x 2 Use the second derivative test to find points of local maximum and minimum of f(x) = x/(x 2+4)