Cap 11 I Quadrilateri Definizione di quadrilatero Si




















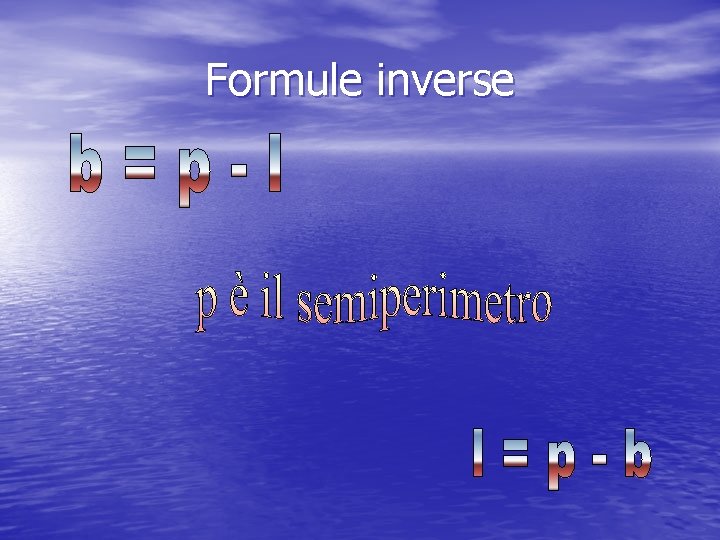
















- Slides: 64

Cap. 11 I Quadrilateri

Definizione di quadrilatero Si definisce quadrilatero un poligono di 4 lati

Definizione di poligono Definiamo poligono una porzione di piano delimitata da una spezzata chiusa

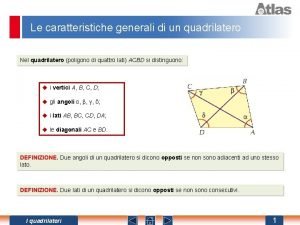
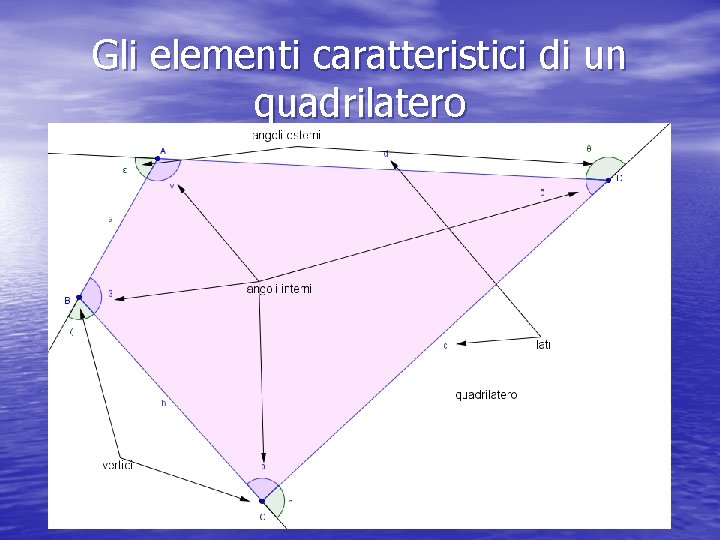
Gli elementi caratteristici di un quadrilatero

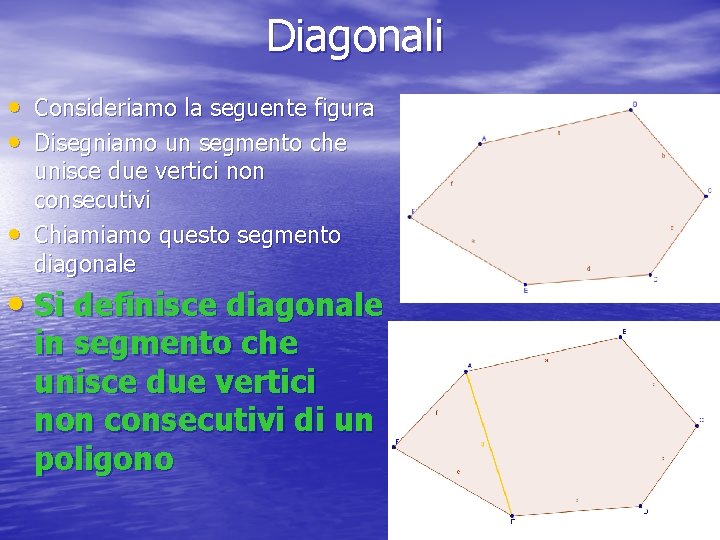
Diagonali • Consideriamo la seguente figura • Disegniamo un segmento che • unisce due vertici non consecutivi Chiamiamo questo segmento diagonale • Si definisce diagonale in segmento che unisce due vertici non consecutivi di un poligono

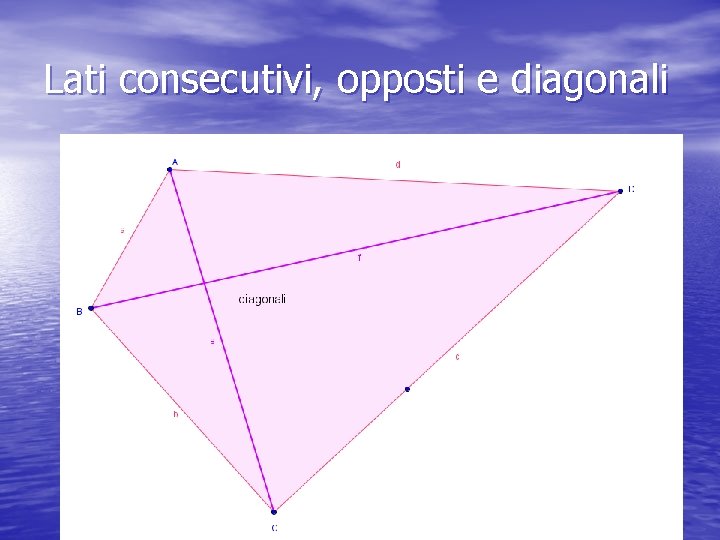
Lati consecutivi, opposti e diagonali

Definizioni nei quadrilateri • Due vertici si dicono consecutivi se • • • appartengono allo stesso lato Due vertici si dicono opposti se non hanno nessun lato in comune Due lati si dicono consecutivi se hanno un vertice in comune Due lati si dicono opposti se non hanno vertici in comune Due angoli si dicono adiacenti se hanno un lato in comune Due angoli si dicono opposti se non hanno nessun lato in comune


Somma degli angoli interni di un quadrilatero i l g e d a m m o S = i n r e t n i i l 0 ango 8 1 x 2 – 0 8 lx 1 La somma degli angoli interni di Da cui un quadrilatero vale (4 -2) x 180° i l g e d cioè 2 x 180° = 360° a m m o S = i n r e t n i angoli 0 8 1 x ) (l – 2 In un quadrilatero l = 4 perciò

Criterio di esistenza di un poligono • Consideriamo tre segmenti • È sempre possibile costruire un • • • poligono? In teoria sembrerebbe di si perché posso metterli l’altro Inuno undietro poligono un Ma il giochetto riesce sempre? lato deve essere Consideriamo altri tre segmenti Ripetiamo minore l’operazione della somma Come si vede non diposso tutticostruire gli altri un poligono, uno dei due segmenti è addirittura più grande della somma degli altri due

Criterio di esistenza dei quadrilateri In un quadrilatero un lato deve essere minore della somma di tutti gli altri

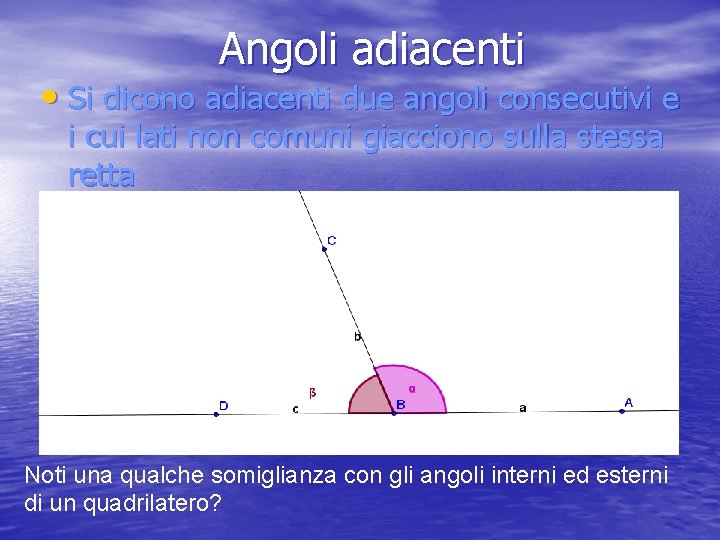
Angoli adiacenti • Si dicono adiacenti due angoli consecutivi e i cui lati non comuni giacciono sulla stessa retta Noti una qualche somiglianza con gli angoli interni ed esterni di un quadrilatero?

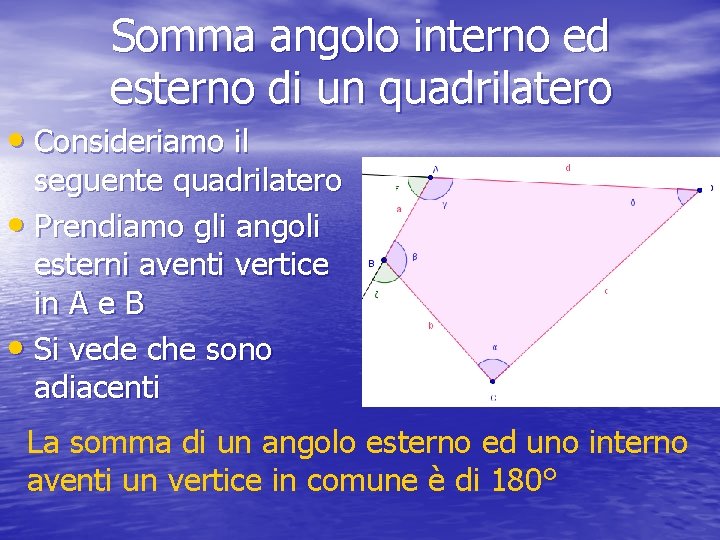
Somma angolo interno ed esterno di un quadrilatero • Consideriamo il seguente quadrilatero • Prendiamo gli angoli esterni aventi vertice in A e B • Si vede che sono adiacenti La somma di un angolo esterno ed uno interno aventi un vertice in comune è di 180°

Perimetro di un quadrilatero • Consideriamo il seguente quadrilatero • I lati a, b, c, e d rappresenteranno il contorno del quadrilatero • Immaginiamo ora di prenderli uno ad uno e di sommarli • (sappiamo già come si fa) La lunghezza del segmento A’A’’ ottenuto sommando questi lati è detta perimetro del quadrilatero • Di definisce perimetro di un quadrilatero e si indica con 2 P la misura del contorno del quadrilatero

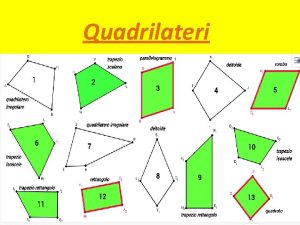
Quadrilateri particolari • Alcuni quadrilateri si contraddistinguono per avere delle proprietà particolari • Questi quadrilateri hanno dei nomi particolari e proprietà che noi ci accingiamo a scoprire

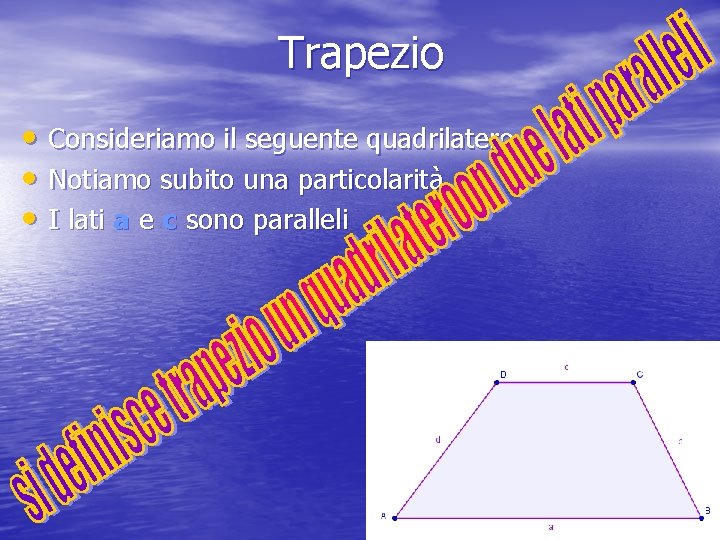
Trapezio • Consideriamo il seguente quadrilatero • Notiamo subito una particolarità • I lati a e c sono paralleli

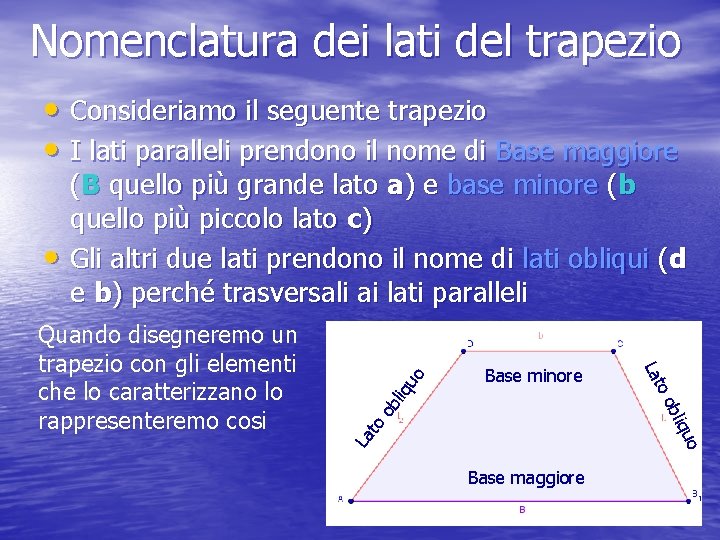
Nomenclatura dei lati del trapezio • Consideriamo il seguente trapezio • I lati paralleli prendono il nome di Base maggiore u bliq ob liq oo uo Base minore Lat Quando disegneremo un trapezio con gli elementi che lo caratterizzano lo rappresenteremo cosi o La to • (B quello più grande lato a) e base minore (b quello più piccolo lato c) Gli altri due lati prendono il nome di lati obliqui (d e b) perché trasversali ai lati paralleli Base maggiore

Distanza fra due rette parallele • Consideriamo due rette parallele r • • • ed s appartenenti al piano a Tracciamo la perpendicolare alla retta r ed s Tale retta taglierà le due rette parallele nei punti A e B Si dice distanza fra le due rette la lunghezza del segmento AB perché è perpendicolare ad entrambe le rette t A s B r Distanza fra rette parallele Si definisce distanza di due rette parallele la lunghezza del segmento perpendicolare alle rette date e che ha come suoi estremi punti appartenenti alle due rette a

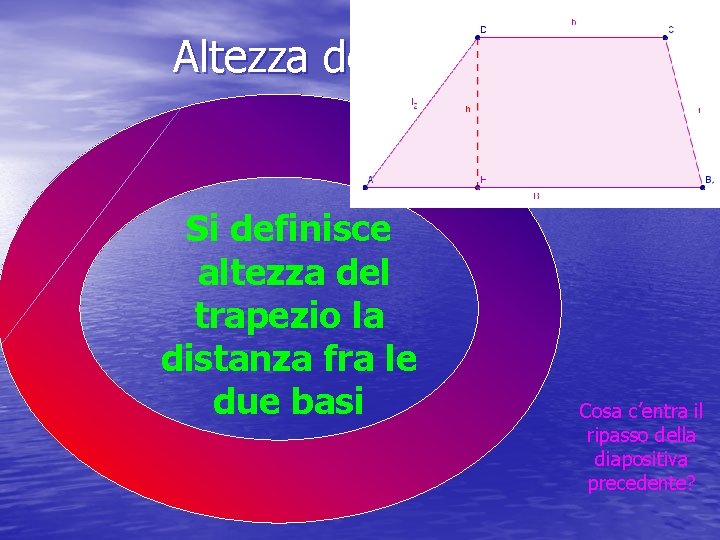
Altezza del trapezio Si definisce altezza del trapezio la distanza fra le due basi Cosa c’entra il ripasso della diapositiva precedente?

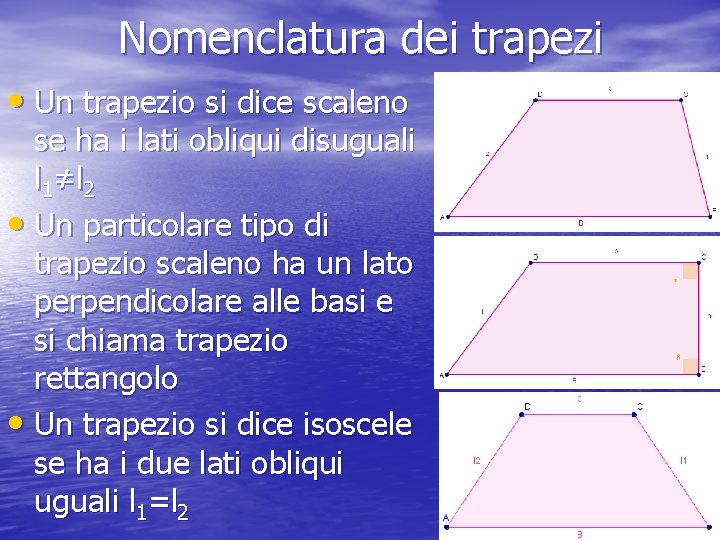
Nomenclatura dei trapezi • Un trapezio si dice scaleno se ha i lati obliqui disuguali l 1≠l 2 • Un particolare tipo di trapezio scaleno ha un lato perpendicolare alle basi e si chiama trapezio rettangolo • Un trapezio si dice isoscele se ha i due lati obliqui uguali l 1=l 2

Proiezione di un segmento su una retta • Consideriamo una retta r e una • • segmento P appartenenti entrambi al piano a Per proiettare in segmento sulla retta basta proiettare i suoi estremi sulla retta r Troviamo i punti A’ e B’ B A A’ • Il segmento A’B’ sarà la proiezione di AB su r Per proiettare un segmento su una retta basta trovare le proiezioni dei suoi due punti estremi e prendere in considerazione il segmento risultante B’ r a

Proiezione dei lati obliqui sulla base maggiore • Consideriamo un trapezio • Dai vertici della base minore • • tracciamo le perpendicolari alla base maggiore Queste incontrano nei punti H e. K Per definizione di proiezione di un segmento su una retta …. I segmenti AH e BK saranno le proiezioni dei lati obliqui sulla base

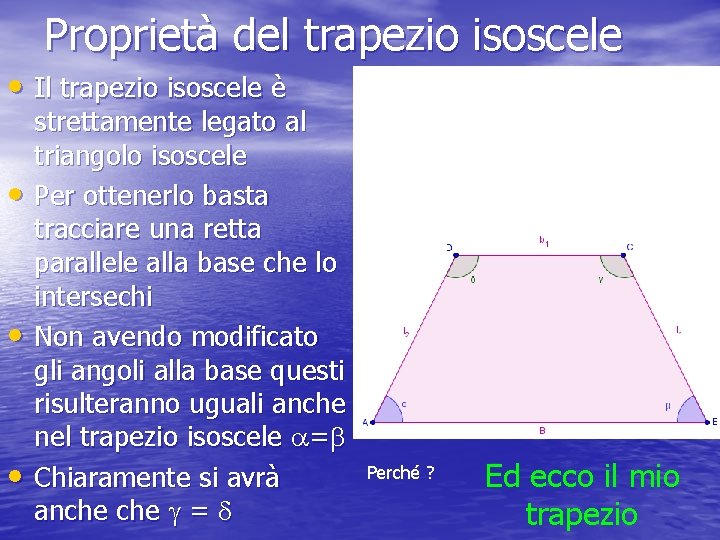
Proprietà del trapezio isoscele • Il trapezio isoscele è • • • strettamente legato al triangolo isoscele Per ottenerlo basta tracciare una retta parallele alla base che lo intersechi Non avendo modificato gli angoli alla base questi risulteranno uguali anche nel trapezio isoscele a=b Chiaramente si avrà anche g = d Perché ? Ed ecco il mio trapezio

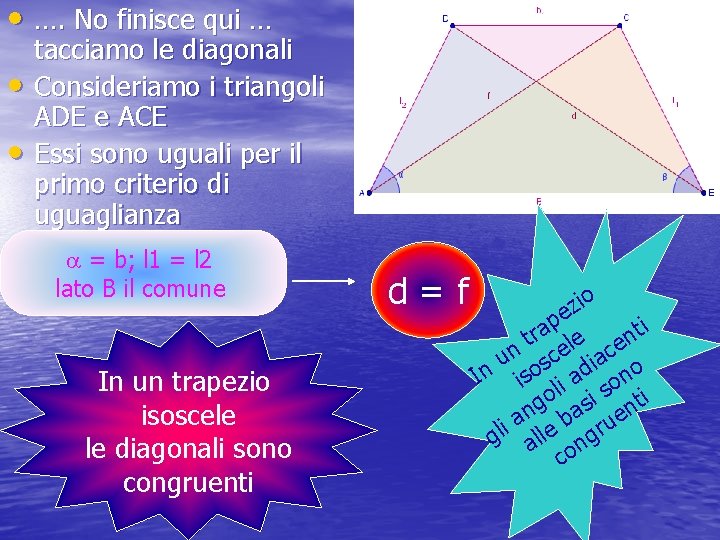
• …. No finisce qui … • • tacciamo le diagonali Consideriamo i triangoli ADE e ACE Essi sono uguali per il primo criterio di uguaglianza a = b; l 1 = l 2 lato B il comune In un trapezio isoscele le diagonali sono congruenti d=f io z e p i tra ele ent un osc diac o In is li a on o si s ti g n ba en a u gli alle ngr co

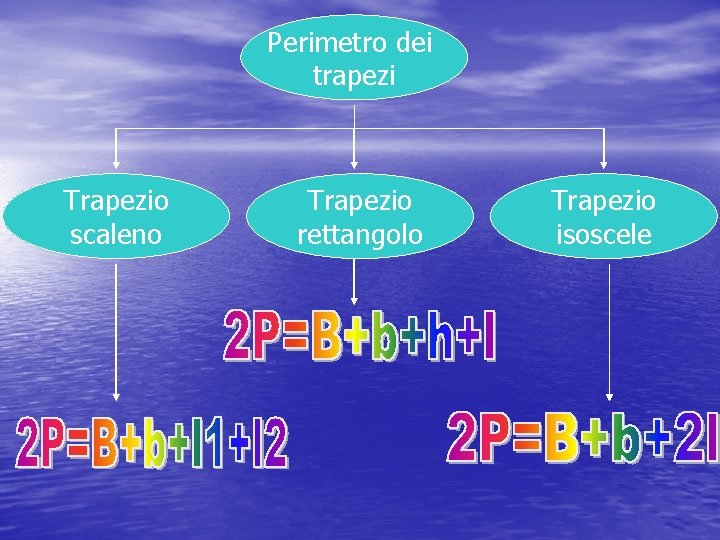
Perimetro dei trapezi Trapezio scaleno Trapezio rettangolo Trapezio isoscele


Parallelogramma • Consideriamo il seguente • trapezio Spostiamo pi punto D fino a far diventare d parallelo a b Otteniamo una figura con i lati opposti paralleli e congruenti Un parallelogramma è un trapezio? Pensa alla definizione di trapezio Pensa a ciò che è stato fatto per ottenere un trapezio

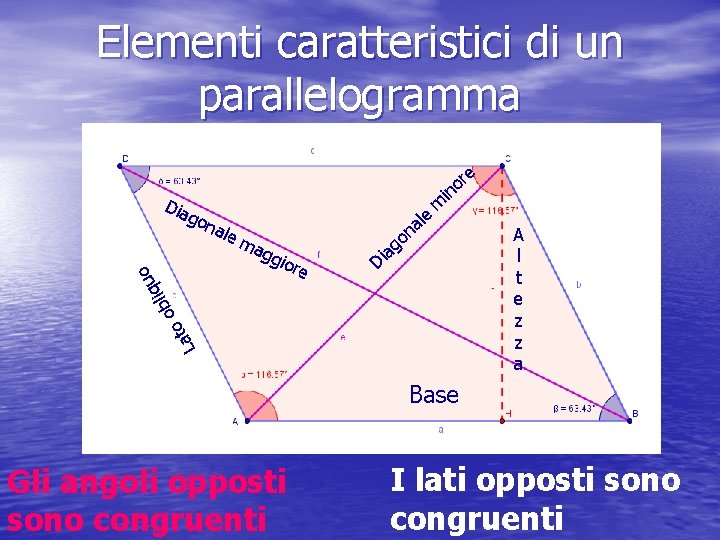
Elementi caratteristici di un parallelogramma Dia ale m agg iore a Di a n go le m La t uo q i bl o o gon re o in A l t e z z a Base Gli angoli opposti sono congruenti I lati opposti sono congruenti

In un parallelogramma i lati e gli angoli opposti sono congruenti e gli angoli adiacenti a ciascun lato sono supplementari

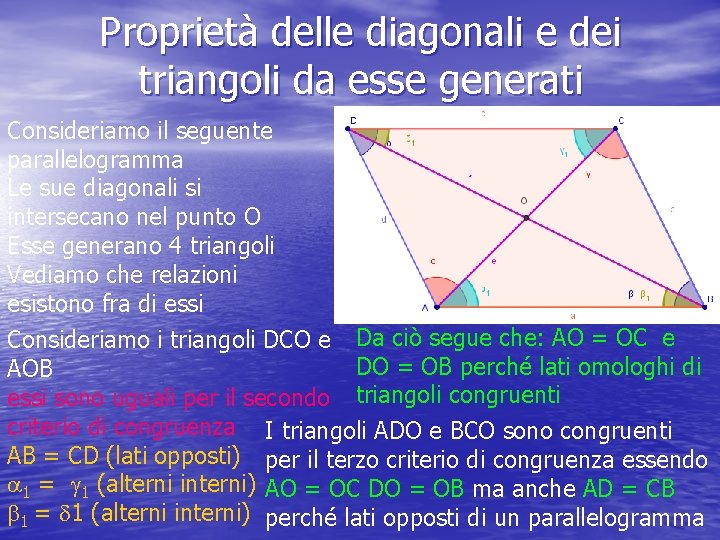
Proprietà delle diagonali e dei triangoli da esse generati Consideriamo il seguente parallelogramma Le sue diagonali si intersecano nel punto O Esse generano 4 triangoli Vediamo che relazioni esistono fra di essi Consideriamo i triangoli DCO e Da ciò segue che: AO = OC e DO = OB perché lati omologhi di AOB essi sono uguali per il secondo triangoli congruenti criterio di congruenza I triangoli ADO e BCO sono congruenti AB = CD (lati opposti) per il terzo criterio di congruenza essendo a 1 = g 1 (alterni interni) AO = OC DO = OB ma anche AD = CB b 1 = d 1 (alterni interni) perché lati opposti di un parallelogramma

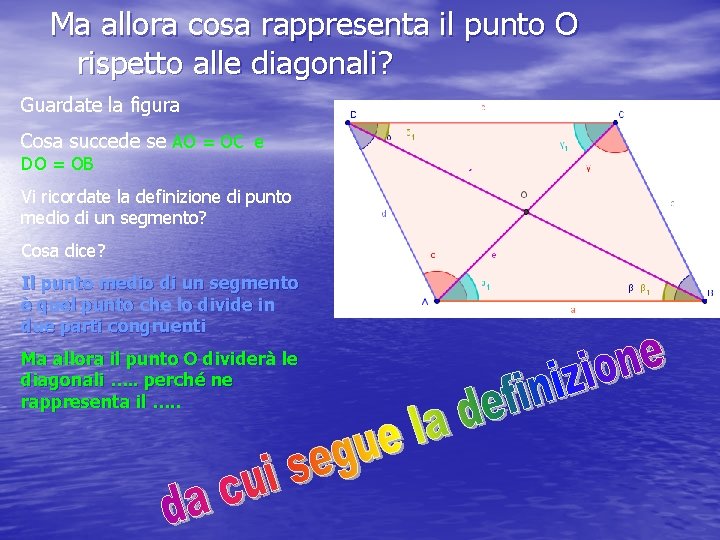
Ma allora cosa rappresenta il punto O rispetto alle diagonali? Guardate la figura Cosa succede se AO = OC e DO = OB Vi ricordate la definizione di punto medio di un segmento? Cosa dice? Il punto medio di un segmento è quel punto che lo divide in due parti congruenti Ma allora il punto O dividerà le diagonali …. . perché ne rappresenta il …. .

Le diagonali di un parallelogrammo si incontrano nel loro punto medio Cioè il punto di incidenza le divide a metà

Quante altezze ha un parallelogramma • Il concetto di altezza rimanda direttamente a quello della distanza di in punto da una retta ve lo ricordate …. . • La distanza di un punto da una retta è data dalla lunghezza del segmento perpendicolare che unisce il punto alla retta • Perciò l’altezza è la lunghezza del segmento perpendicolare che unisce un punto al lato opposto

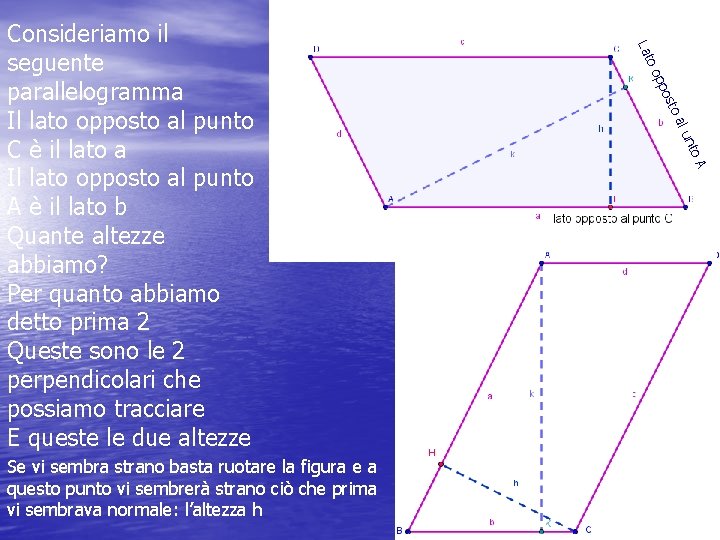
sto ppo oo to n al u A Se vi sembra strano basta ruotare la figura e a questo punto vi sembrerà strano ciò che prima vi sembrava normale: l’altezza h Lat Consideriamo il seguente parallelogramma Il lato opposto al punto C è il lato a Il lato opposto al punto A è il lato b Quante altezze abbiamo? Per quanto abbiamo detto prima 2 Queste sono le 2 perpendicolari che possiamo tracciare E queste le due altezze

…. . È un’operazione ammissibile ruotare una figura? Ricordiamo la definizione di geometria Che tipo di operazione abbiamo fatto? Una trasformazione si dice isometrica quando lascia inalterata la figura Una trasformazione e precisamente una trasformazione isometrica

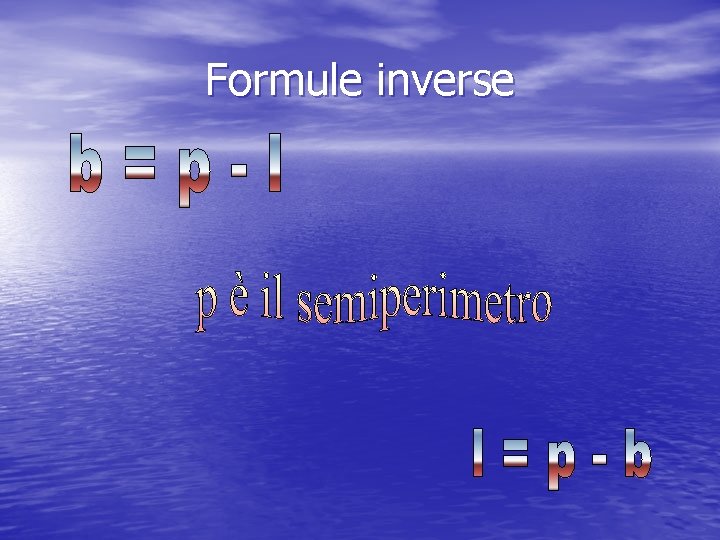
Formule inverse

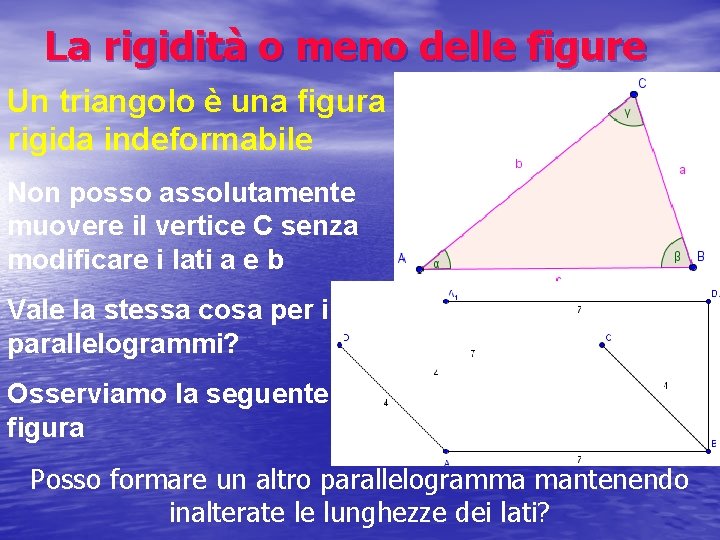
La rigidità o meno delle figure Un triangolo è una figura rigida indeformabile Non posso assolutamente muovere il vertice C senza modificare i lati a e b Vale la stessa cosa per i parallelogrammi? Osserviamo la seguente figura Posso formare un altro parallelogramma mantenendo inalterate le lunghezze dei lati?

La risposta è si e le figure che posso ottenere sono infinite I parallelogrammi non sono figure rigide

Il rettangolo Se osserviamo la seguente figura ci rendiamo conto che il rettangolo non è altro che un particolare tipo parallelogramma Che caratteristiche ha questo parallelogramma? Come possiamo vedere ha tutti gli angoli retti Il rettangolo è un trapezio ?

Si dice rettangolo un parallelogramma equiangolo

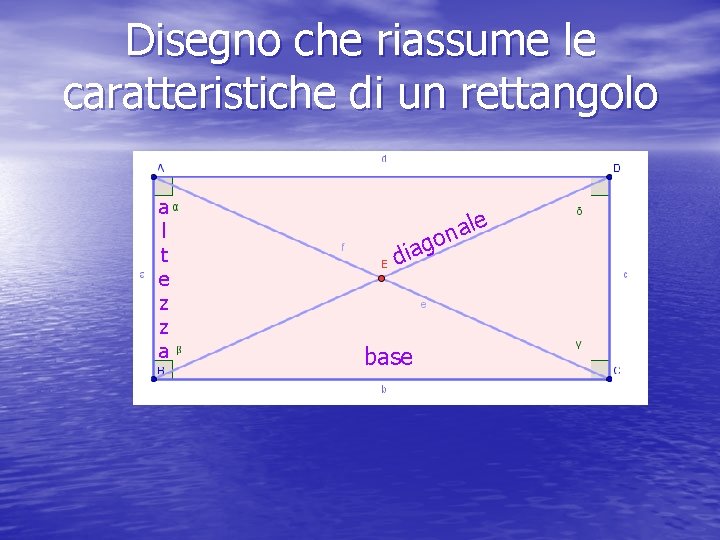
Disegno che riassume le caratteristiche di un rettangolo a l t e z z a le a n go dia base

Proprietà delle diagonali e dei triangoli da esse generati È dato il seguente rettangolo Prendiamo in considerazione i triangoli BAC e DBC Essi sono congruenti per il primo criterio di congruenza perché: a = c lati opposti la base b è in comune b = g perché retti Perciò si ha che BD = AC perché lati omologhi di triangoli congruenti

Le diagonali di un rettangolo sono congruenti

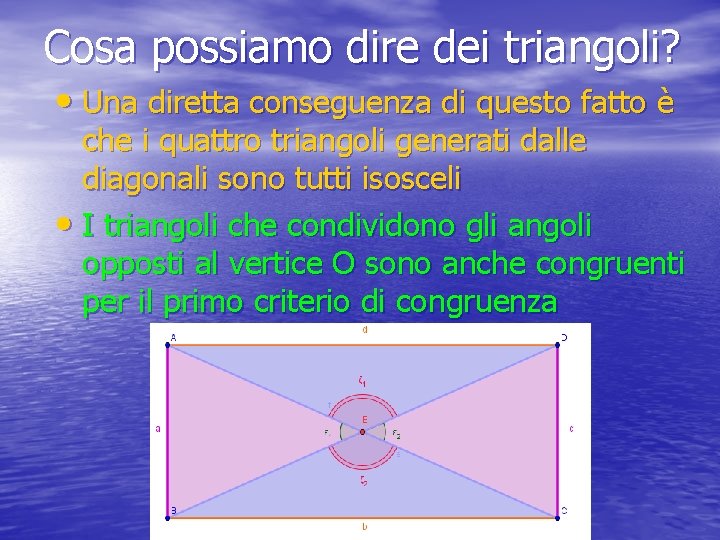
Cosa possiamo dire dei triangoli? • Una diretta conseguenza di questo fatto è che i quattro triangoli generati dalle diagonali sono tutti isosceli • I triangoli che condividono gli angoli opposti al vertice O sono anche congruenti per il primo criterio di congruenza


Formule inverse

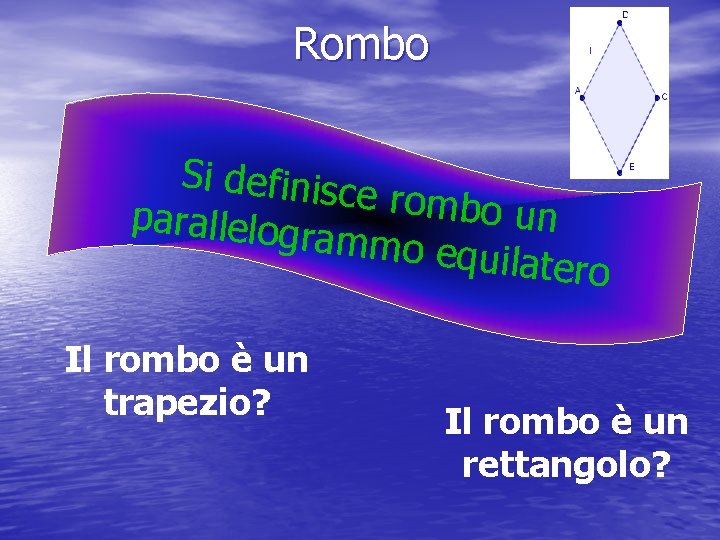
Rombo Si definisc e rombo u parallelog n rammo eq uilatero Il rombo è un trapezio? Il rombo è un rettangolo?

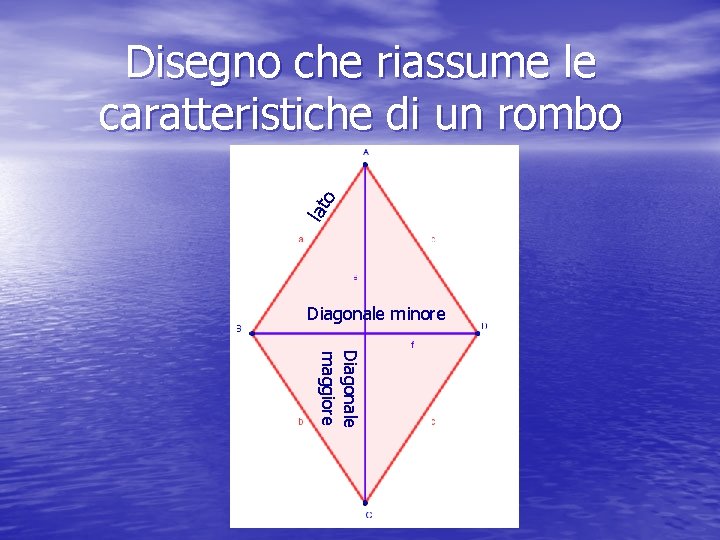
lat o Disegno che riassume le caratteristiche di un rombo Diagonale minore Diagonale maggiore

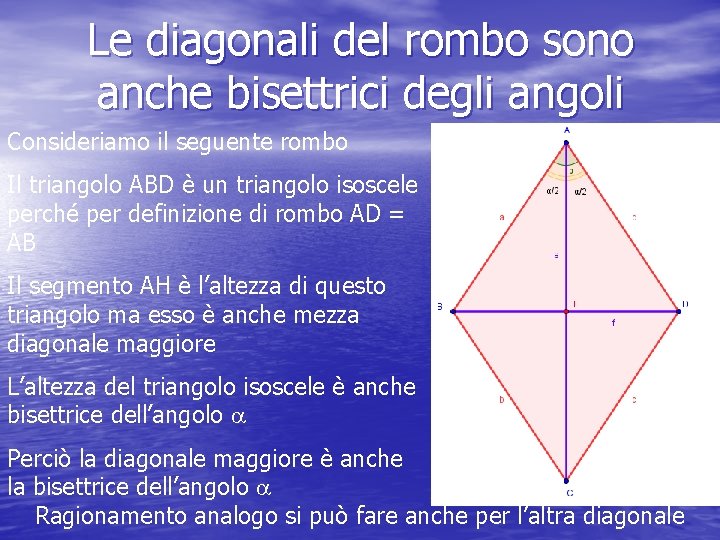
Le diagonali del rombo sono anche bisettrici degli angoli Consideriamo il seguente rombo Il triangolo ABD è un triangolo isoscele perché per definizione di rombo AD = AB Il segmento AH è l’altezza di questo triangolo ma esso è anche mezza diagonale maggiore L’altezza del triangolo isoscele è anche bisettrice dell’angolo a Perciò la diagonale maggiore è anche la bisettrice dell’angolo a Ragionamento analogo si può fare anche per l’altra diagonale

Le diagonali di un rombo lo dividono in 4 parti congruenti Riprendiamo l’immagine precedente I triangoli ABH e AHD sono congruenti per il primo criterio perché: AB = AD perché lati di un rombo Siccome i quattro triangoli AH è il comune sono congruenti le diagonali di b = g perché bisettrici di uno stesso un rombo lo dividono in angolo 4 parti uguali Lo stesso ragionamento può essere fatto per le coppie di triangoli AHD e CHD; CHD e BHC; BHC e BHA

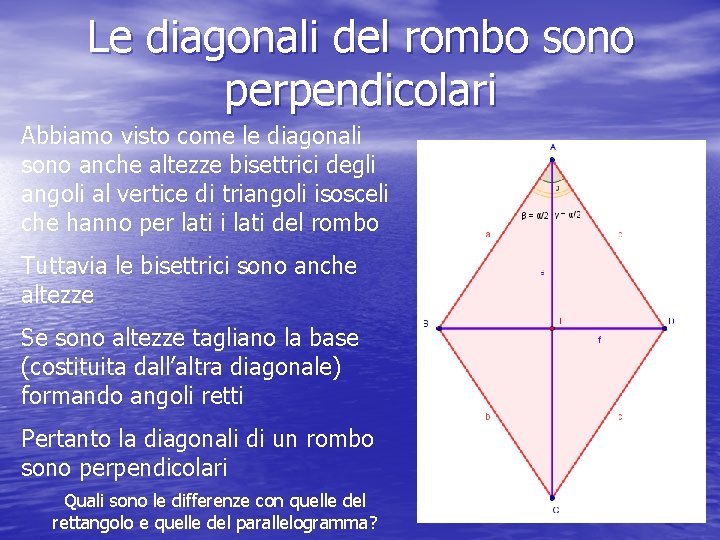
Le diagonali del rombo sono perpendicolari Abbiamo visto come le diagonali sono anche altezze bisettrici degli angoli al vertice di triangoli isosceli che hanno per lati i lati del rombo Tuttavia le bisettrici sono anche altezze Se sono altezze tagliano la base (costituita dall’altra diagonale) formando angoli retti Pertanto la diagonali di un rombo sono perpendicolari Quali sono le differenze con quelle del rettangolo e quelle del parallelogramma?

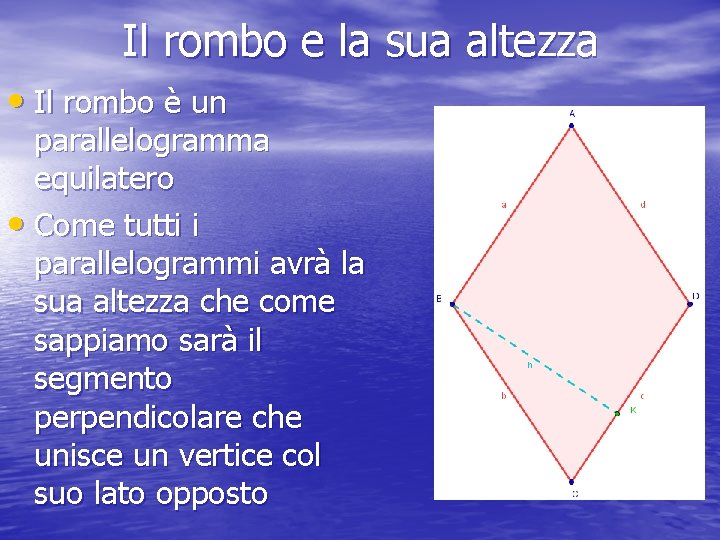
Il rombo e la sua altezza • Il rombo è un parallelogramma equilatero • Come tutti i parallelogrammi avrà la sua altezza che come sappiamo sarà il segmento perpendicolare che unisce un vertice col suo lato opposto


Formula inversa

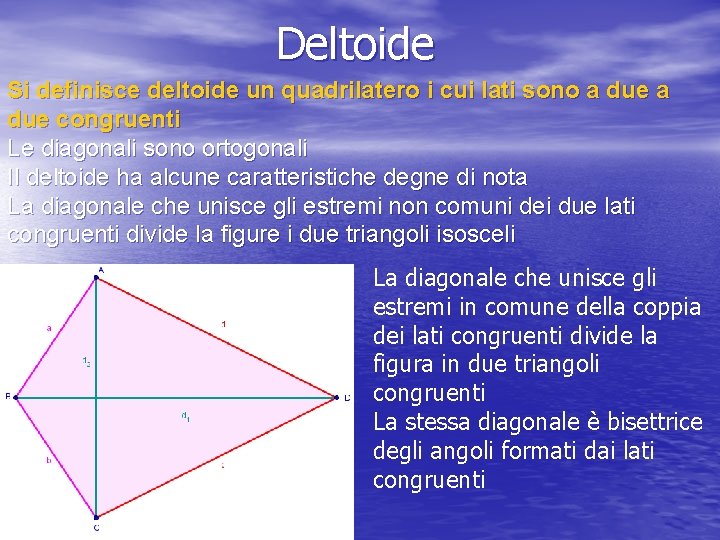
Deltoide Si definisce deltoide un quadrilatero i cui lati sono a due congruenti Le diagonali sono ortogonali Il deltoide ha alcune caratteristiche degne di nota La diagonale che unisce gli estremi non comuni dei due lati congruenti divide la figure i due triangoli isosceli La diagonale che unisce gli estremi in comune della coppia dei lati congruenti divide la figura in due triangoli congruenti La stessa diagonale è bisettrice degli angoli formati dai lati congruenti

Il quadrato Si definisce quadrato un parallelogramma equilatero ed equiangolo

Caratteristiche del quadrato Come il rettangolo il quadrato ha gli angoli e le diagonali congruenti Come il rombo il quadrato ha i lati congruenti e le diagonali fra loro perpendicolari e bisettrici degli angoli

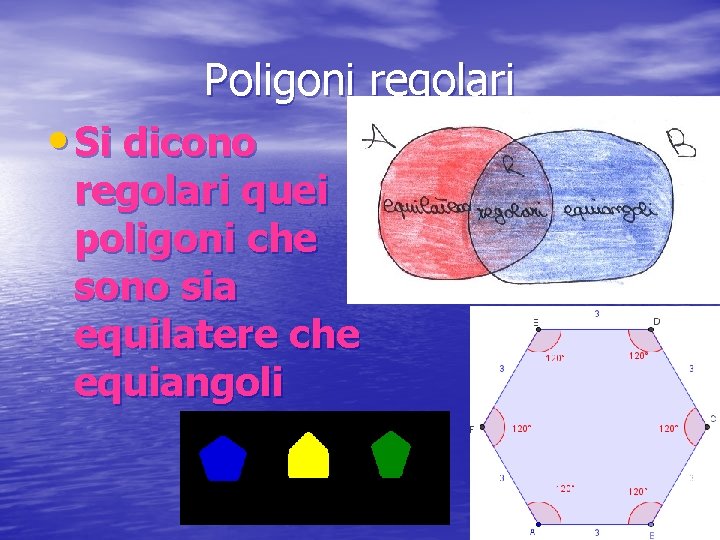
Poligoni regolari • Si dicono regolari quei poligoni che sono sia equilatere che equiangoli

Si perché è sia equilatero che equiangolo


Formula del perimetro del quadrato

Formula inversa

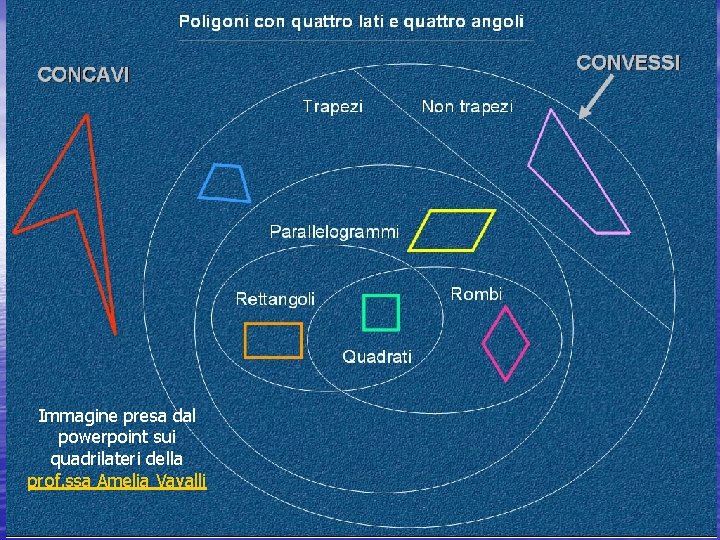
Immagine presa dal powerpoint sui quadrilateri della prof. ssa Amelia Vavalli
 Quadrilatero definizione
Quadrilatero definizione Cap compas
Cap compas Beregning af hcp resultat
Beregning af hcp resultat Quais das figuras não são polígonos
Quais das figuras não são polígonos Paralelogramos
Paralelogramos Quadrilatero austriaco
Quadrilatero austriaco Quadrilateri non regolari
Quadrilateri non regolari Homoteria
Homoteria Escudos cristalinos
Escudos cristalinos Quadrilatero birettangolo isoscele
Quadrilatero birettangolo isoscele Famiglia dei parallelogrammi
Famiglia dei parallelogrammi Quadrilatero irregolare
Quadrilatero irregolare Quadriltero
Quadriltero Diagramma quadrilateri
Diagramma quadrilateri Observe o quadrilátero abcd abaixo
Observe o quadrilátero abcd abaixo Quadrilatero ferrifero
Quadrilatero ferrifero Exemplos de quadriláteros
Exemplos de quadriláteros Teorema poligoni circoscritti
Teorema poligoni circoscritti Caratteristiche dei quadrilateri
Caratteristiche dei quadrilateri Trapezi classificazione
Trapezi classificazione Problemi con i quadrilateri
Problemi con i quadrilateri Significato di equiesteso
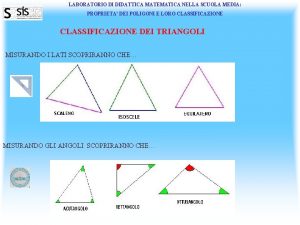
Significato di equiesteso Laboratori matematica scuola media
Laboratori matematica scuola media Oggetti a forma di rettangolo
Oggetti a forma di rettangolo Trapezi scuola primaria
Trapezi scuola primaria Polar ice cap biome
Polar ice cap biome Brain swim cap activity
Brain swim cap activity Cap 5415
Cap 5415 Cap root word examples
Cap root word examples Certified analytics professional cap
Certified analytics professional cap Cap height
Cap height Spore fps cap
Spore fps cap Total cap 2
Total cap 2 Idrolisi salina
Idrolisi salina Hydroxyzine pam 50 mg cap for anxiety
Hydroxyzine pam 50 mg cap for anxiety Alarmplattform
Alarmplattform Meltem seli
Meltem seli Kaput suksedenum
Kaput suksedenum What type of simple machine is an ax
What type of simple machine is an ax Design of parapet wall
Design of parapet wall Database technologies
Database technologies Topside cap on
Topside cap on Cap rate sensitivity analysis
Cap rate sensitivity analysis Cap microservices
Cap microservices Be cap
Be cap La princesa es malvada cap 19
La princesa es malvada cap 19 Unromantic cap 55
Unromantic cap 55 Thin cap rules
Thin cap rules Fibroscan valore f4
Fibroscan valore f4 Cap paulo
Cap paulo Stempel perpustakaan sekolah
Stempel perpustakaan sekolah Pvu official announcement
Pvu official announcement Betacap 30
Betacap 30 Cap building systems
Cap building systems Ics team leader
Ics team leader Cap form 91
Cap form 91 Rapport de stage cap
Rapport de stage cap Block xoang nhĩ độ 2 type 1
Block xoang nhĩ độ 2 type 1 Cap module
Cap module Origin of species manhwa chapter 24
Origin of species manhwa chapter 24 Malcolm kyser
Malcolm kyser Where is my cap
Where is my cap La metamorfosis capitulo 1
La metamorfosis capitulo 1 Teorema de cap
Teorema de cap Af blues
Af blues