Geometria plana ndice Polgonos Tringulos Congruncia de tringulos

Geometria plana Índice Polígonos Triângulos Congruência de triângulos Semelhança de triângulos Relações métricas no triângulo retângulo Quadriláteros Teorema de Tales Esquadros de madeira ― www. ser. com. br Teorema da bissetriz de um ângulo interno de um triângulo 1

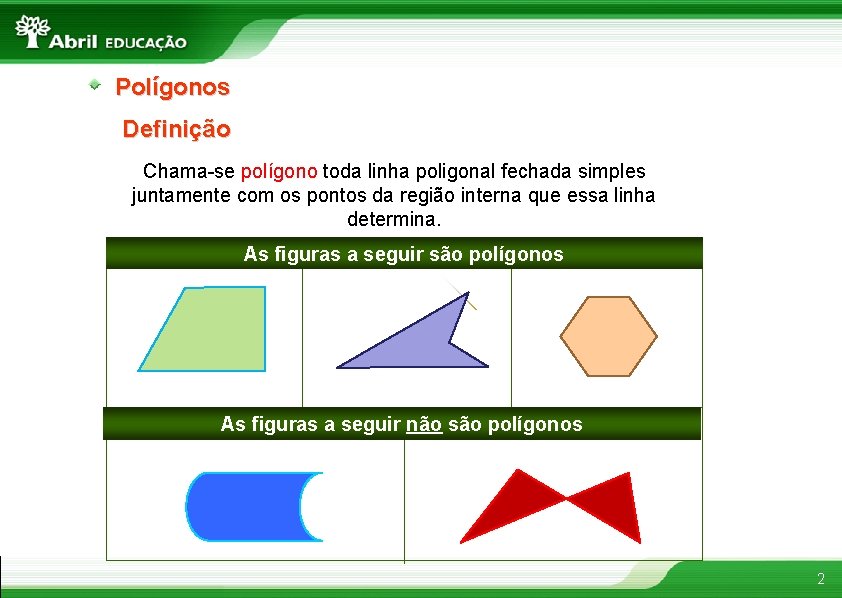
Polígonos Definição Chama-se polígono toda linha poligonal fechada simples juntamente com os pontos da região interna que essa linha determina. As figuras a seguir são polígonos As figuras a seguir não são polígonos 2

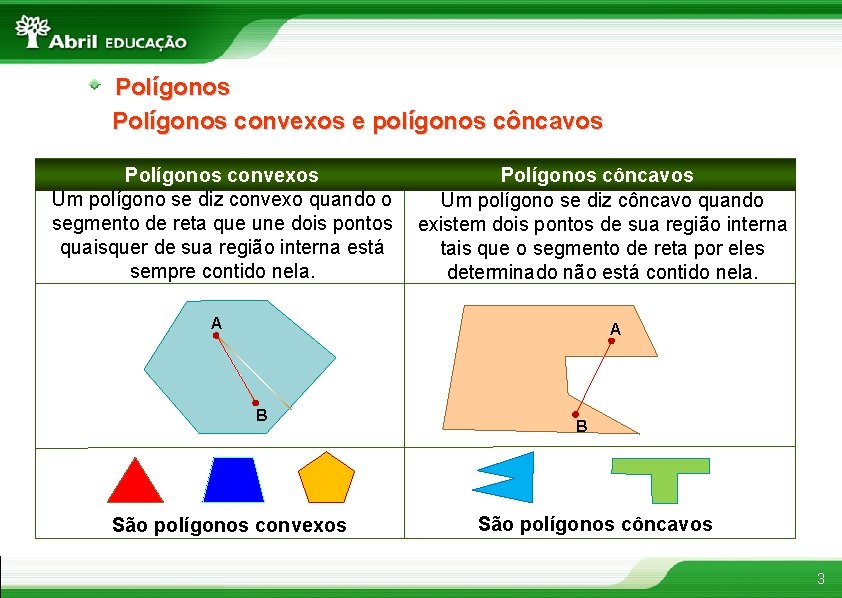
Polígonos convexos e polígonos côncavos Polígonos convexos Um polígono se diz convexo quando o segmento de reta que une dois pontos quaisquer de sua região interna está sempre contido nela. Polígonos côncavos Um polígono se diz côncavo quando existem dois pontos de sua região interna tais que o segmento de reta por eles determinado não está contido nela. A A B São polígonos convexos B São polígonos côncavos 3

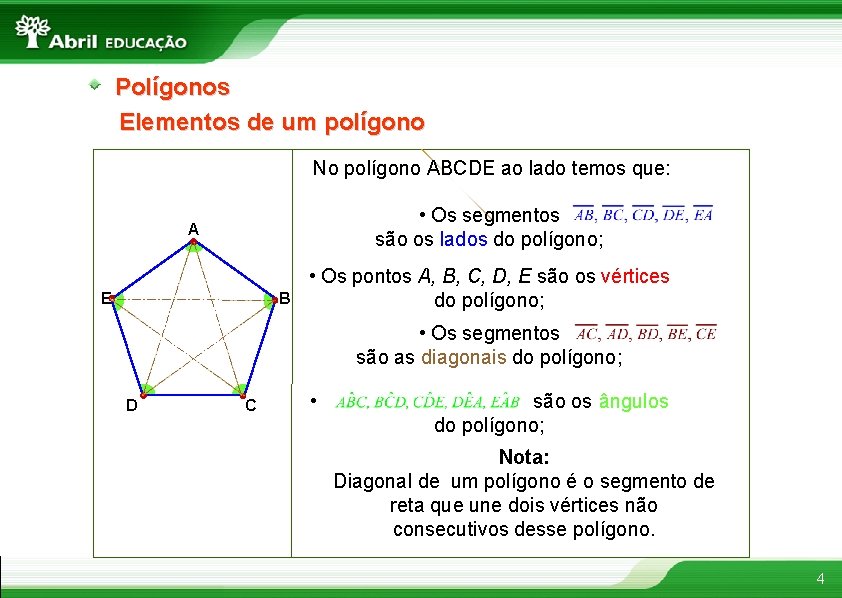
Polígonos Elementos de um polígono No polígono ABCDE ao lado temos que: • Os segmentos são os lados do polígono; A E B • Os pontos A, B, C, D, E são os vértices do polígono; • Os segmentos são as diagonais do polígono; D C • são os ângulos do polígono; Nota: Diagonal de um polígono é o segmento de reta que une dois vértices não consecutivos desse polígono. 4

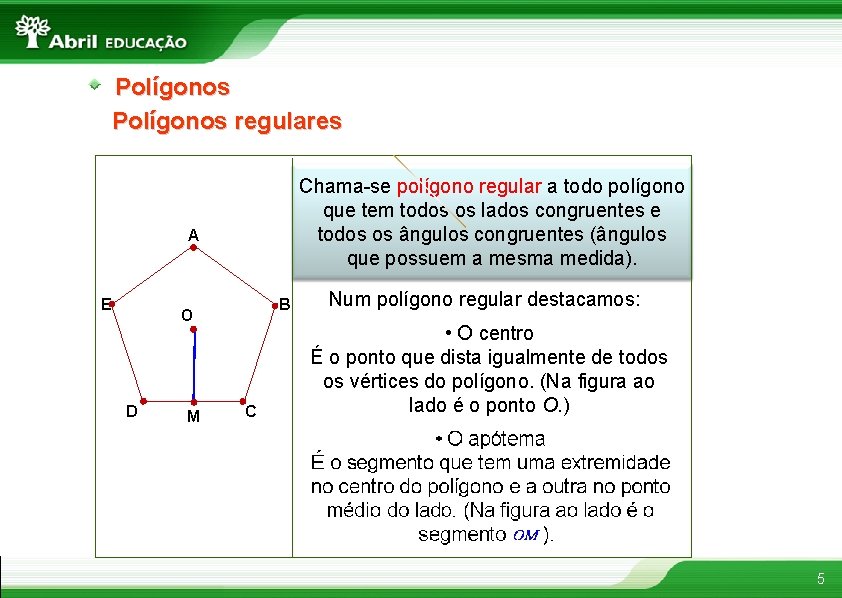
Polígonos regulares Chama-se polígono regular a todo polígono que tem todos os lados congruentes e todos os ângulos congruentes (ângulos que possuem a mesma medida). A E B O D M C Num polígono regular destacamos: • O centro É o ponto que dista igualmente de todos os vértices do polígono. (Na figura ao lado é o ponto O. ) 5

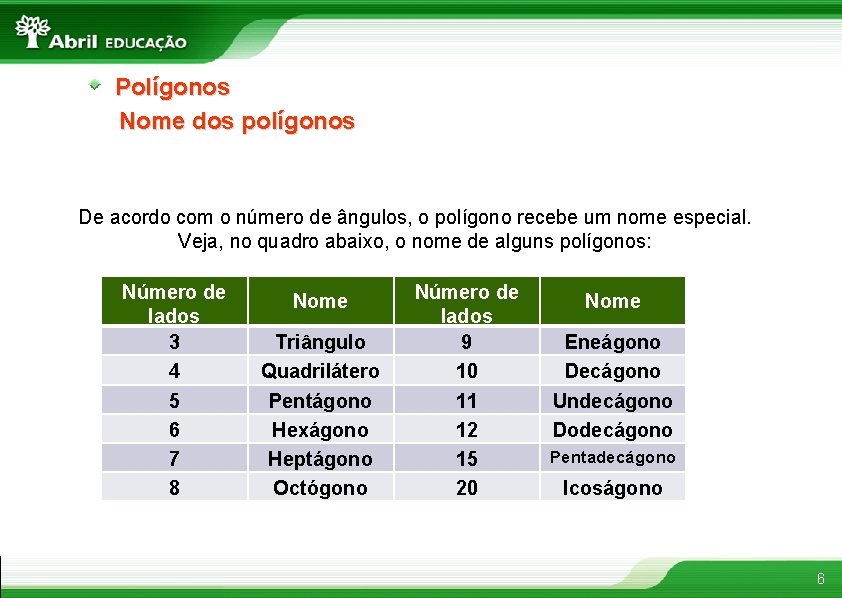
Polígonos Nome dos polígonos De acordo com o número de ângulos, o polígono recebe um nome especial. Veja, no quadro abaixo, o nome de alguns polígonos: Número de lados 3 4 5 6 7 8 Nome Triângulo Quadrilátero Pentágono Hexágono Heptágono Octógono Número de lados 9 10 11 12 15 20 Nome Eneágono Decágono Undecágono Dodecágono Pentadecágono Icoságono 6

Polígonos Soma das medidas dos ângulos internos: Soma das medidas dos ângulos externos: ngulos internos de um polígono regular: ngulos externos de um polígono regular: Número de diagonais de um polígono: 7

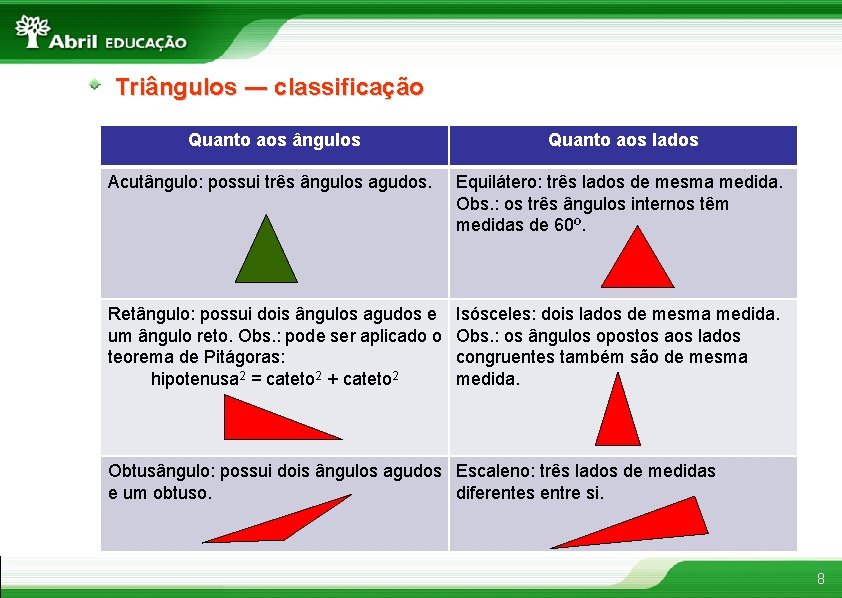
Triângulos ― classificação Quanto aos ângulos Quanto aos lados Acutângulo: possui três ângulos agudos. Equilátero: três lados de mesma medida. Obs. : os três ângulos internos têm medidas de 60º. Retângulo: possui dois ângulos agudos e um ângulo reto. Obs. : pode ser aplicado o teorema de Pitágoras: hipotenusa 2 = cateto 2 + cateto 2 Isósceles: dois lados de mesma medida. Obs. : os ângulos opostos aos lados congruentes também são de mesma medida. Obtusângulo: possui dois ângulos agudos Escaleno: três lados de medidas e um obtuso. diferentes entre si. 8

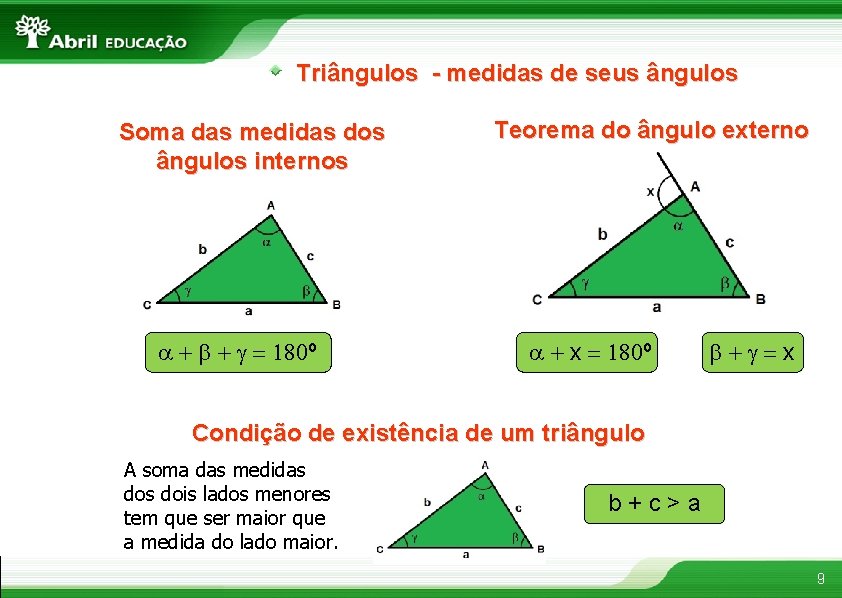
Triângulos - medidas de seus ângulos Soma das medidas dos ângulos internos a + b + g = 180º Teorema do ângulo externo a + x = 180º b+g=x Condição de existência de um triângulo A soma das medidas dois lados menores tem que ser maior que a medida do lado maior. b+c>a 9

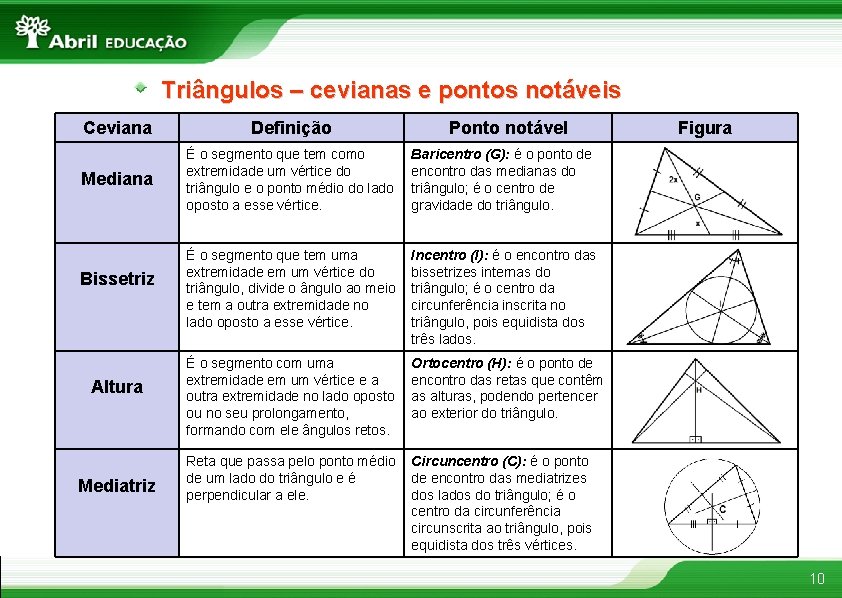
Triângulos – cevianas e pontos notáveis Ceviana Definição Mediana É o segmento que tem como extremidade um vértice do triângulo e o ponto médio do lado oposto a esse vértice. Baricentro (G): é o ponto de encontro das medianas do triângulo; é o centro de gravidade do triângulo. É o segmento que tem uma extremidade em um vértice do triângulo, divide o ângulo ao meio e tem a outra extremidade no lado oposto a esse vértice. Incentro (I): é o encontro das bissetrizes internas do triângulo; é o centro da circunferência inscrita no triângulo, pois equidista dos três lados. É o segmento com uma extremidade em um vértice e a outra extremidade no lado oposto ou no seu prolongamento, formando com ele ângulos retos. Ortocentro (H): é o ponto de encontro das retas que contêm as alturas, podendo pertencer ao exterior do triângulo. Reta que passa pelo ponto médio de um lado do triângulo e é perpendicular a ele. Circuncentro (C): é o ponto de encontro das mediatrizes dos lados do triângulo; é o centro da circunferência circunscrita ao triângulo, pois equidista dos três vértices. Bissetriz Altura Mediatriz Ponto notável Figura 10

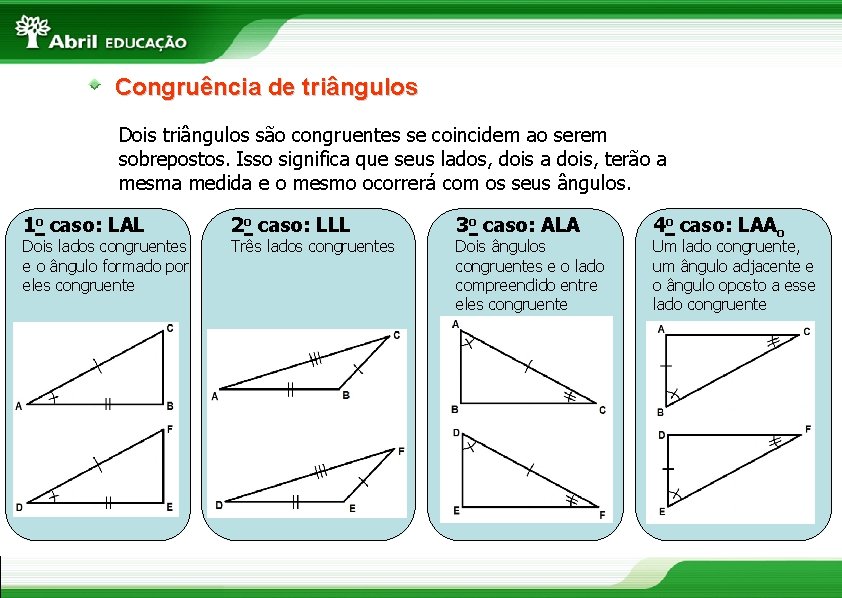
Congruência de triângulos Dois triângulos são congruentes se coincidem ao serem sobrepostos. Isso significa que seus lados, dois a dois, terão a mesma medida e o mesmo ocorrerá com os seus ângulos. 1 o caso: LAL Dois lados congruentes e o ângulo formado por eles congruente 2 o caso: LLL Três lados congruentes 3 o caso: ALA Dois ângulos congruentes e o lado compreendido entre eles congruente 4 o caso: LAAo Um lado congruente, um ângulo adjacente e o ângulo oposto a esse lado congruente 11

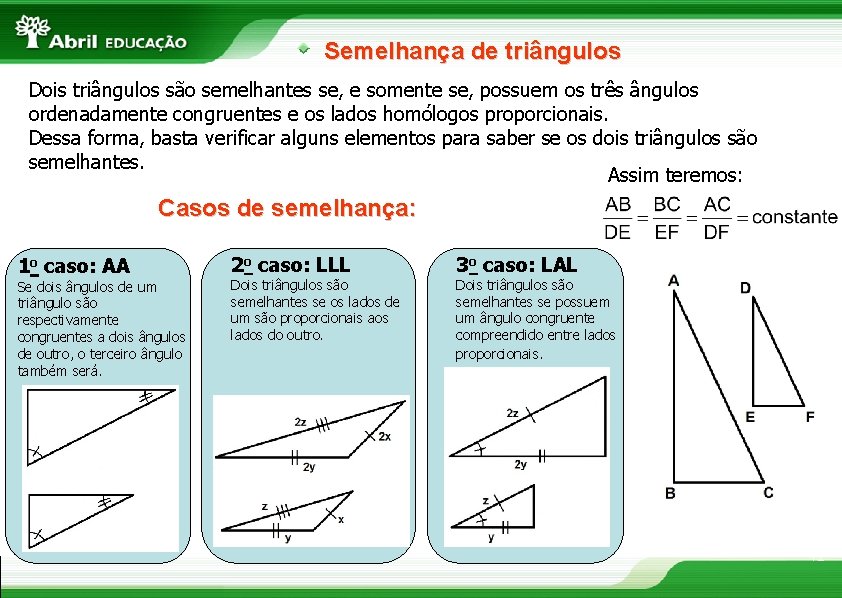
Semelhança de triângulos Dois triângulos são semelhantes se, e somente se, possuem os três ângulos ordenadamente congruentes e os lados homólogos proporcionais. Dessa forma, basta verificar alguns elementos para saber se os dois triângulos são semelhantes. Assim teremos: Casos de semelhança: 1 o caso: AA Se dois ângulos de um triângulo são respectivamente congruentes a dois ângulos de outro, o terceiro ângulo também será. 2 o caso: LLL Dois triângulos são semelhantes se os lados de um são proporcionais aos lados do outro. 3 o caso: LAL Dois triângulos são semelhantes se possuem um ângulo congruente compreendido entre lados proporcionais. 12

Relações métricas no triângulo retângulo Considere um triângulo ABC, retângulo em A, e o segmento perpendicular ao lado , com D em. Definições dos segmentos: Assim teremos: 13

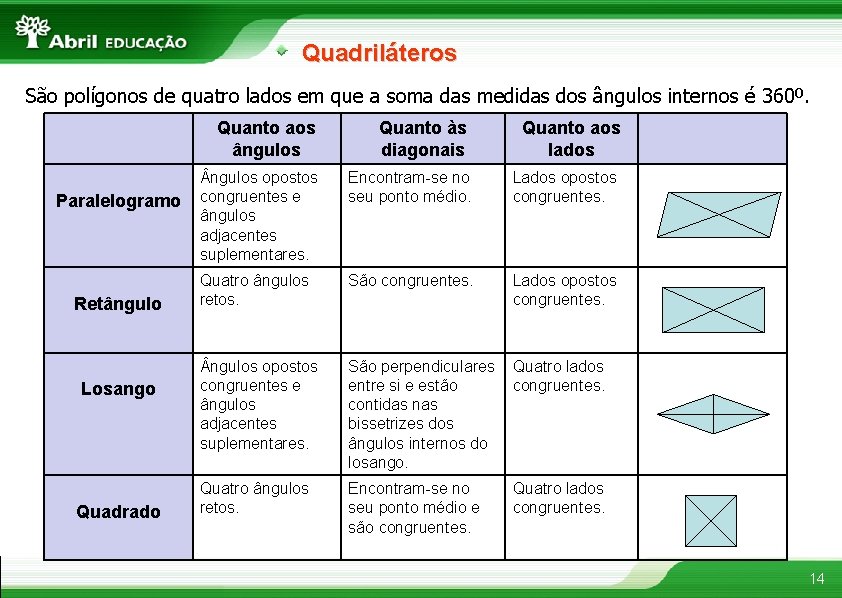
Quadriláteros São polígonos de quatro lados em que a soma das medidas dos ângulos internos é 360º. Paralelogramo Retângulo Losango Quadrado Quanto aos ângulos Quanto às diagonais Quanto aos lados ngulos opostos congruentes e ângulos adjacentes suplementares. Encontram-se no seu ponto médio. Lados opostos congruentes. Quatro ângulos retos. São congruentes. Lados opostos congruentes. ngulos opostos congruentes e ângulos adjacentes suplementares. São perpendiculares entre si e estão contidas nas bissetrizes dos ângulos internos do losango. Quatro lados congruentes. Quatro ângulos retos. Encontram-se no seu ponto médio e são congruentes. Quatro lados congruentes. 14

Quadriláteros Os trapézios são quadriláteros que têm apenas um par de lados paralelos, chamados base maior e base menor. Trapézio retângulo É todo trapézio que tem dois ângulos retos. Nele, um dos lados que não é base é perpendicular às duas bases. Trapézio isósceles É todo trapézio que tem dois lados não paralelos congruentes. 15

Teorema de Tales Um feixe de retas paralelas cortadas por duas transversais quaisquer determinam segmentos proporcionais. Assim teremos: 16

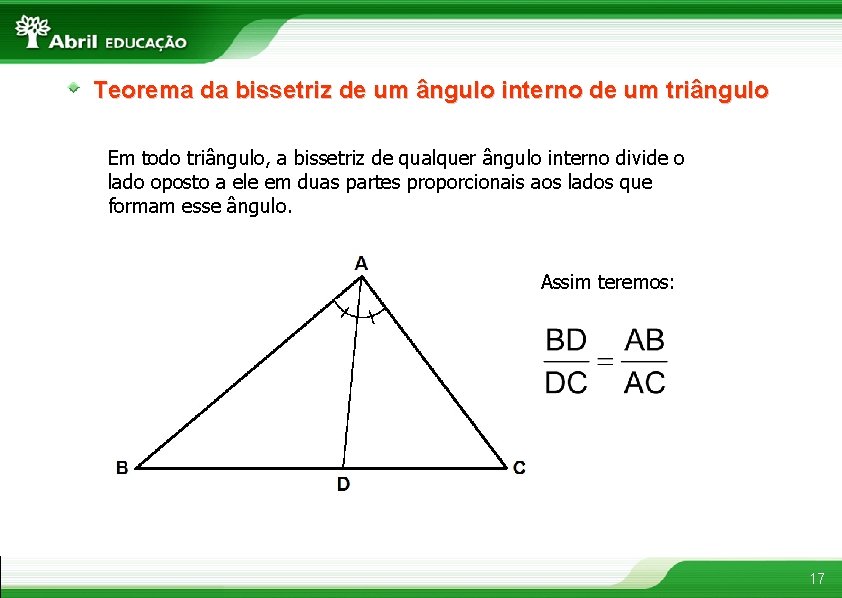
Teorema da bissetriz de um ângulo interno de um triângulo Em todo triângulo, a bissetriz de qualquer ângulo interno divide o lado oposto a ele em duas partes proporcionais aos lados que formam esse ângulo. Assim teremos: 17