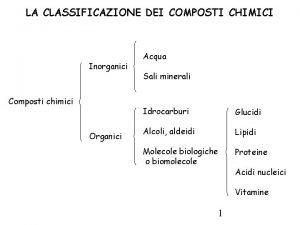
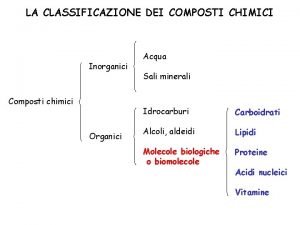
Prof Amelia Vavalli 24 03 2008 Classificazione dei












- Slides: 35

Prof. Amelia Vavalli 24. 03. 2008

Classificazione dei quadrilateri Proprietà Rettangolo Quadrato Rombo Parallelogramma Trapezio


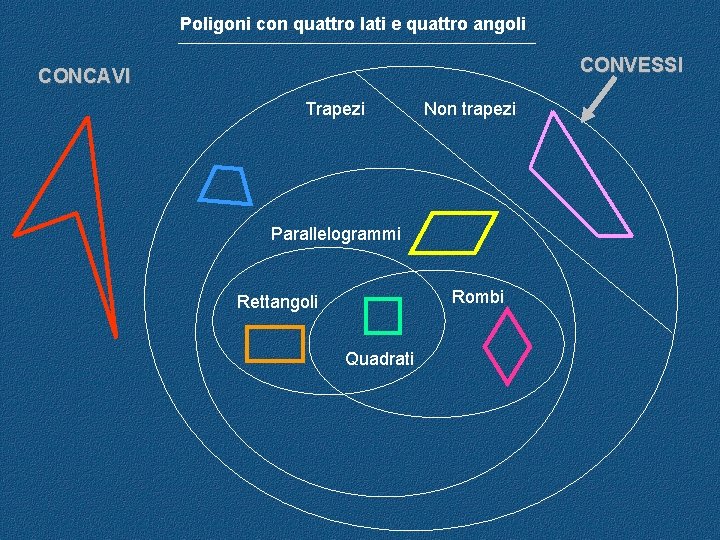
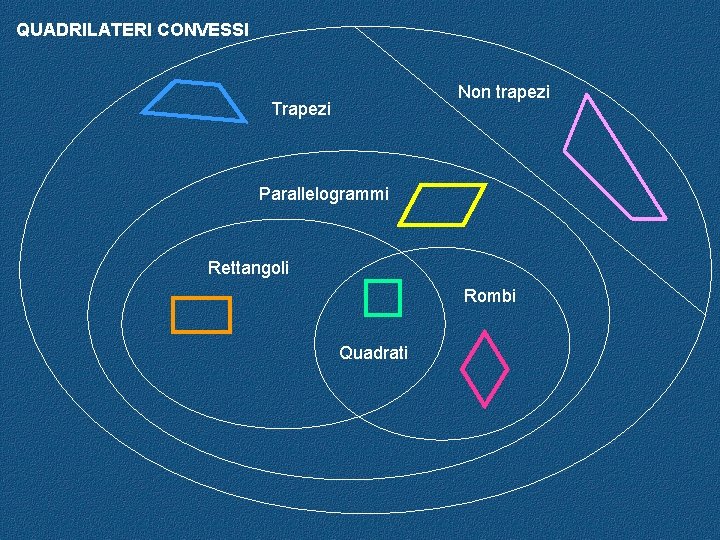
Poligoni con quattro lati e quattro angoli CONVESSI CONCAVI Trapezi Non trapezi Parallelogrammi Rombi Rettangoli Quadrati

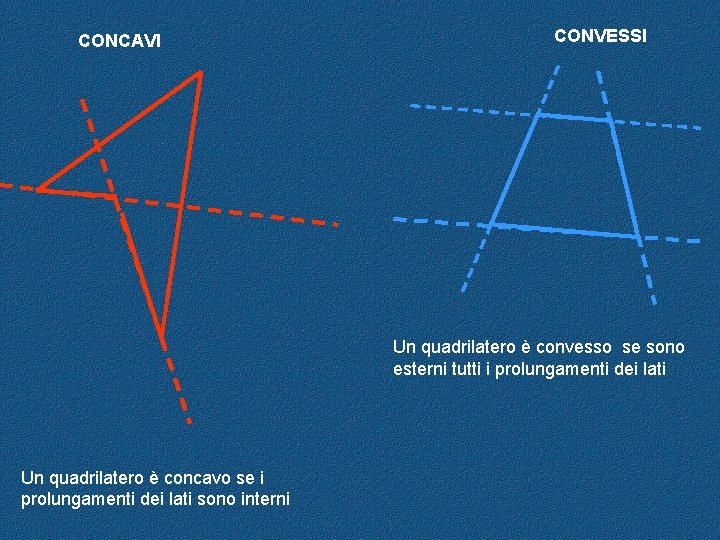
CONCAVI CONVESSI Un quadrilatero è convesso se sono esterni tutti i prolungamenti dei lati Un quadrilatero è concavo se i prolungamenti dei lati sono interni


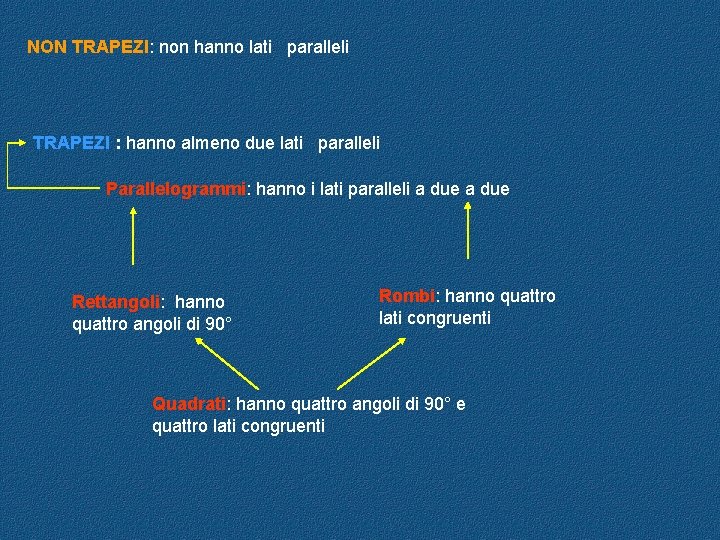
NON TRAPEZI: non hanno lati paralleli TRAPEZI : hanno almeno due lati paralleli Parallelogrammi: hanno i lati paralleli a due Rettangoli: hanno quattro angoli di 90° Rombi: hanno quattro lati congruenti Quadrati: hanno quattro angoli di 90° e quattro lati congruenti

QUADRILATERI CONVESSI Non trapezi Trapezi Parallelogrammi Rettangoli Rombi Quadrati


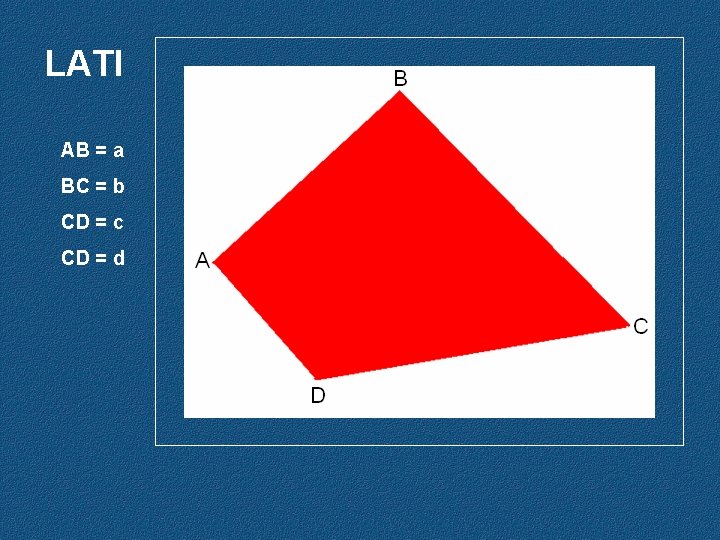
LATI AB = a BC = b CD = c CD = d

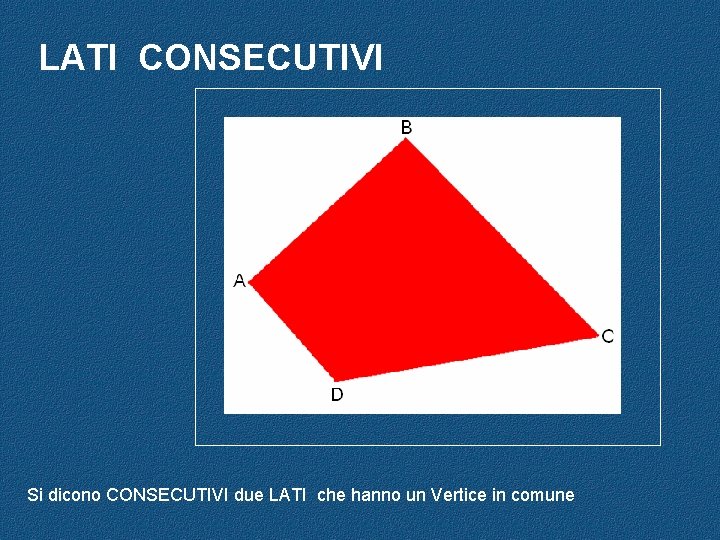
LATI CONSECUTIVI Si dicono CONSECUTIVI due LATI che hanno un Vertice in comune

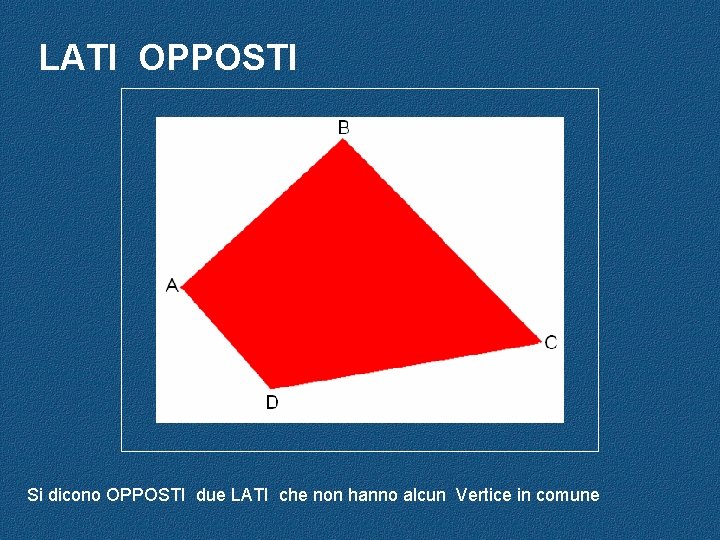
LATI OPPOSTI Si dicono OPPOSTI due LATI che non hanno alcun Vertice in comune

VERTICI A B C D Sono i punti di incontro di due lati consecutivi

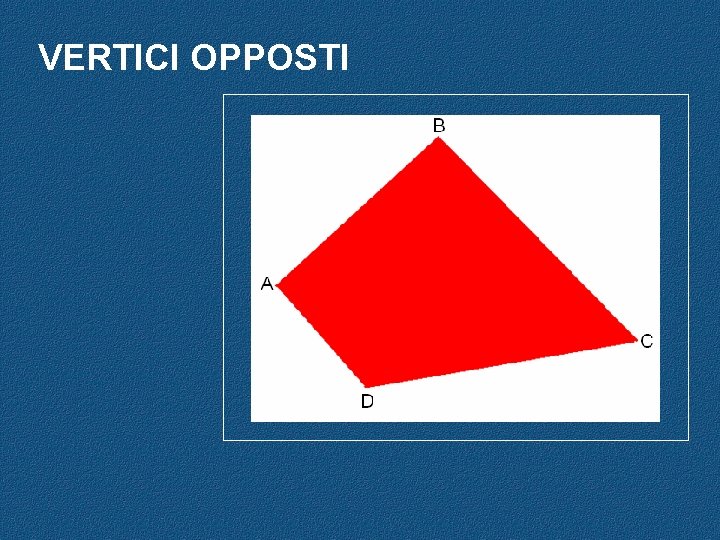
VERTICI OPPOSTI

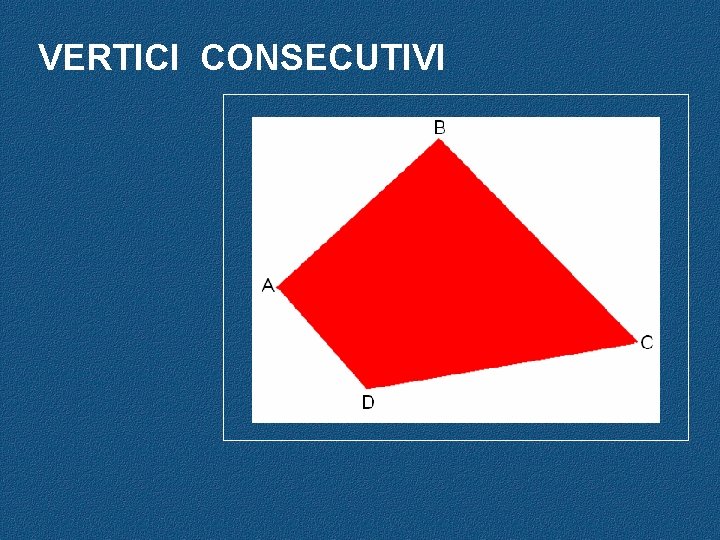
VERTICI CONSECUTIVI

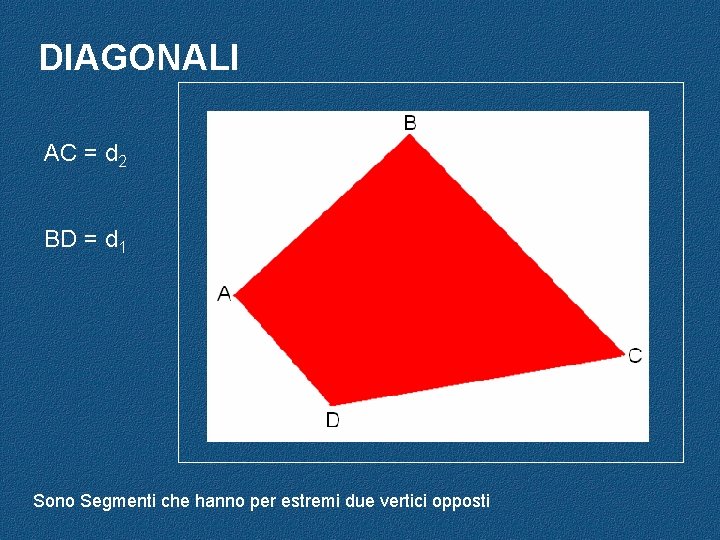
DIAGONALI AC = d 2 BD = d 1 Sono Segmenti che hanno per estremi due vertici opposti

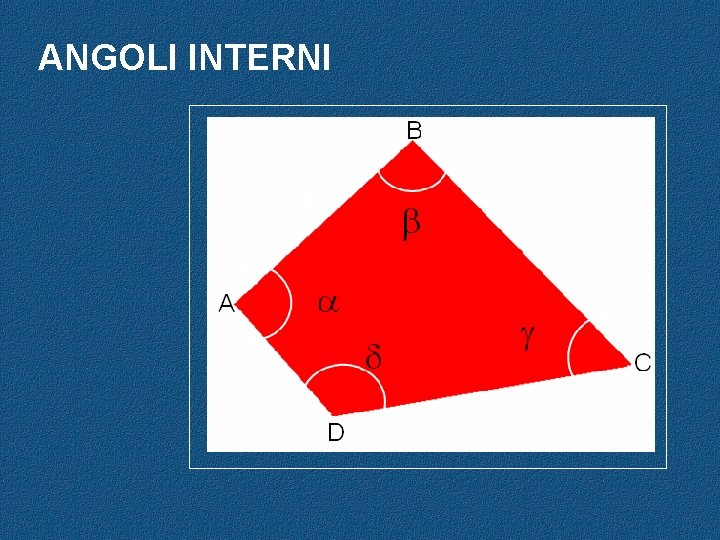
ANGOLI INTERNI

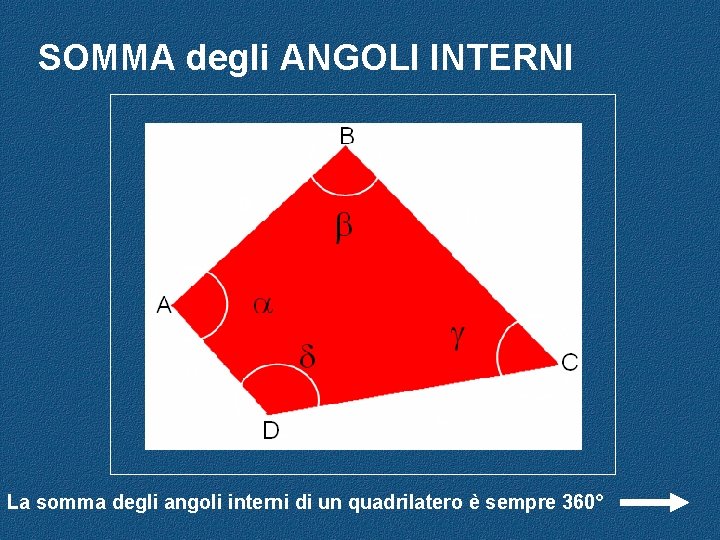
SOMMA degli ANGOLI INTERNI La somma degli angoli interni di un quadrilatero è sempre 360°

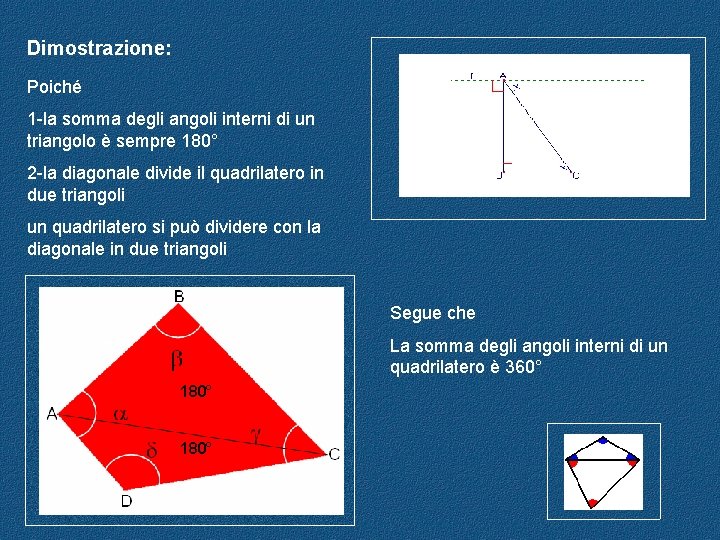
Dimostrazione: Poiché 1 -la somma degli angoli interni di un triangolo è sempre 180° 2 -la diagonale divide il quadrilatero in due triangoli un quadrilatero si può dividere con la diagonale in due triangoli Segue che La somma degli angoli interni di un quadrilatero è 360° 180°


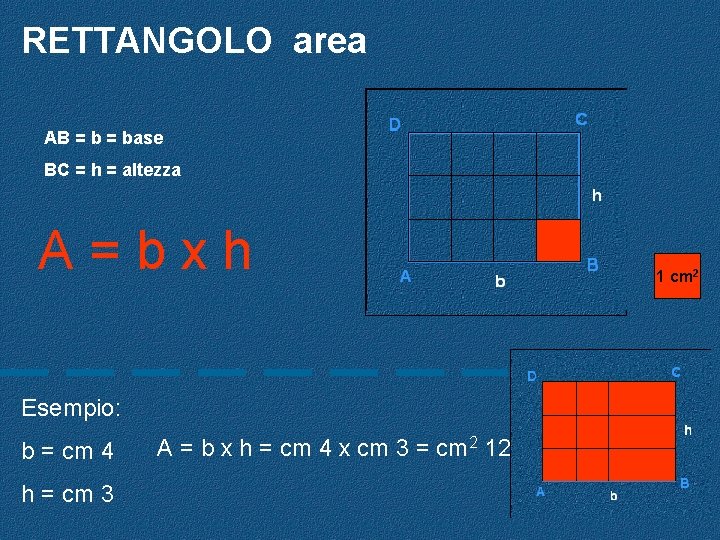
RETTANGOLO area AB = base BC = h = altezza A=bxh Esempio: b = cm 4 h = cm 3 A = b x h = cm 4 x cm 3 = cm 2 12 1 cm 2

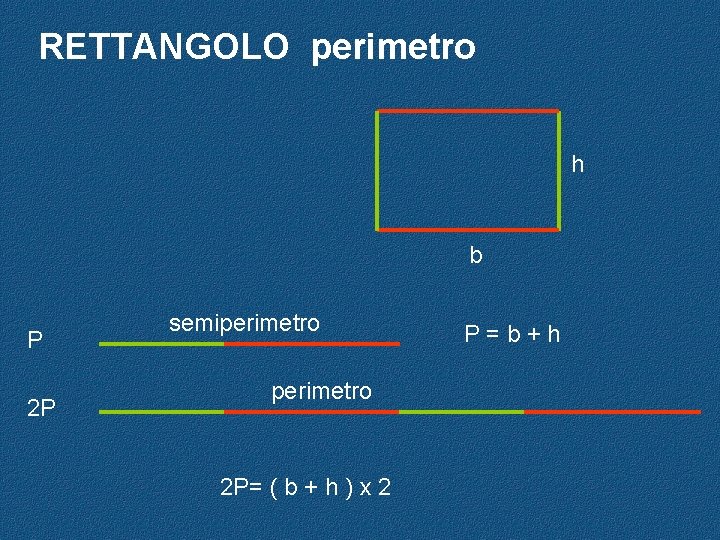
RETTANGOLO perimetro h b P 2 P semiperimetro 2 P= ( b + h ) x 2 P=b+h


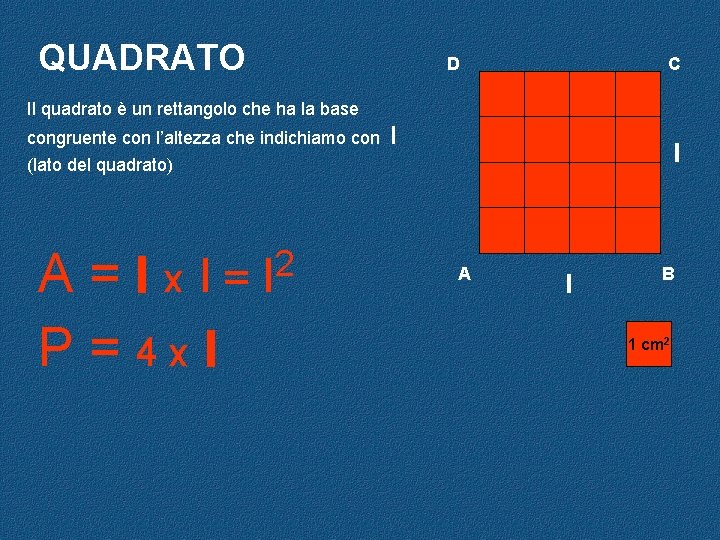
QUADRATO D C Il quadrato è un rettangolo che ha la base congruente con l’altezza che indichiamo con (lato del quadrato) A = l x l= P = 4 x l 2 l l l A l B 1 cm 2


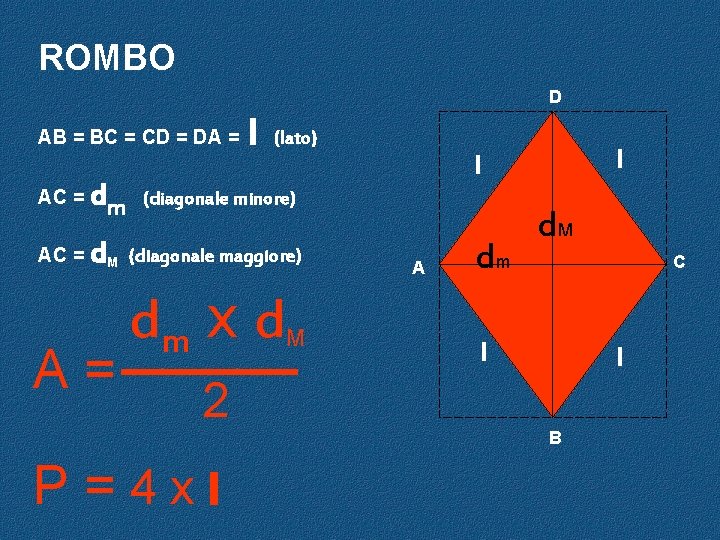
ROMBO D AB = BC = CD = DA = l (lato) AC = dm (diagonale minore) AC = d. M (diagonale maggiore) A= dm x d l l M A dm d. M C l l 2 B P=4 xl

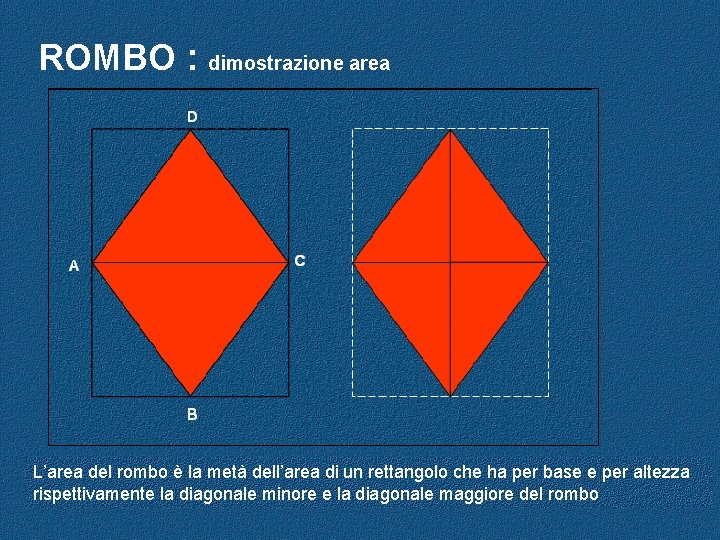
ROMBO : dimostrazione area L’area del rombo è la metà dell’area di un rettangolo che ha per base e per altezza rispettivamente la diagonale minore e la diagonale maggiore del rombo


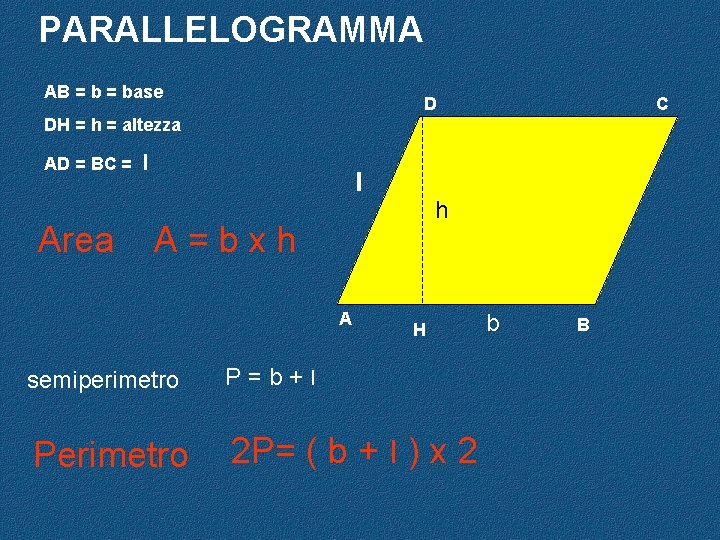
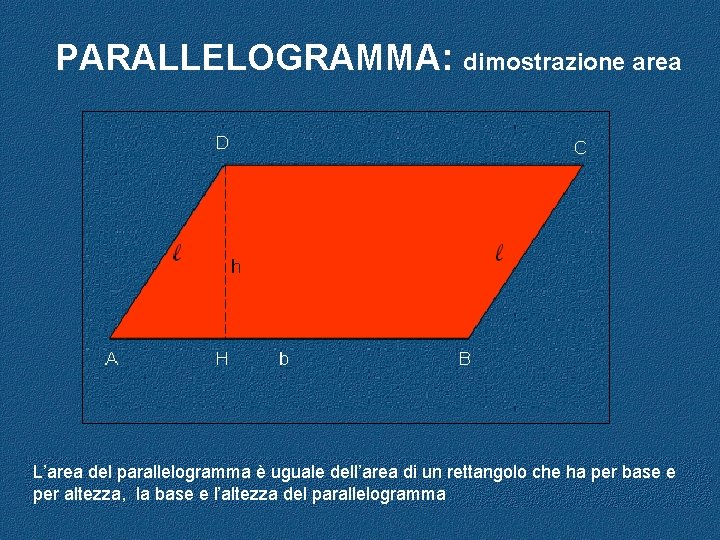
PARALLELOGRAMMA AB = base D C DH = h = altezza AD = BC = Area l l h A=bxh A H semiperimetro P=b+l Perimetro 2 P= ( b + l ) x 2 b B

PARALLELOGRAMMA: dimostrazione area L’area del parallelogramma è uguale dell’area di un rettangolo che ha per base e per altezza, la base e l’altezza del parallelogramma


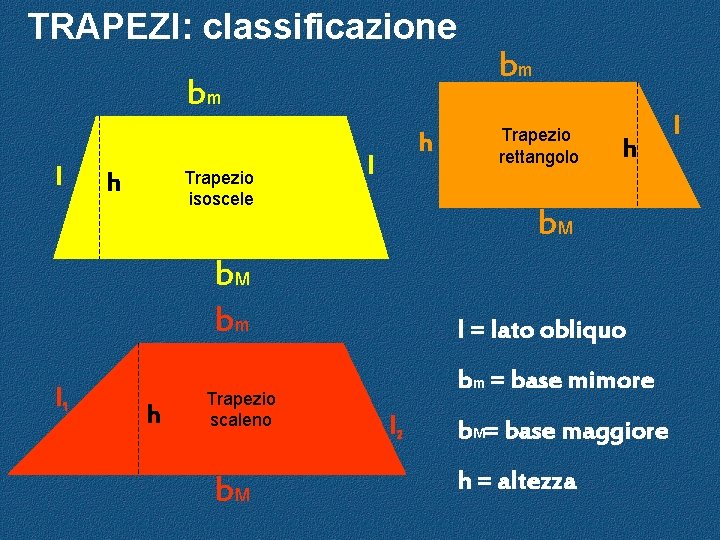
TRAPEZI: classificazione bm l Trapezio isoscele h h l h Trapezio scaleno b. M Trapezio rettangolo h b. M bm l 1 bm l = lato obliquo bm = base mimore l 2 b. M= base maggiore h = altezza l

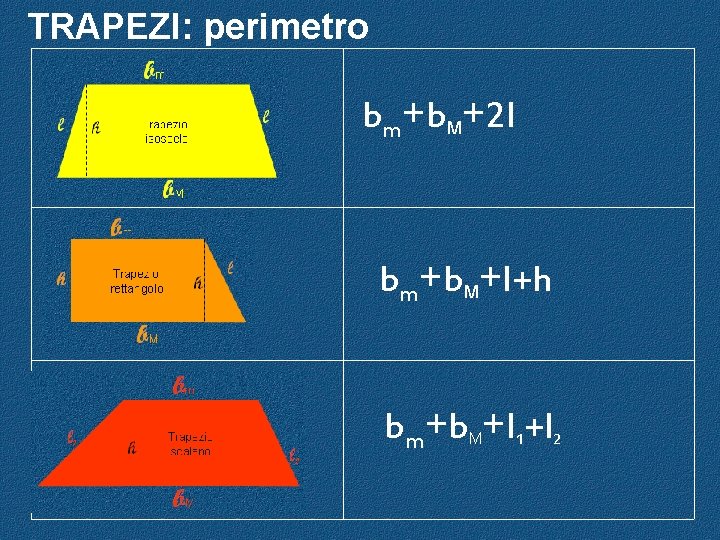
TRAPEZI: perimetro bm+b. M+2 l bm+b. M+l+h bm+b +l +l M 1 2

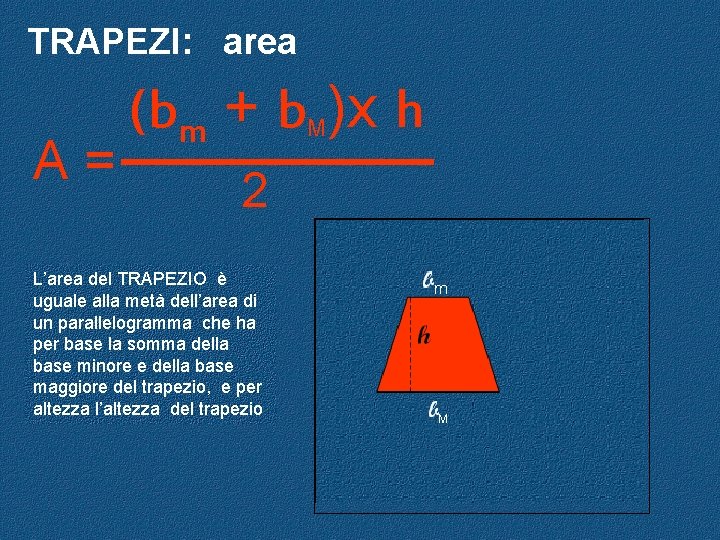
TRAPEZI: area A= (bm + b )x h M 2 L’area del TRAPEZIO è uguale alla metà dell’area di un parallelogramma che ha per base la somma della base minore e della base maggiore del trapezio, e per altezza l’altezza del trapezio

Prof. Amelia Vavalli
 2008 2008
2008 2008 Classificazione nazionale dei dispositivi medici
Classificazione nazionale dei dispositivi medici Mappa nomenclatura chimica
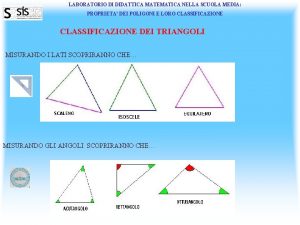
Mappa nomenclatura chimica Classificazione dei triangoli rispetto agli angoli
Classificazione dei triangoli rispetto agli angoli Classificazione dei metalli
Classificazione dei metalli Classificazione vegetale
Classificazione vegetale Classificazione dei segnali
Classificazione dei segnali Classificazione dei quadrilateri
Classificazione dei quadrilateri Classificazione e proprietà dei materiali
Classificazione e proprietà dei materiali Classificazione dei gas
Classificazione dei gas Composti binari schema
Composti binari schema Reticolo a corpo centrato
Reticolo a corpo centrato Sostanze organiche e inorganiche
Sostanze organiche e inorganiche Programmazione imperativa e dichiarativa
Programmazione imperativa e dichiarativa I cinque regni dei viventi per bambini
I cinque regni dei viventi per bambini Classificazione dei gas
Classificazione dei gas Classificazione nazionale dei dispositivi medici
Classificazione nazionale dei dispositivi medici Solfuro nichelico formula
Solfuro nichelico formula I cinque regni
I cinque regni Mappa concettuale composti binari e ternari
Mappa concettuale composti binari e ternari Classificazione carboidrati
Classificazione carboidrati Classificazione vini italiani
Classificazione vini italiani I quadrilateri scuola media
I quadrilateri scuola media Classificazione dei computer
Classificazione dei computer Mappa concettuale nomenclatura chimica
Mappa concettuale nomenclatura chimica Area del trapezio dimostrazione
Area del trapezio dimostrazione Giaguaro
Giaguaro Diagramma quadrilateri
Diagramma quadrilateri Quadrilatero concavo e convesso
Quadrilatero concavo e convesso Classificazione dei rifiuti
Classificazione dei rifiuti Mappa rocce
Mappa rocce N fissi poligoni regolari
N fissi poligoni regolari Agnus dei agnus dei qui tollis peccata peccata mundi
Agnus dei agnus dei qui tollis peccata peccata mundi Francesco rinaldi la marcia dei diritti ascolta
Francesco rinaldi la marcia dei diritti ascolta Pada unix, file dibagi menjadi 3 kategori utama
Pada unix, file dibagi menjadi 3 kategori utama What was amelia earhart's accomplishments
What was amelia earhart's accomplishments