AA209 Aerodinmica da Asa e Fuselagem em Regime

































- Slides: 49

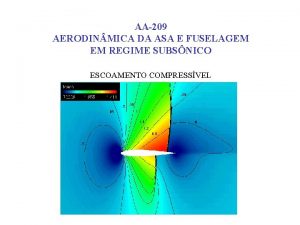
AA-209 Aerodinâmica da Asa e Fuselagem em Regime Subsônico Prof. GIL

Conceituação • Métodos de elementos discretos forma mais geral de classificar os conhecidos métodos de painéis e de malha de vórtices. • Todavia, baseiam-se no mesmo princípio, empregar singularidades aerodinâmicas cujas funções de potencial são soluções da equação de Laplace: • Elementos discretos: – São lugares geométricos elementares aos quais de associa a posição de uma singularidade ou distribuição de singularidades; – Os pontos e/ou superfícies elementares, por exemplo, são definidos de forma a discretizar um corpo em regiões elementares, transformando uma superfície continua em um conjunto de superfícies que “aproximam” a forma do corpo. 2

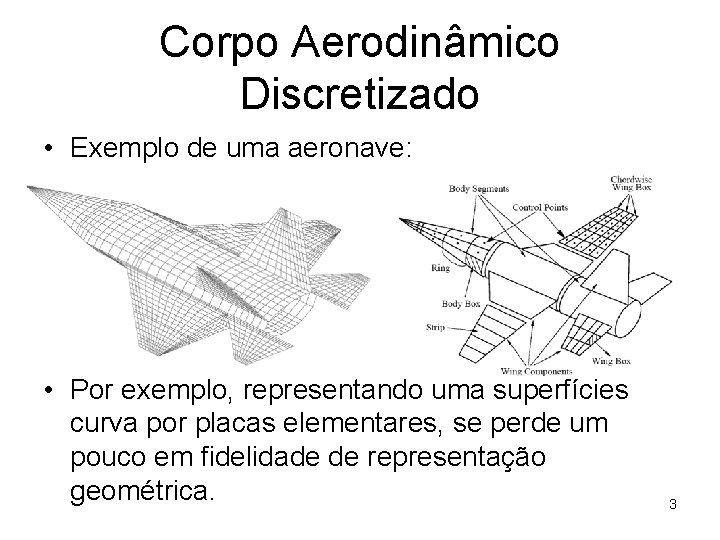
Corpo Aerodinâmico Discretizado • Exemplo de uma aeronave: • Por exemplo, representando uma superfícies curva por placas elementares, se perde um pouco em fidelidade de representação geométrica. 3

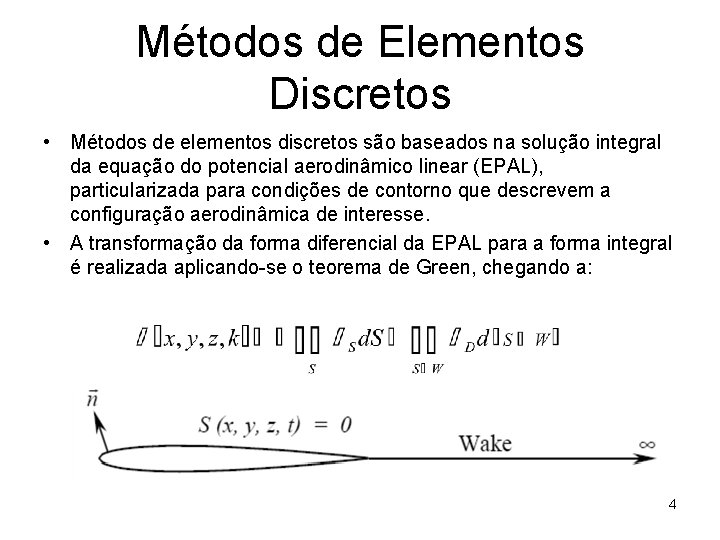
Métodos de Elementos Discretos • Métodos de elementos discretos são baseados na solução integral da equação do potencial aerodinâmico linear (EPAL), particularizada para condições de contorno que descrevem a configuração aerodinâmica de interesse. • A transformação da forma diferencial da EPAL para a forma integral é realizada aplicando-se o teorema de Green, chegando a: 4

Solução Elementar • Esta equação integral assume que sobre a superfície S, são distribuídas fontes js e dipolos jd (soluções elementares da equação do potencial aerodinâmico linear), bem como nas superfícies que definem a esteira aerodinâmica (W - Wake). • O potencial devido uma fonte e um dipolo de intensidade s e m (ou Dj ) são, por exemplo, dados por: onde, Posição da fonte Ponto que recebe Distância entre a fonte e o ponto que recebe 5

Método de Painéis de Hess-Smith • Dentre as várias formas para se formular um método de painéis, o método mais simples e prático é conhecido como Hess-Smith, desenvolvido na Douglas Aircraft Co. , em 1966. • Este método é baseado na distribuição de fontes e vórtices na superfície da geometria a ser modelada tal que: φ = φ∞ + φS + φV onde, φ é a função potencial de velocidade tal e as três parcelas correspondem ao escoamento não perturbado, distribuição de fontes e de vórtices, respectivamente. • A duas últimas componentes tem intensidades variantes de acordo com a sua posição q(s) e γ(s), onde s é uma coordenada curvilínea que envolve toda a superfícies de um aerofólio, por exemplo, da forma que for geometricamente mais conveniente. 6

Método de Painéis de Hess-Smith • Os potenciais criados pela distribuição de fontes / sumidouros e vórtices são dados por: onde as variáveis das equações acima são definidas na figura abaixo: 7

Método de Painéis de Hess-Smith • Observe que, nas relações integrais dadas, a integração deve ser realizada ao longo da superfície total do aerofólio. • Admitindo o princípio da superposição, qualquer distribuição de fontes / sumidouros e vórtices deve satisfazer a equação de Laplace, • Todavia, deve-se encontrar condições para q (s) e γ (s) de tal forma que sejam satisfeitas simultaneamente as condições de tangência do escoamento e de Kutta • Note que temos várias opções. Em teoria, poderíamos: – Assumir uma distribuição de intensidade de fontes que satisfaça a condição de tangência e uma de intensidade de vórtices que atenda a condição de Kutta; – Admitir uma combinação arbitrária de singularidades (fontes, vórtices) de forma a atender as condições de contorno de tangência e de Kutta simultaneamente. 8

Método de Painéis de Hess-Smith • Hess e Smith assumiram a seguinte simplificação que é válida: – Estabelecer que a intensidade de vórtice é constante ao longo de todo o aerofólio, empregando a condição de Kutta para fixar este valor. – Admite-se, no entanto que a distribuição de intensidade de fontes é variável de painel para painel de forma a atender a condição de tangência do escoamento sobre o corpo, ou seja em todo os painéis simultaneamente 9

Método de Painéis de Hess-Smith • Baseado na aproximação sugerida por Hess e Smith, podemos representar φ = φ∞ + φS + φV como: lembrado que: • onde a é o ângulo de ataque o escoamento não perturbado faz com o corpo. Note que integração no corpo passa a ser representada por uma somatória, e que a vorticidade γ independe da geometria, isto é deve ser 10 constante para todos os painéis

Método de Painéis de Hess-Smith • Portanto, temos N + 1 incógnitas para resolver no nosso problema: os N painéis fonte qi mais a intensidade de vórtice γ a se determinar. ( o que implica em N + 1 incógnitas) • Conseqüentemente, serão necessárias N + 1 equações independentes, a partir da condição de tangência do fluxo em cada (N) painel, bem como a condição de Kutta (N+1) que garante a existência da vorticidade (circulação). • A solução do problema portanto exigirá a inversão de uma matriz de dimensão (N +1) × (N +1). • Condição de contorno: onde devemos impor a condição de escoamento tangente? As opções disponíveis são: – Os nós resultantes do processo de “panelização”; – Ou ponto sobre a superfície real ao invés do painel; – Ponto no meio do painel. 11

Condição de Kutta • Condição de tangência ou: para i=1, N. • Condição de Kutta: onde os sinais opostos deve-se ao fato que os vetores tangenciais no primeiro (1) e último (N) painel tem sinais opostos. • As velocidades nos pontos médios de cada painel pode ser obtida através da superposição das contribuições (interferências) de todas as fontes e vórtices arranjados sobre cada painel incluindo a influência do painel nele mesmo. • Uma vez que a velocidade induzida é proporcional a intensidade das singularidades dispostas sobre este painéis qi e γ, pode-se tirar da relação integral a seguir: 12

Condições de Tangência e de Kutta • Na realidade chegou-se a um sistema matricial, que relaciona as intensidade de vórtices e fontes às condições de contorno • As equações algébricas são desta forma relacionadas ao vetor: que na realidade representa apenas as condição de tangência do escoamento. Com temos na realidade um sistema de N+1 equações, deve-se empregara a condição de Kutta como condição complementar e assim termo um sistema determinado. resultando em: onde a condição de Kutta é dada por. 13

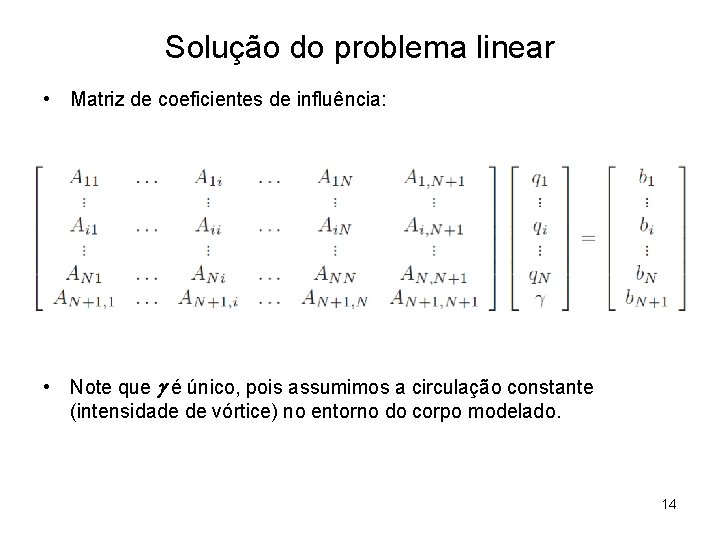
Solução do problema linear • Matriz de coeficientes de influência: • Note que g é único, pois assumimos a circulação constante (intensidade de vórtice) no entorno do corpo modelado. 14

Resultados desejados • Com o vetor de velocidade tangencias obtidos de: • Pode-se obter os coeficientes de pressão e por sua vez os esforços distribuídos sobre o corpo: • Assumindo que a coeficiente de pressão é constante sobre cada painel. 15

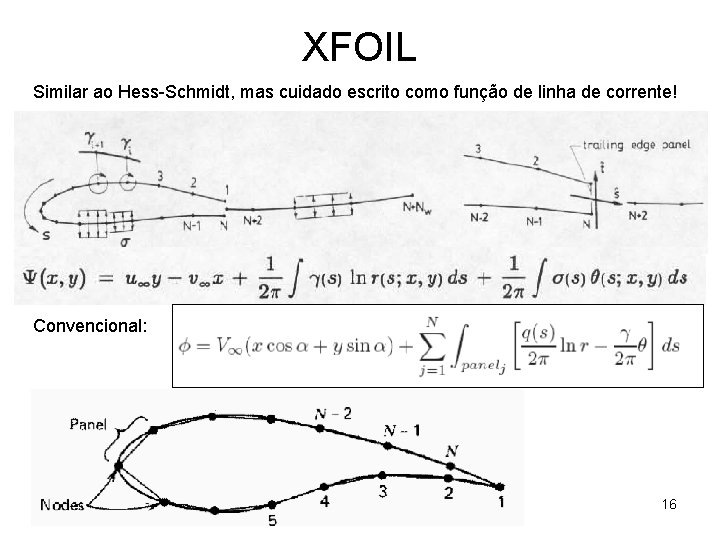
XFOIL Similar ao Hess-Schmidt, mas cuidado escrito como função de linha de corrente! Convencional: 16

O Método Vortex Lattice

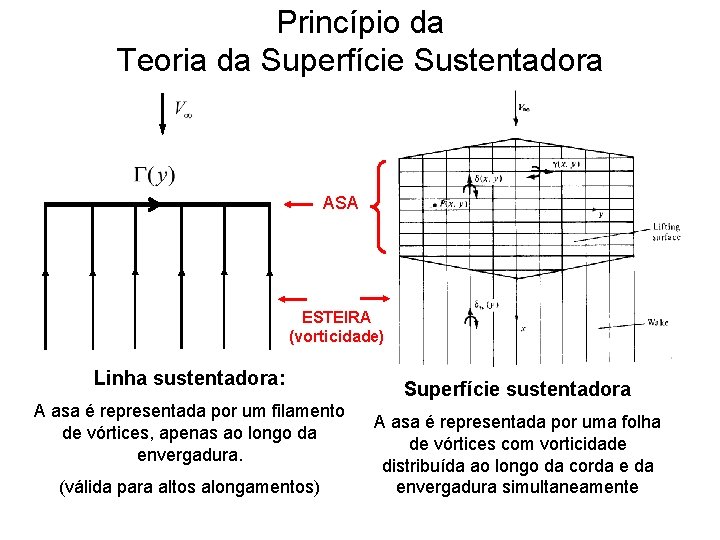
Princípio da Teoria da Superfície Sustentadora ASA ESTEIRA (vorticidade) Linha sustentadora: A asa é representada por um filamento de vórtices, apenas ao longo da envergadura. (válida para altos alongamentos) Superfície sustentadora A asa é representada por uma folha de vórtices com vorticidade distribuída ao longo da corda envergadura simultaneamente

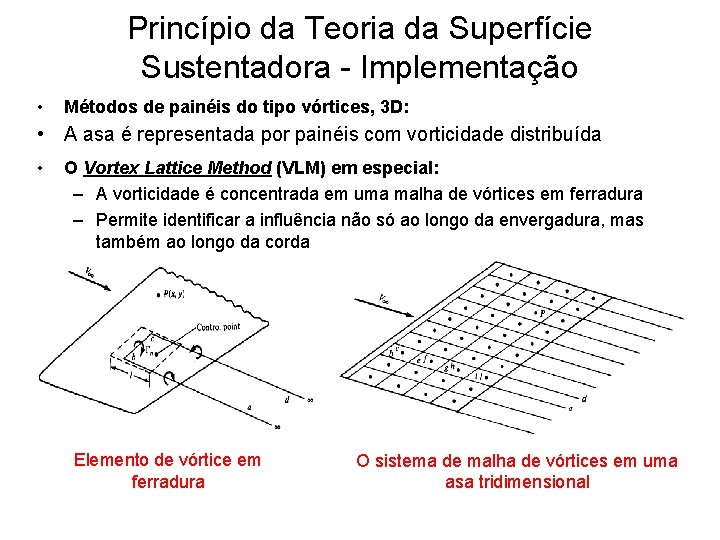
Princípio da Teoria da Superfície Sustentadora - Implementação • Métodos de painéis do tipo vórtices, 3 D: • A asa é representada por painéis com vorticidade distribuída • O Vortex Lattice Method (VLM) em especial: – A vorticidade é concentrada em uma malha de vórtices em ferradura – Permite identificar a influência não só ao longo da envergadura, mas também ao longo da corda Elemento de vórtice em ferradura O sistema de malha de vórtices em uma asa tridimensional




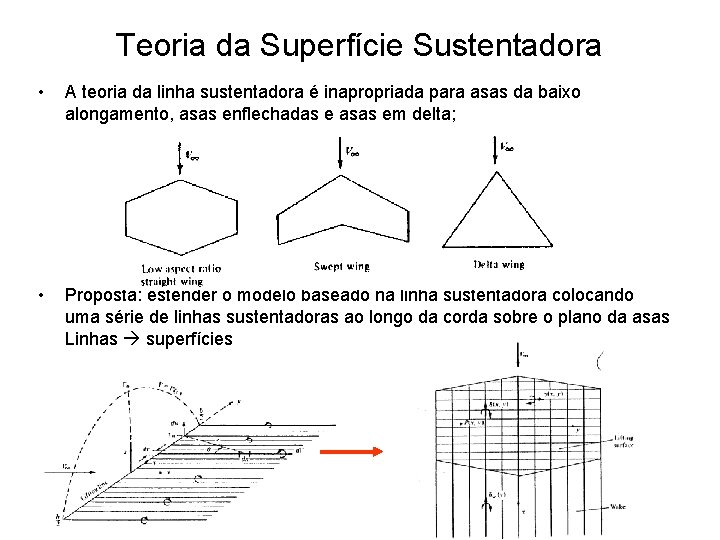
Teoria da Superfície Sustentadora • A teoria da linha sustentadora é inapropriada para asas da baixo alongamento, asas enflechadas e asas em delta; • Proposta: estender o modelo baseado na linha sustentadora colocando uma série de linhas sustentadoras ao longo da corda sobre o plano da asas Linhas superfícies

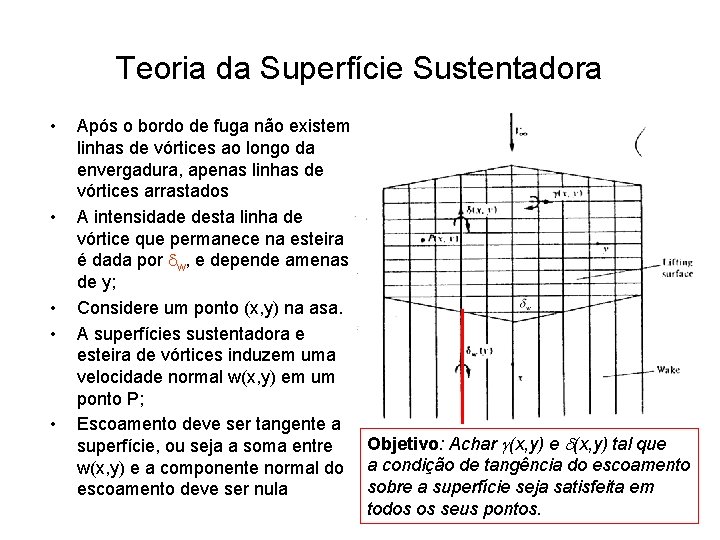
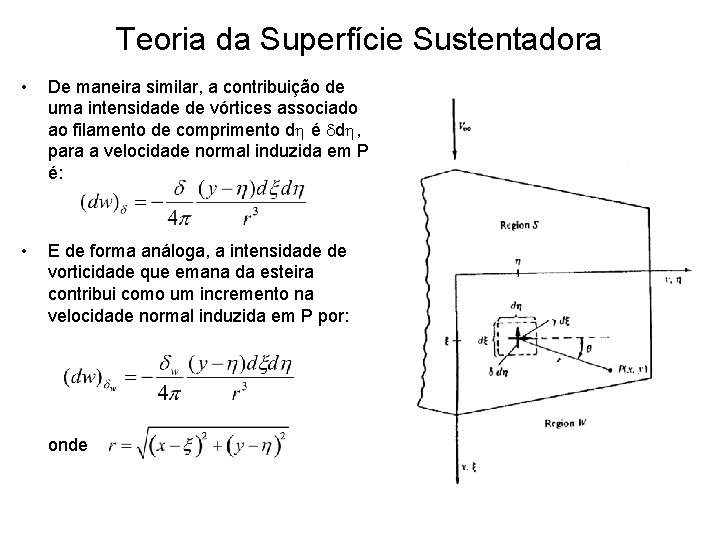
Teoria da Superfície Sustentadora • • • Após o bordo de fuga não existem linhas de vórtices ao longo da envergadura, apenas linhas de vórtices arrastados A intensidade desta linha de vórtice que permanece na esteira é dada por dw, e depende amenas de y; Considere um ponto (x, y) na asa. A superfícies sustentadora e esteira de vórtices induzem uma velocidade normal w(x, y) em um ponto P; Escoamento deve ser tangente a Objetivo: Achar g(x, y) e d(x, y) tal que superfície, ou seja a soma entre w(x, y) e a componente normal do a condição de tangência do escoamento sobre a superfície seja satisfeita em escoamento deve ser nula todos os seus pontos.

Teoria da Superfície Sustentadora • • • Expressão para a velocidade norma induzida w(x, y)em termos de g, d e dw Considere um ponto do pelas coordenadas (x, h); Intensidade do vórtice ligado g(x, h) A intensidade do filamento de vórtice arrastado de comprimento dx será gdx Da lei de Biot-Savart a velocidade incremental induzida em P devido a um seguimento vorticidade de comprimento dh dh alinhado com a envergadura, com intensidade gdx é dado por: (5. 78)

Teoria da Superfície Sustentadora • De maneira similar, a contribuição de uma intensidade de vórtices associado ao filamento de comprimento dh é ddh, para a velocidade normal induzida em P é: • E de forma análoga, a intensidade de vorticidade que emana da esteira contribui como um incremento na velocidade normal induzida em P por: onde

Teoria da Superfície Sustentadora • Para se obter a influência da distribuição de vorticidade devido a cada parte dos vórtices em ferradura, sendo elas as arrastadas e a ligada, deve-se integrar (somar) tais contribuições desta vorticidade distribuída ao longo de toda a superfícies para se obter uma velocidade normal induzida no ponto P tomando o cuidado de integrar separadamente a contribuição devido a esteira (região W), dada pela relação: Resultando em:

Teoria da Superfície Sustentadora • • A dificuldade está na solução da equação da teoria da superfícies sustentadora para g(x, y) e d(x, y), Solução numérica : Dividir a asa (superfície sustentadora) em um numero finito de painéis; A cada painel associa-se um ponto de controle onde se mede a velocidade normal induzida; Relaciona-se as velocidade normais induzidas a uma condição de contorno: w(x, y) e componente normal da velocidade de escoamento não perturbado que ser iguais. Ou seja, para atender a condição de escoamento tangente, w(x, y)=Usena, por exemplo, onde U é a velocidade e a um ângulo de ataque; Resultado: em um sistema se equações algébricas relacionando as condições de contorno em cada ponto de controle para se obter as intensidade de vorticidade g(x, y) e d(x, y) Exemplo – Método da Malha de Vórtices – (Vortex Lattice Method)

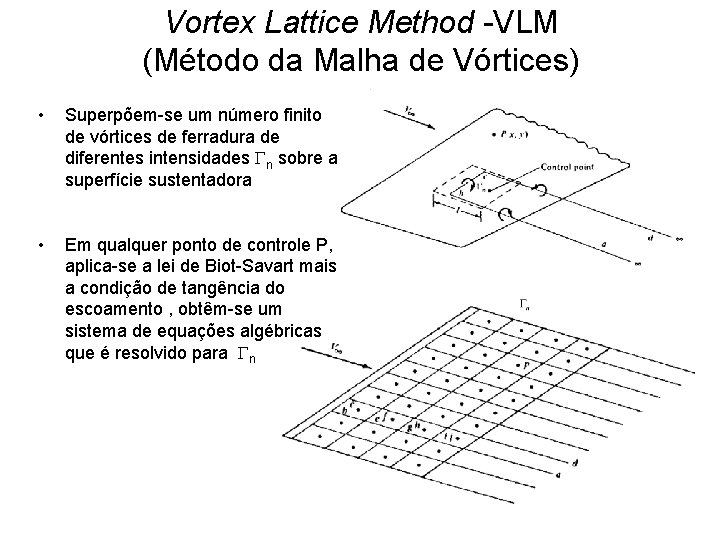
Vortex Lattice Method -VLM (Método da Malha de Vórtices) • Superpõem-se um número finito de vórtices de ferradura de diferentes intensidades Gn sobre a superfície sustentadora • Em qualquer ponto de controle P, aplica-se a lei de Biot-Savart mais a condição de tangência do escoamento , obtêm-se um sistema de equações algébricas que é resolvido para Gn

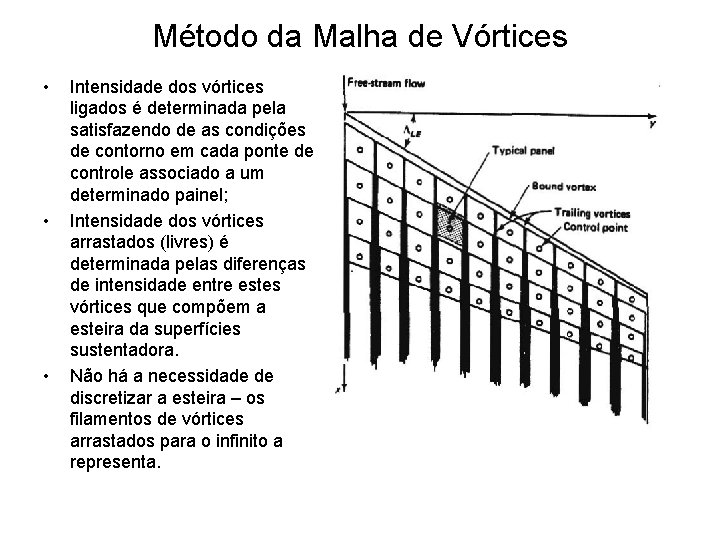
Método da Malha de Vórtices • • • Intensidade dos vórtices ligados é determinada pela satisfazendo de as condições de contorno em cada ponte de controle associado a um determinado painel; Intensidade dos vórtices arrastados (livres) é determinada pelas diferenças de intensidade entre estes vórtices que compõem a esteira da superfícies sustentadora. Não há a necessidade de discretizar a esteira – os filamentos de vórtices arrastados para o infinito a representa.

Ponto de Controle • Seleção da localização do ponto de controle a partir de uma placa plana com um vórtice colocado a ¼ da corda; • Velocidade normal no ponto x: • Velocidade normal nula no ponto x

Ponto de Controle • Escoamento bidimensional em fluido perfeito: • A pequenos ângulos de ataque; como • Ponto de controle a ¾ da corda (Teorema de Pistolesi):

Desenvolvimento da formulação • • Ref. Bertin & Smith – Aerodynamics for Engineers Velocidade induzida em um ponto P por um vórtice de ferradura, antes apresentou-se o módulo da velocidade: que na realidade é vetorial.

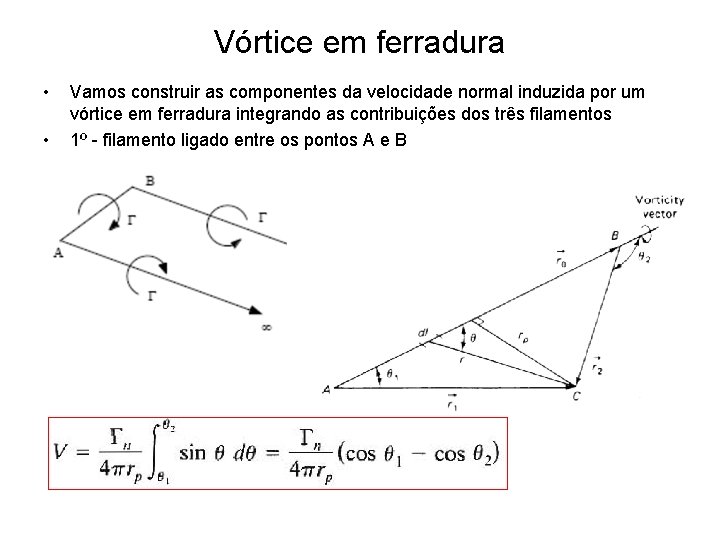
Vórtice em ferradura • • Vamos construir as componentes da velocidade normal induzida por um vórtice em ferradura integrando as contribuições dos três filamentos 1º - filamento ligado entre os pontos A e B

Vórtice em ferradura • E se o filamentos ligado estende-se ao infinito, recupera-se a solução bidimensional para o vórtice ligado ( teoria do aerofólio fino): • pois q 1 = 0 e q 2 = p. AB, AC e BC serão designados por r 0, r 1 e r 2 respectivamente, tal que: • Substituindo : em

Vórtice em ferradura • Expressão básica para o cálculo da velocidade induzida por um vórtice de ferradura VLM: • Para um ponto qauluqer no espaço: • Velocidade induzida em um ponto C

Vórtice em ferradura • C é na realidade C(x, y, z)

Velocidade em um ponto • Para calcular a velocidade do filamento que se estende de A para o infinito, adota-se um ponto D tal que:

Filamento infinito • E situando D na, realidade no infinito, do filamento que sai de A tem-se: e do filamento que sai de B:

Velocidade total induzida • Somando as três contribuições: • Chega-se a velocidade total induzida em (x, y, z): • • Vórtice ferradura no painel “n” Ponto de controle em (xm, ym, zm) Cmn é a matriz de coeficientes de influência; Depende de geometria apenas.

Matriz de coeficiente de influência • Supondo 2 N vórtices de ferradura situados em cada painel: • • Ou seja, temos 2 N equações para cada ponto de controle em (x, y, z) Simplificação para uma asa plana:

Caso plano (Planar) • Como a velocidade induzida é apenas a componente alinhada com a direção “z”: • Downwash induzido nos 2 N pontos de controle:

Condição de Contorno • O que não deixa de representar a tangência do escoamento com relação a superfícies sustentadora: • Ou para pequenos ângulos de ataque: • Permitindo desta forma particularizar a solução do problema, isto é, a e a velocidade do escoamento não perturbado U são conhecidos. O caso apresentado é uma simplificação do caso geral, onde se pressupões que a asa pode ser aproximada por uma placa plana. Pode-se implementar a generalização onde se pode considerar diedro e arqueamento caso não plano (non-planar) Condição de Kutta implicitamente satisfeita quando se assume o vórtice de ferradura com um filamento ligado Esteira: assumida plana, alinhada com o escoamento, e representada pelo potencial da circulação aglutinada nos vórtices arrastados até o infinito. • •

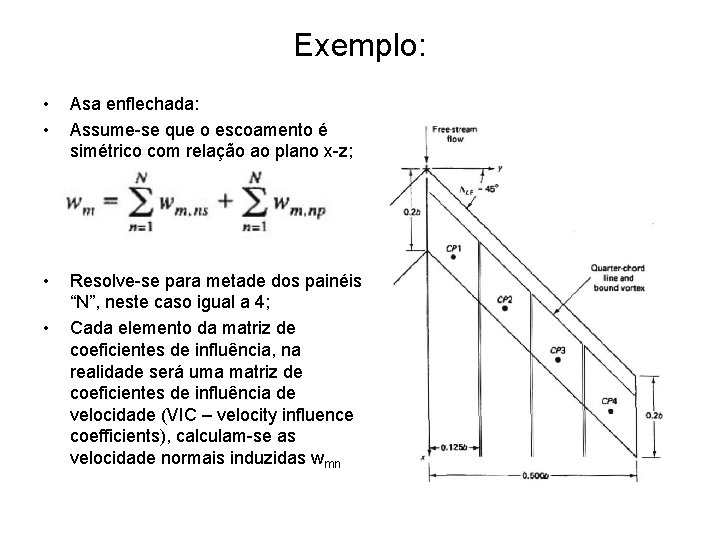
Exemplo: • • Asa enflechada: Assume-se que o escoamento é simétrico com relação ao plano x-z; • Resolve-se para metade dos painéis “N”, neste caso igual a 4; Cada elemento da matriz de coeficientes de influência, na realidade será uma matriz de coeficientes de influência de velocidade (VIC – velocity influence coefficients), calculam-se as velocidade normais induzidas wmn •

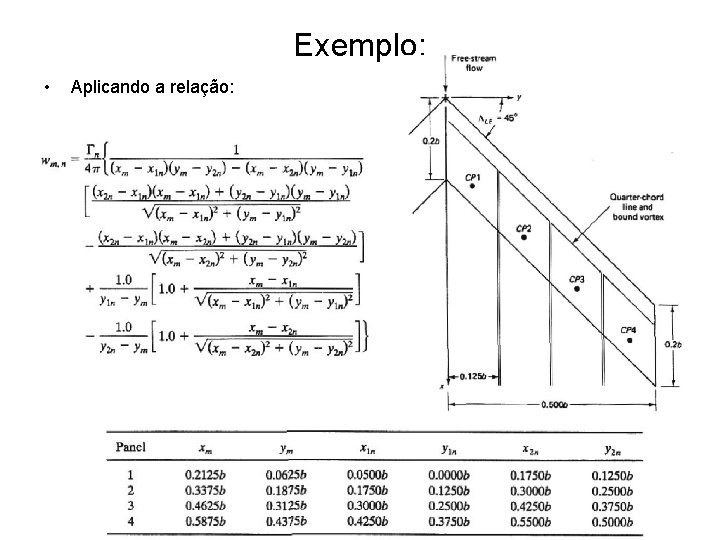
Exemplo: • Aplicando a relação:

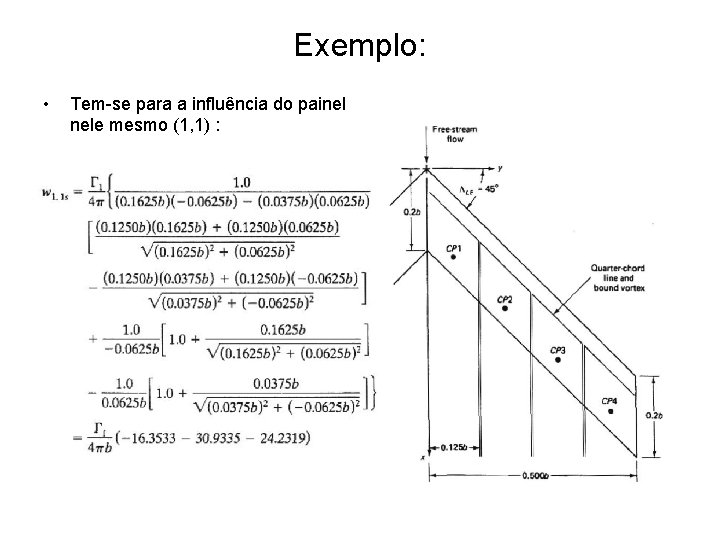
Exemplo: • Tem-se para a influência do painel nele mesmo (1, 1) :

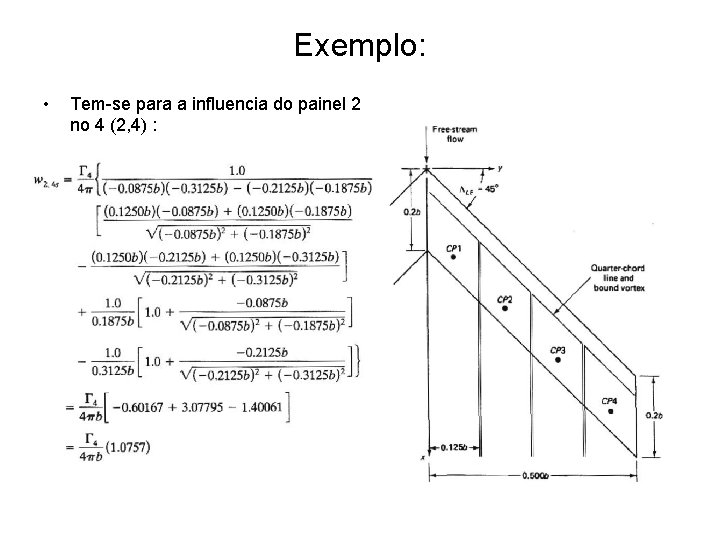
Exemplo: • Tem-se para a influencia do painel 2 no 4 (2, 4) :

Exemplo: • Para cada ponto de controle da asa:

Exemplo: • Aplica-se a condição de contorno, observando que em todos os pontos de controle a velocidade deve ser tangente, ou seja: E assim encerramos o sistema de equações a ser resolvido, de onde se obtém as intensidade de circulação associadas a cada intensidade de vórtice de ferradura:
 Aerodinmica
Aerodinmica Aerodinmica
Aerodinmica Placa plana
Placa plana Avion subsonico
Avion subsonico What is the old regime in france
What is the old regime in france Ancien régime
Ancien régime Old regime french revolution
Old regime french revolution Regime diferenciado disciplinar
Regime diferenciado disciplinar O que é regime de colaboração
O que é regime de colaboração Antigo regime e iluminismo
Antigo regime e iluminismo Regime demografico moderno
Regime demografico moderno Dissection artere mesenterique
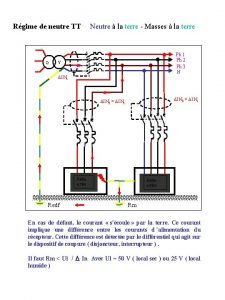
Dissection artere mesenterique Regime de neutre it
Regime de neutre it Flow regime
Flow regime Regime jenny gray
Regime jenny gray Regime diferenciado disciplinar
Regime diferenciado disciplinar Legal regime
Legal regime Propagande vichy
Propagande vichy The flexible exchange rate regime 1973-present
The flexible exchange rate regime 1973-present Divc regime malaysia
Divc regime malaysia Parcours 1
Parcours 1 Pay with taxes
Pay with taxes Self contained regime
Self contained regime Carte mentale staline
Carte mentale staline Guinier regime
Guinier regime Regime sinusoidale
Regime sinusoidale Fluidos
Fluidos Regime douanier
Regime douanier Regime de competencia
Regime de competencia Transistor en regime dynamique
Transistor en regime dynamique First aid pdhpe
First aid pdhpe Old regime 3 estates
Old regime 3 estates Tarasoff rule
Tarasoff rule Regime example
Regime example Errore a regime
Errore a regime Regime alpino
Regime alpino Calculadora projudi
Calculadora projudi Ehrz tb
Ehrz tb Beggs and brill flow regime map
Beggs and brill flow regime map Tabela regime de bens
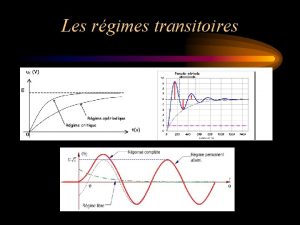
Tabela regime de bens Regime permanente
Regime permanente Albertis regime
Albertis regime Régime it cpi
Régime it cpi Régime permanent et transitoire
Régime permanent et transitoire Regimi finanziari
Regimi finanziari The ancien regime
The ancien regime Ancient regime
Ancient regime Gik regime
Gik regime Simulazione energetica in regime dinamico
Simulazione energetica in regime dinamico Régime hypoprotidique exemple
Régime hypoprotidique exemple