AA209 AERODIN MICA DA ASA E FUSELAGEM EM

AA-209 AERODIN MICA DA ASA E FUSELAGEM EM REGIME SUBSONICO Prof. GIL

Fluido Perfeito/Ideal • Equação da continuidade aplicada a f • Condição de irrotacionalidade aplicada a y • A função potencial f e a função de corrente y obedecem à equação de Laplace • Linhas de corrente são perpendiculares às equipotenciais

Diferenças entre f e y 1. As variáveis do escoamento podes ser obtidas: – Diferenciando f na mesma direção das velocidades – Diferenciando y na direção normal às velocidades 2. Função potencial f aplica-se apenas a escoamento irrotacional 3. Função linha de corrente y aplica-se tanto para escoamento rotacionais quanto irrotacionais 4. Função potencial f aplica-se para escoamento 2 D [f(x, y) ou f(r, q)] e 3 D [f(x, y, z) ou f(r, q, f)] 5. Função linha de corrente y aplica-se apenas em 2 D [y(x, y) ou y(r, q)] 6. Linhas de corrente (y =constante) e linhas equipotenciais (f =constante) são perpendiculares entre si 3

Potencial Complexo • Uma função de variável complexa é uma função analítica quando • existe e o seu valor é independente da forma como z tende para zero • No limite quando Dz 0

Potencial Complexo • Para que o limite seja independente da forma como Dz 0, esta relação tem de ser independente de dy/dx • Condições de Riemann-Cauchy: • Qualquer função W(z) que seja somente função de z é uma função analítica, verificação:

Potencial Complexo • Verificação: • Se a função é analítica:

Potencial Complexo • Exemplos de funções complexas • Funções potencial e linha de corrente: • São analíticas pela sua propria definição:

Potencial complexo • Funções Analíticas – W, função de variável complexa

Potencial complexo • A função potencial complexo é uma função analítica com a parte real igual à função potencial de velocidade e a parte imaginária igual à função de corrente de um escoamento plano incompressível e irrotacional. • E para este potencial complexo, o diferencial d. W pode ser obtido como:

Velocidade complexa • Para o potencial complexo, obtem-se portanto, por diferenciação: O conjugado complexo do vetor velocidade é a velocidade complexa

Exemplos • Escoamento constante

Exemplos • cilindro

Exemplos • Cilindro

Circulação • Considerando um escoamento cujo potencial complexo é dado por W =f + iy • Fluxo por unidade de comprimento

Circulação • Somando os resultados visando obter o potencial complexo associado: • Potencial complexo para uma linha de vortices/fontes

Circulação • Contorno fechado • Onde r é o modulo do vetor (z-z 0) e c é o argumento.

Circulação • Singularidade exterior ao contorno C

Circulação • Singularidade interior ao contorno C

Circulação e Fluxo • Contribuição das singularidades: Gi e Qi representam a soma das intensidades das linhas de vórtices e fontes/sumidouros que se encontram no interior de C

Cálculo de Forças • Forças exercidas por um escoamento planos em torno de um sólido: • Caso de estudo - cilindro circular: • Na superfície do cilindro:

Cilindro sem circulação • Sabendo-se que as forças atuantes em um corpo estão relacionadas a distribuição de pressão sobre o mesmo:

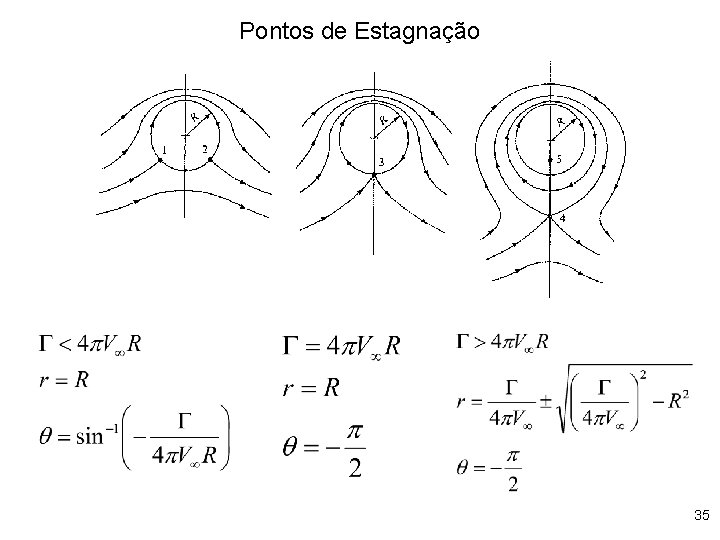
Cilindro com circulação • Incluindo a circulação G: • Pontos de estagnação:

Cilindro com circulação • Pontos de estagnação: Para: Dois pontos de estagnação com a mesma parte imaginária e partes reais simétricas, menores que a Um ponto de estagnação (raíz dupla) no eixo imaginário em –ia Dois pontos de estagnação no eixo imaginário. Um abaixo de -ia e outro no interior do cilindro

Cilindro sem circulação • Sabendo-se que as forças atuantes em um corpo estão relacionadas a distribuição de pressão sobre o mesmo:

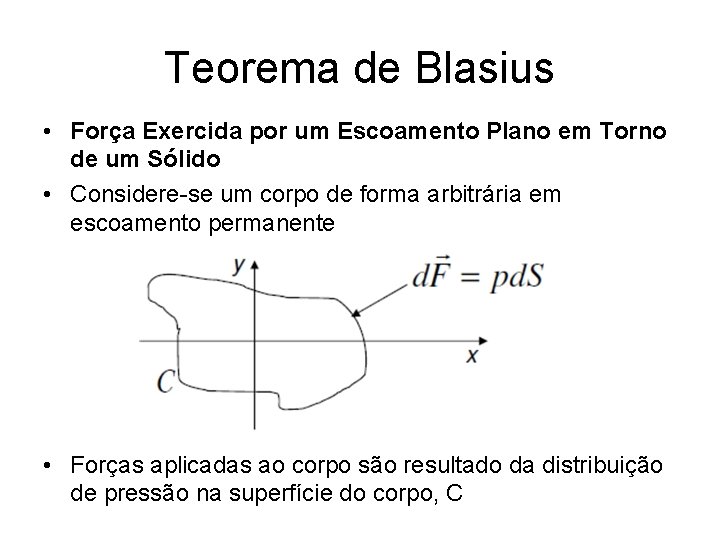
Teorema de Blasius • Força Exercida por um Escoamento Plano em Torno de um Sólido • Considere-se um corpo de forma arbitrária em escoamento permanente • Forças aplicadas ao corpo são resultado da distribuição de pressão na superfície do corpo, C

Teorema de Blasius • Utilizando a equação de Bernoulli e tendo em atenção que o integral ao longo de um contorno fechado de um valor constante (po) não contribui para a força, tem-se:

Teorema de Kutta-Joukowsky • Considere-se a aplicação do teorema de Blasius ao caso de um escoamento uniforme no infinito, em torno de um corpo de forma arbitrária: • Representando o potencial complexo por uma série de Laurent d. W/dz:

Teorema de Kutta-Joukowsky • No infinto z ∞, impoem-se a velocidade: • Tomando como contorno de integração uma circunferência de raio R muito superior às dimensões do corpo e tendo em atenção que não existem singularidades entre a superfície do corpo e o contorno C

Teorema de Kutta-Joukowsky • Q é o somatório das intensidades das linhas de fontes e sumidouros no interior do contorno C • G é o somatório das intensidades das linhas de vórtice no interior do contorno C • M representa o momento complexo resultante das linhas de dipolos no interior do contorno C • A função integranda da equação de Blasius é:

Teorema de Kutta-Joukowsky • Teorema dos resíduos Como: e

Teorema de Kutta-Joukowsky • Substituindo na formula de Blasius:

Teorema de Kutta-Joukowsky • Projetando o vector força nas direções paralela e perpendicular à direção do escoamento perturbado no infinito (z ∞) obtêm-se: • Em escoamento potencial, um corpo finito imerso num escoamento uniforme tem: – Força de arrasto (D) nula – PARADOXO DE D´ALEMBERT – Força de sustentação (L) proporcional à circulação(G) – As forças de arrasto e sustentação são independentes da forma do corpo

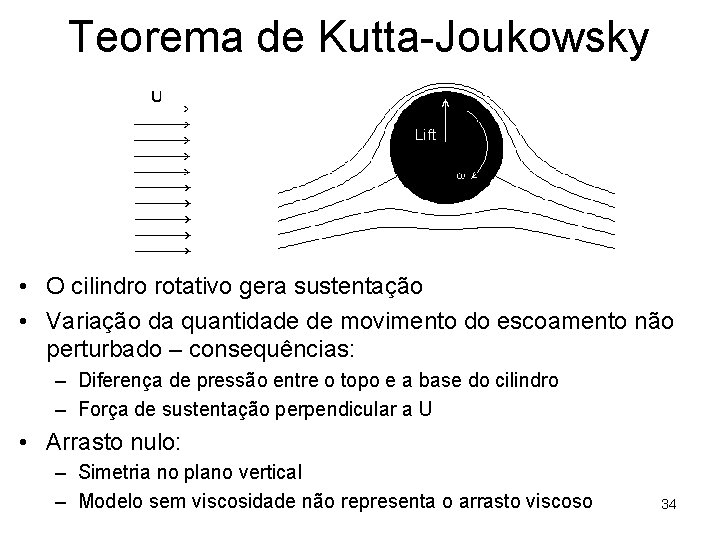
Teorema de Kutta-Joukowsky LIFTING FLOW OVER A CYLINDER Teorema de Kutta-Joukowski 33

Teorema de Kutta-Joukowsky • O cilindro rotativo gera sustentação • Variação da quantidade de movimento do escoamento não perturbado – consequências: – Diferença de pressão entre o topo e a base do cilindro – Força de sustentação perpendicular a U • Arrasto nulo: – Simetria no plano vertical – Modelo sem viscosidade não representa o arrasto viscoso 34

Pontos de Estagnação 35

Tabela 3. 1 do Anderson – resumo das singularidades 2 D- duas dimensões 36

Implicações • Teorema de Blasius – o Teorema de Kutta -Joukowsky aplica-se a corpos cilíndricos de qualquer seção transversal; • A sustentação por unidade de envergadura é proporcional a circulação; • Pode-se afirmar que a distribuição de pressão pé uma consequência da circulação; • A circulação é uma forma alternativa de entender a sustentação: – Fisicamente, o que promove a sustentação é a diferença de pressões distribuídas que são uma consequência do balanço de QDM do escoamento que passa pelo corpo 37

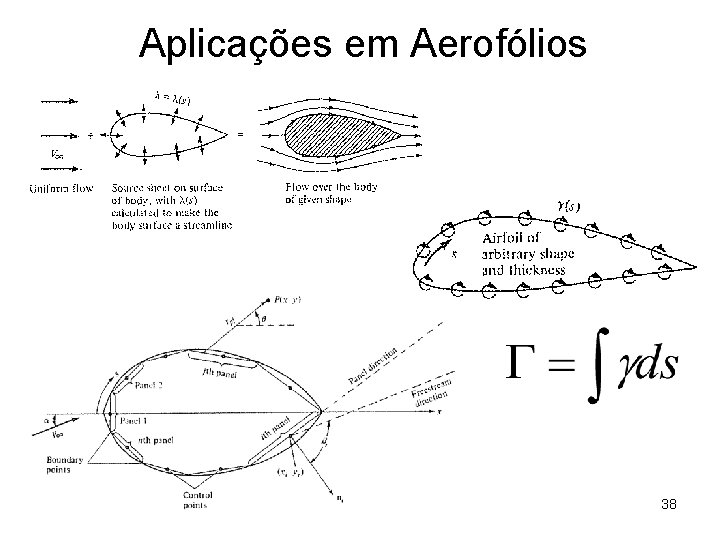
Aplicações em Aerofólios 38