1 campi scalari e vettoriali 2 integrali curvilinei







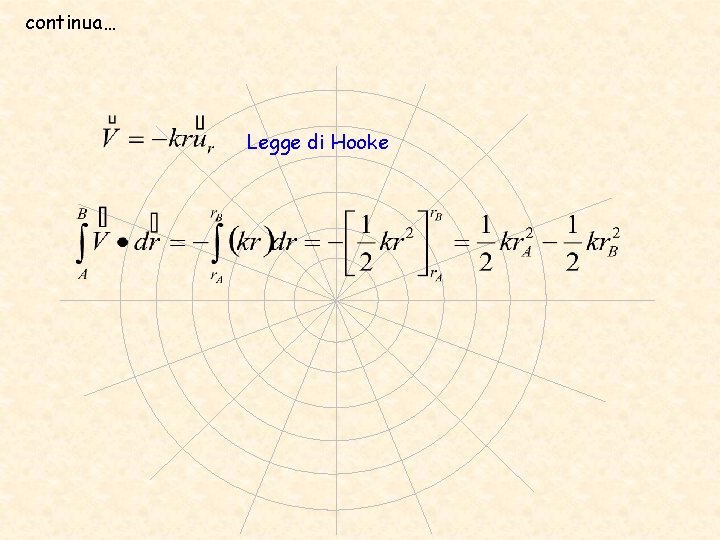
























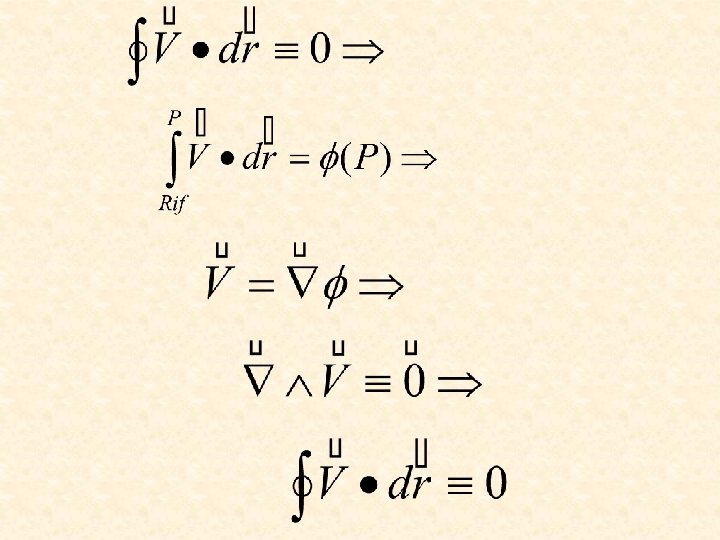


- Slides: 71

1) campi scalari e vettoriali 2) integrali curvilinei di campi vettoriali 3) campi vettoriali irrotazionali 4) curve chiuse e circuitazione di un campo vettoriale 5) l’energia di posizione di una forza conservativa 6) teorema dell’energia cinetica per forze conservative 7) il gradiente di un campo scalare 8) l’operatore “nabla” 9) gradiente, divergenza e rotore (grad, div, rot) 10) riassunto

1) Campi scalari e vettoriali

campi vettoriali (in ogni punto un vettore): • • • campo campo (e. g. • campo di forze gravitazionale elettrico magnetico di velocità di un fluido) dei venti (meteo) campi scalare (in ogni punto un numero): • • • temperatura T(x, y, z, t) pressione P(x, y, z, t) esposizione esp(x, y, z, t) altezza sul mare (x, y) massa (x, y, z, t)

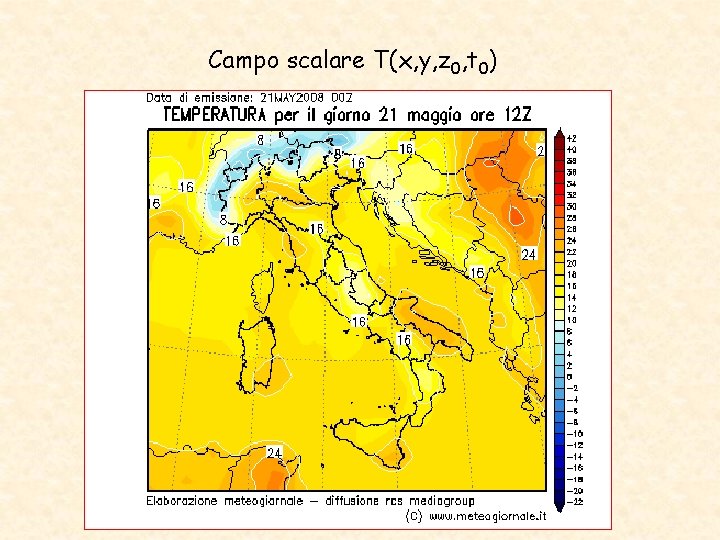
Campo scalare T(x, y, z 0, t 0)

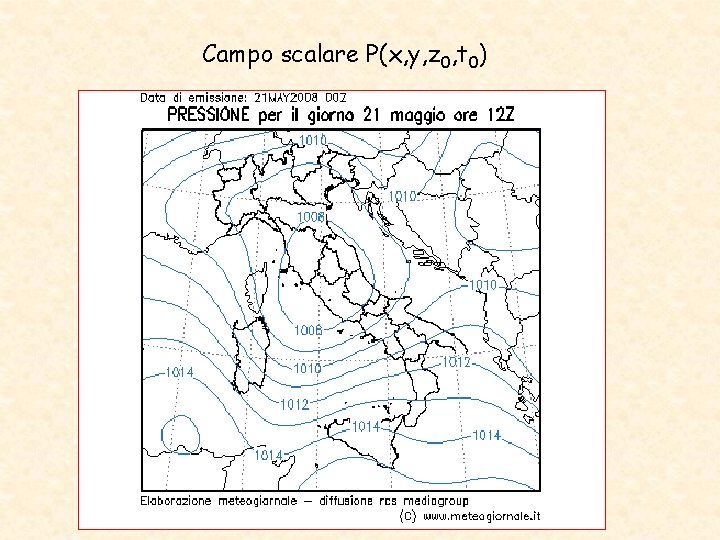
Campo scalare P(x, y, z 0, t 0)

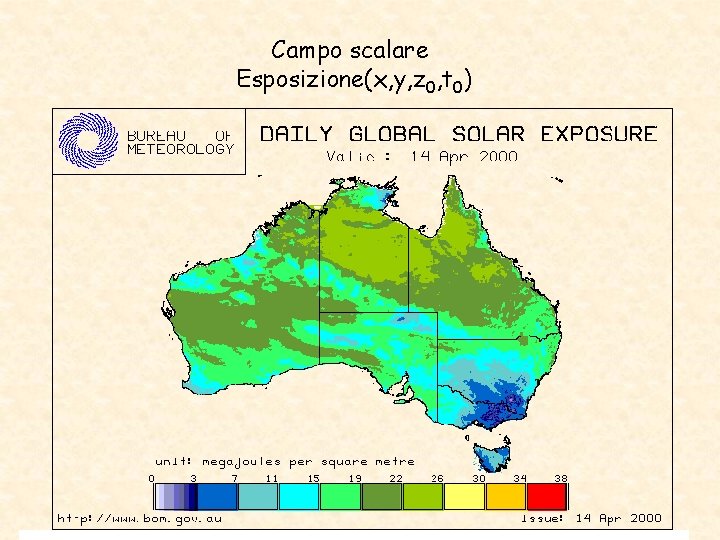
Campo scalare Esposizione(x, y, z 0, t 0)

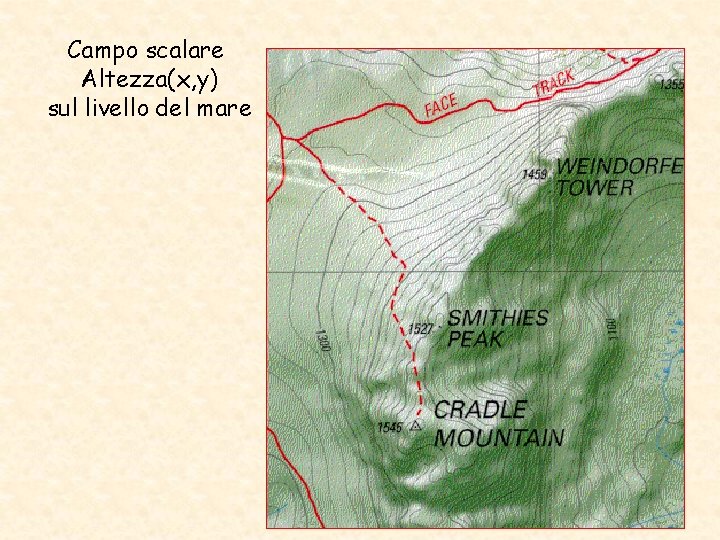
Campo scalare Altezza(x, y) sul livello del mare

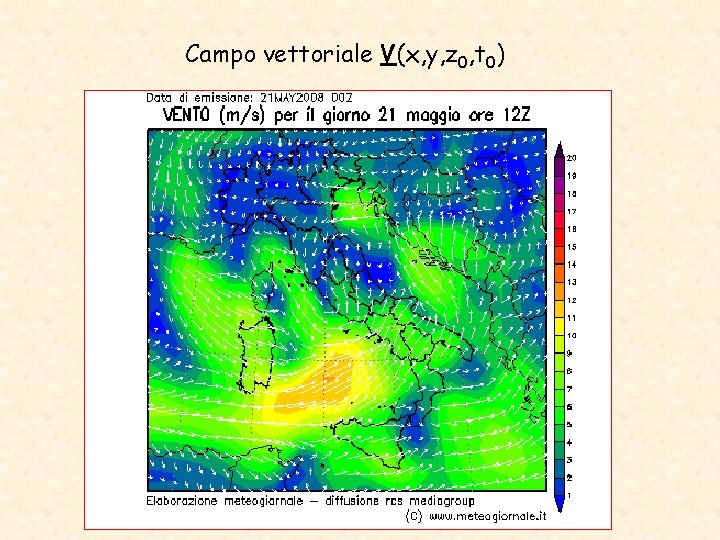
Campo vettoriale V(x, y, z 0, t 0)

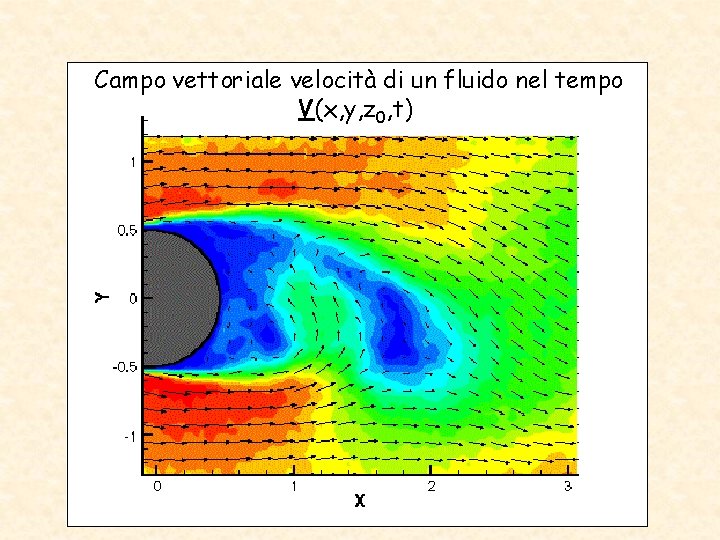
Campo vettoriale velocità di un fluido nel tempo V(x, y, z 0, t) <>

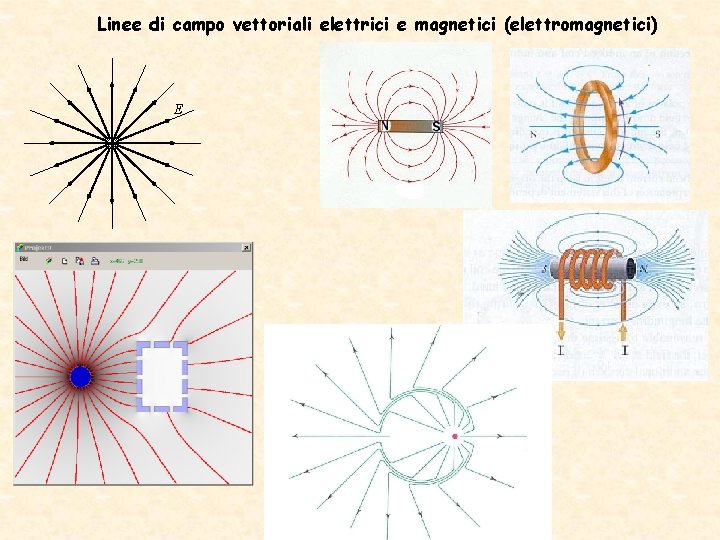
Linee di campo vettoriali elettrici e magnetici (elettromagnetici) E

2) L’integrale curvilineo di un campo vettoriale

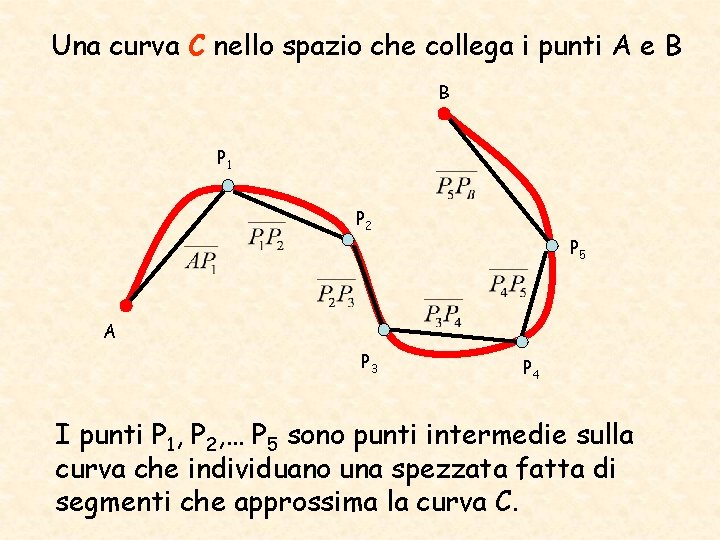
Una curva C nello spazio che collega i punti A e B B P 1 P 2 P 5 A P 3 P 4 I punti P 1, P 2, … P 5 sono punti intermedie sulla curva che individuano una spezzata fatta di segmenti che approssima la curva C.

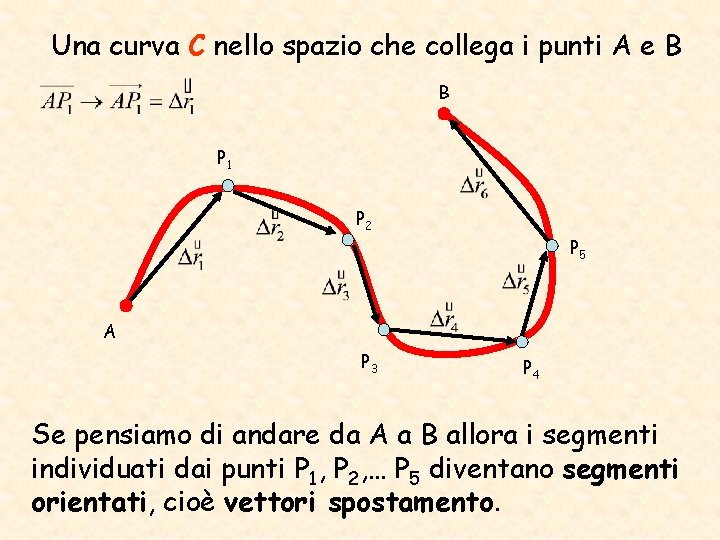
Una curva C nello spazio che collega i punti A e B B P 1 P 2 P 5 A P 3 P 4 Se pensiamo di andare da A a B allora i segmenti individuati dai punti P 1, P 2, … P 5 diventano segmenti orientati, cioè vettori spostamento.

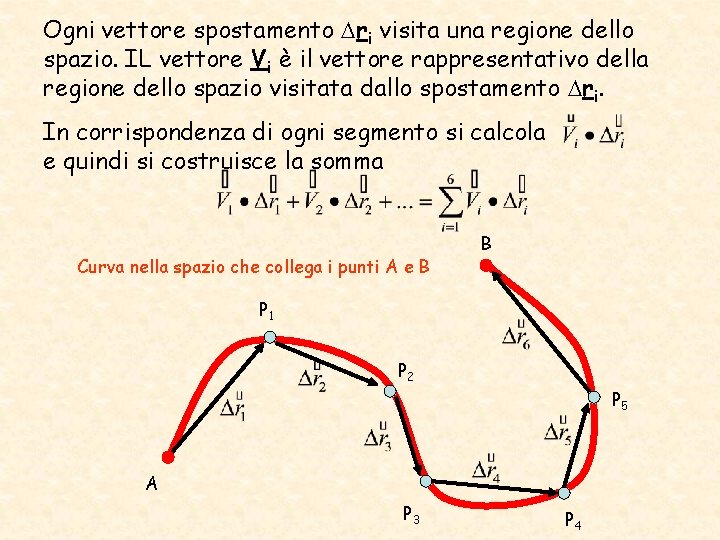
Ogni vettore spostamento ri visita una regione dello spazio. IL vettore Vi è il vettore rappresentativo della regione dello spazio visitata dallo spostamento ri. In corrispondenza di ogni segmento si calcola e quindi si costruisce la somma Curva nella spazio che collega i punti A e B B P 1 P 2 P 5 A P 3 P 4

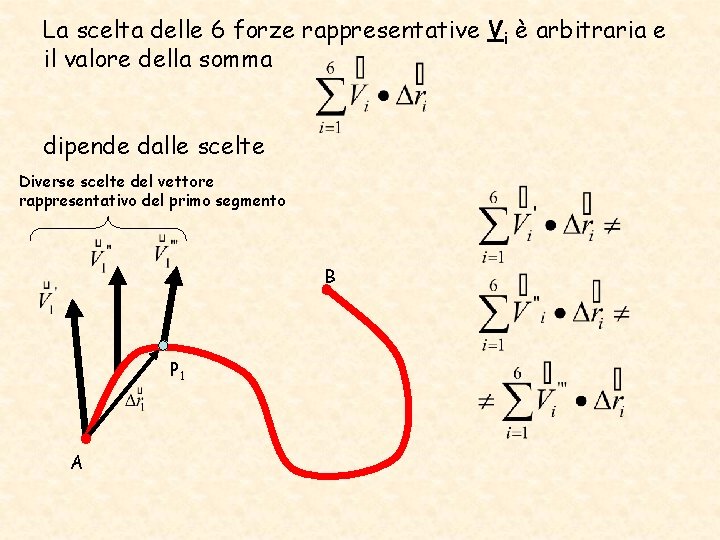
La scelta delle 6 forze rappresentative Vi è arbitraria e il valore della somma dipende dalle scelte Diverse scelte del vettore rappresentativo del primo segmento B P 1 A

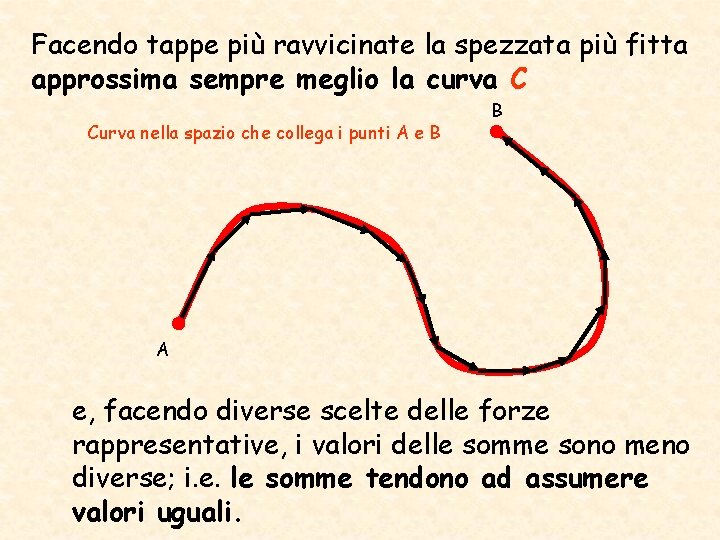
Facendo tappe più ravvicinate la spezzata più fitta approssima sempre meglio la curva C Curva nella spazio che collega i punti A e B B A e, facendo diverse scelte delle forze rappresentative, i valori delle somme sono meno diverse; i. e. le somme tendono ad assumere valori uguali.

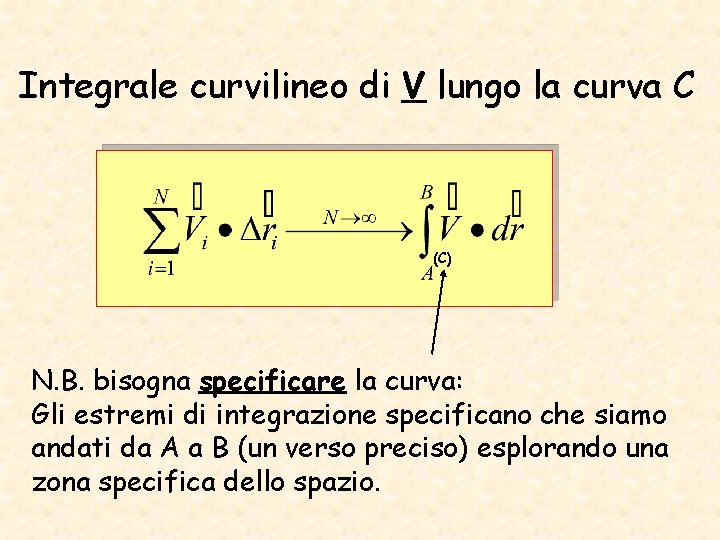
Integrale curvilineo di V lungo la curva C (C) N. B. bisogna specificare la curva: Gli estremi di integrazione specificano che siamo andati da A a B (un verso preciso) esplorando una zona specifica dello spazio.

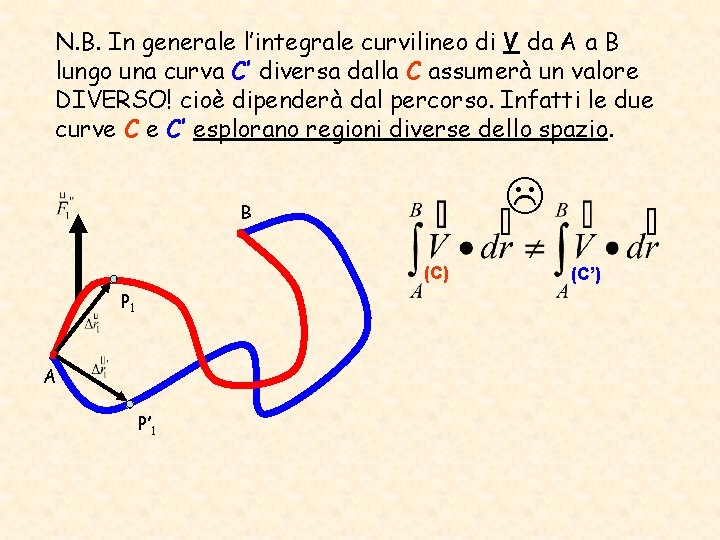
N. B. In generale l’integrale curvilineo di V da A a B lungo una curva C’ diversa dalla C assumerà un valore DIVERSO! cioè dipenderà dal percorso. Infatti le due curve C e C’ esplorano regioni diverse dello spazio. B (C) P 1 A P’ 1 (C’)

3) Campi vettoriali irrotazionali (“conservativi”)

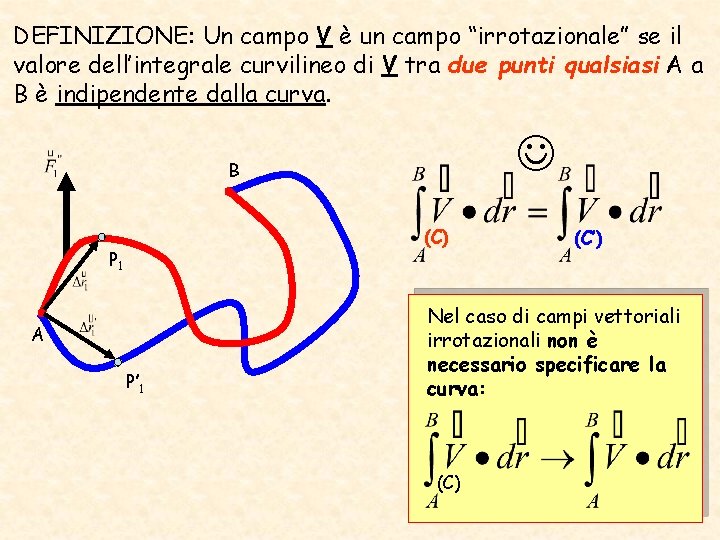
DEFINIZIONE: Un campo V è un campo “irrotazionale” se il valore dell’integrale curvilineo di V tra due punti qualsiasi A a B è indipendente dalla curva. B (C) P 1 A P’ 1 (C’) Nel caso di campi vettoriali irrotazionali non è necessario specificare la curva: (C)

Ma i campi irrotazionali esistono per davvero, o la definizione è vuota? Se esistono allora fammi un esempio!

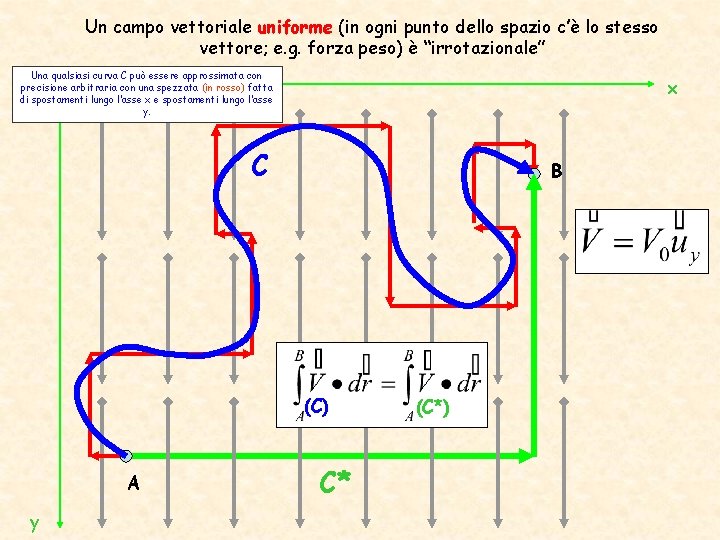
Un campo vettoriale uniforme (in ogni punto dello spazio c’è lo stesso vettore; e. g. forza peso) è “irrotazionale” Una qualsiasi curva C può essere approssimata con precisione arbitraria con una spezzata (in rosso) fatta di spostamenti lungo l’asse x e spostamenti lungo l’asse y. x C B (C) A y C* (C*)

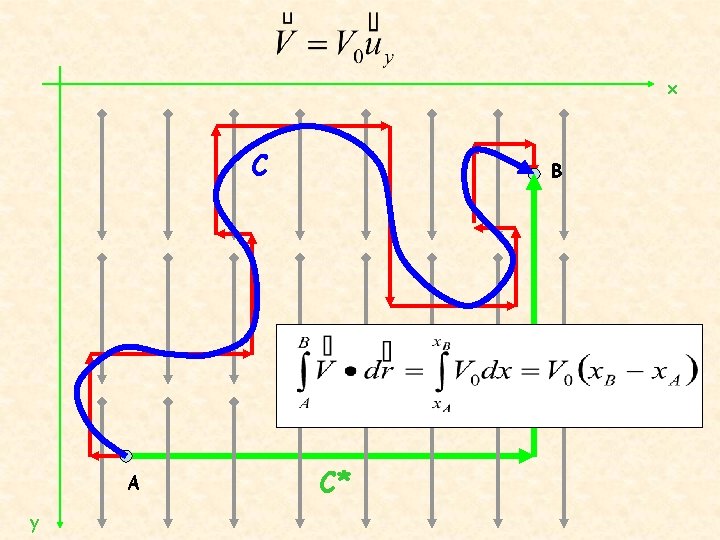
x C A y B C*

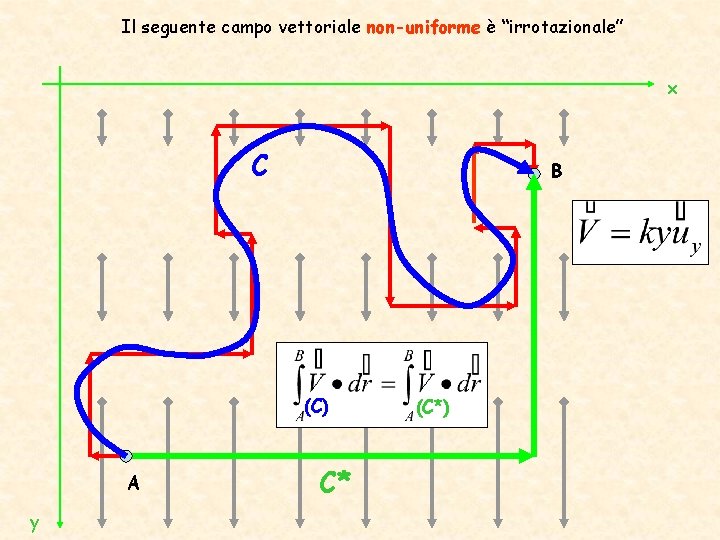
Il seguente campo vettoriale non-uniforme è “irrotazionale” x C B (C) A y C* (C*)

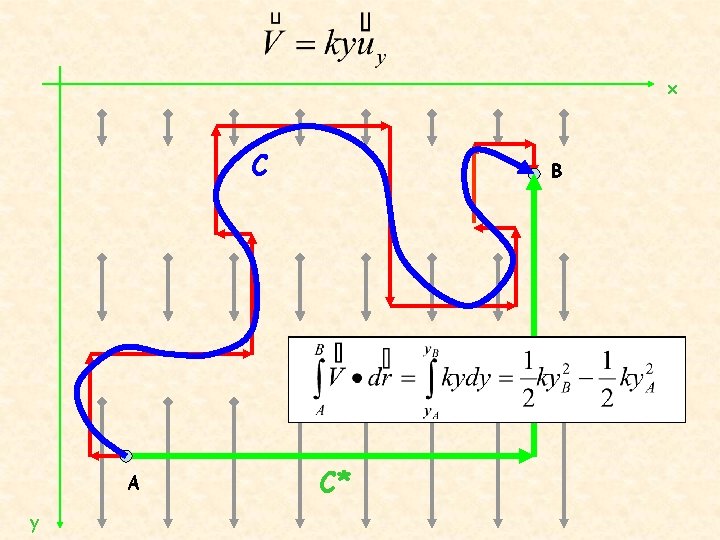
x C A y B C*

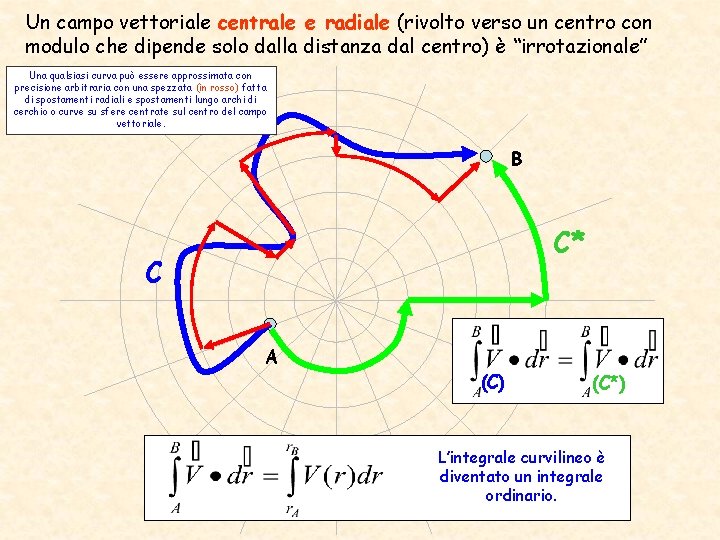
Un campo vettoriale centrale e radiale (rivolto verso un centro con modulo che dipende solo dalla distanza dal centro) è “irrotazionale” Una qualsiasi curva può essere approssimata con precisione arbitraria con una spezzata (in rosso) fatta di spostamenti radiali e spostamenti lungo archi di cerchio o curve su sfere centrate sul centro del campo vettoriale. B C* C A (C) (C*) L’integrale curvilineo è diventato un integrale ordinario.

Campo centrale e radiale è un tipo di campo molto importante: Forza di Gravitazione Universale (Newton) Forza elettrostatica (Coulomb) continua…
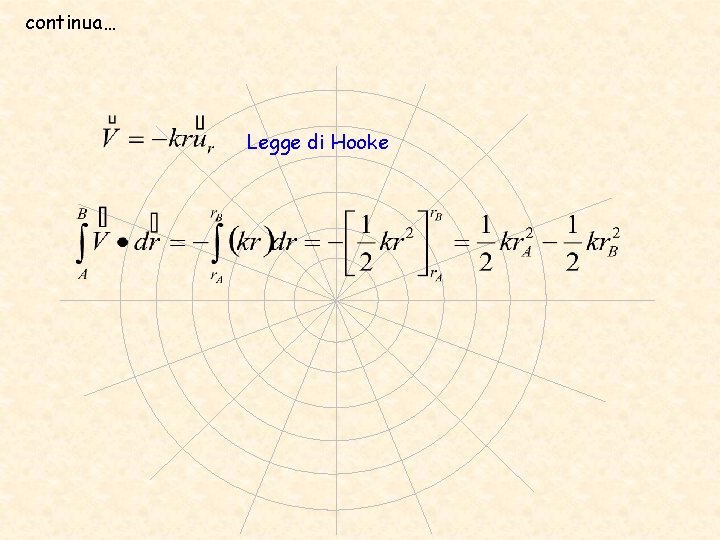
continua… Legge di Hooke

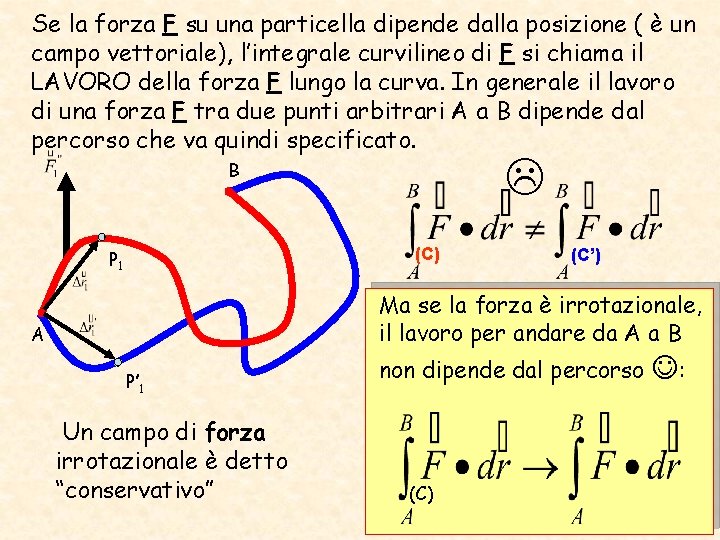
Se la forza F su una particella dipende dalla posizione ( è un campo vettoriale), l’integrale curvilineo di F si chiama il LAVORO della forza F lungo la curva. In generale il lavoro di una forza F tra due punti arbitrari A a B dipende dal percorso che va quindi specificato. B (C) P 1 (C’) Ma se la forza è irrotazionale, il lavoro per andare da A a B A P’ 1 Un campo di forza irrotazionale è detto “conservativo” non dipende dal percorso (C) :

4) Curve chiuse e “circuitazioni” di campi vettoriali

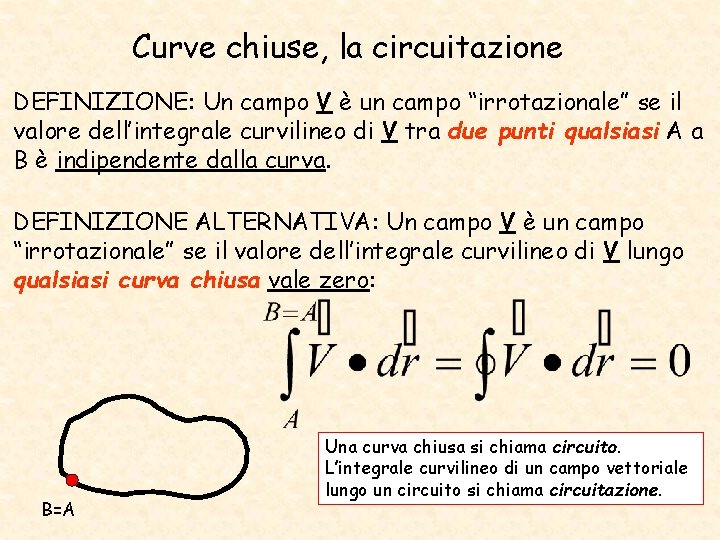
Curve chiuse, la circuitazione DEFINIZIONE: Un campo V è un campo “irrotazionale” se il valore dell’integrale curvilineo di V tra due punti qualsiasi A a B è indipendente dalla curva. DEFINIZIONE ALTERNATIVA: Un campo V è un campo “irrotazionale” se il valore dell’integrale curvilineo di V lungo qualsiasi curva chiusa vale zero: B=A Una curva chiusa si chiama circuito. L’integrale curvilineo di un campo vettoriale lungo un circuito si chiama circuitazione.

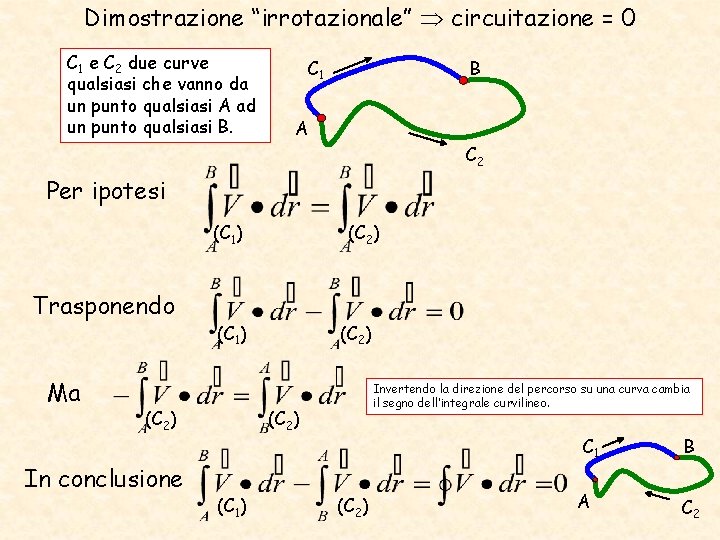
Dimostrazione “irrotazionale” circuitazione = 0 C 1 e C 2 due curve qualsiasi che vanno da un punto qualsiasi A ad un punto qualsiasi B. C 1 B A C 2 Per ipotesi (C 1) Trasponendo Ma (C 1) (C 2) In conclusione (C 2) Invertendo la direzione del percorso su una curva cambia il segno dell’integrale curvilineo. (C 2) (C 1) C 1 (C 2) A B C 2

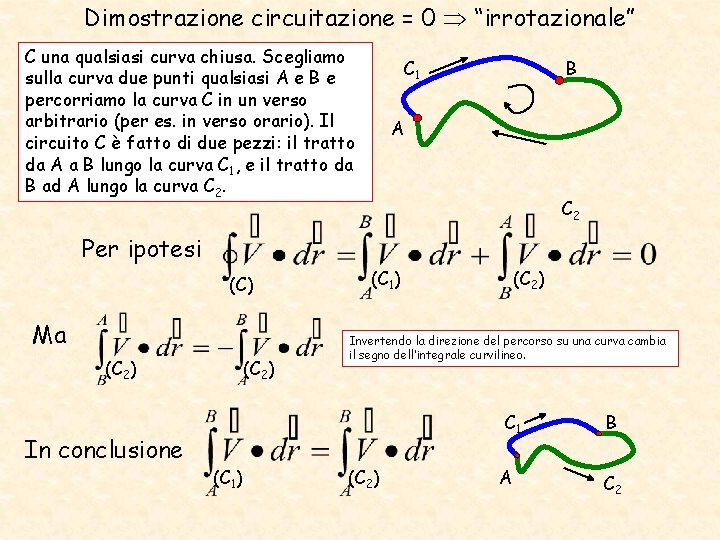
Dimostrazione circuitazione = 0 “irrotazionale” C una qualsiasi curva chiusa. Scegliamo sulla curva due punti qualsiasi A e B e percorriamo la curva C in un verso arbitrario (per es. in verso orario). Il circuito C è fatto di due pezzi: il tratto da A a B lungo la curva C 1, e il tratto da B ad A lungo la curva C 2. C 1 B A C 2 Per ipotesi (C) Ma (C 2) In conclusione (C 2) (C 1) (C 2) Invertendo la direzione del percorso su una curva cambia il segno dell’integrale curvilineo. C 1 (C 1) (C 2) A B C 2

5) L’energia di posizione U di una forza irrotazionale cioè “conservativa”

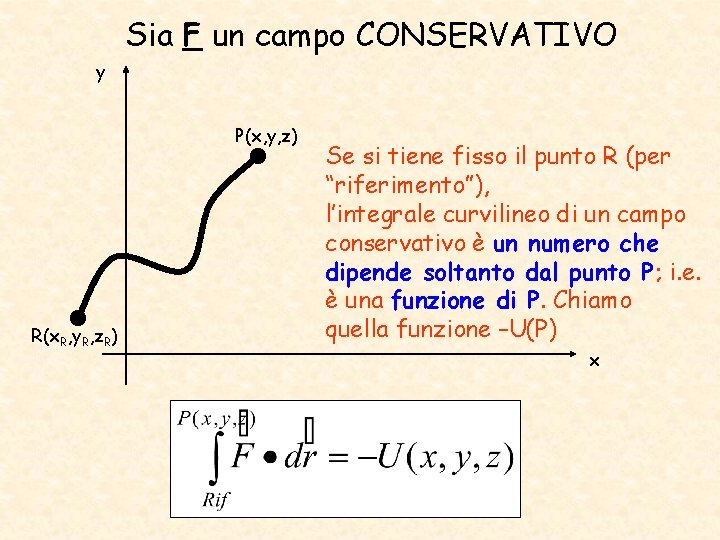
Sia F un campo CONSERVATIVO y P(x, y, z) R(x. R, y. R, z. R) Se si tiene fisso il punto R (per “riferimento”), l’integrale curvilineo di un campo conservativo è un numero che dipende soltanto dal punto P; i. e. è una funzione di P. Chiamo quella funzione –U(P) x

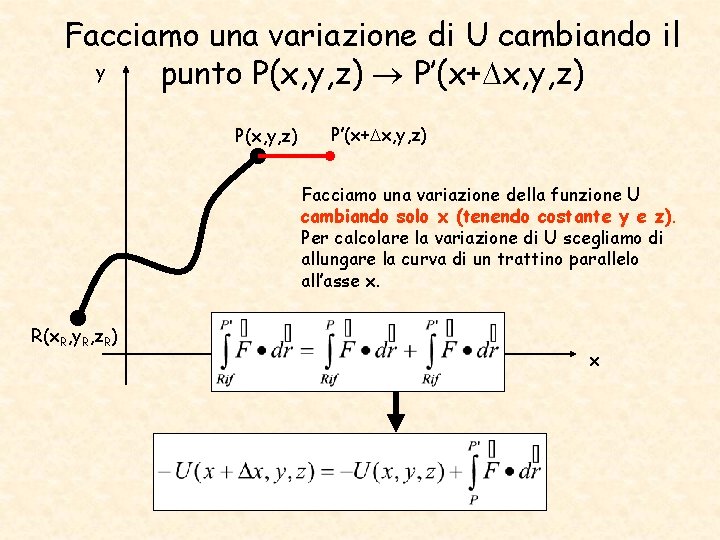
Facciamo una variazione di U cambiando il y punto P(x, y, z) P’(x+ x, y, z) P(x, y, z) P’(x+ x, y, z) Facciamo una variazione della funzione U cambiando solo x (tenendo costante y e z). Per calcolare la variazione di U scegliamo di allungare la curva di un trattino parallelo all’asse x. R(x. R, y. R, z. R) x

Rapporto incrementale di U nella direzione x y P(x, y, z) R(x. R, y. R, z. R) P’(x+ x, y, z) Per il teorema della media con quindi x

La derivata parziale rispetto ad x di U quindi

Le derivate parziali di U cioè

L’operatore “nabla” ATTENZIONE: questa è l’espressione del operatore nabla in coordinate cartesiane ortonormali.

Espressione differenziale (derivate) Una forza conservativa F è il gradiente di una opportuna funzione scalare U, cambiato di segno. La funzione U è chiamata energia di posizione associata alla forza F. La variazione dell’energia di posizione U tra due punti nello spazio è data dall’integrale curvilineo di F calcolato lungo qualsiasi curva che colleghi i due punti, cambiata di segno. Espressione integrale

Perché i campi di vettoriali di forza irrotazionali sono chiamati “conservativi”?

6) Teorema dell’energia cinetica per forze conservative

Per il teorema dell’energia cinetica, di validità generale, la variazione dell’energia cinetica K di una particella di massa m è uguale al lavoro della forza totale WA B calcolato lungo la traiettoria vera (quella data risolvendo l’equazione di Newton) che collega la posizione iniziale A a quella finale B Se la forza Ftot è conservativa allora il lavoro si può calcolare lungo qualsiasi curva che colleghi A e B; i. e. non serve conoscere la traiettoria vera. Sia U l’energia di posizione associata alla forza Ftot è chiamata energia potenziale:

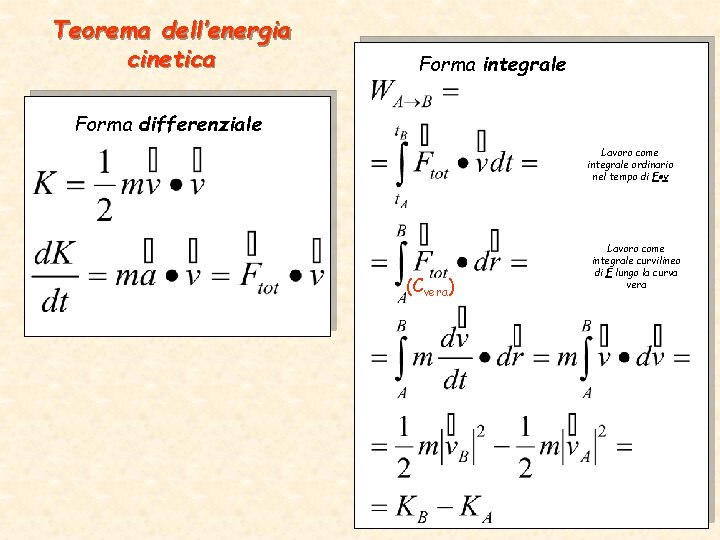
Teorema dell’energia cinetica Forma integrale Forma differenziale Lavoro come integrale ordinario nel tempo di F v (Cvera) Lavoro come integrale curvilineo di F lungo la curva vera

Quindi se la forza totale è conservativa si ha quindi cioè l’energia meccanica è una costante del moto; i. e. l’energia meccanica “si conserva” nel tempo.

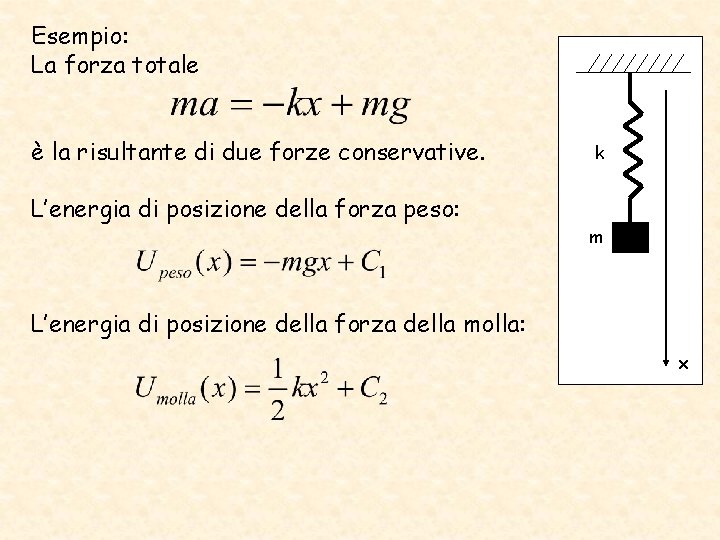
Esempio: La forza totale è la risultante di due forze conservative. L’energia di posizione della forza peso: k m L’energia di posizione della forza della molla: x

L’energia potenziale della forza totale è k La conservazione dell’energia meccanica: esplicitamente è m x

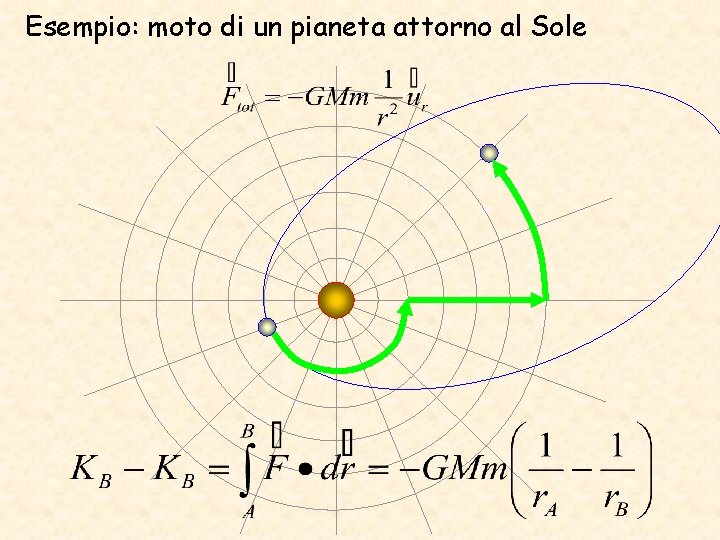
Esempio: moto di un pianeta attorno al Sole

L’energia di posizione della forza di gravitazione universale è: Nel problema del moto del pianeta la conservazione dell’energia meccanica esplicitamente è:

7) Il gradiente di una funzione scalare

Il gradiente di una funzione scalare • estensione del concetto di pendenza • è un vettore che punta nella direzione di massima variazione di una funzione scalare

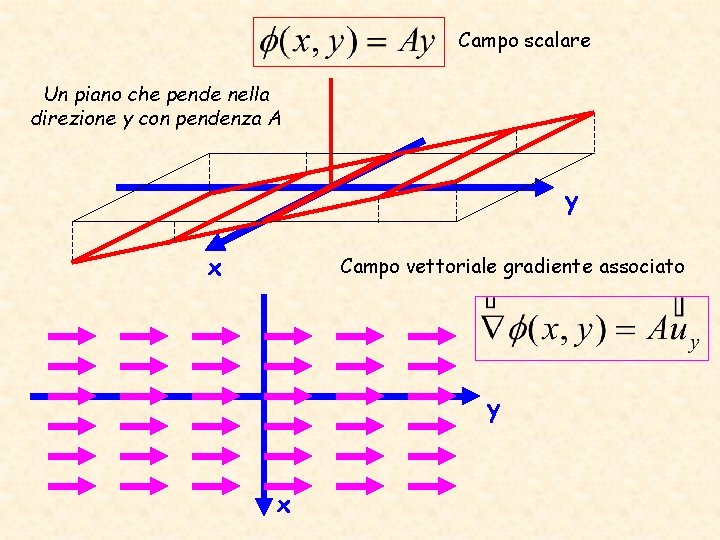
Campo scalare Un piano che pende nella direzione y con pendenza A y x Campo vettoriale gradiente associato y x

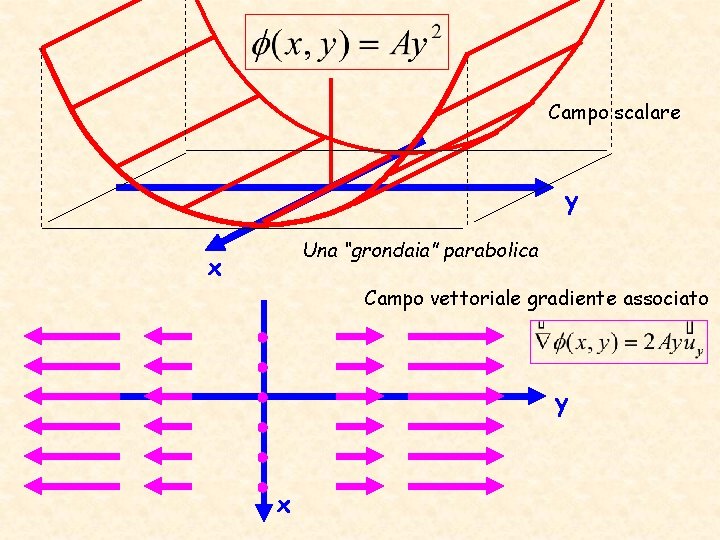
Campo scalare y Una “grondaia” parabolica x Campo vettoriale gradiente associato y x



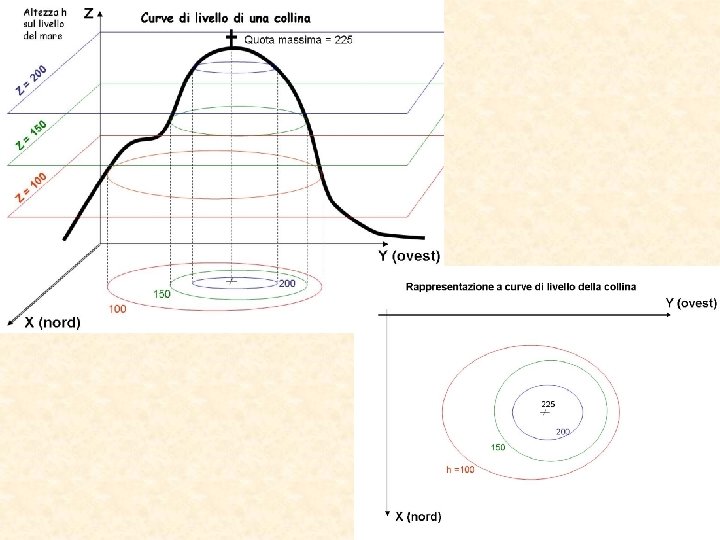
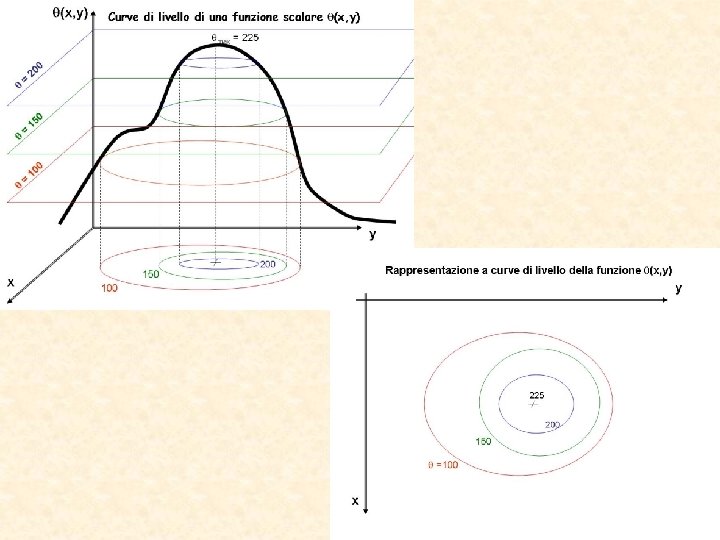
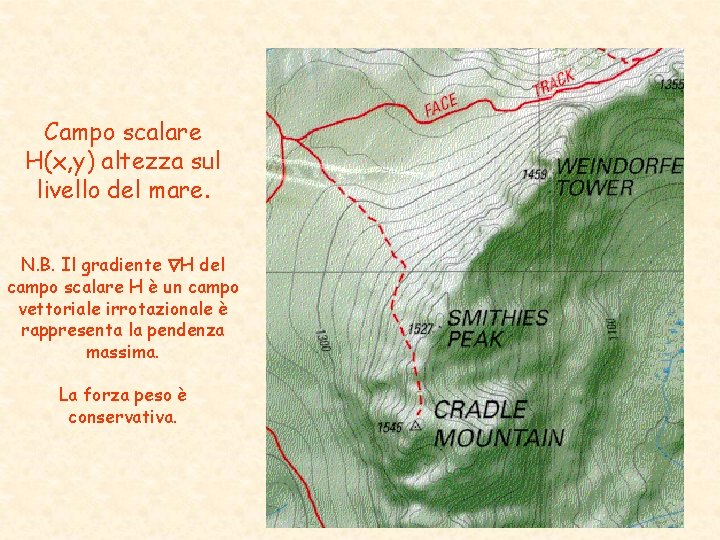
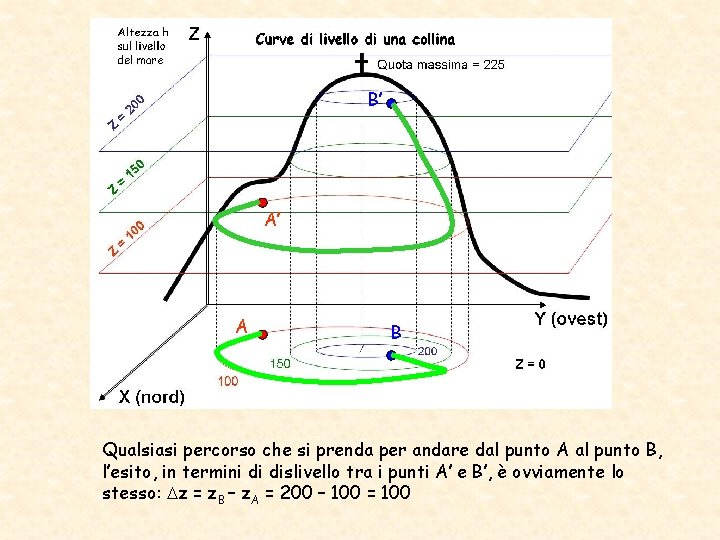
Campo scalare H(x, y) altezza sul livello del mare. N. B. Il gradiente H del campo scalare H è un campo vettoriale irrotazionale è rappresenta la pendenza massima. La forza peso è conservativa.

Il gradiente di una qualsiasi funzione scalare è un campo vettoriale irrotazionale (conservativo se la funzione scalare è una energia potenziale)! (C) indipendentemente dal percorso. Ovviamente (C)

B’ A’ A B Qualsiasi percorso che si prenda per andare dal punto A al punto B, l’esito, in termini di dislivello tra i punti A’ e B’, è ovviamente lo stesso: z = z. B – z. A = 200 – 100 = 100

8) l’operatore nabla

L’operatore vettoriale “nabla” ATTENZIONE: questa è l’espressione del operatore nabla in coordinate cartesiane ortonormali. • si trasforma per rotazioni come un vettore • va manipolato formalmente come un vettore (prodotto scalare, prodotto vettore) • a partire da esso: q gradiente q divergenza q rotore Si giustifica la notazione vettoriale (la freccia!)

9) grad, div, rot

grad, div, rot

Riassunto campi vettoriali conservativi DEFINIZIONE: Un campo V è un campo “irrotazionale” se il valore dell’integrale curvilineo di V tra due punti arbitrari A a B è indipendente dalla curva. DEFINIZIONE ALTERNATIVA: Un campo V è un campo “irrotazionale” se il valore dell’integrale curvilineo di V lungo qualsiasi curva chiusa vale zero: DEFINIZIONE ALTERNATIVA: Un campo V è un campo “irrotazionale” se esiste una funzione scalare tale che V = grad . DEFINIZIONE ALTERNATIVA: Un campo V è un campo “irrotazionale” se il rotore di V è identicamente zero (vettore nullo):

Sia V un campo “irrotazionale”, e quindi esiste un campo scalare con V = grad . Allora rot V = 0 Dimostrazione: N. B. questo teorema è facile da ricordare. Basta prendere sul serio l’idea che l’operatore nabla è un vettore e ricordare che il prodotto vettore di un vettore per se stesso è nullo.

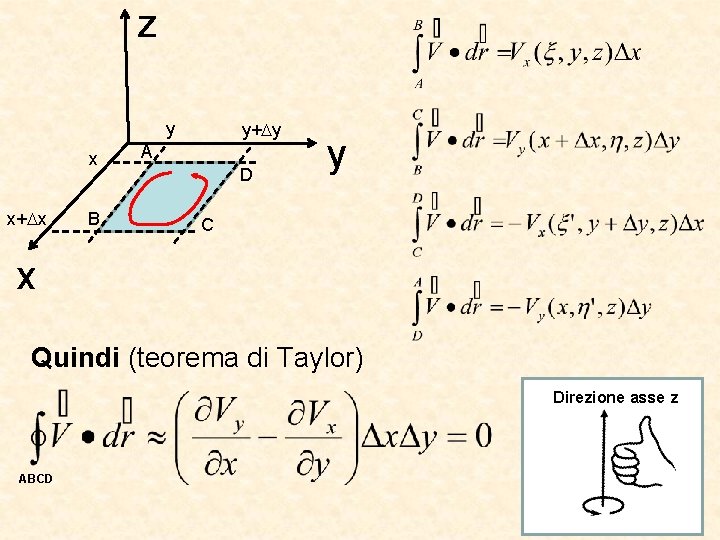
Sia V un campo con un rotore identicamente nullo rot V = 0. Allora il campo V ha circuitazione nulla su qualsiasi curva chiusa. Dimostrazione: Consideriamo una curva chiusa nel piano xy (come in figura) di forma rettangolare con lati piccoli a piacere … z y x x+ x x B y+ y A D C y

z y x x+ x B y+ y A D y C x Quindi (teorema di Taylor) Direzione asse z ABCD

10) riassunto
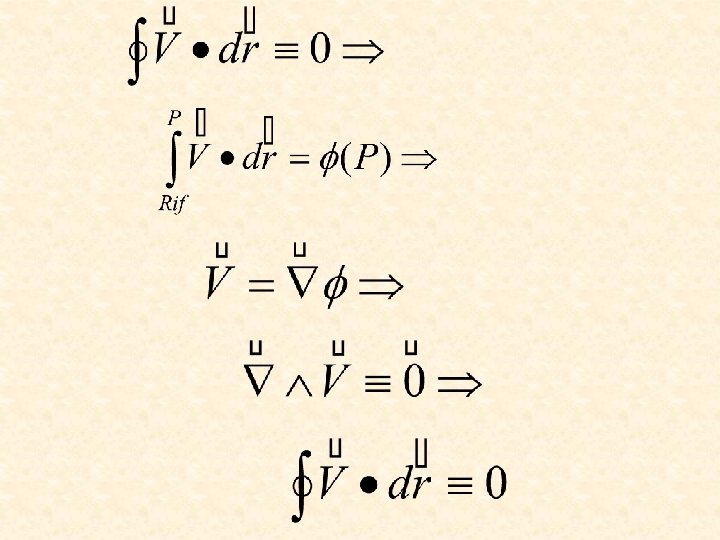

Campo V irrotazionale: affermazioni equivalenti Circuitazione identicamente nulla campo vettoriale associato al campo irrotazionale V Rotore identicamente nullo

forze conservative DEFINIZIONE: Una forza F è “CONSERVATIVA” se il valore dell’integrale curvilineo di F tra due punti arbitrari A a B è indipendente dalla curva. DEFINIZIONE ALTERNATIVA: Un campo F è una forza “CONSERVATIVA” se il valore dell’integrale curvilineo di F lungo qualsiasi curva chiusa vale zero: DEFINIZIONE ALTERNATIVA: Una forza F è “CONSERVATIVA” se esiste una funzione scalare U, detta energia di posizione, tale che F = -grad U. DEFINIZIONE ALTERNATIVA: Una forza F è “CONSERVATIVA” se il rotore di F vale zero (vettore nullo):
 Campi scalari e vettoriali
Campi scalari e vettoriali Integrali curvilinei
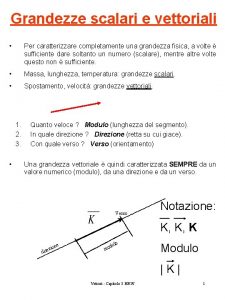
Integrali curvilinei Grandezze scalari e vettoriali
Grandezze scalari e vettoriali Trigonometria formule
Trigonometria formule Campi vettoriali
Campi vettoriali Implicature scalari
Implicature scalari Implicature scalari
Implicature scalari Implicature scalari
Implicature scalari Entailment and implicature
Entailment and implicature Grandezza scalare
Grandezza scalare Implicature scalari
Implicature scalari Campi semantici
Campi semantici I campi d'esperienza
I campi d'esperienza Commento della poesia solo et pensoso
Commento della poesia solo et pensoso Alessandro campi polimi
Alessandro campi polimi Campi di esperienza scuola infanzia
Campi di esperienza scuola infanzia Cristina campi unige
Cristina campi unige La mia bambina con la palla in mano
La mia bambina con la palla in mano Esperimento di oersted zanichelli
Esperimento di oersted zanichelli Orientamenti scuola infanzia
Orientamenti scuola infanzia Rotoloni per irrigazione campi sportivi
Rotoloni per irrigazione campi sportivi Slidetodoc
Slidetodoc Dyor nedir
Dyor nedir Formula fondamentale del calcolo integrale
Formula fondamentale del calcolo integrale Integrali polinomi
Integrali polinomi Integrale senxcosx
Integrale senxcosx Toni milun derivacije
Toni milun derivacije Određeni integral definicija
Određeni integral definicija Integrale di linea
Integrale di linea Modello a sandwich membrana plasmatica
Modello a sandwich membrana plasmatica Integrali mappa concettuale
Integrali mappa concettuale Newton diferansiyel ve integral hesabı
Newton diferansiyel ve integral hesabı Applicazioni integrali alla fisica
Applicazioni integrali alla fisica Integrali formule
Integrali formule Trigonometrik fonksiyonların türevi
Trigonometrik fonksiyonların türevi Dvojni integrali
Dvojni integrali Integrali formule
Integrali formule Pravila za integriranje
Pravila za integriranje Sayısal türev
Sayısal türev Coordinate cilindriche jacobiano
Coordinate cilindriche jacobiano Definizione di primitiva
Definizione di primitiva Disinfestanti integrali
Disinfestanti integrali Carboidrati integrali
Carboidrati integrali Primena izvoda
Primena izvoda Formule di riduzione
Formule di riduzione