Twolevel Logic Synthesis and Optimization Giovanni De Micheli

Two-level Logic Synthesis and Optimization Giovanni De Micheli Integrated Systems Laboratory This presentation can be used for non-commercial purposes as long as this note and the copyright footers are not removed © Giovanni De Micheli – All rights reserved

Module 1 u Objectives s Fundamentals of logic synthesis s Mathematical formulation s Definition of the problems (c) Giovanni De Micheli 2

What is logic synthesis? u A logic-level representation is: s A Boolean function s A set of Boolean functions and their dependences s A schematic with logic gates s A logic-level HDL description u Logic synthesis is the process of optimizing logic representations with the final goal of: s Speeding up a circuit s Reducing its area and manufacturing cost s Reducing the energy consumption (c) Giovanni De Micheli 3

Logic synthesis has a long history u George Boole: s Boolean Algebra u Claude Shannon s Switching Theory u Modern logic synthesis s Ed Mc. Cluskey, Robert Brayton, Randy Bryant t … and many other noteworthy scientists (c) Giovanni De Micheli 4

Combinational logic design Background u Boolean Algebra s Quintuple (B, +, . , 0, 1) s Binary Boolean algebra B = { 0, 1 } u Boolean function s Single output f : Bn → B s Multiple output f : Bn → Bm s Incompletely-specified: t t Don’t care symbol: * f : Bn → { 0, 1, * }m (c) Giovanni De Micheli 5

Examples of Boolean Algebras u Algebra of classes: s Universal set S – classes are subsets of S s 2 S set of subsets of S s Quintuple (2 S, U, Π , Ø, S) u Arithmetic Boolean algebra s n = product of distinct primes s Dn = divisors of n s Quintuple (Dn, lcm, gcd , 1, n) s Example n = 30 - ({1, 2, 3, 5, 6, 10, 15, 30}, lcm, gcd, 1, 30) (c) Giovanni De Micheli 6

The don’t care conditions u We do not care about the value of a function u Related to the environment s Input patterns that never occur s Input patterns such that some output is never observed u Very important for synthesis and optimization (c) Giovanni De Micheli 7

Definitions u Scalar function: s ON-set t s OFF-set t s Subset of the domain such that f is true Subset of the domain such that f is false DC-set t Subset of the domain such that f is a don’t care u Multiple-output function: s ON, OFF, DC-sets defined for each component (c) Giovanni De Micheli 8

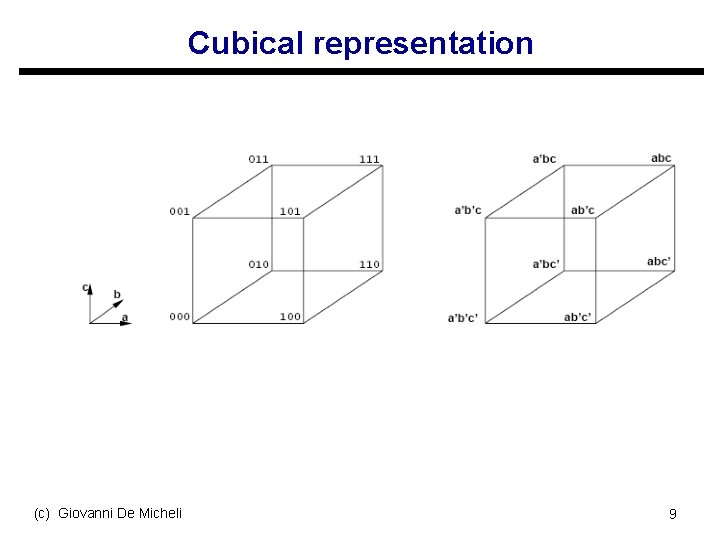
Cubical representation (c) Giovanni De Micheli 9

Definitions u Boolean variables u Boolean literals: s Variables and their complement u Product or cube: s Product of literals u Implicant: s Product implying a value of the function (usually 1) s Hypercube in the Boolean space u Minterm: s Product of all input variables implying a value of the function (usually 1) s Vertex in the Boolean space (c) Giovanni De Micheli 10

Tabular representations u Truth table s List of all minterms of a function u Implicant table or cover s List of implicants sufficient to define a function u Note: s Implicant tables are smaller in size as compared to truth tables (c) Giovanni De Micheli 11

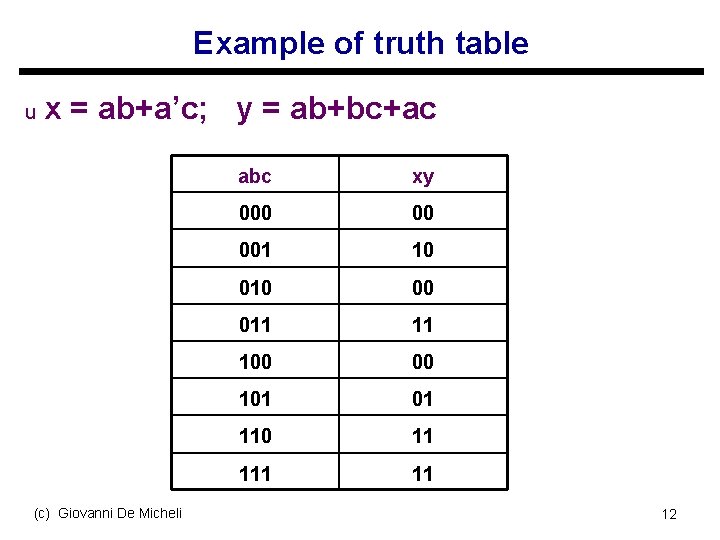
Example of truth table u x = ab+a’c; y = ab+bc+ac (c) Giovanni De Micheli abc xy 000 00 001 10 00 011 11 100 00 101 01 110 11 11 12

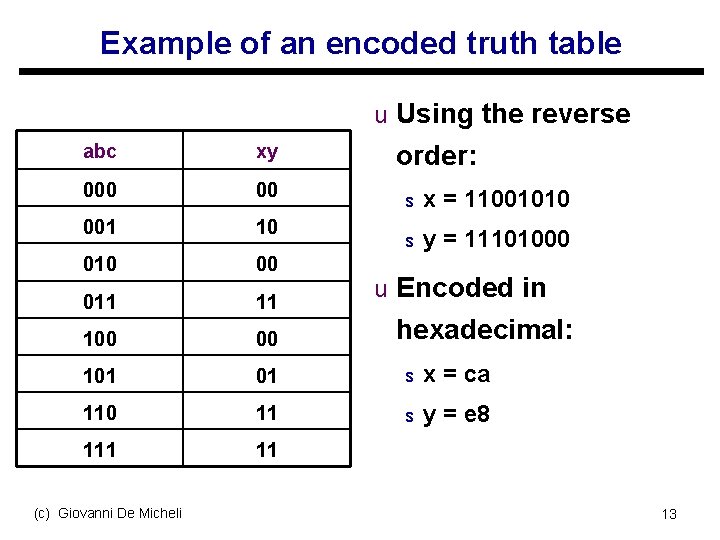
Example of an encoded truth table u Using the reverse order: abc xy 000 00 001 10 00 011 11 100 00 101 01 s x = ca 110 11 s y = e 8 111 11 (c) Giovanni De Micheli s x = 11001010 s y = 11101000 u Encoded in hexadecimal: 13

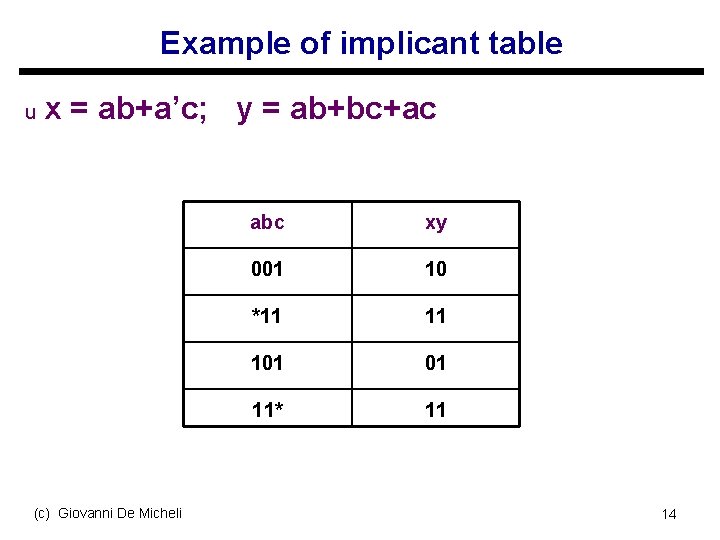
Example of implicant table u x = ab+a’c; y = ab+bc+ac (c) Giovanni De Micheli abc xy 001 10 *11 11 101 01 11* 11 14

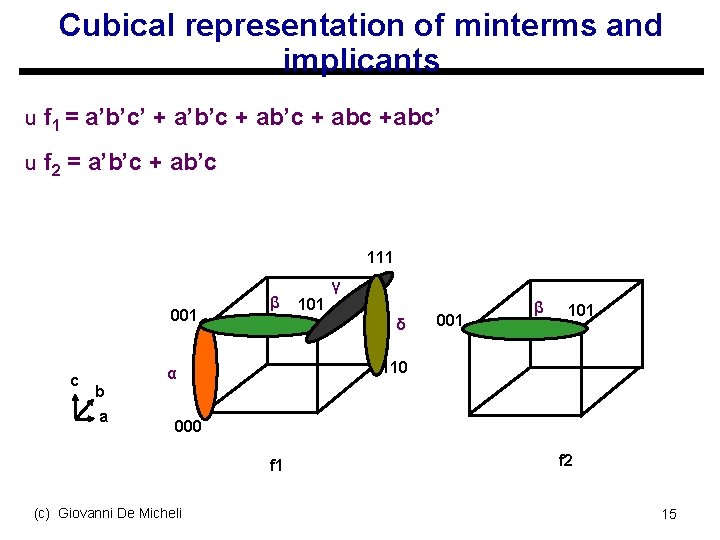
Cubical representation of minterms and implicants u f 1 = a’b’c’ + a’b’c + abc +abc’ u f 2 = a’b’c + ab’c 111 001 c β γ 101 δ 001 β 101 110 α b a 000 f 1 (c) Giovanni De Micheli f 2 15

Representations u Visual representations s Cubical notation s Karnaugh maps u Computer-oriented representations s Matrices t t s Sparse Various encoding Binary-decision diagrams t Address sparsity and efficiency (c) Giovanni De Micheli 16

Module 2 u Objectives s Two-level logic optimization s Motivation s Models s Exact algorithms for logic optimization (c) Giovanni De Micheli 17

Two-level logic optimization motivation u Reduce size of the representation u Direct implementation s PLAs reduce size and delay u Other implementation styles s Reduce amount of information s Simplify local functions and connections (c) Giovanni De Micheli 18

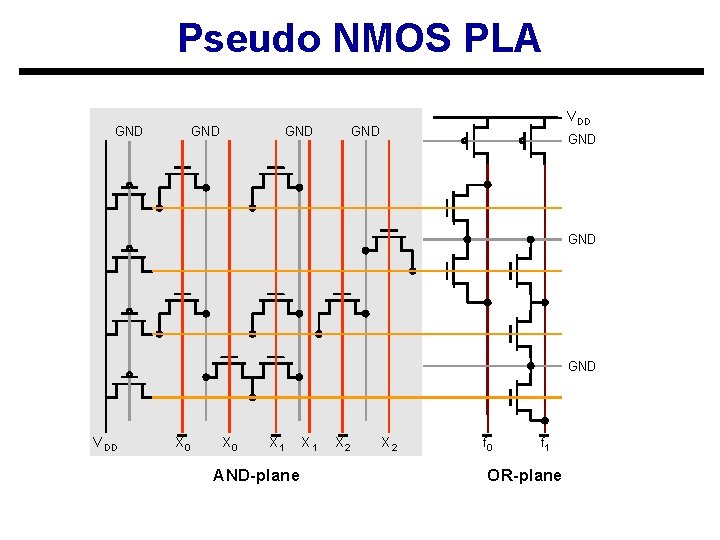
Programmable logic arrays u Macro-cells with rectangular structure s Implement any multi-output function u Programmable s Old technology using fuses s Grandfather of FPGAs u Programmed s Layout generated by module generators s Fairly popular in the seventies/eighties u Advantages s Simple, predictable timing u Disadvantages s Less flexible than cell-based realization s Dynamic operation in CMOS u Open issue s Will PLA structures be useful with new nanotechnologies? (c) Giovanni De Micheli 19

Pseudo NMOS PLA GND GND V DD X 0 X 1 AND-plane X 1 X 2 f 0 f 1 OR-plane

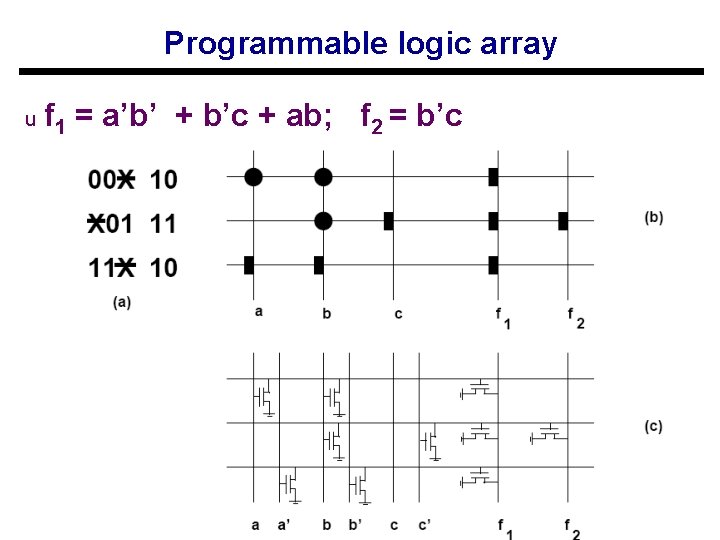
Programmable logic array u f 1 = a’b’ + b’c + ab; f 2 = b’c (c) Giovanni De Micheli 21

Two-level minimization u Assumptions s Primary goal is to reduce the number of implicants s All implicants have the same cost s Secondary goal is to reduce the number of literals u Rationale s Implicants correspond to PLA rows s Literals correspond to transistors (c) Giovanni De Micheli 22

Definitions u Minimum cover s Cover of a function with minimum number of implicants s Global optimum u Minimal cover or irredundant cover s Cover of the function that is not a proper superset of another cover s No implicant can be dropped s Local optimum u Minimal w. r. to 1 -implicant containment s No implicant contained by another one s Weak local optimum (c) Giovanni De Micheli 23

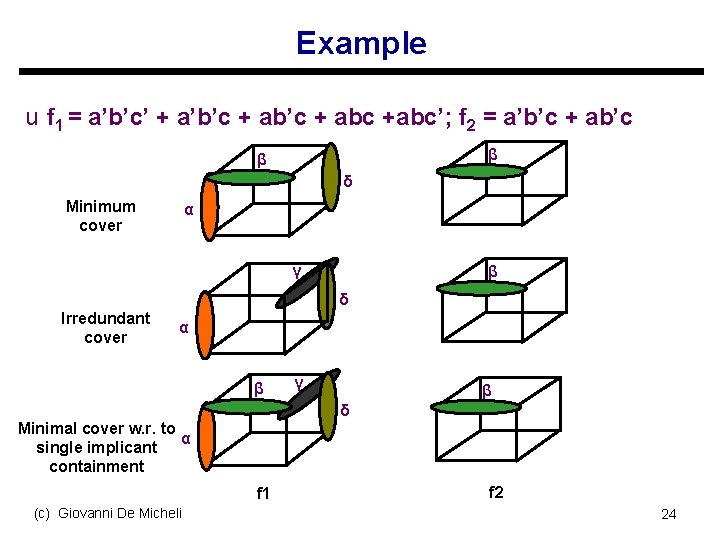
Example u f 1 = a’b’c’ + a’b’c + abc +abc’; f 2 = a’b’c + ab’c β β δ Minimum cover α γ β δ Irredundant cover α β γ β δ Minimal cover w. r. to α single implicant containment f 1 (c) Giovanni De Micheli f 2 24

Definitions u Prime implicant s Implicant not contained by any other implicant u Prime cover s Cover of prime implicants u Essential prime implicant s There exist some minterm covered only by that prime implicant s Needs to be included in the cover (c) Giovanni De Micheli 25

Two-level logic minimization u Exact methods s Compute minimum cover s Often difficult/impossible for large functions s Based on Quine-Mc. Cluskey method u Heuristic methods s Compute minimal covers (possibly minimum) s Large variety of methods and programs t MINI, PRESTO, ESPRESSO (c) Giovanni De Micheli 26

Exact logic minimization u Quine’s theorem: s There is a minimum cover that is prime u Consequence s Search for minimum cover can be restricted to prime implicants u Quine-Mc. Cluskey method s Compute prime implicants s Determine minimum cover (c) Giovanni De Micheli 27

Prime implicant table u Rows: minterms u Columns: prime implicants u Exponential size s 2 n minterms s Up to 3 n / n prime implicants u Remarks s Some functions have much fewer primes s Minterms can be grouped together s Implicit methods for implicant enumeration (c) Giovanni De Micheli 28

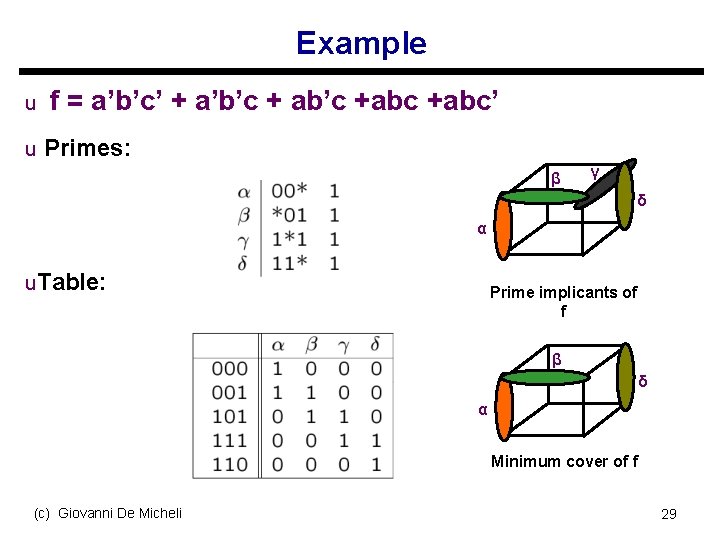
Example u f = a’b’c’ + a’b’c + ab’c +abc’ u Primes: β γ δ α u. Table: Prime implicants of f β δ α Minimum cover of f (c) Giovanni De Micheli 29

Minimum cover early methods u Reduce table s Iteratively identify essentials, save them in the cover. Remove covered minterms u Petrick’s method s Write covering clauses in pos form s Multiply out pos form into sop form s Select cube of minimum size u Remark s Multiplying out clauses has exponential cost (c) Giovanni De Micheli 30

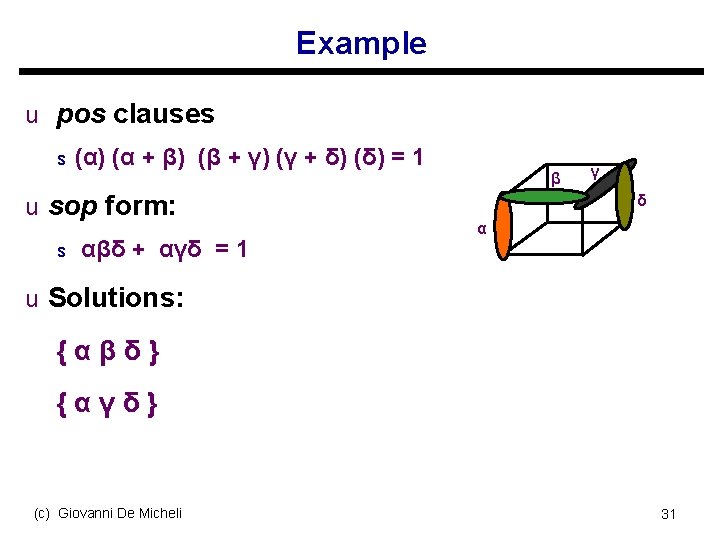
Example u pos clauses s (α) (α + β) (β + γ) (γ + δ) (δ) = 1 u sop form: s αβδ + αγδ = 1 β γ δ α u Solutions: {αβδ} {αγδ} (c) Giovanni De Micheli 31

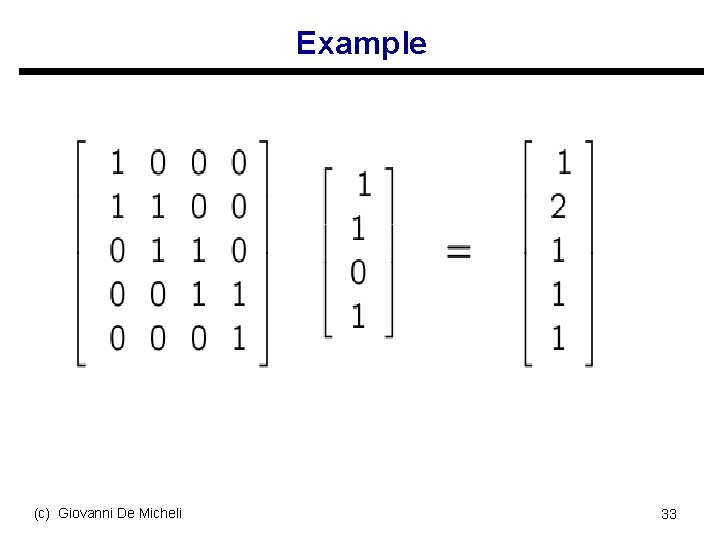
Matrix representation u View table as Boolean matrix: A u Selection Boolean vector for primes: x u Determine x such that s Ax≥ 1 s Select enough columns to cover all rows u Minimize norm (1 count) of x (c) Giovanni De Micheli 32

Example (c) Giovanni De Micheli 33

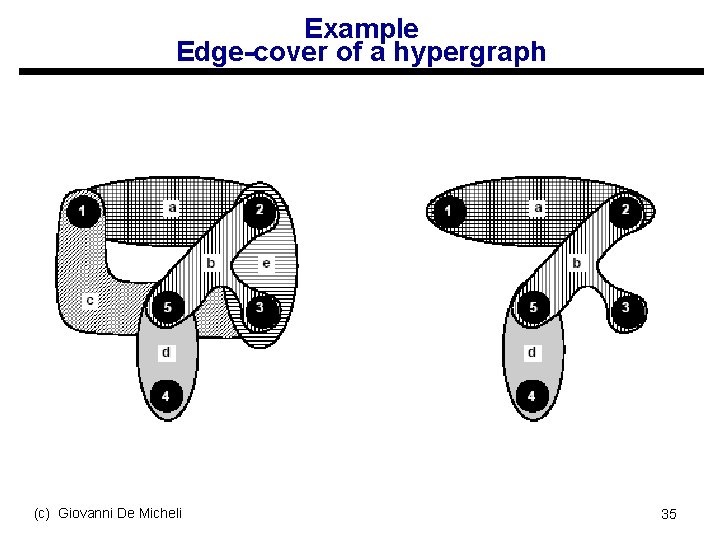
Covering problem u Set covering problem: s A set S -- minterm set s A collection C of subsets (implicant set) s Select fewest elements of C to cover S u Computationally intractable problem u Exact solution method s Branch and bound algorithm u Several heuristic approximation methods (c) Giovanni De Micheli 34

Example Edge-cover of a hypergraph (c) Giovanni De Micheli 35

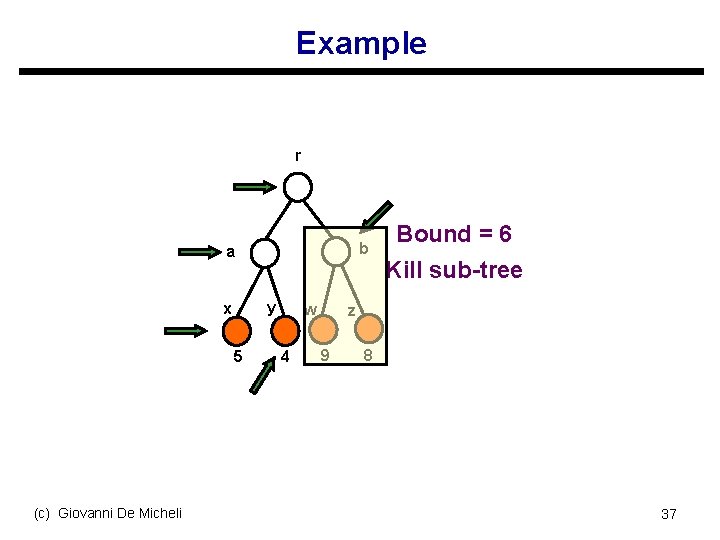
Branch and bound algorithm u Tree search in the solution space s Potentially exponential u Use bounding function: s If the lower bound on the solution cost that can be derived from a set of future choices exceeds the cost of the best solution seen so far, then kill the search s Bounding function should be fast to evaluate and accurate u Good pruning may expedite the search (c) Giovanni De Micheli 36

Example r b a y x 5 (c) Giovanni De Micheli w 4 Bound = 6 Kill sub-tree z 9 8 37

Branch and bound for logic minimization Reduction strategies u Use matrix formulation of the problem u Partitioning: s If A is block diagonal: t Solve covering problems for the corresponding blocks u Essentials s Column incident to one (or more) rows with single 1 t t Select column Remove covered row(s) from table (c) Giovanni De Micheli 38

Branch and bound for logic minimization Reduction strategies u Column (implicant) dominance: s If aki ≥ akj for all k t s Remove column j (dominated) Dominated implicant ( j ) has its minterms already covered by dominant implicant ( i ) u Row (minterm) dominance: s If aik ≥ ajk for all k t s Remove row i (dominant) When an implicant covers the dominated minterm, it also covers the dominant one (c) Giovanni De Micheli 39

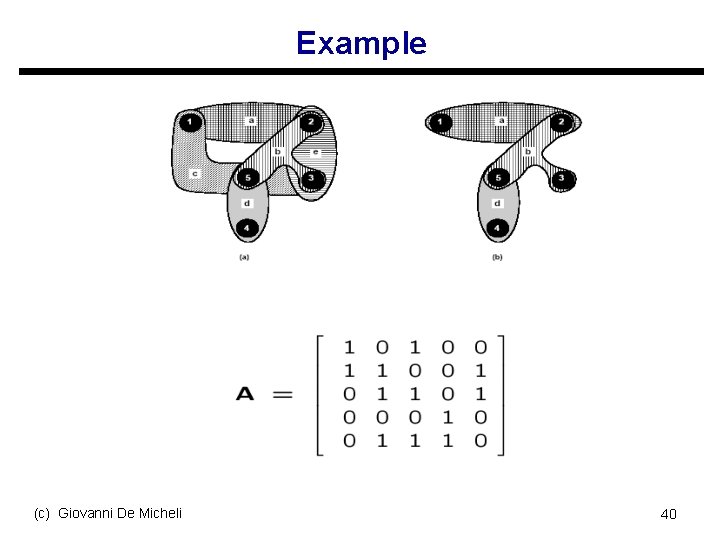
Example (c) Giovanni De Micheli 40

Example u. Fifth row is dominant u. Fourth column is essential u. Fifth column is dominated u. Matrix after reductions: (c) Giovanni De Micheli 41

Branch and bound covering algorithm EXACT_COVER(A, x, b) { Reduce matrix A and update corresponding x; if (current_estimate ≥ |b|) return (b); if (A has no rows) return(x); select a branching column c; xc = 1; Ã = A after deleting c and rows incident to it; x~ = EXACT_COVER(Ã, x, b); if ( | x~| < |b| ) b = x ~; xc = 0; Ã = A after deleting c; x~ = EXACT_COVER(Ã, x, b); if ( | x~| < |b| ) b = x ~; return(b); } (c) Giovanni De Micheli 42

Bounding function u Estimate lower bound on covers that can be derived from current solution vector x u The sum of the 1 s in x, plus bound of cover for local A s Independent set of rows t t No 1 in the same column Require independent implicants to cover s Construct graph to show pairwise independence s Find clique number t s Size of the largest clique Approximation (lower) is acceptable (c) Giovanni De Micheli 43

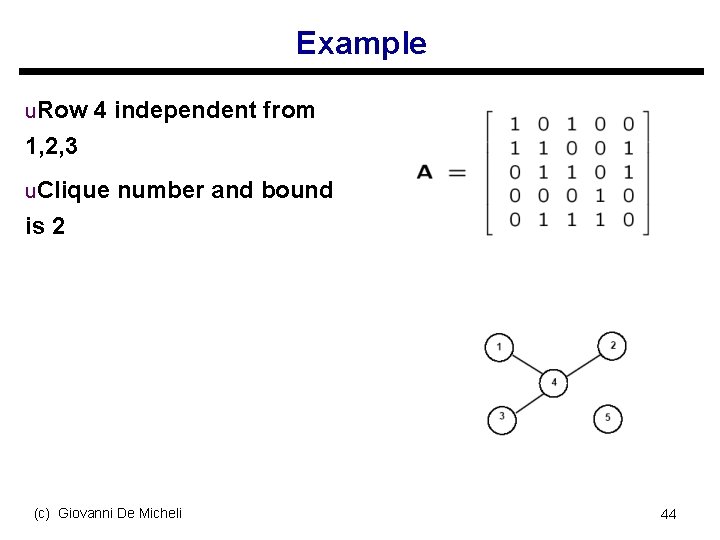
Example u. Row 4 independent from 1, 2, 3 u. Clique number and bound is 2 (c) Giovanni De Micheli 44

Example u. There are no independent rows s Clique number is 1 (one vertex) s Bound is 1+1= 2 t A = 1 0 1 1 1 0 0 1 1 Because of the essential already selected (c) Giovanni De Micheli 45

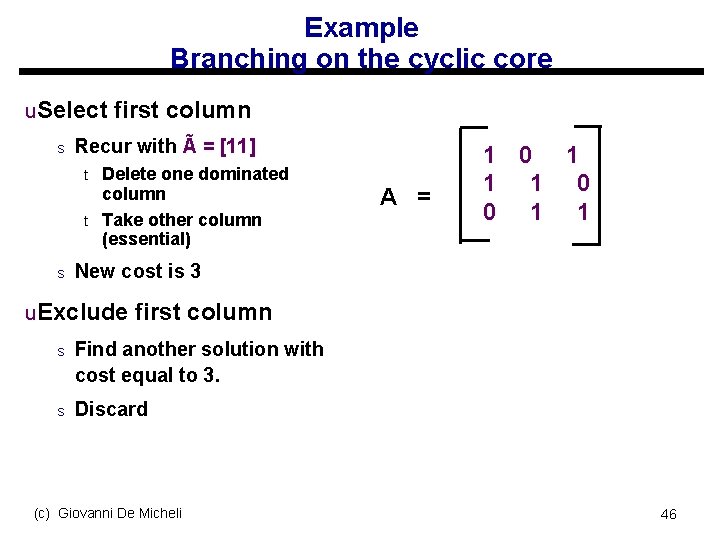
Example Branching on the cyclic core u. Select first column s Recur with à = [11] t t s Delete one dominated column Take other column (essential) A = 1 0 1 1 1 0 0 1 1 New cost is 3 u. Exclude first column s Find another solution with cost equal to 3. s Discard (c) Giovanni De Micheli 46

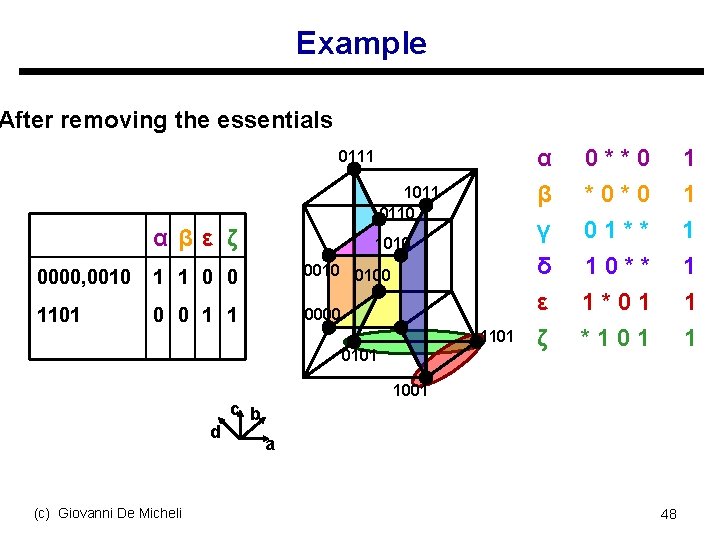
Espresso-exact u Exact 2 -level logic minimizer u Exploits iterative reduction and branch and bound algorithm on cyclic core u Compact implicant table s Rows represent groups of minterms covered by the same implicants u Very efficient s Solves most benchmarks (c) Giovanni De Micheli 47

Example After removing the essentials 0111 1011 0110 αβ ε ζ 1010 0000, 0010 1 1 0 0 0010 0100 1101 0 0 1 1 0000 1101 0101 d (c) Giovanni De Micheli α β γ δ ε ζ 0**0 *0*0 01** 10** 1*01 *101 1 1 1 1001 c b a 48

Exact two-level minimization u There are two main difficulties: s Storage of the implicant table s Solving the cyclic core u Implicit representation of prime implicants s Methods based on binary decision diagrams s Avoid explicit tabulation u Recent methods make 2 -level optimization solve exactly almost all benchmarks s Heuristic optimization is just used to achieve solutions faster (c) Giovanni De Micheli 49

Module 3 u Boolean Relations s Motivation of using relations s Optimization of realization of Boolean relation s Comparisons to two-level optimization (c) Giovanni De Micheli 50

Boolean relations u Generalization of Boolean functions u More than one output pattern may correspond to an input pattern s Multiple-choice specifications s Model inner blocks of multi-level circuits u Degrees of freedom in finding an implementation s More general than don’t care conditions u Problem: Given a Boolean relation, find a minimum cover of a Giovanni De Micheli compatible Boolean function that can implement the 51 s (c)

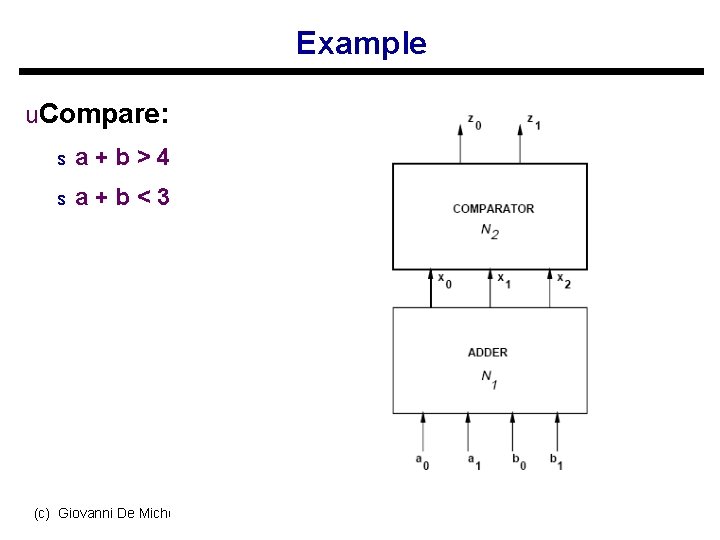
Example u. Compare: s a+b>4? s a+b<3? (c) Giovanni De Micheli 52

Example Note that output 111 cannot be a+b but can considered as a don’t c (c) Giovanni De Micheli 53

Example u. Circuit is no longer an adder (c) Giovanni De Micheli 54

Minimization of Boolean relations u Since there are many possible output values (for any input), there are many logic functions implementing the relation s Compatible functions u Problem s Find a minimum compatible function u Do not enumerate all compatible functions s Compute the primes of the compatible functions t s C-primes Derive a logic cover from the c-primes (c) Giovanni De Micheli 55

Binate covering u Covering problem is more complex s As compared to minimizing logic functions. u In classic Boolean minimization we just need enough implicants to cover the minterm s Covering clause is unate in all variables s Any additional implicant does not hurt u In Boolean relation optimization, we need to pick implicants to realize a compatible function s Some implicants cannot be taken together s Covering clause is binate (implicant mutual exclusion) s Non-compact Boolean space (c) Giovanni De Micheli 56

Solving binate covering u Binate cover can be solved with branch and bound s In practice much more difficult to solve, because it is harder to bound effectively u Binate cover can be reduced to min-cost SAT solvers can be used u Binate cover can be also modeled by BDDs u Several approximation algorithms for binate cover (c) Giovanni De Micheli 57

Summary: Boolean Relations u Generalization of Boolean functions s More degrees of freedom than don’t care sets u Useful to represent multiple choice u Useful to model internals of logic networks u Elegant formalism, but computationally- intensive solution method (c) Giovanni De Micheli 58