Scheduling Giovanni De Micheli Integrated Systems Centre EPF

Scheduling Giovanni De Micheli Integrated Systems Centre EPF Lausanne This presentation can be used for non-commercial purposes as long as this note and the copyright footers are not removed © Giovanni De Micheli – All rights reserved

Scheduling u Circuit model: s Sequencing graph s Cycle-time is given s Operation delays expressed in cycles u Scheduling: s Determine the start times for the operations s Satisfying all the sequencing (timing and resource) constraint u Goal: s Determine area/latency trade-off (c) Giovanni De Micheli 2

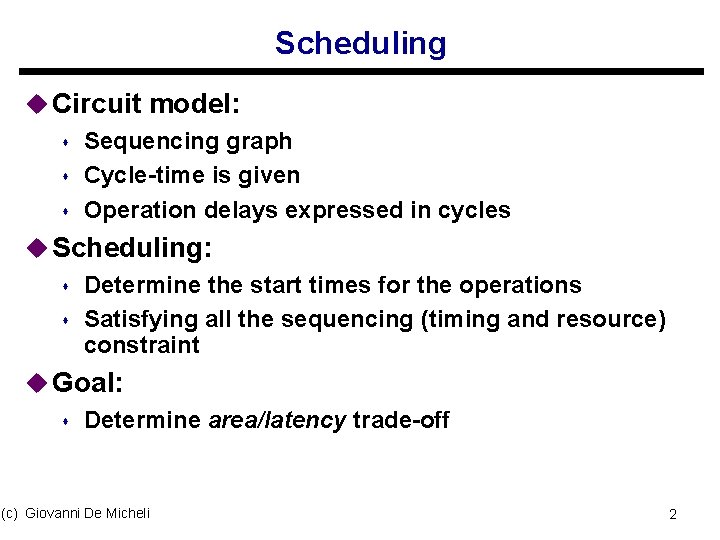
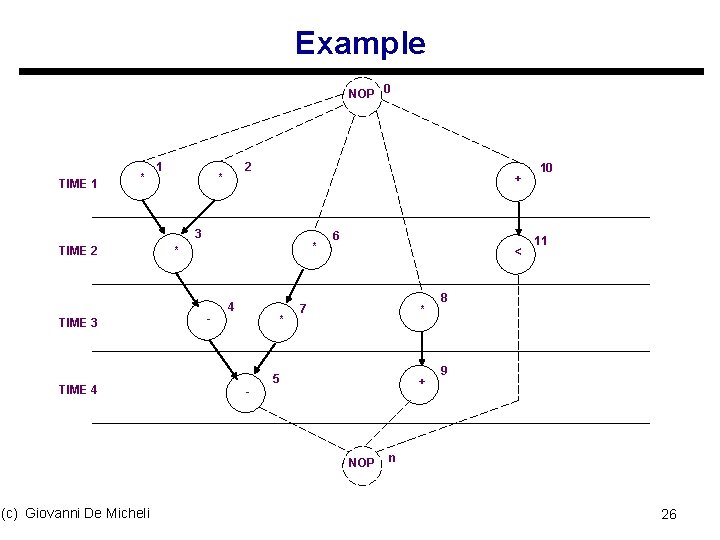
Example NOP 0 * 1 2 * * 3 * * - 6 * 7 + 8 + 9 < 10 11 4 - 5 NOP n NOP 0 TIME 1 TIME 2 TIME 3 TIME 4 (c) Giovanni De Micheli * 1 2 * * 3 * * - 6 * 7 + 8 9 + < 10 11 4 - 5 NOP n 3

Taxonomy u Unconstrained scheduling u Scheduling with timing constraints: s Latency s Detailed timing constraints u Scheduling with resource constraints u Related problems: s Chaining s Synchronization s Pipeline scheduling (c) Giovanni De Micheli 4

Simplest method u. All operations have bounded delays u. All delays are in cycles: s Cycle-time is given u. No constraints – no bounds on area u. Goal: s Minimize latency (c) Giovanni De Micheli 5

Minimum-latency unconstrained scheduling problem u. Given a set of ops V with integer delays D and a partial order on the operations E: u. Find an integer labeling of the operations φ : V →Z+ such that: ti ≥ tj + d j A ti = φ( vi ), i, j s. t. ( vj , vi ) є E and tn is minimum (c) Giovanni De Micheli 6

ASAP scheduling algorithm ASAP ( Gs(V, E) ) { Schedule v 0 by setting t 0 = 1; repeat { Select a vertex vi whose predecessors are all scheduled; Schedule vi by setting ti = max tj + dj ; } j: (vj, vi) є E until (vn is scheduled); return (t ); } (c) Giovanni De Micheli 7

Example NOP 0 TIME 1 * 1 2 * * 3 TIME 2 TIME 3 TIME 4 * * - 6 7 * + 8 9 + < 10 11 4 - 5 NOP n (c) Giovanni De Micheli 8

ALAP scheduling algorithm ALAP ( Gs(V, E), λ ) { Schedule vn by setting tn = λ + 1; repeat { Select a vertex vi whose successors are all scheduled; Schedule vi by setting ti = min tj - di; } j: (vi, vj) є E until (v 0 is scheduled); return (t); } (c) Giovanni De Micheli 9

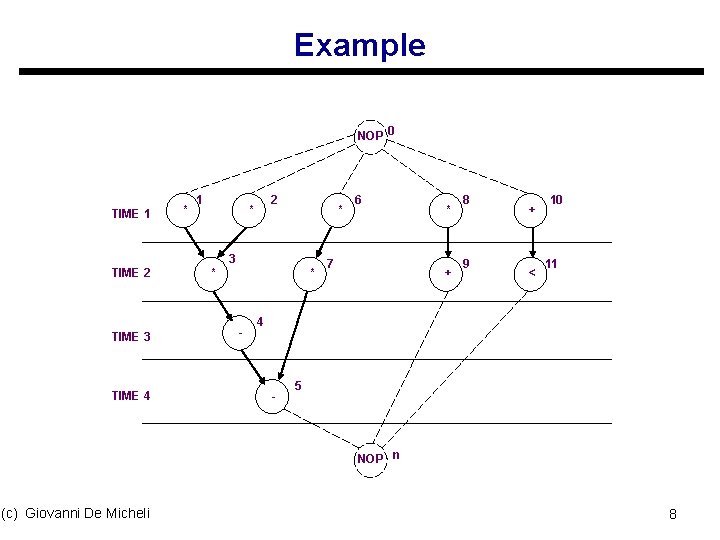
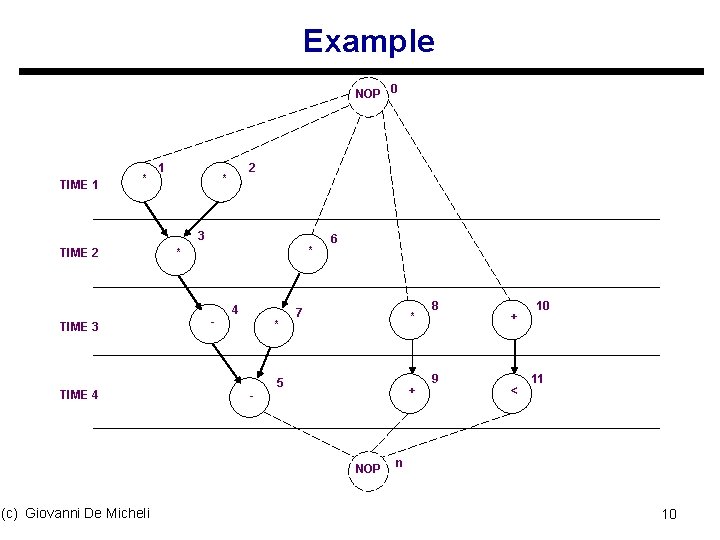
Example NOP 0 TIME 1 * 1 2 * 3 TIME 2 TIME 3 TIME 4 * * - 4 * - 6 7 * 5 + NOP (c) Giovanni De Micheli 8 9 + < 10 11 n 10

Remarks u ALAP solves a latency-constrained problem u Latency bound can be set to latency computed by ASAP algorithm u Mobility: s Defined for each operation s Difference between ALAP and ASAP schedule u Slack on the start time (c) Giovanni De Micheli 11

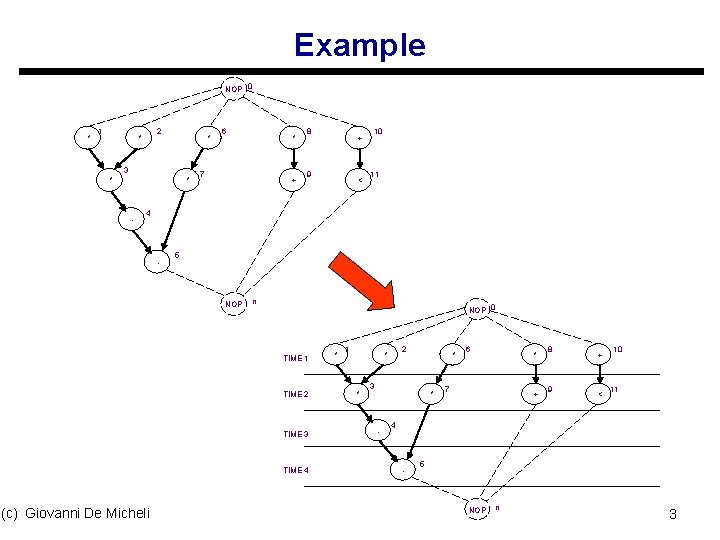
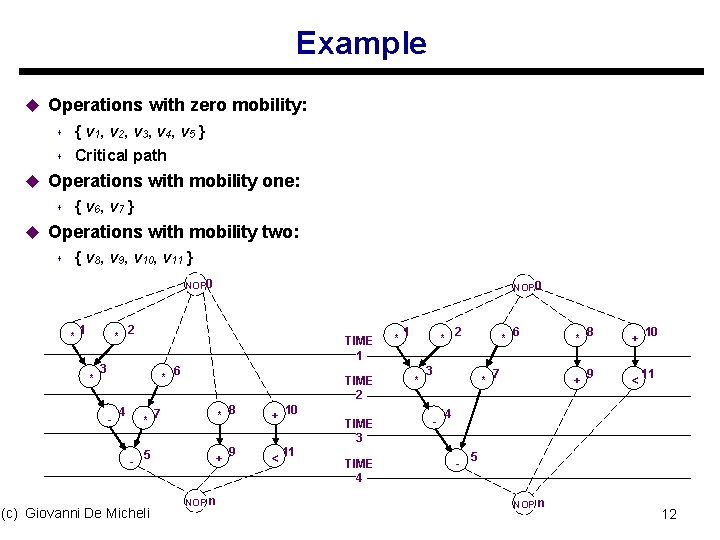
Example u Operations with zero mobility: s s { v 1, v 2, v 3, v 4, v 5 } Critical path u Operations with mobility one: s { v 6 , v 7 } u Operations with mobility two: s { v 8, v 9, v 10, v 11 } NOP 0 * 1 2 * * TIME 1 3 * - NOP 0 4 * - 5 (c) Giovanni De Micheli 6 TIME 2 7 * + NOP n 8 9 + < 10 TIME 3 11 TIME 4 * 1 2 * * * 3 * - 6 7 * + 8 9 + < 10 11 4 - 5 NOP n 12

Scheduling under detailed timing constraints u. Motivation: s Interface design s Control over operation start time u. Constraints: s Upper/lower bounds on start-time difference of any operation pair u. Feasibility of a solution (c) Giovanni De Micheli 13

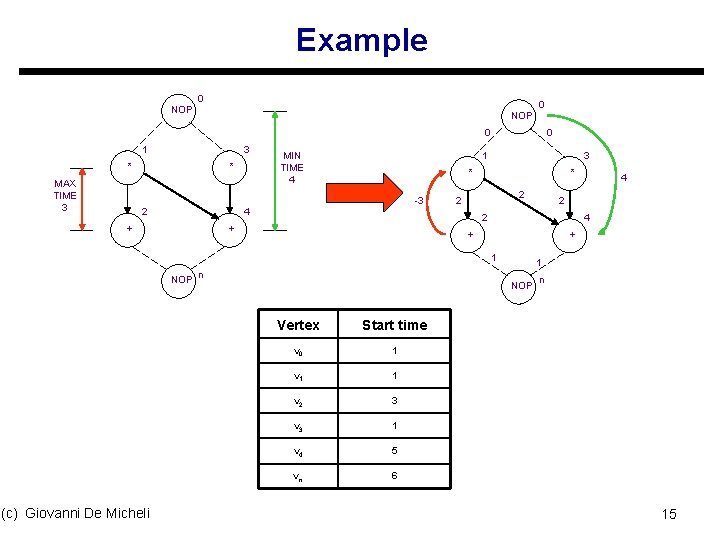
Constraint graph model u Start from sequencing graph s Model delays as weights on edges u Add forward edges for minimum constraints: s Edge ( vi , vj ) with weight lij → tj ≥ ti + lij u Add backward edges for maximum constraints: s That is, for constraint from vi to vj add backward edge ( vj , vi ) with weight: -uij t because tj ≤ ti + uij → ti ≥ tj - uij (c) Giovanni De Micheli 14

Example 0 0 NOP 0 1 3 * MAX TIME 3 * MIN TIME 4 1 * 2 2 4 + 3 * -3 2 0 4 + + 1 NOP (c) Giovanni De Micheli 2 2 + 1 n NOP Vertex Start time v 0 1 v 1 1 v 2 3 v 3 1 v 4 5 vn 6 4 n 15

Methods for scheduling under detailed timing constraints u Assumption: s All delays are fixed and known u Set of linear inequalities u Longest path problem u Algorithms: s Bellman-Ford, Liao-Wong u Extensions: s Unbounded delays, relative scheduling (c) Giovanni De Micheli 16

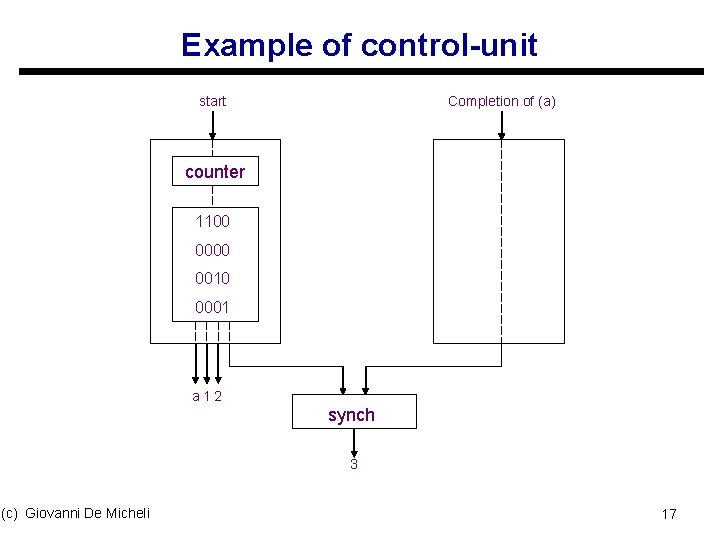
Example of control-unit start Completion of (a) counter 1100 0010 0001 a 12 synch 3 (c) Giovanni De Micheli 17

Scheduling under resource constraints u Classical scheduling problem: s Fix area bound – minimize latency u The amount of available resources affects the achievable latency u Dual problem: s Fix latency bound – minimize resources u Assumption: s All delays bounded and known (c) Giovanni De Micheli 18

Minimum latency resource-constrained scheduling problem u Given a set of ops V with integer delays D, a partial order on the operations E, and upper bounds { ak; k = 1, 2, …, nres } on resource usage: u Find an integer labeling of the operation φ: V → z+ such that : ti = φ( vi ), ti ≥ tj + d j for all i, j s. t. (vj, vi) є E, | {vi |T(vi) = k and ti ≤ l < tj + dj } | ≤ ak 1, 2, …, nres (c) Giovanni De Micheli for all types k = and steps l 19

Scheduling under resource constraints u. Intractable problem u. Algorithms: s Exact: t t s Integer linear program Hu (restrictive assumptions) Approximate : t t List scheduling Force-directed scheduling (c) Giovanni De Micheli 20

ILP formulation u. Binary decision variables: X = { xil, i = 1, 2, …. n; l = 1, 2, …, λ + 1} xil is TRUE only when operation vi starts in step l of the schedule ( i. e. l = ti ) λ is an upper bound on latency u. Start time of operation vi : (c) Giovanni De Micheli Σl l. xil 21

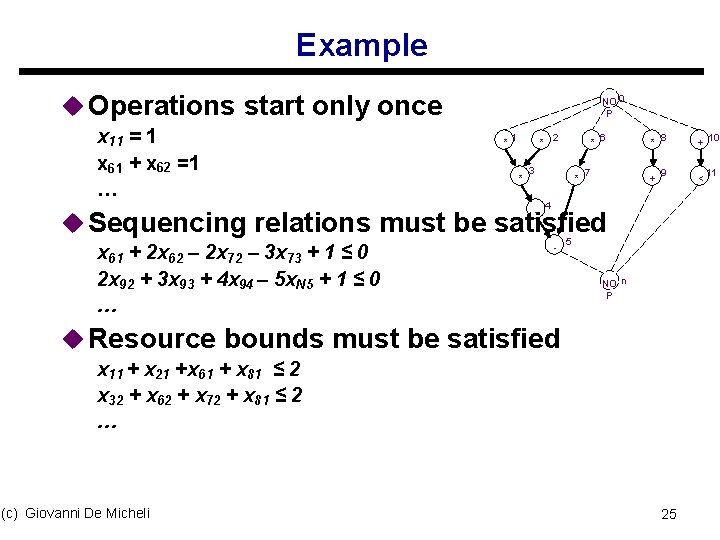
ILP formulation constraints u Operations start only once Σ xil = 1 i = 1, 2, …, n u Sequencing relations must be satisfied ti ≥ t j + d j ti - tj - dj ≥ 0 for all (vj, vi) є E Σ l • xil – Σ l • xjl – dj ≥ 0 for all (vj, vi) є E u Resource bounds must be satisfied Simple case (unit delay) Σl xil ≤ ak k = 1, 2, …nres ; for all l i: T(vi)=k (c) Giovanni De Micheli 22

ILP Formulation min ||t|| such that Σ xij = 1 j Σ l • xil - Σ l • xjl - dj ≥ 0 l l Σ i: T(vi)=k (c) Giovanni De Micheli Σl xim ≤ ak i = 1, 2, …, n i, j = 1, 2, …, n, (vj, vi) є E k = 1, 2, …, nres ; l = 0, 1, …, tn m=l-di+1 23

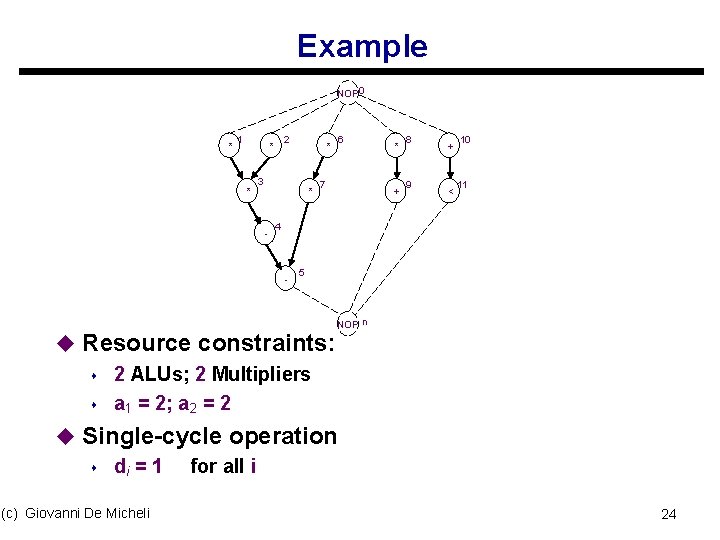
Example NOP 0 * 1 2 * * * 3 * - 6 7 * + 8 9 + < 10 11 4 - 5 u Resource constraints: s 2 ALUs; 2 Multipliers s a 1 = 2; a 2 = 2 NOP n u Single-cycle operation s di = 1 for all i (c) Giovanni De Micheli 24

Example u Operations start only once x 11 = 1 x 61 + x 62 =1 … NO 0 P * 1 2 * * * 3 * - 6 7 * + 8 9 4 u Sequencing relations must be satisfied x 61 + 2 x 62 – 2 x 72 – 3 x 73 + 1 ≤ 0 2 x 92 + 3 x 93 + 4 x 94 – 5 x. N 5 + 1 ≤ 0 … - 5 NO n P u Resource bounds must be satisfied x 11 + x 21 +x 61 + x 81 ≤ 2 x 32 + x 62 + x 72 + x 81 ≤ 2 … (c) Giovanni De Micheli 25 + < 10 11

Example NOP 0 TIME 1 * 1 2 * + 3 TIME 2 TIME 3 TIME 4 * * - 4 * - 6 < 7 * 5 + NOP (c) Giovanni De Micheli 10 11 8 9 n 26

Dual ILP formulation u. Minimize resource usage under latency constraint u. Additional constraint: s Latency bound must be satisfied s Σl l xnl ≤ λ + 1 u. Resource usage is unknown in the constraints u. Resource usage is the objective to minimize (c) Giovanni De Micheli 27

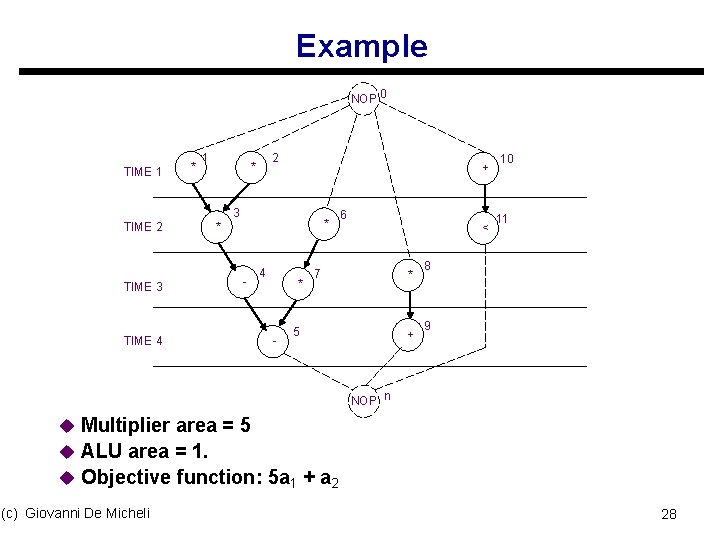
Example NOP 0 TIME 1 * 1 2 * + 3 TIME 2 TIME 3 * * - TIME 4 4 * - 6 < 7 * 5 + 10 11 8 9 NOP n u Multiplier area = 5 u ALU area = 1. u Objective function: 5 a 1 + a 2 (c) Giovanni De Micheli 28

ILP Solution u. Use standard ILP packages u. Transform into LP problem u. Advantages: s Exact method s Other constraints can be incorporated u. Disadvantages: s Works well up to few thousand variables (c) Giovanni De Micheli 29

Hu’s algorithm u. Assumptions: s Graph is a forest s All operations have unit delay s All operations have the same type u. Algorithm: s Greedy strategy s Exact solution (c) Giovanni De Micheli 30

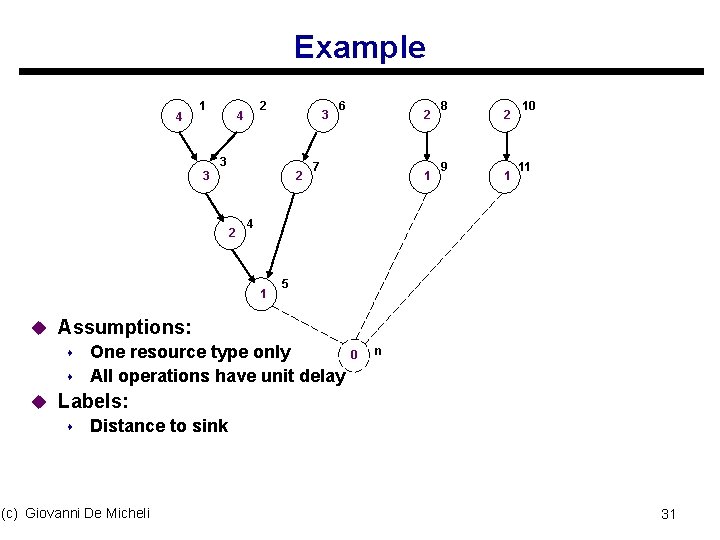
Example 4 1 2 4 3 3 3 2 2 6 7 1 8 9 2 1 10 11 4 1 5 u Assumptions: s One resource type only s All operations have unit delay u Labels: s Distance to sink (c) Giovanni De Micheli 2 0 n 31

Algorithm Hu’s schedule with ā resources u Label operations with distance to sink u Set step l = 1 u Repeat until all ops are scheduled: s Select s ≤ ā resources with t t s s All predecessors scheduled Maximal labels Schedule the s operations at step l Increment step l = l + 1 (c) Giovanni De Micheli 32

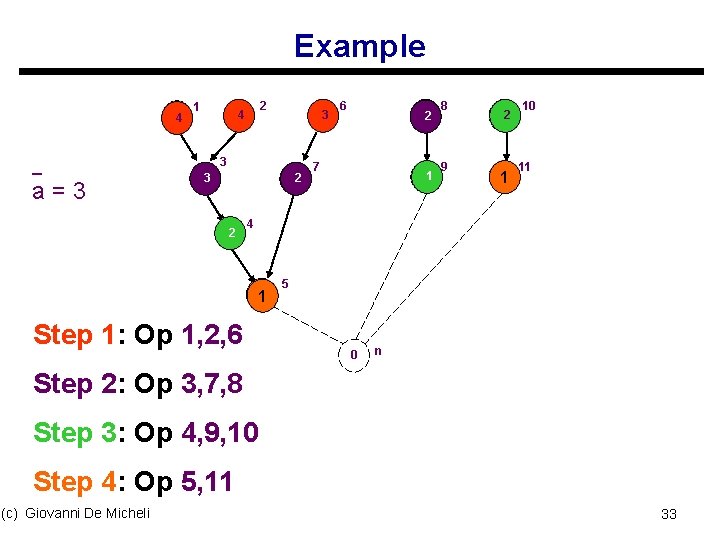
Example 4 _ a=3 1 2 4 3 3 3 2 2 6 2 7 11 8 9 2 11 10 11 4 1 1 Step 1: Op 1, 2, 6 5 0 n Step 2: Op 3, 7, 8 Step 3: Op 4, 9, 10 Step 4: Op 5, 11 (c) Giovanni De Micheli 33

Exactness of Hu’s algorithm u. Definitions: s Label of vertex vi is called αi s Maximal label is called α s Number of vertices with label b is called p(b) s Latency is called λ s A lower bound on the number of resources to complete a schedule with latency λ is called ā (c) Giovanni De Micheli 34

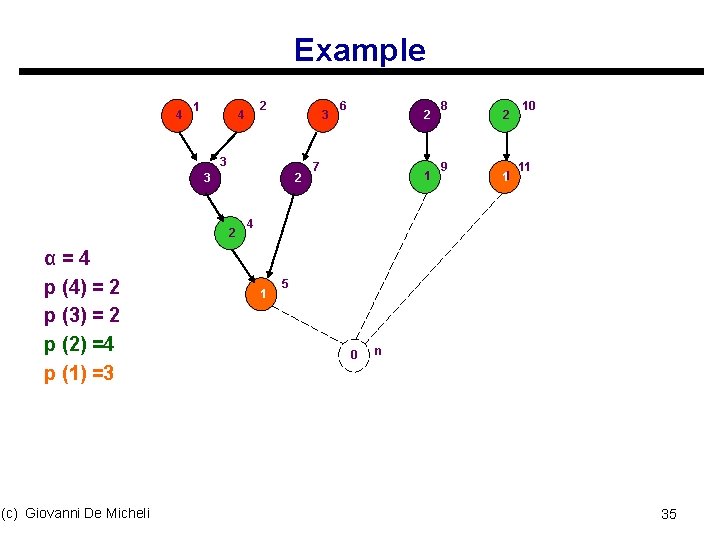
Example 4 1 2 4 3 3 3 2 2 α=4 p (4) = 2 p (3) = 2 p (2) =4 p (1) =3 (c) Giovanni De Micheli 6 2 7 1 8 9 2 1 10 11 4 1 1 5 0 n 35

Exactness of Hu’s algorithm γ u Theorem 1: s Given a dag with operations of the same type γ ┐ s ā = max ┌ Σj=1 p( α + 1 – j) γ+λ-α s s ā is a lower bound on the number of resources to complete a schedule with latency λ γ is a positive integer u Theorem 2: s Hu’s algorithm applied to a tree with ā unit-cycle resources achieves latency λ u Corollary: s Since ā is a lower bound on the number of resources for achieving λ, then λ is minimum (c) Giovanni De Micheli 36

List scheduling algorithms u Heuristic method for: s Min latency subject to resource bound s Min resource subject to latency bound u Greedy strategy (like Hu’s) u General graphs (unlike Hu’s) u Priority list heuristics s Longest path to sink s Longest path to timing constraint (c) Giovanni De Micheli 37

List scheduling algorithm for minimum latency LIST_L( G(V, E), a) { l = 1; repeat { for each resource type k = 1, 2, …, nres { Determine ready operations Ul, k; Determine unfinished operations Tl, k; Select Sk Ul, k vertices, s. t. |Sk| + |Tl, k| ≤ ak; Schedule the Sk operations at step l; } l = l + 1; } until (vn is scheduled) ; return (t); } (c) Giovanni De Micheli 38

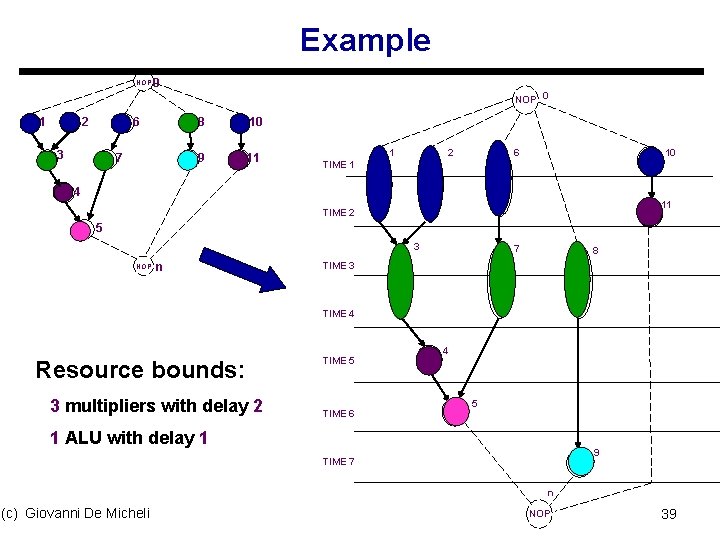
Example NOP 0 *1 * 2 * 3 * 6 * 7 * 8 + 10 +9 < 11 1 TIME 1 2 * 6 + * * - 4 TIME 2 < 10 11 - 5 3 NOP n TIME 3 7 * 8 * * TIME 4 Resource bounds: 3 multipliers with delay 2 TIME 5 TIME 6 - 4 - 5 1 ALU with delay 1 TIME 7 + 9 n (c) Giovanni De Micheli NOP 39

List scheduling algorithm for minimum resource usage LIST_R( G(V, E), λ) { a = 1; Compute the latest possible start times t. L by ALAP ( G(V, E), λ); if (t 0 < 0) return (Ø); L l = 1; repeat { for each resource type k = 1, 2, …, nres { Determine ready operations Ul, k; L Compute the slacks { si = ti – l for all vi є Ulk}; Schedule the candidate operations with zero slack and update a; Schedule the candidate operations not needing additional resources; } l = l + 1; } until (vn is scheduled) ; return (t, a); } (c) Giovanni De Micheli 40

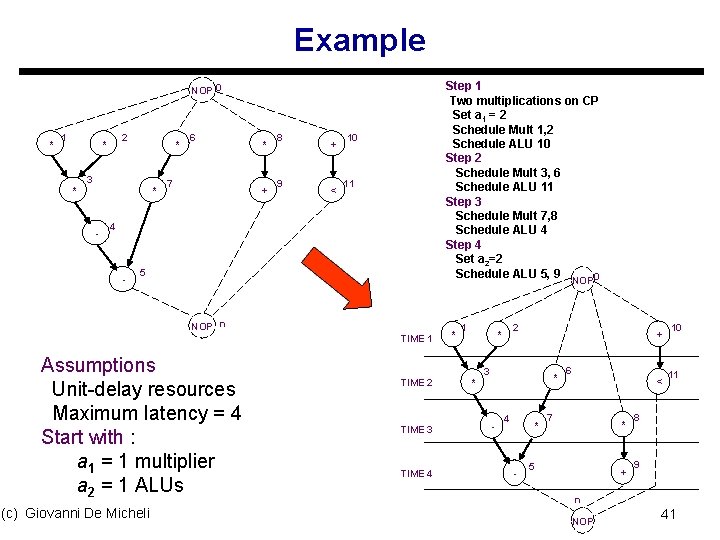
Example Step 1 Two multiplications on CP Set a 1 = 2 Schedule Mult 1, 2 Schedule ALU 10 Step 2 Schedule Mult 3, 6 Schedule ALU 11 Step 3 Schedule Mult 7, 8 Schedule ALU 4 Step 4 Set a 2=2 Schedule ALU 5, 9 NOP 0 * 1 2 * * * 3 * - 6 7 * + 8 9 + < 10 11 4 - 5 NOP n TIME 1 Assumptions Unit-delay resources Maximum latency = 4 Start with : a 1 = 1 multiplier a 2 = 1 ALUs (c) Giovanni De Micheli TIME 2 TIME 3 TIME 4 * 1 2 * * + 3 * - 4 * - 6 < 7 * 5 + 10 11 8 9 n NOP 41

Force-directed scheduling u. Heuristic scheduling methods [Paulin]: s Min latency subject to resource bound t s Variation of list scheduling : FDLS Min resource subject to latency bound t Schedule one operation at a time u. Rationale: s Reward uniform distribution of operations across schedule steps (c) Giovanni De Micheli 42

Force-directed scheduling definitions u. Operation interval: s Mobility plus one (μi +1) s Computed by ASAP and ALAP scheduling [ t. S , t. L] u. Operation probability pi (l): s Probability of executing in a given step 1/ ( μi + 1) inside interval; 0 elsewhere u. Operation-type distribution qk (l): s Sum of the operation probabilities for each type (c) Giovanni De Micheli 43

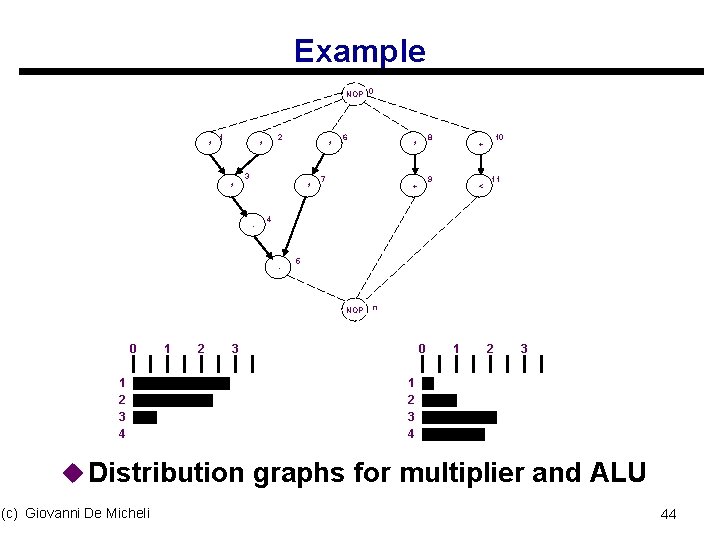
Example NOP 0 * 1 2 * * 3 * * - 6 7 1 2 3 4 2 < 11 5 NOP 1 9 + 10 + 4 - 0 8 * n 3 0 1 2 3 4 u Distribution graphs for multiplier and ALU (c) Giovanni De Micheli 44

Force u. Used as priority function u. Force is related to concurrency: s Sort operations for least force u. Mechanical analogy: s Force = constant x displacement t t Constant = operation-type distribution Displacement = change in probability (c) Giovanni De Micheli 45

Forces related to the assignment of an operation to a control step u. Self-force: s Sum of forces to feasible schedule steps s Self-force for operation vi in step l Σ m in interval qk(m) (δlm – pi(m)) u. Predecessor/successor-force: s Related to the predecessors/successors t t Fixing an operation timeframe restricts timeframe of predecessors/successors Ex: Delaying an operation implies delaying its successors (c) Giovanni De Micheli 46

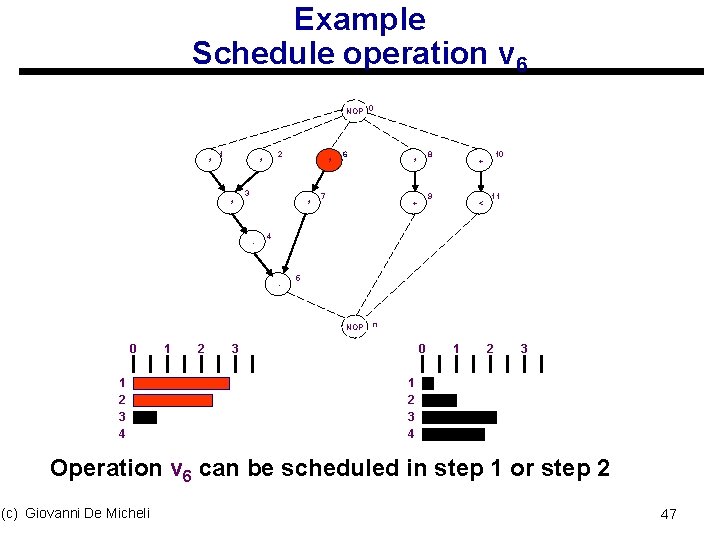
Example Schedule operation v 6 NOP 0 * 1 2 * * 3 * * - 6 7 1 2 3 4 2 < 11 5 NOP 1 9 + 10 + 4 - 0 8 * n 3 0 1 2 3 4 Operation v 6 can be scheduled in step 1 or step 2 (c) Giovanni De Micheli 47

Example: operation v 6 u Op v 6 can be scheduled in the first two steps p ( 1 ) = 0. 5; p (2) = 0. 5; p ( 3 ) = 0; p ( 4 ) = 0 u Distribution: q ( 1 ) = 2. 8; q ( 2 ) = 2. 3 u Assign v 6 to step 1: s variation in probability 1 – 0. 5 = 0. 5 for step 1 s variation in probability 0 – 0. 5 = -0. 5 for step 2 u Self-force: 2. 8 * 0. 5 – 2. 3 * 0. 5 = + 0. 25 u No successor force (c) Giovanni De Micheli 48

Example: operation v 6 u Assign v 6 to step 2: s variation in probability 0 – 0. 5 = -0. 5 for step 1 s variation in probability 1 – 0. 5 = 0. 5 for step 2 u Self-force: - 2. 8 * 0. 5 + 2. 3 * 0. 5 = - 0. 25 u Successor-force: s Operation v 7 assigned to step 3 s Succ. force is 2. 3 ( 0 - 0. 5 ) + 0. 8 ( 1 – 0. 5 ) = -. 75 u Total force = -1 (c) Giovanni De Micheli 49

Example: operation v 6 u. Total force in step 1 = + 0. 25 u. Total force in step 2 = -1 u. Conclusion: s Least force is for step 2 s Assigning v 6 to step 2 reduces concurrency (c) Giovanni De Micheli 50

Force-directed scheduling algorithm for minimum resources FDS ( G ( V, E ), λ ) { repeat { Compute/update the time-frames; Compute the operation and type probabilities; Compute the self-forces, p/s-forces and total forces; Schedule the op. with least force; } until (all operations are scheduled) return (t); } (c) Giovanni De Micheli 51

Scheduling and chaining u Consider propagation delays of resources not in terms of cycles u Use scheduling to chain multiple operations in the same control step u Useful technique to explore effect of cycle-time on area/latency trade-off u Algorithms: s ILP, ALAP/ASAP, list scheduling (c) Giovanni De Micheli 52

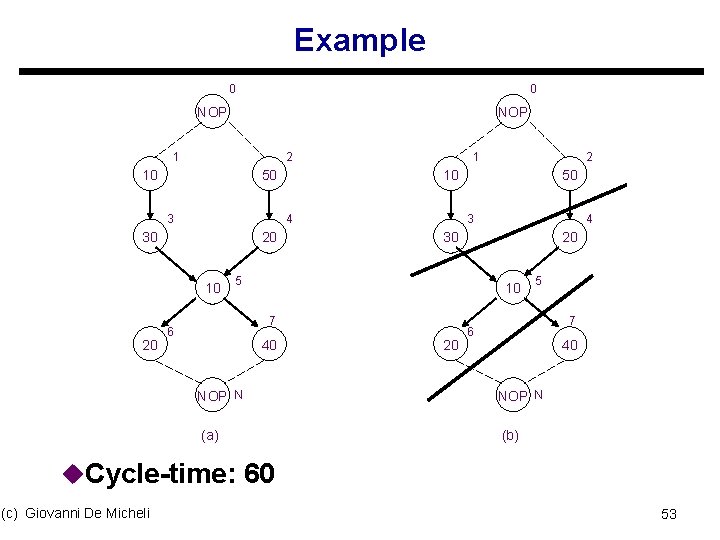
Example 0 0 NOP 1 2 10 50 3 20 10 50 3 4 30 20 5 10 7 6 2 10 4 30 20 1 40 20 5 7 6 40 NOP N (a) (b) u. Cycle-time: 60 (c) Giovanni De Micheli 53

Summary u Scheduling determines area/latency trade-off u Intractable problem in general: s Heuristic algorithms s ILP formulation (small-case problems) u Several heuristic formulations s List scheduling is the fastest and most used s Force-directed scheduling tends to yield good results u Several extensisons s Chaining (c) Giovanni De Micheli 54