ENGINEERING OPTIMIZATION Methods and Applications A Ravindran K

ENGINEERING OPTIMIZATION Methods and Applications A. Ravindran, K. M. Ragsdell, G. V. Reklaitis Book Review Page 1

Chapter 9: Direction Generation Methods Based on Linearization Part 1: Ferhat Dikbiyik Part 2: Mohammad F. Habib Review Session July 30, 2010 Page 2

The Linearization-based algorithms in Ch. 8 • LP solution techniques to specify the sequence of intermediate solution points. The linearized subproblem at this point is updated The exact location of next iterate is determined by LP The linearized subproblem cannot be expected to give a very good estimate of either boundaries of the feasible solution region or the contours of the objective function Page 3

Good Direction Search Rather than relying on the admittedly inaccurate linearization to define the precise location of a point, it is more realistic to utilize the linear approximations only to determine a locally good direction for search. Page 4

Outline • 9. 1 Method of Feasible Directions • 9. 2 Simplex Extensions for Linearly Constrained Problems • 9. 3 Generalized Reduced Gradient Method • 9. 4 Design Application Page 5

9. 1 Method of Feasible Directions G. Zoutendijk Mehtods of Feasible Directions, Elsevier, Amsterdam, 1960 Page 6

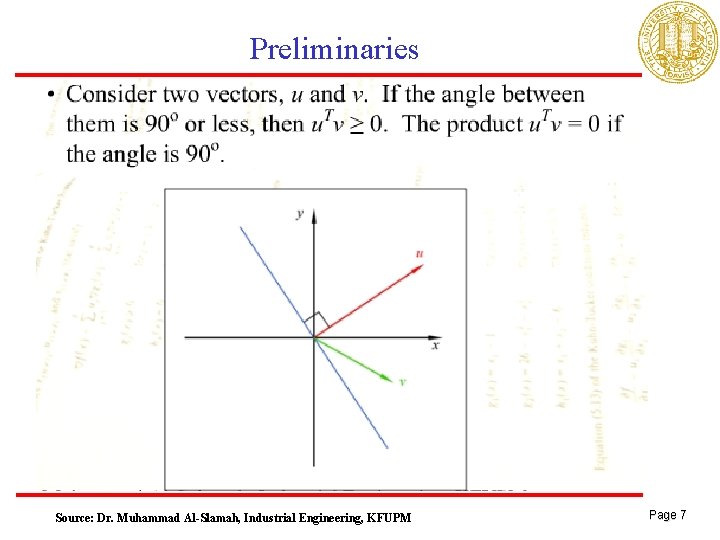
Preliminaries Source: Dr. Muhammad Al-Slamah, Industrial Engineering, KFUPM Page 7

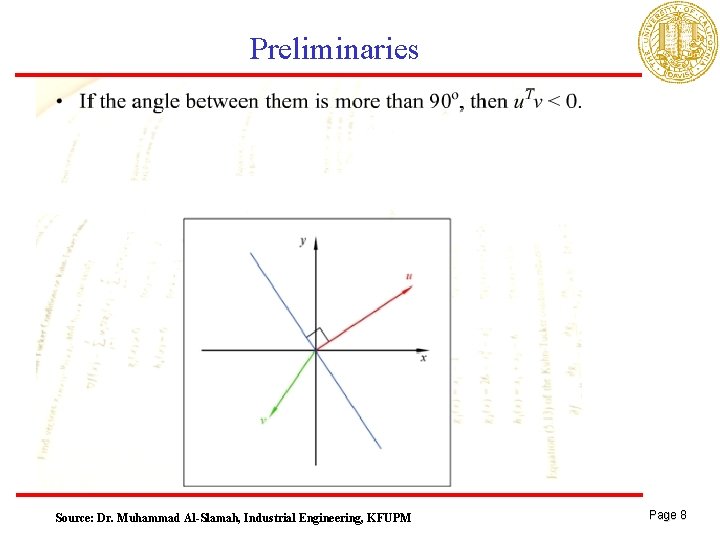
Preliminaries Source: Dr. Muhammad Al-Slamah, Industrial Engineering, KFUPM Page 8

9. 1 Method of Feasible Directions • Suppose that constraints. is a starting point that satisfies all • and suppose that a certain subset of these constraints are binding at. Page 9

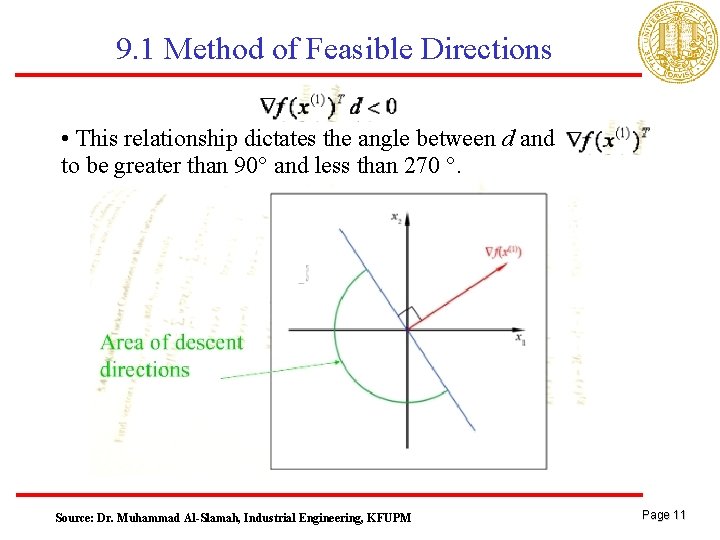
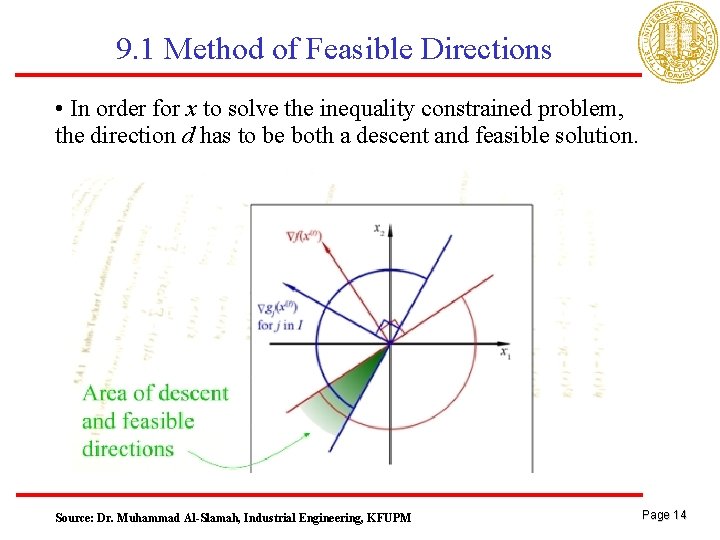
9. 1 Method of Feasible Directions • Suppose is a feasible point • Define x as • The first order Taylor approximation of f(x) is given by • In order for , we have to have • A direction satisfying this relationship is called a descent direction Page 10

9. 1 Method of Feasible Directions • This relationship dictates the angle between d and to be greater than 90° and less than 270 °. Source: Dr. Muhammad Al-Slamah, Industrial Engineering, KFUPM Page 11

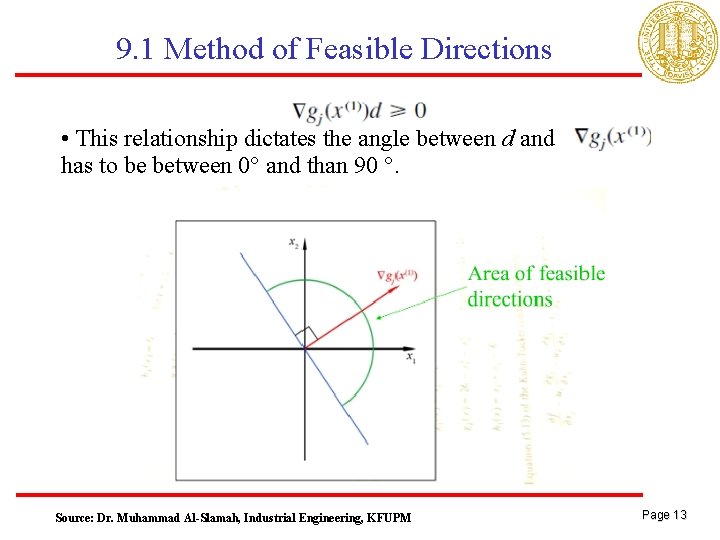
9. 1 Method of Feasible Directions • The first order Taylor approximation for constraints • And with assumption (because it’s binding) • In order for x to be a feasible, hence • Any direction d satisfying this relationship called a feasible direction Page 12

9. 1 Method of Feasible Directions • This relationship dictates the angle between d and has to be between 0° and than 90 °. Source: Dr. Muhammad Al-Slamah, Industrial Engineering, KFUPM Page 13

9. 1 Method of Feasible Directions • In order for x to solve the inequality constrained problem, the direction d has to be both a descent and feasible solution. Source: Dr. Muhammad Al-Slamah, Industrial Engineering, KFUPM Page 14

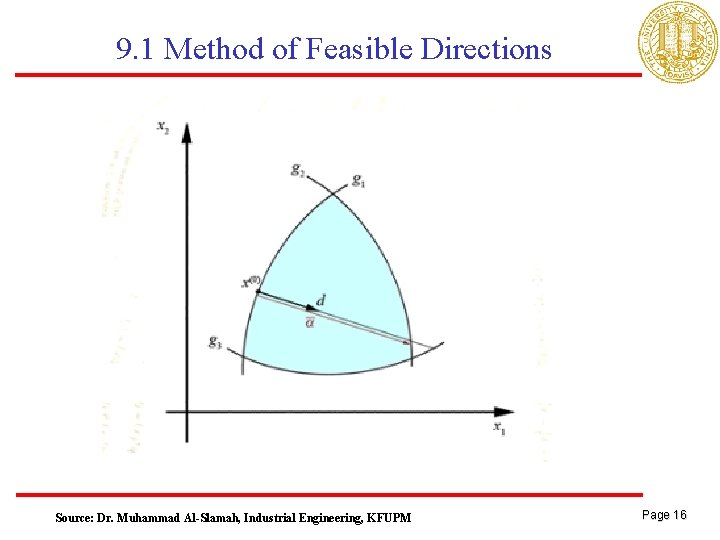
9. 1 Method of Feasible Directions • Zoutendijk’s basic idea is at each stage of iteration to determine a vector d that will be both a feasible direction and a descent direction. This is accomplished numerically by finding a normalized direction vector d and a scalar parameter θ > 0 such that and θ is as large as possible. Page 15

9. 1 Method of Feasible Directions Source: Dr. Muhammad Al-Slamah, Industrial Engineering, KFUPM Page 16

9. 1. 1 Basic Algorithm • The active constraint set is defined as for some small Page 17

9. 1. 1 Basic Algorithm • Step 1. Solve the linear programming problem Label the solution and Page 18

9. 1. 1 Basic Algorithm • Step 2. If the iteration terminates, since no further improvement is possible. Otherwise, determine If no exists, set Page 19

9. 1. 1 Basic Algorithm • Step 3. Find Set such that and continue. Page 20

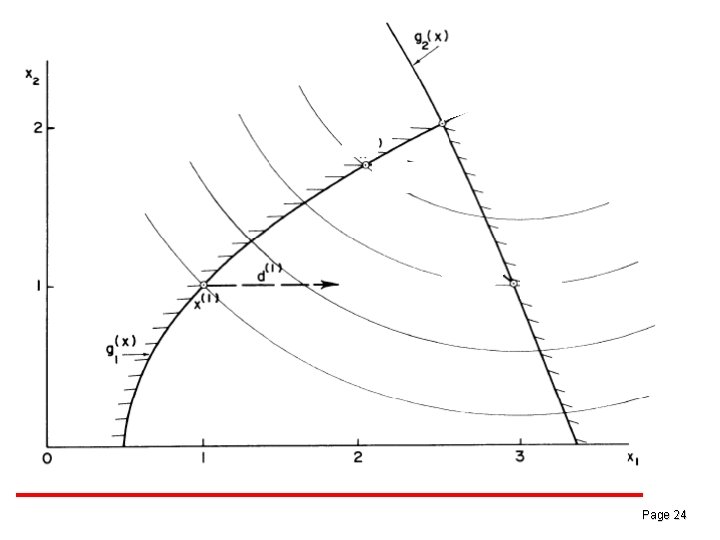
Example 9. 1 , since g_1 is the only binding constraint. Page 21

Example 9. 1 We must search along the ray to find the point at which boundary of feasible region is intersected Page 22

Example 9. 1 Since is positive for all α ≥ 0 and is not violated as α is increased. To determine the point at which will be intersected, we solve Finally, we search on α over range determine the optimum of to Page 23

Example 9. 1 Page 24

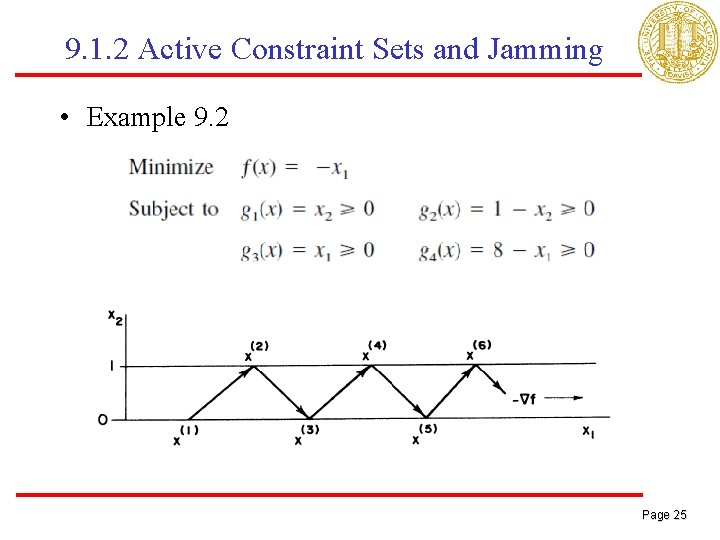
9. 1. 2 Active Constraint Sets and Jamming • Example 9. 2 Page 25

9. 1. 2 Active Constraint Sets and Jamming • The active constraint set used in the basic form of feasible direction algorithm, namely, cannot only slow down the process of iterations but also lead to convergence to points that are not Kuhn-Tucker points. • This type of false convergence is known as jamming Page 26

9. 1. 2. 1 ε-Perturbation Method 1. At iteration point and with given , define and carry out step 1 of the basic algorithm. 2. Modify step 2 with the following: If , set and continue. However, if , set and proceed with line search of the basic method. If , then a Kuhn. Tucker point has been found. With this modification, it is efficient to set ε rather loosely initially so as to include the constraints in a larger neighborhood of the point. Then, as the iterations proceed, the size of the neighborhood will be reduced only when it is found to be necessary. Page 27

9. 1. 2. 2 Topkis-Veinott Variant • This approach simply dispense with the active constraint concept altogether and redefine the direction-finding subproblem as follows: If the constraint loose at , then the selection of d is less affected by constraint j, because the positive constraint value will counterbalance the effect of the gradient term. This ensures that no sudden changes are introduced in the search direction. Page 28

9. 2 Simplex Extensions for Linearly Constrained Problems • At a given point, the number of directions that are both descent and feasible directions is generally infinite. • In the case of linear programs, the generation of search directions was simplified by changing one variable at a time; feasibility was ensured by checking sign restrictions, and descent was ensured by selecting a variable with negative relative-cost coefficient. Page 29

9. 2. 1 Convex Simplex Method N components M rows • Given a feasible point two sets: • the basic variables the x variable is partitioned into , which are all positive • the nonbasic variables an M vector , which are all zero an N-M vector Page 30

9. 2. 1 Convex Simplex Method Page 31

9. 2. 1 Convex Simplex Method The relative-cost coefficients The nonbasic variable to enter is selected by finding such that The basic variable to leave the basis is selected using the minimum-ratio rule. That is, we find r such that elements of matrix Page 32

9. 2. 1 Convex Simplex Method • The new feasible solution and all other variables zero. At this point, the variables and are relabeled. Since an exchange will have occurred, will be redefined. The matrix is recomputed another cycle of iterations is begun. Page 33

9. 2. 1 Convex Simplex Method • The application of same algorithm to linearized form of a non-linear objective function: • The relative-cost factor: Page 34

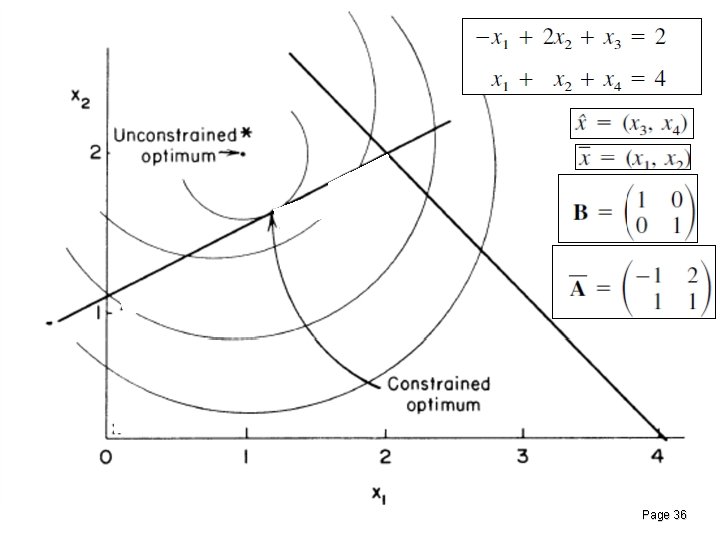
Example 9. 4 Page 35

Example 9. 4 Page 36

Example 9. 4 The relative-cost factor: Page 37

Example 9. 4 The nonbasic variable to enter will be The basic variable to leave will be , since Page 38

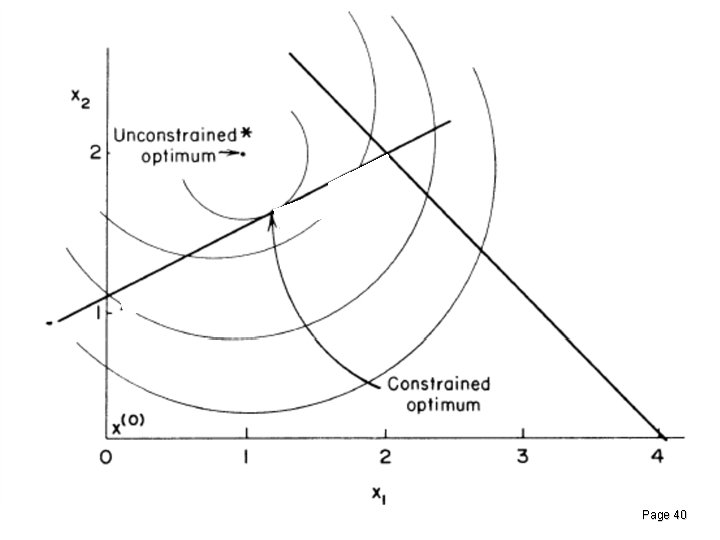
Example 9. 4 • The new point is thus A line search between and is now required to locate minimum of. Note that remains at 0, while changes as given by Page 39

Example 9. 4 Page 40

Convex Simplex Algorithm Page 41

Convex Simplex Algorithm Page 42

9. 2. 2 Reduced Gradient Method • The nonbasic variable direction vector: • This definition ensures that when for all i, the Kuhn-Tucker conditions are satisfied. Page 43

9. 2. 2 Reduced Gradient Method • In the first case, the limiting α value will be given by If all , then set • In the second case, If all , then set Page 44

Reduced Gradient Algorithm Page 45

Page 46