The regular 3 D Platonic Solids All faces

The (regular, 3 D) Platonic Solids • All faces, all edges, all corners, are the same. • They are composed of regular 2 D polygons: • There were infinitely many 2 D n-gons! • How many of these regular 3 D solids are there?

Making a Corner for a Platonic Solid Put at least 3 polygons around a shared vertex to form a real physical 3 D corner! • Putting 3 squares around a vertex leaves a large (90º) gap; • Forcefully closing this gap makes the structure pop out into 3 D space, forming the corner of a cube. • We can also do this with 3 pentagons: dodecahedron.

Why Only 5 Platonic Solids? Lets try to build all possible ones: • from triangles: 3, 4, or 5 around a corner: • from squares: only 3 around a corner: • from pentagons: only 3 around a corner: • from hexagons: “floor tiling”, does not bend! • higher n-gons: do not fit around a vertex without undulations (forming saddles); Now the edges are no longer all alike!

Utah Teapot The “Sixth Platonic Solid” -- if you belong to the Computer Graphics community.

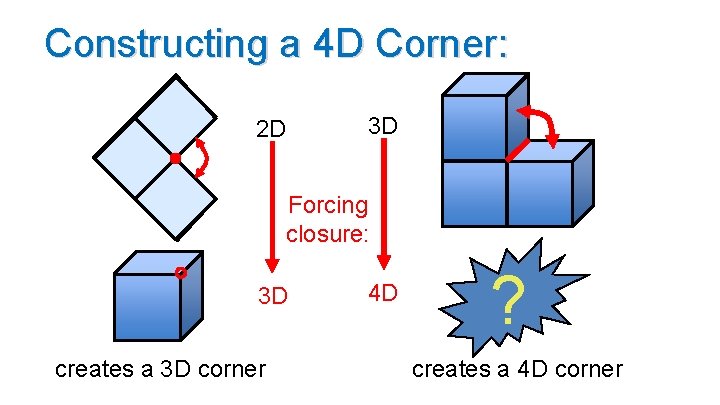
Constructing a 4 D Corner: 2 D 3 D Forcing closure: 3 D creates a 3 D corner 4 D ? creates a 4 D corner

How Do We Find All 4 D Polytopes? • Reasoning by analogy helps a lot: -- How did we find all the Platonic solids? • Now: Use the Platonic solids as “tiles” and ask: – What can we build from tetrahedra? – or from cubes? – or from the other 3 Platonic solids? Need to look at dihedral angles: Tetrahedron: 70. 5°, Octahedron: 109. 5°, Cube: 90°, Dodecahedron: 116. 5°, Icosahedron: 138. 2°.

All Regular Polytopes in 4 D Using Tetrahedra (70. 5°): 3 around an edge (211. 5°) (5 cells) Simplex 4 around an edge (282. 0°) (16 cells) Cross-Polytope 5 around an edge (352. 5°) (600 cells) 600 -Cell Using Cubes (90°): 3 around an edge (270. 0°) (8 cells) Hypercube Using Octahedra (109. 5°): 3 around an edge (328. 5°) (24 cells) 24 -Cell Using Dodecahedra (116. 5°): 3 around an edge (349. 5°) (120 cells) 120 -Cell Using Icosahedra (138. 2°): None! : dihedral angle is too large ( 414. 6°).

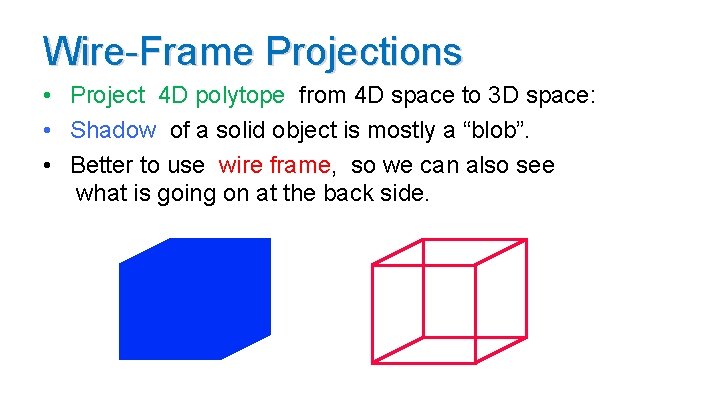
Wire-Frame Projections • Project 4 D polytope from 4 D space to 3 D space: • Shadow of a solid object is mostly a “blob”. • Better to use wire frame, so we can also see what is going on at the back side.

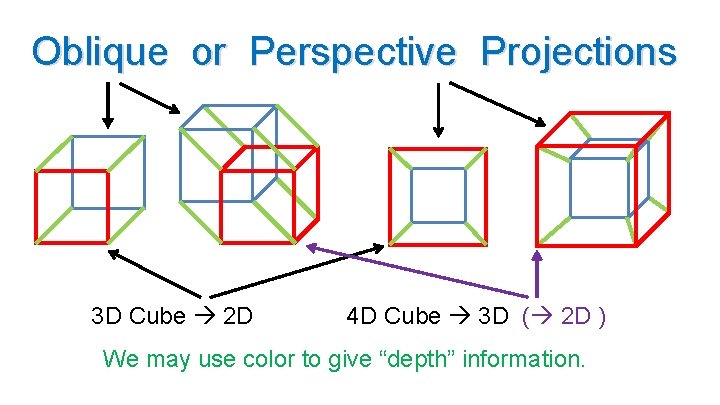
Oblique or Perspective Projections 3 D Cube 2 D 4 D Cube 3 D ( 2 D ) We may use color to give “depth” information.

Constructing 4 D Regular Polytopes • Let's construct all 4 D regular polytopes -- or rather, “good” projections of them. • What is a “good” projection ? – Maintain as much of the symmetry as possible; – Get a good feel for the structure of the polytope. • What are our options ? A parade of various projections

5 -Cell or “ 4 D Simplex” • 5 cells (tetrahedra), • 10 faces (triangles), • 10 edges, • 5 vertices. (Perspective projection)

16 -Cell or “ 4 D-Cross Polytope” • 16 cells (tetrahedra), • 32 faces, • 24 edges, • 8 vertices.

4 D-Hypercube or “Tessaract” • 8 cells (cubes), • 24 faces (squares), • 32 edges, • 16 vertices.

24 -Cell • 24 cells (octahedra), • 96 faces, • 96 edges, • 24 vertices. 1152 symmetries!

24 -Cell Showing four congruent Hamiltonian cycles (in red, green, yellow, blue), each visiting every vertex exactly once.

120 -Cell • 120 cells (dodecahedra), • 720 faces (pentagons), • 1200 edges, • 600 vertices.

600 -Cell • 600 cells (tetrahedra), • 1200 faces, • 720 edges, • 120 vertices.

Polytopes in Higher Dimensions • Use 4 D tiles, look at “dihedral” angles between cells: 5 -Cell: 75. 5°, Tessaract: 90°, 16 -Cell: 120°, 24 -Cell: 120°, 120 -Cell: 144°, 600 -Cell: 164. 5°. • Most 4 D polytopes are too round … But we can use 3 or 4 5 -Cells, and 3 Tessaracts. • There are three methods by which we can generate regular polytopes for 5 D and for all higher dimensions.

“Dihedral Angles in Higher Dim. ” Consider the angle through which one cell has to be rotated to be brought in coincidence with an adjoining neighbor cell. Space 2 D Simplex Series 60° 3 D 70. 5° 4 D 75. 5° Cross 90° 109. 5° 120° Polytopes Measure 90° Polytopes 90° 5 D 78. 5° 6 D 80. 4° 90° 126. 9° 131. 8° 180° 90° 90°

Beyond 4 Dimensions … • What happens in higher dimensions ? • How many regular polytopes are there in 5, 6, 7, … dimensions ? Only THREE for each dimension! • Pictures for 6 D space: • Simplex with D+1 vertices, • Hypercube with 2 D vertices, • Cross-Polytope with 2 D vertices.

Hypercube Series • “Measure Polytope” Series • Consecutive perpendicular sweeps: 1 D 2 D 3 D 4 D This series extends to arbitrary dimensions!

4 D Hypercube Vertex-first Projection

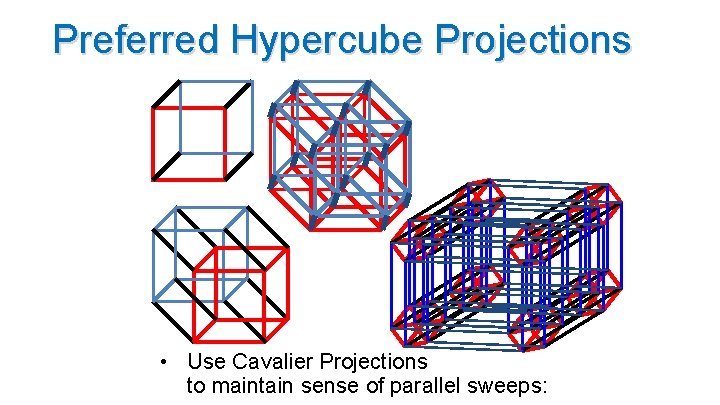
Preferred Hypercube Projections • Use Cavalier Projections to maintain sense of parallel sweeps:

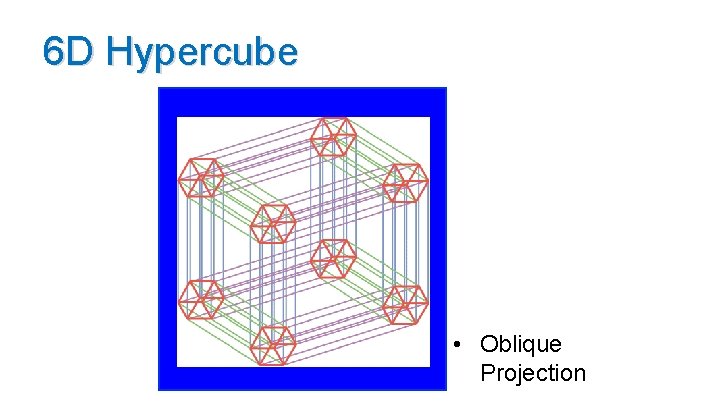
6 D Hypercube • Oblique Projection

6 D Zonohedron • Sweep symmetrically in 6 directions (in 3 D)

Simplex Series • Connect all the dots among n+1 equally spaced vertices: (Find next one above COG). 1 D 2 D 3 D This series also goes on indefinitely! The issue is how to make “nice” projections.

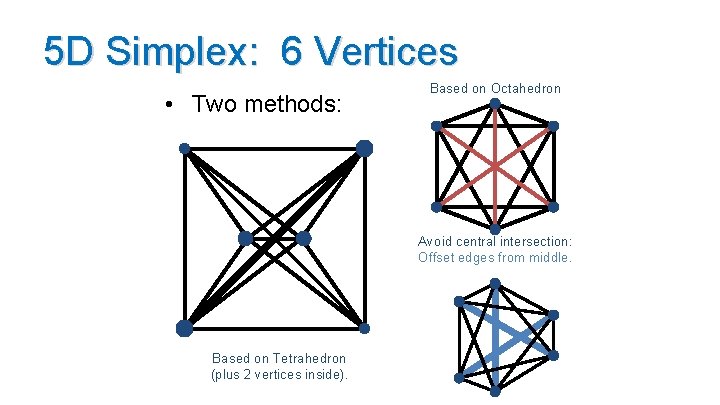
5 D Simplex: 6 Vertices • Two methods: Based on Octahedron Avoid central intersection: Offset edges from middle. Based on Tetrahedron (plus 2 vertices inside).

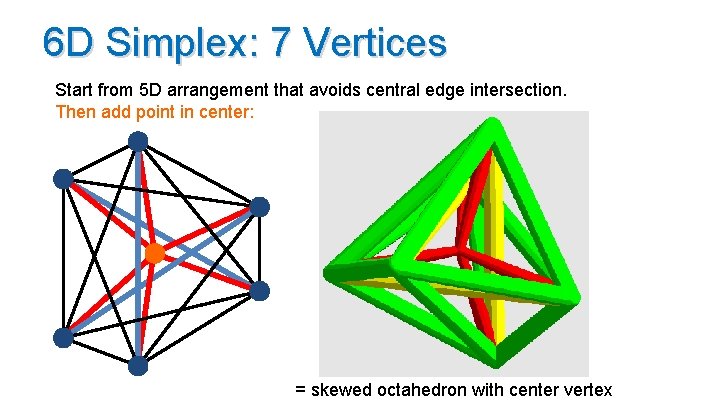
6 D Simplex: 7 Vertices Start from 5 D arrangement that avoids central edge intersection. Then add point in center: = skewed octahedron with center vertex

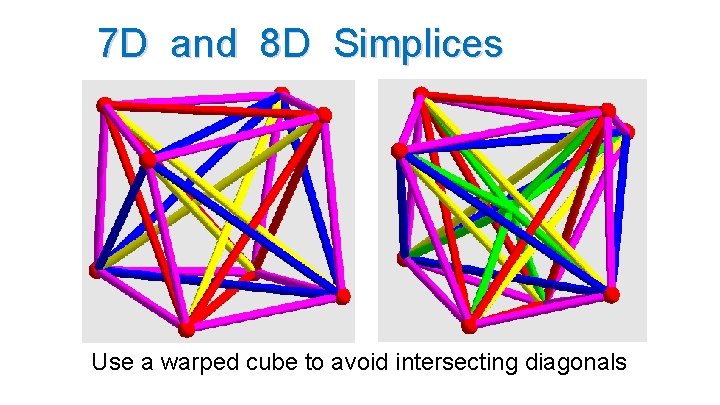
7 D and 8 D Simplices Use a warped cube to avoid intersecting diagonals

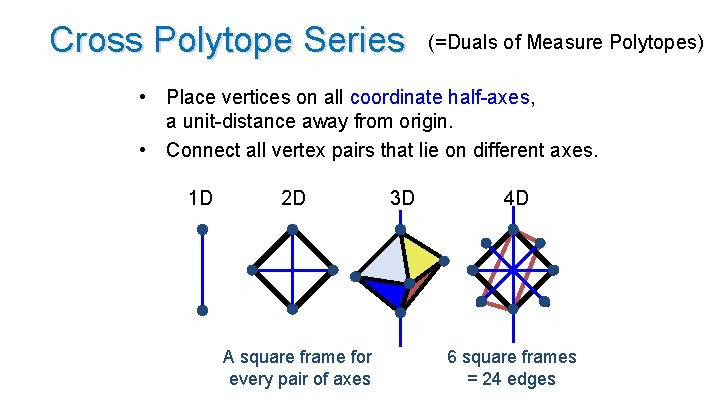
Cross Polytope Series (=Duals of Measure Polytopes) • Place vertices on all coordinate half-axes, a unit-distance away from origin. • Connect all vertex pairs that lie on different axes. 1 D 2 D A square frame for every pair of axes 3 D 4 D 6 square frames = 24 edges

4 D Cross Polytope … another model with three interwoven Hamiltonian cycles.

5 D Cross Polytope (10 vertices) Warped cube + 2 vertices

6 D Cross Polytope 12 vertices icosahedral symmetry (but edge-intersections)

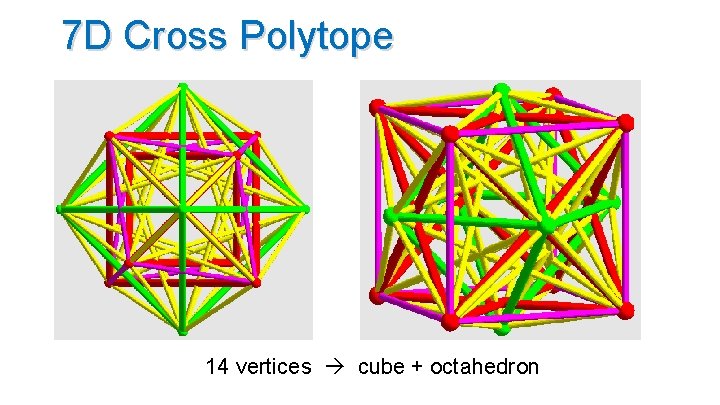
7 D Cross Polytope 14 vertices cube + octahedron

5 D and Beyond The three polytopes that result from the – Simplex series, – Cross polytope series, – Measure polytope series, Duals ! . . . is all there is in 5 D and beyond! Dim. # 2 D 3 D 4 D 5 D 6 D 7 D 8 D 9 D … 5 6 3 3 3 Luckily, we live in one of the interesting dimensions!