Regular Languages Regular Operations Closure Regular Languages We

Regular Languages, Regular Operations, Closure

Regular Languages • We say that a language L is regular iff there is a DFA that accepts L. • The regular languages is the set of languages that dfas accept.

Regular Operations The regular operations are the following: • Union (U) • Concatenation (o) • Star (*)

Regular Operations • • • L 1 U L 2 = {x|x L 1 or x L 2} L 1 o L 2 = {xy|x L 1 and y L 2} Lk = L o … o L, k times , L 0 = {ε} L* = Lk for any k ≥ 0 L+ = Lk for any k > 0

Regular Operations Examples L 1 = {a, b}, L 2 = {b, c} • L 1 U L 2= {a, b, c} • L 1 o L 2 = {ab, ac, bb, bc} • L 1 2 = {aa, ab, ba, bb} • L 1* = {ε, a, b, aa, ab, ba, bb, aaa, aab, aba, abb, baa, bab, bba, bbb, aaaa, aaab, aaba, …} • Σ* is the set of all possible strings of an alphabet Σ.

Closure To show that a set is closed under an operation we should prove that, if we apply the operation on members of the set then the result belongs in the set. Example: The set of natural numbers N is closed under +, because if we add any two numbers in N the result is still in N. However, N is not closed under -, since 3 -5 = -2 which is not in N. Question: Is Z closed under -? What about / ?

Regular Languages are closed under union. • We should prove that if L 1 and L 2 are regular then L = L 1 L 2 is also regular. • Since L 1 and L 2 are regular there exist DFAs M 1 and M 2 that accept them. • It suffices to show that there exist a DFA M that accepts L. • We construct a DFA that accepts L.

Proof idea • I want to construct a DFA M that will simulate both M 1 and M 2 running in parallel. This machine should keep track of what happened to either machine after following a symbol a of the alphabet.

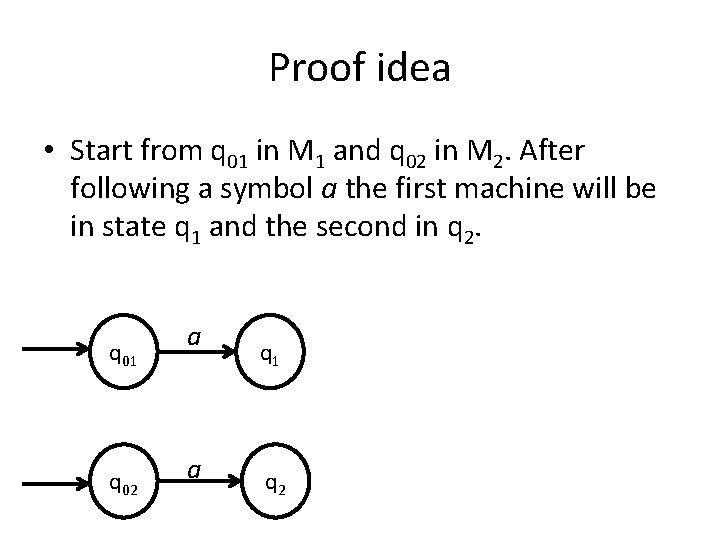
Proof idea • Start from q 01 in M 1 and q 02 in M 2. After following a symbol a the first machine will be in state q 1 and the second in q 2. q 01 q 02 a a q 1 q 2

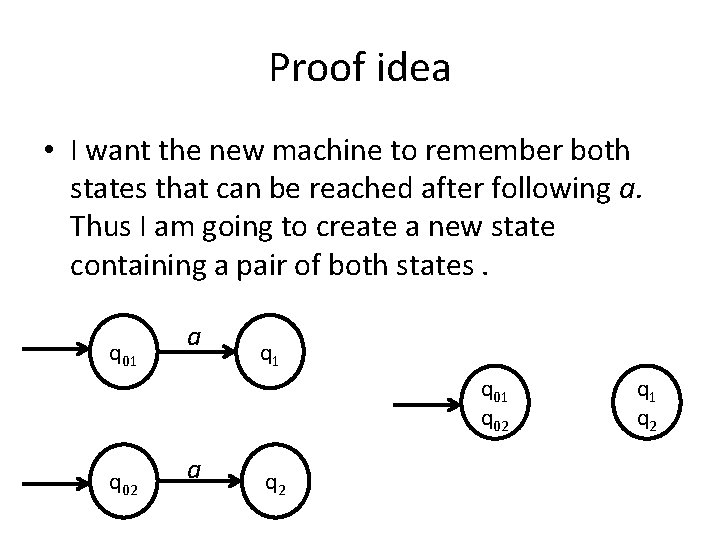
Proof idea • I want the new machine to remember both states that can be reached after following a. Thus I am going to create a new state containing a pair of both states. q 01 a q 1 q 02 a q 2 q 1 q 2

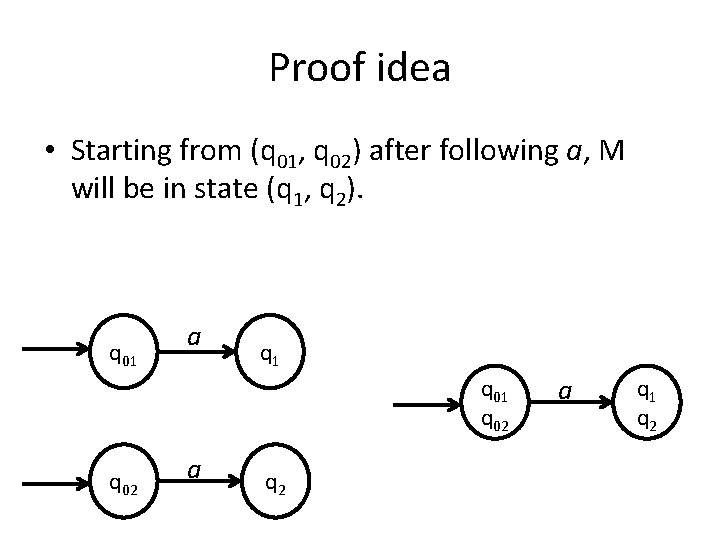
Proof idea • Starting from (q 01, q 02) after following a, M will be in state (q 1, q 2). q 01 a q 1 q 02 a q 1 q 2

Proof idea • Now it is left to find which of these pairs of states will be the accepting ones. • I want to construct a DFA M that accepts the union L 1 U L 2, that is all the strings which are accepted by either of the DFAs M 1, M 2.

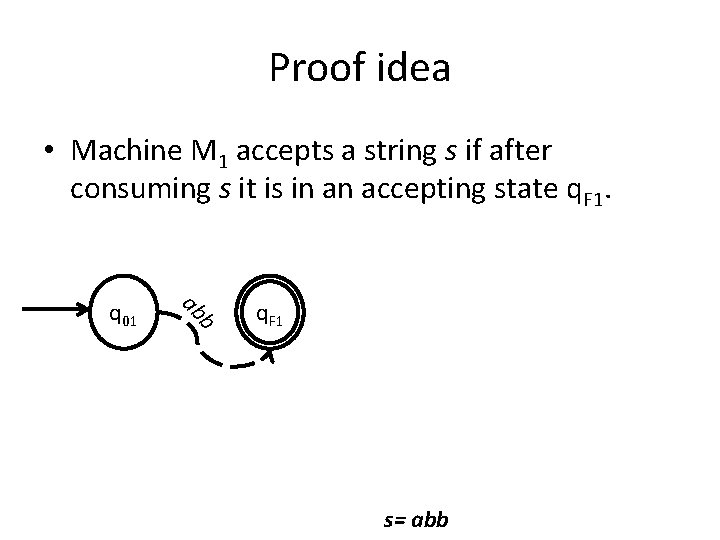
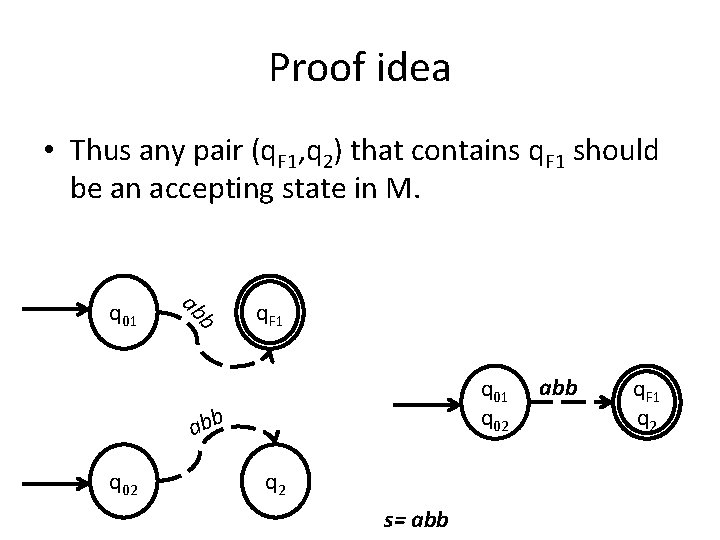
Proof idea • Machine M 1 accepts a string s if after consuming s it is in an accepting state q. F 1. b ab q 01 q. F 1 s= abb

Proof idea • Thus any pair (q. F 1, q 2) that contains q. F 1 should be an accepting state in M. b ab q 01 q. F 1 q 02 abb q 02 q 2 s= abb q. F 1 q 2

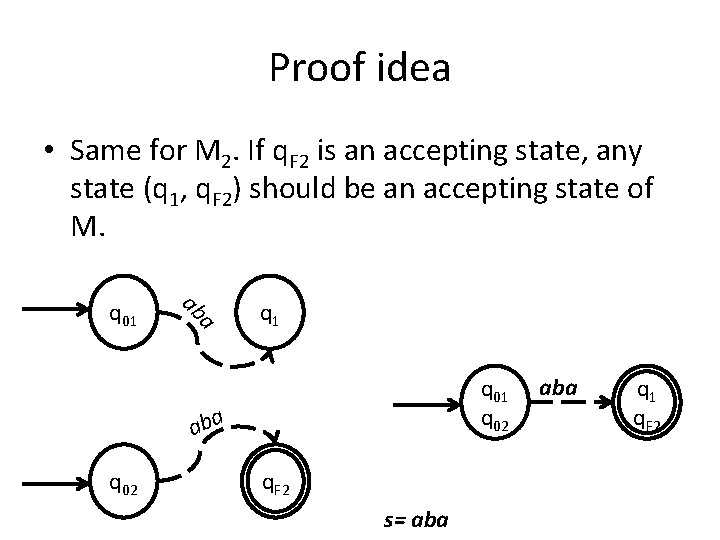
Proof idea • Same for M 2. If q. F 2 is an accepting state, any state (q 1, q. F 2) should be an accepting state of M. a ab q 01 q 02 aba q 02 q. F 2 s= aba q 1 q. F 2

A DFA that accepts L 1 U L 2 Assume that M 1 = {Q 1, Σ , δ 1 , q 01 , F 1} and M 2 = {Q 2, Σ , δ 2 , q 02 , F 2}. Then M = {Q, Σ, δ, q 0, F}, where • Q = Q 1 x Q 2 • δ((q 1, q 2), a) = (δ 1(q 1, a), δ 2(q 2, a)) • q 0 = (q 01, q 02) • F = (Q 1 x F 2) (F 1 x Q 2)

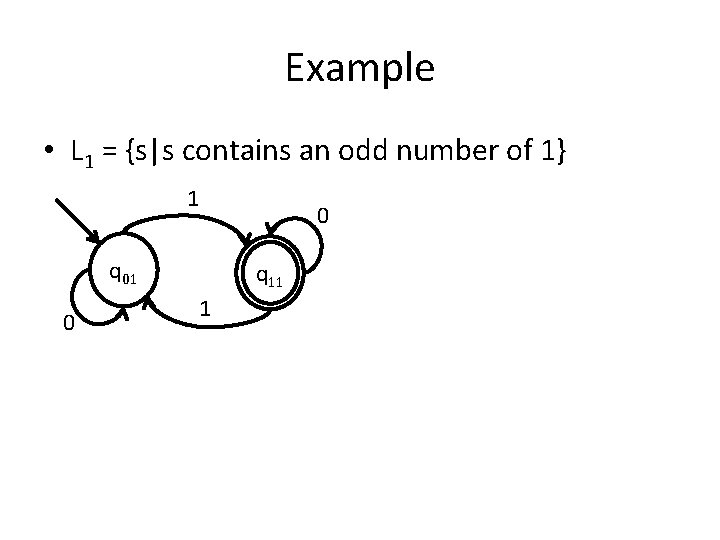
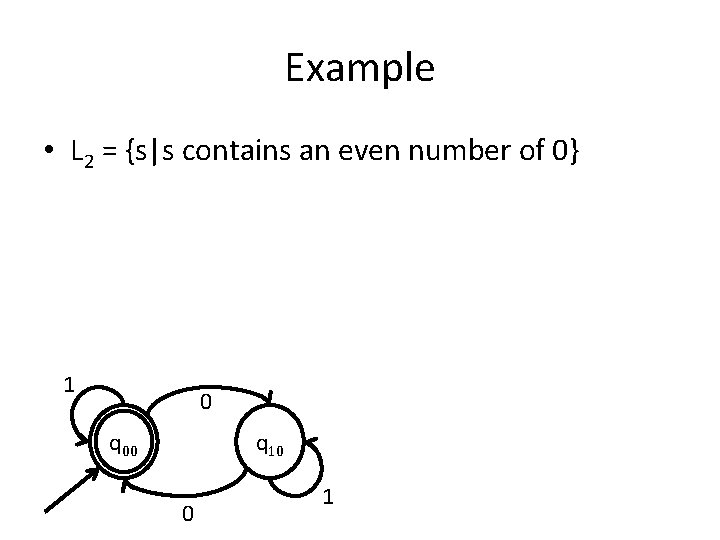
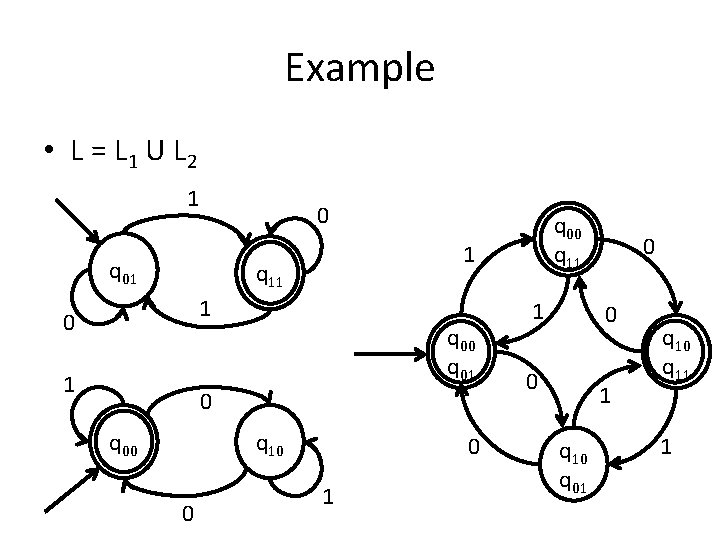
Example • Construct a DFA that accepts the language L = L 1 U L 2, where : – L 1 = {s|s contains an odd number of 1} and – L 2 = {s|s contains an even number of 0}.

Example • L 1 = {s|s contains an odd number of 1} 1 q 01 0 0 q 11 1

Example • L 2 = {s|s contains an even number of 0} 1 0 q 00 q 10 0 1

Example • L = L 1 U L 2 1 0 q 01 1 q 11 1 0 q 01 1 0 q 00 q 10 0 q 00 q 11 0 1 1 0 0 0 1 q 10 q 01 q 10 q 11 1

Question • What if I would like to construct a DFA that accepts the intersection of two regular languages? (in other words show that the regular languages are closed under the intersection).