Teoria della programmazione lineare Corso di Ricerca Operativa

















































- Slides: 72

Teoria della programmazione lineare Corso di Ricerca Operativa A. A. 2016 -2017

Argomenti Concetti preliminari Condizioni geometriche di ottimalità e illimitatezza Condizioni algebriche di ottimalità

Concetti preliminari

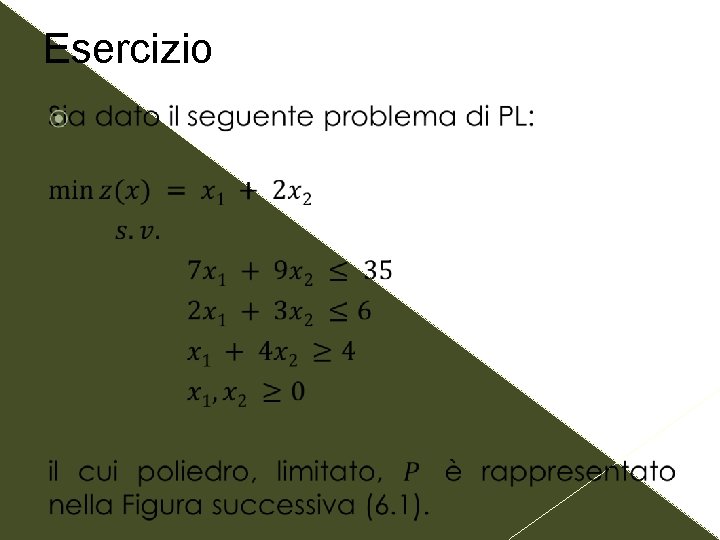
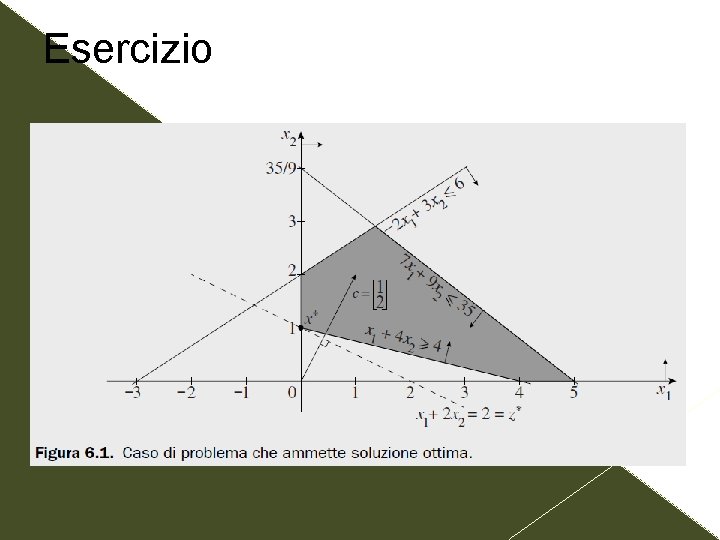
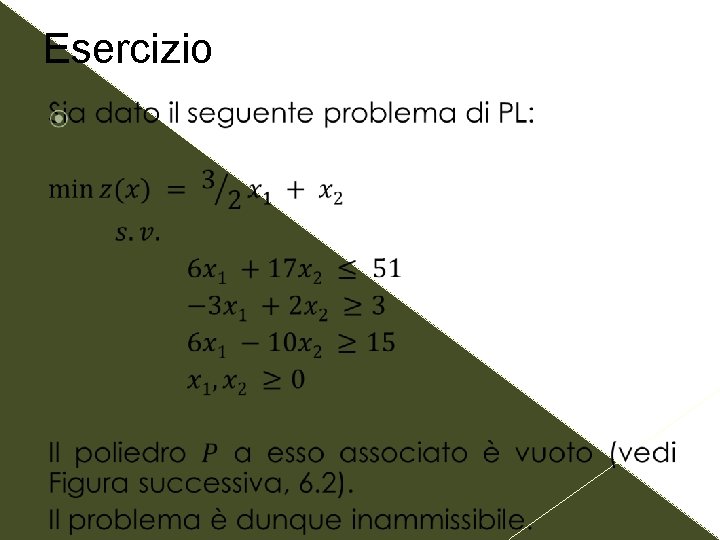
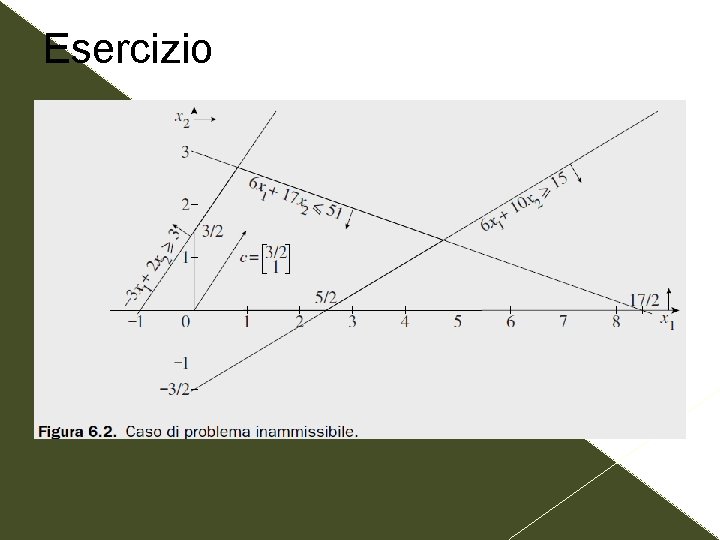
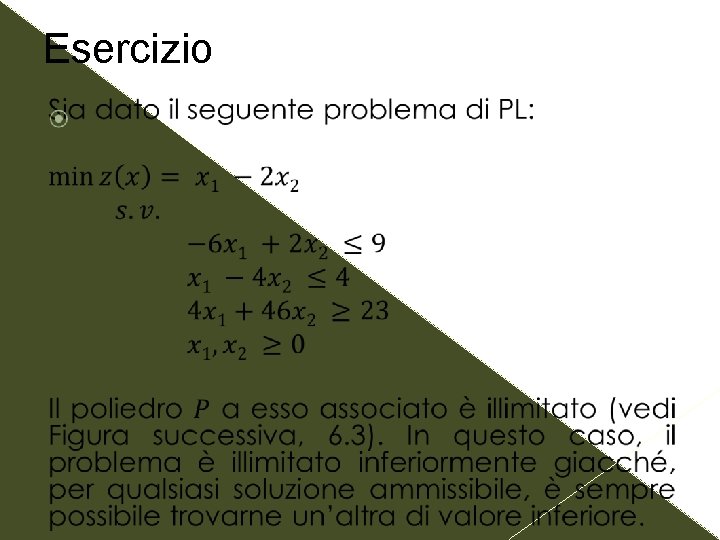
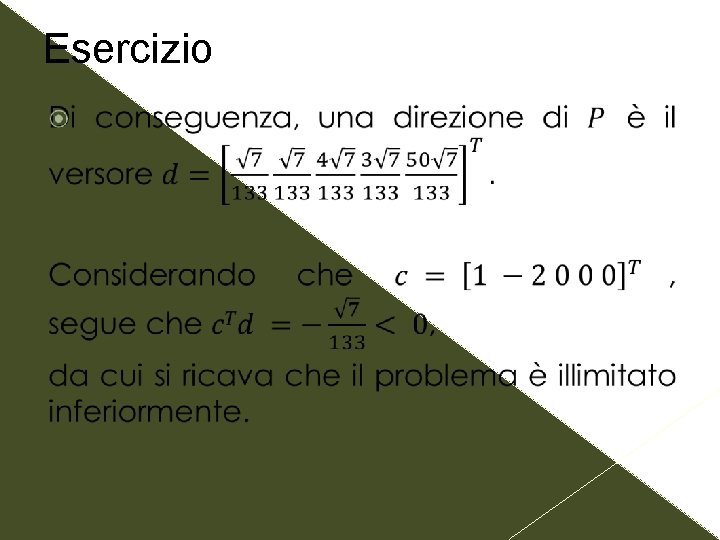
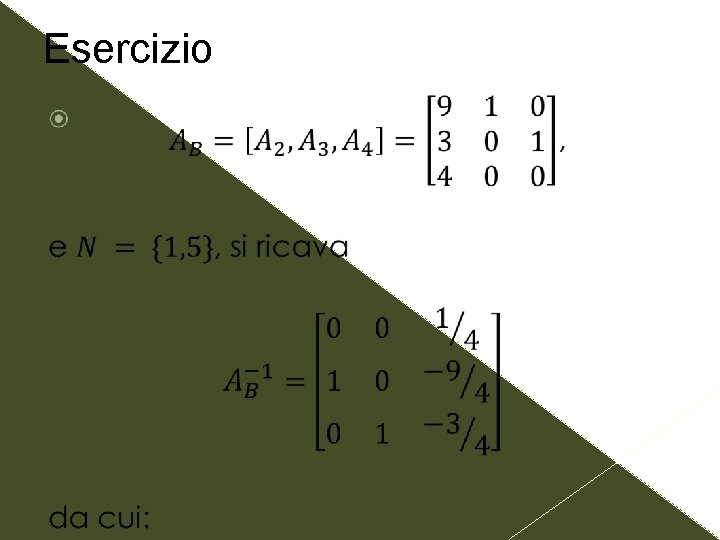
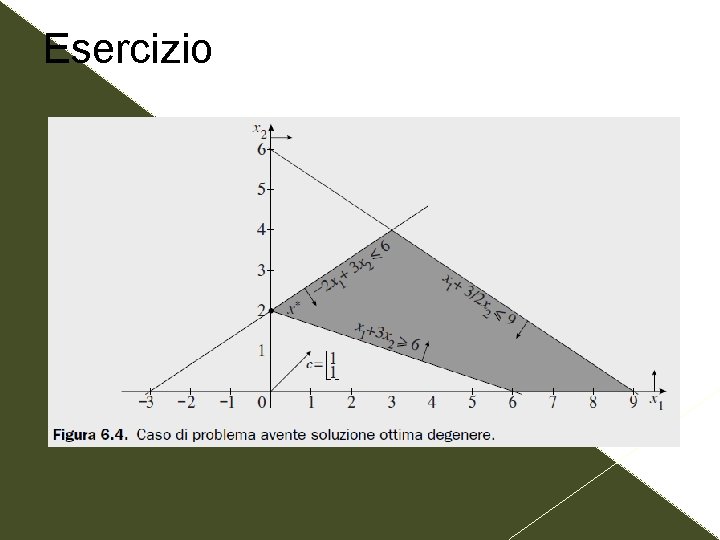
Esercizio

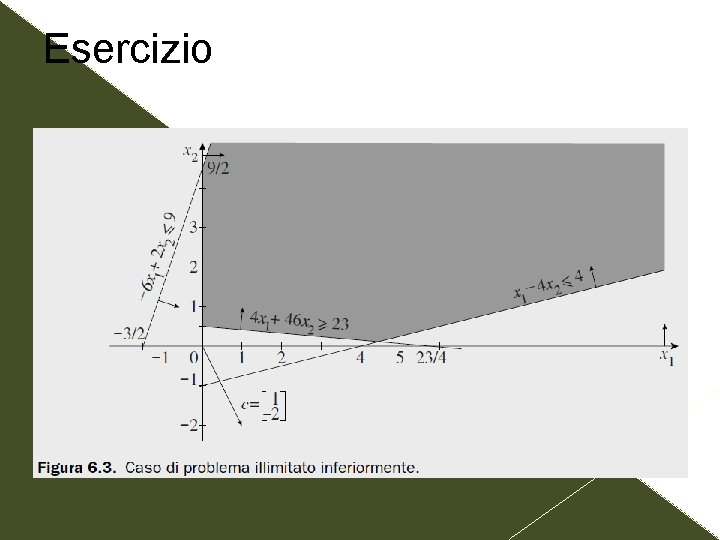
Esercizio

Esercizio

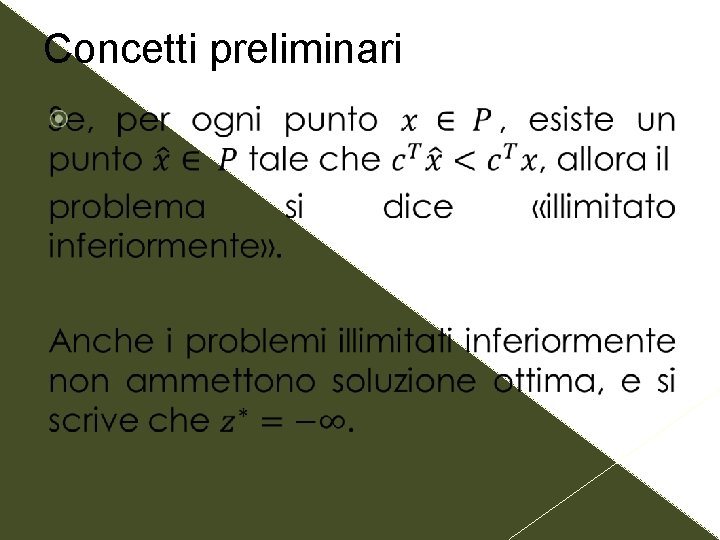
Concetti preliminari

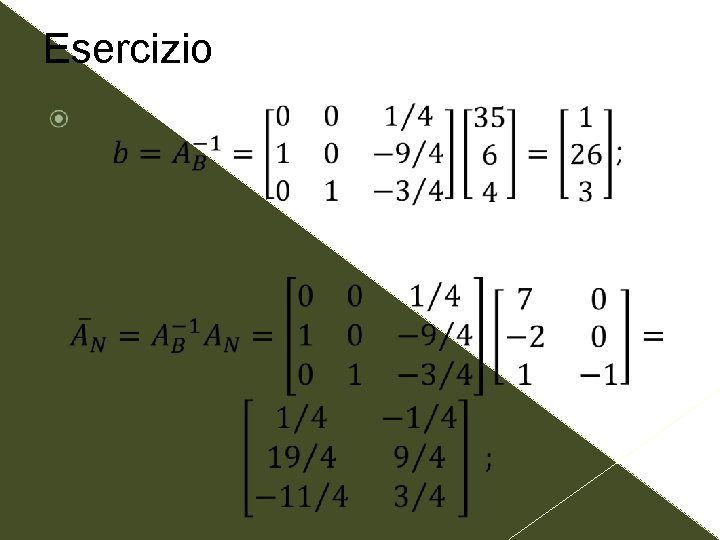
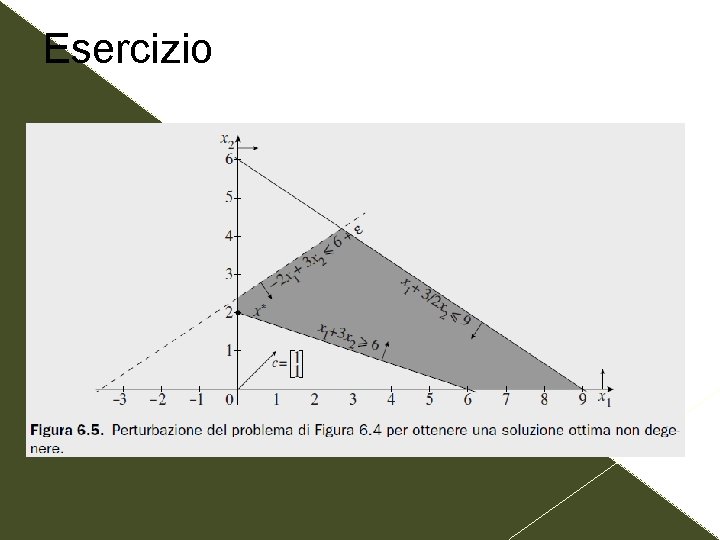
Esercizio

Esercizio

Concetti preliminari

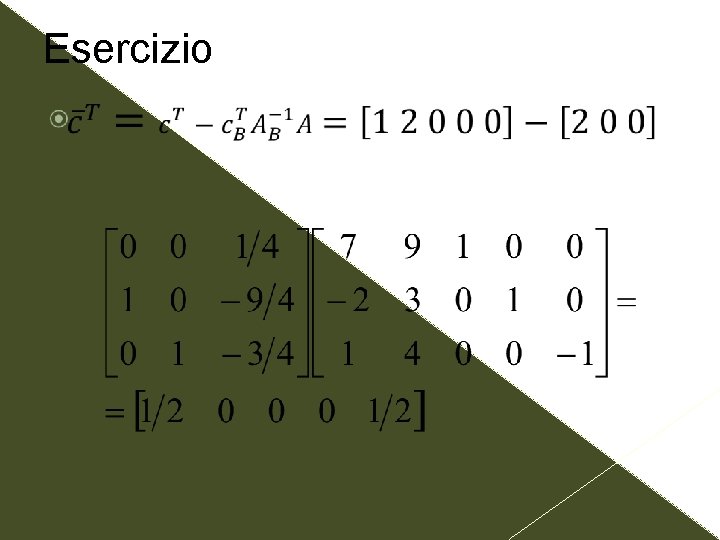
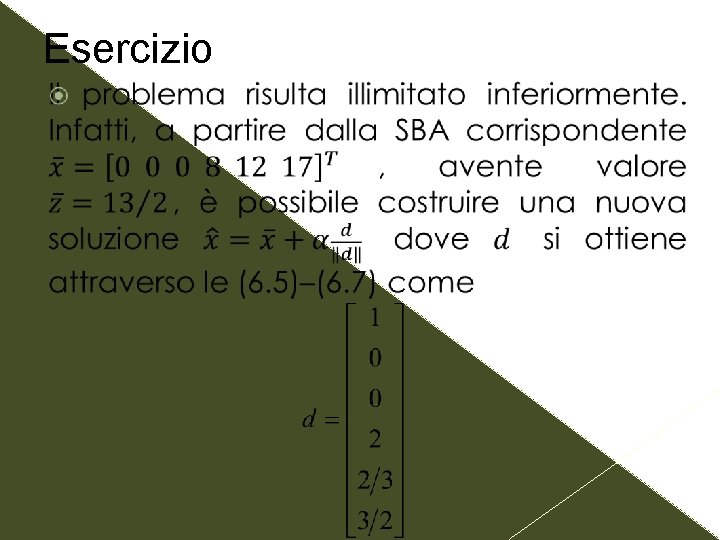
Esercizio

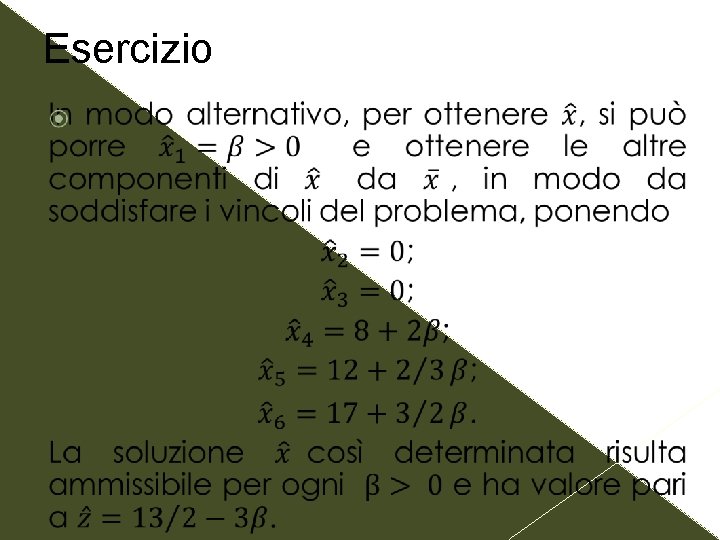
Esercizio

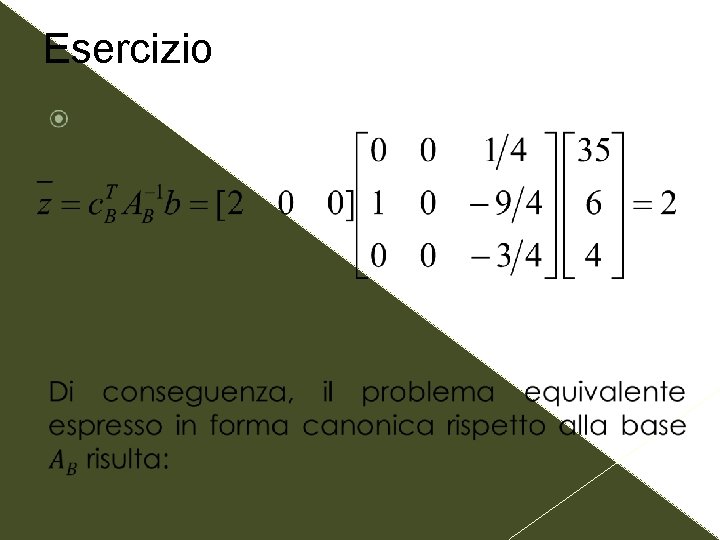
Esercizio

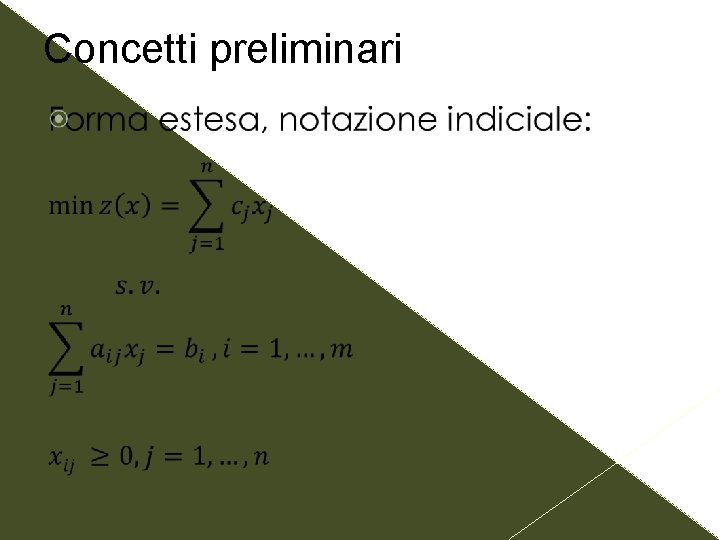
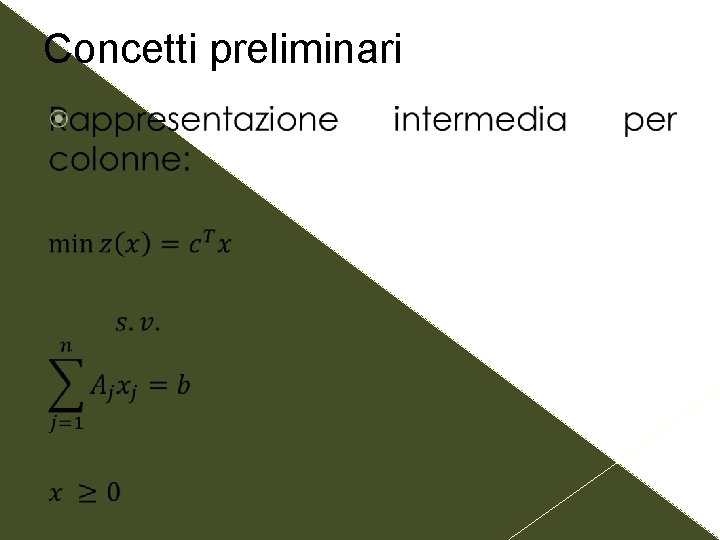
Concetti preliminari Un problema di PL è in «forma standard» se: 1. la funzione obiettivo è di minimo; 2. il poliedro P è in forma standard. Si possono utilizzare diverse notazioni per rappresentare un problema di PL in forma standard, tutte equivalenti e intercambiabili.

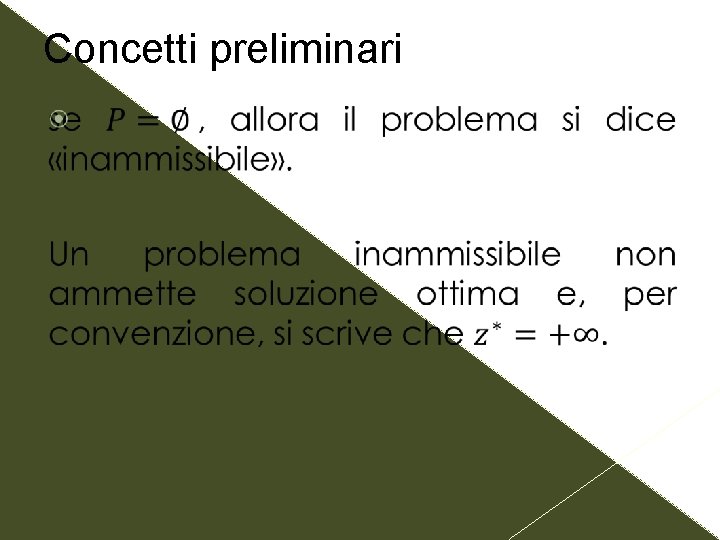
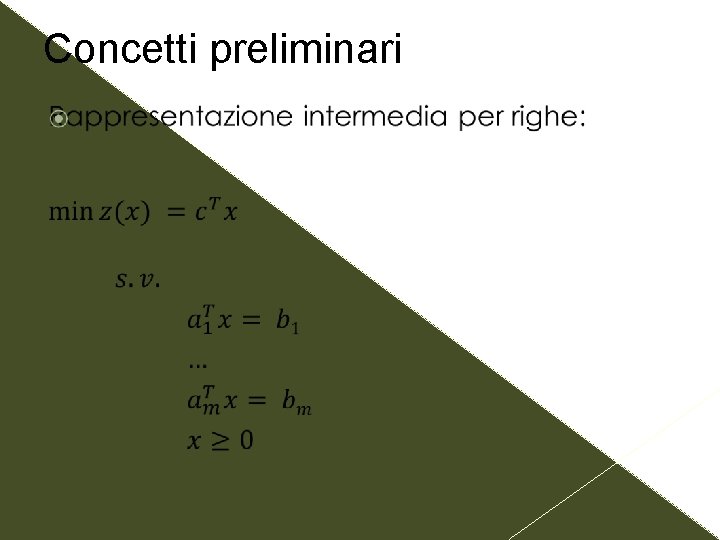
Concetti preliminari

Concetti preliminari

Concetti preliminari

Concetti preliminari

Concetti preliminari

Argomenti Concetti preliminari Condizioni geometriche di ottimalità e illimitatezza Condizioni algebriche di ottimalità

Condizioni geometriche di ottimalità e illimitatezza

Esercizio

Esercizio

Esercizio

Condizioni geometriche di ottimalità e illimitatezza

Condizioni geometriche di ottimalità e illimitatezza

Condizioni geometriche di ottimalità e illimitatezza

Condizioni geometriche di ottimalità e illimitatezza

Condizioni geometriche di ottimalità e illimitatezza

Condizioni geometriche di ottimalità e illimitatezza Ricordando il Teorema 5. 5, dal Teorema 6. 1 si deduce immediatamente che se un problema di PL è espresso in forma standard, l’esistenza di una soluzione ottima implica l’esistenza di un vertice ottimo. Inoltre, il Teorema 3. 6 fornisce uno strumento operativo per identificare i vertici di un poliedro. Si può quindi concludere introducendo il seguente corollario (6. 1).

Condizioni geometriche di ottimalità e illimitatezza

Argomenti Concetti preliminari Condizioni geometriche di ottimalità e illimitatezza Condizioni algebriche di ottimalità

Condizioni algebriche di ottimalità

Condizioni algebriche di ottimalità

Condizioni algebriche di ottimalità

Condizioni algebriche di ottimalità

Condizioni algebriche di ottimalità

Esercizio

Esercizio

Esercizio

Esercizio

Esercizio

Esercizio

Condizioni algebriche di ottimalità

Condizioni algebriche di ottimalità

Condizioni algebriche di ottimalità

Condizioni algebriche di ottimalità

Esercizio

Esercizio

Esercizio

Esercizio

Condizioni algebriche di ottimalità

Condizioni algebriche di ottimalità

Condizioni algebriche di ottimalità

Condizioni algebriche di ottimalità

Condizioni algebriche di ottimalità

Esercizio

Esercizio

Esercizio

Esercizio

Esercizio

Esercizio

Esercizio

Esercizio

Esercizio

Condizioni algebriche di ottimalità

Condizioni algebriche di ottimalità

Esercizio

Esercizio

Esercizio

Condizioni algebriche di ottimalità I risultati teorici fin qui conseguiti consentono di definire una possibile strategia per risolvere un problema di PL: si può costruire la forma canonica del problema rispetto a tutte le basi ammissibili e verificare l’eventuale soddisfacimento della condizione di ottimalità espressa dal Teorema 6. 2 o quella di illimitatezza espressa dal Teorema 6. 3. Se esiste almeno una base ammissibile, è evidente che, al termine della procedura, essendo il numero delle basi ammissibili finito, si giungerà a una delle due condizioni su indicate.

Condizioni algebriche di ottimalità
 Teoria della programmazione lineare
Teoria della programmazione lineare Ricerca operativa mappa concettuale
Ricerca operativa mappa concettuale Ricerca operativa prima guerra mondiale
Ricerca operativa prima guerra mondiale Modelli di programmazione lineare
Modelli di programmazione lineare Language acquisition and language learning
Language acquisition and language learning La coccinella rossella
La coccinella rossella L'oggetto della ricerca educativa è:
L'oggetto della ricerca educativa è: Metodologia della ricerca psicosociale
Metodologia della ricerca psicosociale Cultura della ricerca e pedagogia
Cultura della ricerca e pedagogia Metodologia della ricerca in educazione e formazione
Metodologia della ricerca in educazione e formazione Metodologia della ricerca infermieristica
Metodologia della ricerca infermieristica Fasi ricerca mialaret
Fasi ricerca mialaret Metodologia della ricerca sociale ecampus
Metodologia della ricerca sociale ecampus Quasi esperimenti
Quasi esperimenti Vertical
Vertical Etapa preoperacional piaget
Etapa preoperacional piaget Exa unne
Exa unne Disciplina operativa pemex
Disciplina operativa pemex Higiene operativa
Higiene operativa 4 fases de la administracion
4 fases de la administracion Fase operativa de la investigación
Fase operativa de la investigación Razones o indicadores financieros
Razones o indicadores financieros Investigacion operativa
Investigacion operativa Factibilidad operativa
Factibilidad operativa Articulo 13
Articulo 13 Indicadores financieros nif
Indicadores financieros nif Vision operativa
Vision operativa Efficienza operativa
Efficienza operativa Procura temprana
Procura temprana Consultoria operativa
Consultoria operativa Teoria della scelta razionale
Teoria della scelta razionale Teoria del legame di valenza zanichelli
Teoria del legame di valenza zanichelli Teoria della pertinenza sperber e wilson
Teoria della pertinenza sperber e wilson Teoria bifattoriale della regolazione delle emozioni
Teoria bifattoriale della regolazione delle emozioni Teoria della dominanza sociale
Teoria della dominanza sociale Teoria e storia della traduzione
Teoria e storia della traduzione Teoria della pace democratica
Teoria della pace democratica Teoria della nave
Teoria della nave Curva di riscaldamento dell'acqua zanichelli
Curva di riscaldamento dell'acqua zanichelli Fayol teoria della direzione amministrativa
Fayol teoria della direzione amministrativa Deutsch e gerard
Deutsch e gerard Legge di weber
Legge di weber Funzione conativa
Funzione conativa Teoria quantitativa della moneta
Teoria quantitativa della moneta Teoria atomica della materia
Teoria atomica della materia Teoria della processabilità pienemann
Teoria della processabilità pienemann Teoria conoscenza aristotele
Teoria conoscenza aristotele Teoria della processabilità pienemann
Teoria della processabilità pienemann Teoria della lubrificazione
Teoria della lubrificazione Problema thog
Problema thog Legge di proust
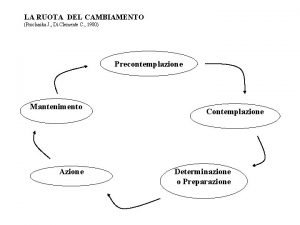
Legge di proust Prochaska di clemente
Prochaska di clemente Materia
Materia Teoria della detezione del segnale
Teoria della detezione del segnale La teoria cinetico-molecolare della materia zanichelli
La teoria cinetico-molecolare della materia zanichelli Programmazione midi
Programmazione midi Strumenti di programmazione del comune
Strumenti di programmazione del comune Programmazione e controllo arcari
Programmazione e controllo arcari Ambienti di programmazione per il software di base
Ambienti di programmazione per il software di base Paradigmi di programmazione
Paradigmi di programmazione Programmazione orientata agli oggetti
Programmazione orientata agli oggetti Programmazione concorrente e distribuita
Programmazione concorrente e distribuita Incapsulamento ereditarietà polimorfismo
Incapsulamento ereditarietà polimorfismo Sottostruttura ottima
Sottostruttura ottima Programmazione concorrente
Programmazione concorrente Strumenti compilazione/programmazione
Strumenti compilazione/programmazione Programmazione procedurale
Programmazione procedurale Programmazione allenamento minivolley
Programmazione allenamento minivolley Programmazione reticolare
Programmazione reticolare Programmazione awl
Programmazione awl Programmazione religione scuola infanzia 2019-2020
Programmazione religione scuola infanzia 2019-2020 Programmazione cnc simulator
Programmazione cnc simulator Cruciverba laurea esempio
Cruciverba laurea esempio