Algebra lineare G Puppo Algebra lineare z Numero

Algebra lineare G. Puppo

Algebra lineare z. Numero di condizionamento z. Sistemi triangolari z. Fattorizzazione LU z. Soluzione di sistemi lineari in Matlab z. Effetto del numero di condizionamento

Numero di condizionamento z. Per calcolare il numero di condizionamento, Matlab usa l’istruzione cond(a, p), dove: zp = 1 è per la norma 1 zp = 2 è per la norma 2 (default) zp = inf è per la norma infinito

Andamento del numero di condizionamento Costruiamo un programma che calcoli il numero di condizionamento al variare di N per matrici N per N assegnate. In particolare il programma deve: z avere un ciclo su N z calcolare le matrici richieste per ogni N z calcolare il numero di condizionamento corrispondente per ogni matrice, in ognuna delle norme 1, 2 e inf z stampare un grafico con i risultati

function plot_con(nmax) %Calcola il numero di condizionamento per le matrici %RAND(N), con N=1: NMAX, confrontando su un grafico %i risultati ottenuti in norma 1, norma 2, e norma inf for n=1: nmax a=rand(n); con 1(n) = cond(a, 1); con 2(n) = cond(a, 2); coninf(n) = cond(a, inf); end plot(log 10(con 2)) hold on plot(log 10(con 1), 'g') plot(log 10(coninf), 'm')(log 10(
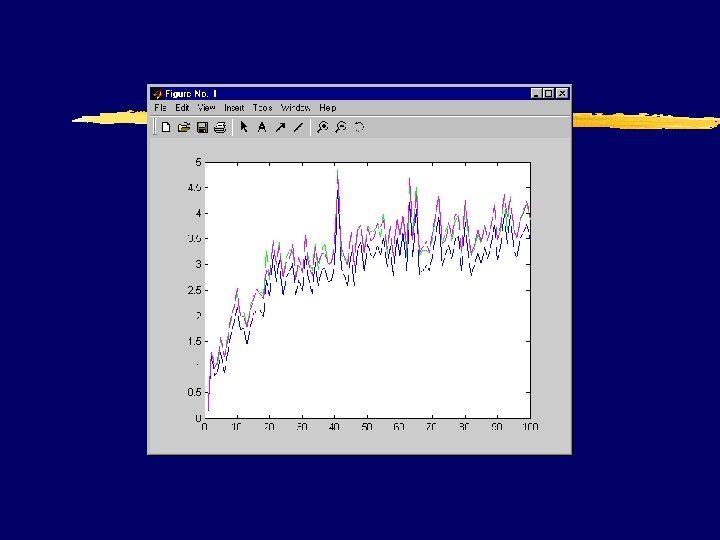

Proviamo altre matrici. . . z. Cambiamo le matrici calcolate nella function plot_con z. Sostituiamo a rand(n) le matrici tridiagonali, fornite dalla function tridiag(n) z. Sostituiamo le matrici di Hilbert, hilb(n), che hanno un condizionamento ~exp(n).
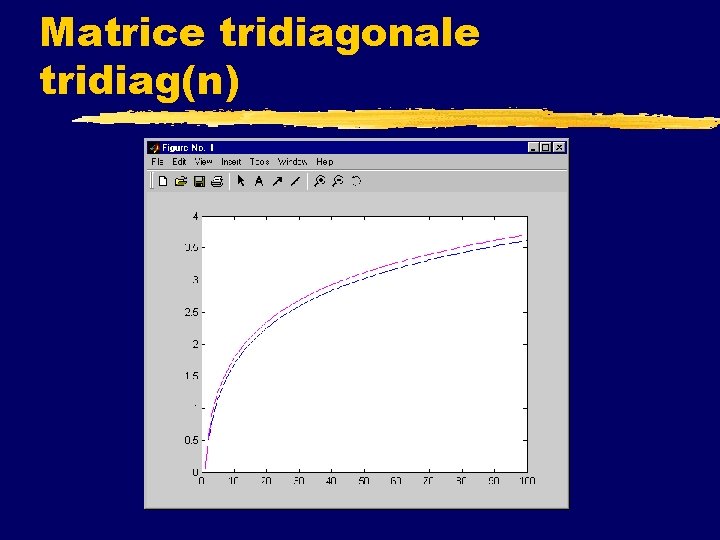
Matrice tridiagonale tridiag(n)

Matrici di Hilbert La scala verticale è logaritmica

Sistemi triangolari inferiori Scrivo una function che calcola la soluzione del sistema Ax=b, nel caso in cui A è triangolare inferiore. In una function che deve essere utilizzata da diversi utenti è bene controllare che i dati forniti siano coerenti. In questo caso controllo che: - A sia quadrata - A sia triangolare inferiore - A sia non singolare - Il vettore b abbia le dimensioni giuste

Controllo che la matrice A sia ben impostata function x=tri_inf(a, b) %TRI_INF(A, B) Risolve il sistema triangolare inferiore AX=B. % Se A non e' quadrata, o A non e' triangolare inferiore, % stampa un messaggio di errore % Controlla le dimensioni di A: [n, m] = size(a); if m ~= n display('A non e'' quadrata') return end for i=1: n for j=(i+1): n if a(i, j) ~=0 display('A non e'' triangolare inf') return end end

Termino il controllo dei dati % Controlla le dimensioni di B if length(b) ~= n display('B non e'' compatibile') return end % Controlla se A e' singolare: for i=1: n if abs( a(i, i)) < eps*norm(b) display('A e'' quasi singolare') return end

Finalmente, risolvo il sistema: La formula ricorsiva è: L’algoritmo corrispondente è: %Risolve il sistema x(1) = b(1)/a(1, 1); for i=2: n sum=b(i); for j=1: (i-1) sum = sum - a(i, j)*x(j); end x(i) = sum/a(i, i); end

Risolvo un sistema triangolare superiore. Controllo che A sia ben impostata: function x=tri_sup(a, b) %TRI_SUP(A, B) Risolve il sistema triangolare superiore AX=B. % Se A non e' quadrata, o A non e' triangolare superiore, % stampa un messaggio di errore % Controlla le dimensioni di A: [n, m] = size(a); if m ~= n display('A non e'' quadrata') return end for i=1: n for j=1: i-1 if a(i, j) ~=0 display('A non e'' triangolare sup') return end end

Controllo che B sia compatibile e che A non sia singolare % Controlla le dimensioni di B if length(b) ~= n display('B non e'' compatibile') return end % Controlla se A e' singolare: for i=1: n if abs( a(i, i)) < eps*norm(b) display('A e'' quasi singolare') return end

Risolvo il sistema: La formula ricorsiva è: E l’algoritmo corrispondente è: %Risolve il sistema x(n) = b(n)/a(n, n); for i=n-1: 1 sum=b(i); for j=i+1: n sum = sum - a(i, j)*x(j); end x(i) = sum/a(i, i); end
![Calcola la fattorizzazione LU di una matrice function [l, u] = elleu(a) %ELLEU(A) Calcola Calcola la fattorizzazione LU di una matrice function [l, u] = elleu(a) %ELLEU(A) Calcola](http://slidetodoc.com/presentation_image_h/afb60e9686733b4cec1861f6538c3e6c/image-17.jpg)
Calcola la fattorizzazione LU di una matrice function [l, u] = elleu(a) %ELLEU(A) Calcola la fattorizzazione LU di A, senza pivoting %Sintassi: [L, U]=ELLEU(A) % esce con un messaggio di errore, se trova un pivot < % EPS*NORM(A) nor=norm(a); % Controlla le dimensioni di A: [n, m] = size(a); if m ~= n display('A non e'' quadrata') return end

Calcola la fattorizzazione LU, riscrivendo su A: l=-eye(n); for k=1: n-1 if abs(a(k, k)) < eps*nor display('Pivot troppo piccolo') return end m(k+1: n, k) = -a(k+1: n, k)/a(k, k); a(k+1: n, k+1: n) = a(k+1: n, k+1: n)+m(k+1: n, k)*a(k, k+1: n); end

…infine, immagazzina i risultati nelle matrici L e U: % Immagazzina i risultati nelle matrici l e u: l = -m; u = zeros(n); for i=1: n for j=i: n u(i, j) = a(i, j); end

Risoluzione di un sistema lineare Con le tre functions appena costruite, posso risolvere un sistema lineare. Devo impostare una matrice quadrata A e un vettore B di termini noti. Per risolvere il sistema Ax=B, devo: z Calcolare la fattorizzazione LU; z Risolvere il sistema triangolare inferiore Ly=b; z Risolvere il sistema triangolare superiore Ux=y; >> [l, u]=elleu(a); >> y=tri_inf(l, b); >> x=tri_sup(u, y)

Esempio Risolvo il sistema Ax=b, per: >> a=[2 -1 0; -1 2 -1; 0 -1 2]; >> a a= 2 -1 0 -1 2 >> b=ones(3, 1);
![Calcola la fattorizzazione LU: >> [l, u]=elleu(a) l= 1. 0000 0 0 -0. 5000 Calcola la fattorizzazione LU: >> [l, u]=elleu(a) l= 1. 0000 0 0 -0. 5000](http://slidetodoc.com/presentation_image_h/afb60e9686733b4cec1861f6538c3e6c/image-22.jpg)
Calcola la fattorizzazione LU: >> [l, u]=elleu(a) l= 1. 0000 0 0 -0. 5000 1. 0000 0 0 -0. 6667 1. 0000 u= 2. 0000 -1. 0000 0 0 1. 5000 -1. 0000 0 0 1. 3333 Osservo che: >> l*u ans = 2 -1 -1 2 0 -1 2

Risolvo i due sistemi triangolari >> y=tri_inf(l, b) y= 1. 0000 1. 5000 >> x=tri_sup(u, y) x= 1. 5000 2. 0000 1. 5000 Osservo che >> a*x'-b ans = 1. 0 e-015 * 0 0. 2220 -0. 4441 Quindi, il residuo è piccolo, anche se non è zero. La soluzione è accettabile

Provo un altro esempio con a=hilb(5), b=ones(5, 1). Ottengo: >> a=hilb(5); >> b=ones(5, 1); >> [l, u]=elleu(a); >> y=tri_inf(l, b); >> x=tri_sup(u, y); >> norm(a*x'-b) ans = 3. 1776 e-014 Quindi il residuo è aumentato, infatti: >> cond(a) ans = 4. 7661 e+005

L’effetto del numero di condizionamento si vede meglio con questo esempio: Scelgo b, in modo da conoscere la soluzione esatta, x. Calcolo la soluzione x 1 risolvendo il sistema lineare. In aritmetica esatta, avrei x-x 1=0. In aritmetica floating point: >> a=hilb(5); >> x=ones(5, 1); >> b=a*x; >> [l, u]=elleu(a); >> y=tri_inf(l, b); >> x 1=tri_sup(u, y); >> norm(x-x 1')/norm(x) ans = 1. 5531 e-012 La differenza ||x-x 1|| è molto più grande del residuo

Risoluzione di sistemi lineari con Matlab risolve il sistema lineare Ax=b con il comando: x=Ab. Se A è quadrata, questo comando implica i seguenti passi: - Calcola la fattorizzazione LU con pivoting sulle colonne - Risolvi i due sistemi triangolari Se A è rettangolare (sistemi sovradeterminati), Matlab calcola la soluzione nel senso dei minimi quadrati, cioè: - Calcola la fattorizzazione QR con pivoting sulle colonne - Risolve il sistema triangolare superiore Se il condizionamento di A è elevato, stampa un messaggio di warning, ma calcola ugualmente la soluzione.

Risoluzione di sistemi lineari con Matlab 2 Nella versione 7, è stata inserita una nuova function per risolvere sistemi lineari con struttura particolare x=linsolve(a, b)
![Esempio >> a=[2 -1 0; -1 2 -1; 0 -1 2]; >> b=ones(3, 1); Esempio >> a=[2 -1 0; -1 2 -1; 0 -1 2]; >> b=ones(3, 1);](http://slidetodoc.com/presentation_image_h/afb60e9686733b4cec1861f6538c3e6c/image-28.jpg)
Esempio >> a=[2 -1 0; -1 2 -1; 0 -1 2]; >> b=ones(3, 1); >> x=ab x= 1. 5000 2. 0000 1. 5000 Attenzione! Matlab usa sia / che ma i due operatori hanno un effetto diverso. Provare per credere!

Attenzione! Matlab calcola una soluzione anche quando il sistema non ammette soluzione. Nell’esempio seguente, a è singolare: >> a=[1 2 3; 4 5 6; 7 8 9]; >> b=[1; 1; 0]; >> x=ab; Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 1. 541976 e-018. >> norm(a*x-b) ans = 5. 0990 RCOND è il reciproco del numero di condizionamento: se RCOND è piccolo, la matrice è mal condizionata.

Fattorizzazione LU Matlab calcola la fattorizzazione LU di una matrice con il comando: [l, u] = lu(a) In questo caso, l contiene anche gli scambi di riga effettuati. Se la fattorizzazione è PA = LU, allora l=P-1 L. Oppure posso usare tre argomenti in output: : [l, u, p]=lu(a) In questo caso, l=L, u=U, p=P.
![Esempio >> a=[1 2 3; 4 5 6; 7 8 9]; >> [l, u]=lu(a) Esempio >> a=[1 2 3; 4 5 6; 7 8 9]; >> [l, u]=lu(a)](http://slidetodoc.com/presentation_image_h/afb60e9686733b4cec1861f6538c3e6c/image-31.jpg)
Esempio >> a=[1 2 3; 4 5 6; 7 8 9]; >> [l, u]=lu(a) l= 0. 1429 1. 0000 0 0. 5714 0. 5000 1. 0000 0 0 u= 7. 0000 8. 0000 9. 0000 0 0. 8571 1. 7143 0 0 0. 0000 Notare che l contiene la matrice triangolare L con le righe scambiate, cioè l=P-1 L

Per forzare la soluzione di un sistema tramite fattorizzazione LU, devo quindi dare i comandi: >> [l, u]=lu(a); >> y=lb; >> x=uy;
![Fattorizzazione QR Matlab esegue la fattorizzazione A=QR mediante il comando: >>[q, r] = qr(a) Fattorizzazione QR Matlab esegue la fattorizzazione A=QR mediante il comando: >>[q, r] = qr(a)](http://slidetodoc.com/presentation_image_h/afb60e9686733b4cec1861f6538c3e6c/image-33.jpg)
Fattorizzazione QR Matlab esegue la fattorizzazione A=QR mediante il comando: >>[q, r] = qr(a) Per forzare la soluzione di un sistema lineare mediante fattorizzazione QR devo quindi dare i comandi: >> [q, r]=qr(a); >> x=rq'*b;

Esercizio

Effetto del numero di condizionamento z. Variazione del residuo per matrici mal condizionate z. Effetto del condizionamento sulla precisione della soluzione numerica z. Stima del rango

Variazione del residuo per matrici mal condizionate Scrivo un programma che calcoli, per n da 1 a 100: -Vorrei a=hilb(n) studiare come varia il residuo -r b=rand(n, 1) = ||Ax-b||, in funzione del condizionamento - risolve il sistema a*x=b della matrice A. Scelgo come matrice mal - calcola la norma del residuo a*x-b condizionata la matrice di Hilbert, mentre per - calcola il condizionamento di a b- stampa assegno vettore numeri casualied il residuo un un grafico con ildicondizionamento in funzione di n

Script res_hilb. m %Esegue un grafico del residuo, in funzione di n, %per sistemi lineari del tipo Hilb(n)*x=rand(n, 1) nmax=100; for n=1: nmax a=hilb(n); b=rand(n, 1); x=ab; c(n)=cond(a); r(n)=norm(a*x-b) end plot(log 10(c)) hold on plot(log 10(r+eps), 'm')
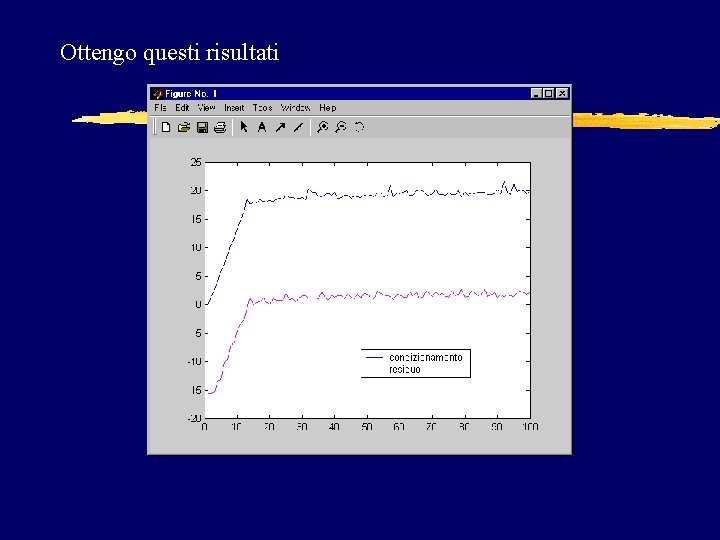
Ottengo questi risultati

Effetto del condizionamento sulla precisione della soluzione Scrivo un programma che calcoli, per n da 1 a 100: - a=hilb(n) Imposto un problema Ax=b di cui conosco la - xexa=ones(n, 1) (xexa=soluzione esatta) soluzione esatta. numericamente il - b=a*xexa (b =Risolvo termine noto corrispondente a xexa) - risolve il calcolando sistema a*x=b la (x=soluzione approssimata) problema, soluzione stimata y. - calcola l’errore relativo fra||x-y||. x e xexa Quindi calcolo - calcola il condizionamento di a Mi -aspetto se uso per e. Al’errore una stampa unerrori grafico grandi con il condizionamento relativo matrice mal condizionata, come, di nuovo, la matrice di Hilbert.

Script hilb_exa. m % Calcola la differenza fra soluzione esatta e soluzione % approssimata, per i sistemi lineari hilb(n)*x=b % e ne stampa il grafico, confrontando con il condizionamento nmax=100; for n=1: nmax a=hilb(n); xexa=ones(n, 1); b=a*xexa; x=ab; c(n)=cond(a); err(n)=norm(x-xexa)/norm(xexa); end plot(log 10(c)) hold on plot(log 10(err+eps), 'm')
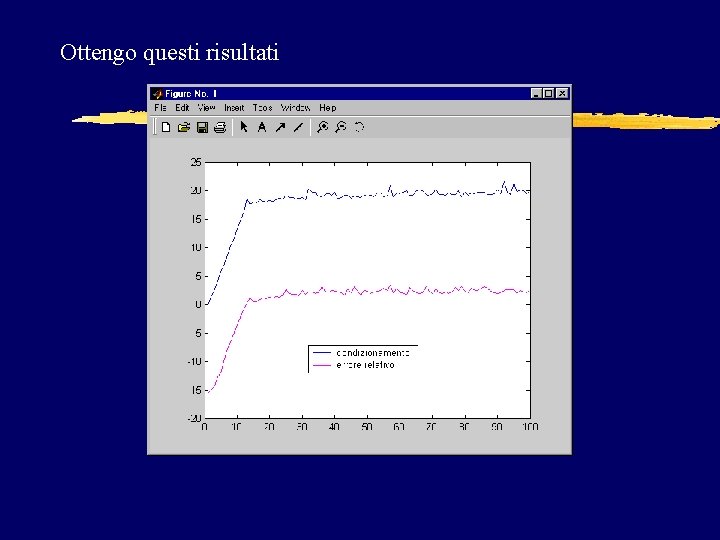
Ottengo questi risultati

Stima del rango di una matrice Per stimare il rango di una matrice posso: z Calcolare la fattorizzazione LU e contare gli elementi U(i, i) che hanno modulo maggiore di una tolleranza assegnata z Calcolare la fattorizzazione QR e contare gli elementi R(i, i) che hanno modulo maggiore di una tolleranza assegnata Per matrici mal condizionate il secondo metodo è più affidabile. La tolleranza assegnata ha un ruolo fondamentale

Listato della function rango. m function r=rango(a, tol) % Calcola il rango della matrice A, usando % il metodo QR % Sintassi: R=RANGO(A) Calcola il rango di A. Usa EPS % se |r(i, i)| <EPS*norm(a, 1) => r(i, i)=0 % R=RANGO(A, TOL) Calcola il rango di A, % se |r(i, i)| <TOL => r(i, i)=0 Questa function può essere chiamata in due modi: rango(a) usa una tolleranza di default: TOL=EPS*NORM(a, 1) rango(a, tol) usa la tolleranza TOL fissata in input

Questa possibilità di scelta è implementata con la function NARGIN, che conta il numero di argomenti in input: if nargin < 2 tol=eps*norm(a, 1); end Quindi, se NARGIN ritorna il valore 1, la function RANGO calcola la tolleranza, TOL=EPS*NORM(A, 1) altrimenti TOL non viene calcolata, ma viene usato il valore assegnato in input

function r=rango(a, tol) % Calcola il rango della matrice A, usando % il metodo QR % Sintassi: R=RANGO(A) Calcola il rango di A. Usa EPS % se |r(i, i)| <EPS*norm(a, 1) => r(i, i)=0 % R=RANGO(A, TOL) Calcola il rango di A, % se |r(i, i)| <TOL => r(i, i)=0 if nargin < 2 tol=eps*norm(a, 1); end [q, rr]=qr(a); r=0; [m, n]=size(a); for i=1: n if abs(rr(i, i))>tol r=r+1; end

Provo ora a calcolare il rango delle matrici di Hilbert. Uso le seguenti istruzioni: for i=1: 100 r(i)=rango(hilb(i)); end >> plot(r) Notare che tutte le matrici di Hilbert sono non singolari, quindi dovrei avere r(i)=i
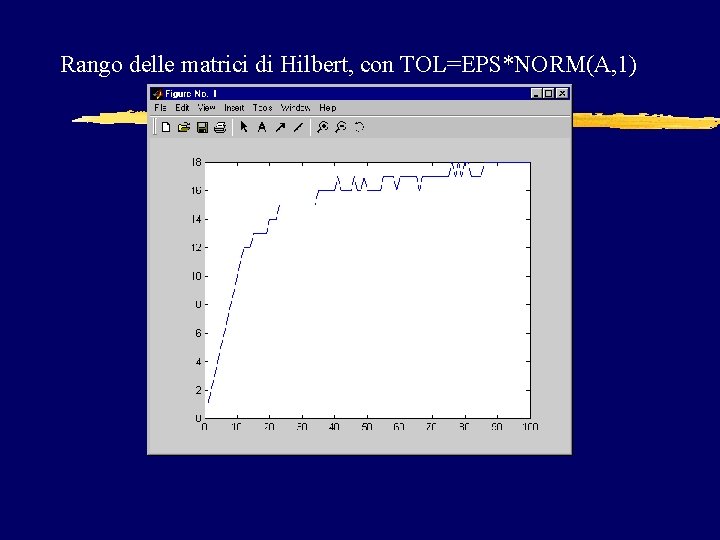
Rango delle matrici di Hilbert, con TOL=EPS*NORM(A, 1)
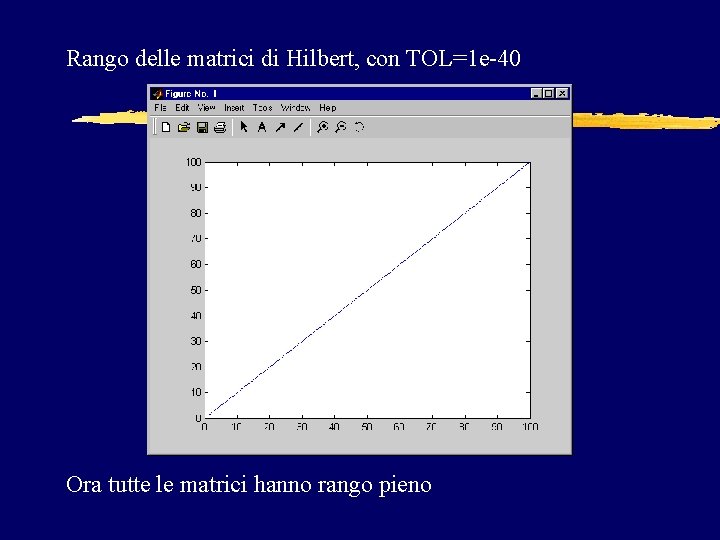
Rango delle matrici di Hilbert, con TOL=1 e-40 Ora tutte le matrici hanno rango pieno

Apparentemente, i risultati ottenuti con TOL=1 e-40 sono più corretti di quelli ottenuti con TOL=EPS*NORM(A, 1). Calcoliamo però qual è l’accuratezza della fattorizzazione QR che stiamo calcolando, per esempio per HILB(50): >> a=hilb(50); >> [q, r]=qr(a); >> norm(q*r-a) ans = 5. 7905 e-016 Quindi non ha senso usare un valore di TOL più basso di circa 1 e-16, perché la matrice R non è abbastanza accurata
- Slides: 49