STAT 497 LECTURE NOTES 3 STATIONARY TIME SERIES

STAT 497 LECTURE NOTES 3 STATIONARY TIME SERIES PROCESSES (ARMA PROCESSES OR BOX-JENKINS PROCESSES) 1

AUTOREGRESSIVE PROCESSES • AR(p) PROCESS: or where 2

AR(p) PROCESS • Because the process is always invertible. • To be stationary, the roots of p(B)=0 must lie outside the unit circle. • The AR process is useful in describing situations in which the present value of a time series depends on its preceding values plus a random shock. 3

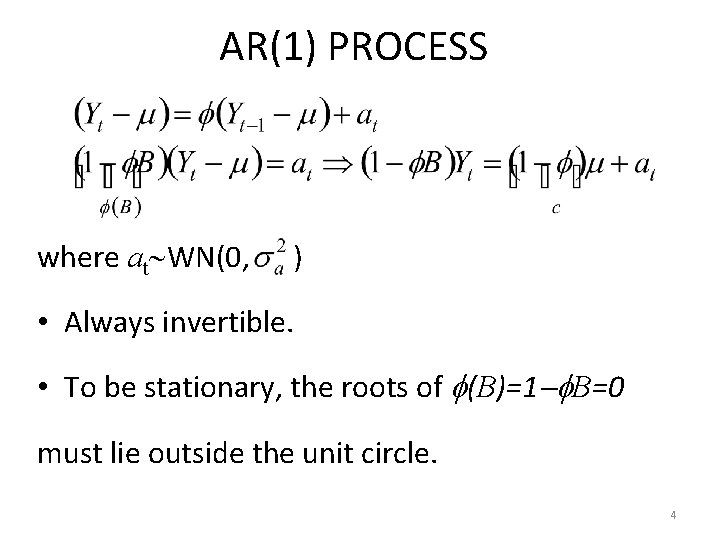
AR(1) PROCESS where at WN(0, ) • Always invertible. • To be stationary, the roots of (B)=1 B=0 must lie outside the unit circle. 4

AR(1) PROCESS • OR using the characteristic equation, the roots of m =0 must lie inside the unit circle. B= 1 |B|<| 1| | |<1 STATIONARITY CONDITION 5

AR(1) PROCESS • This process sometimes called as the Markov process because the distribution of Yt given Yt 1, Yt 2, … is exactly the same as the distribution of Yt given Yt 1. 6

AR(1) PROCESS • PROCESS MEAN: 7

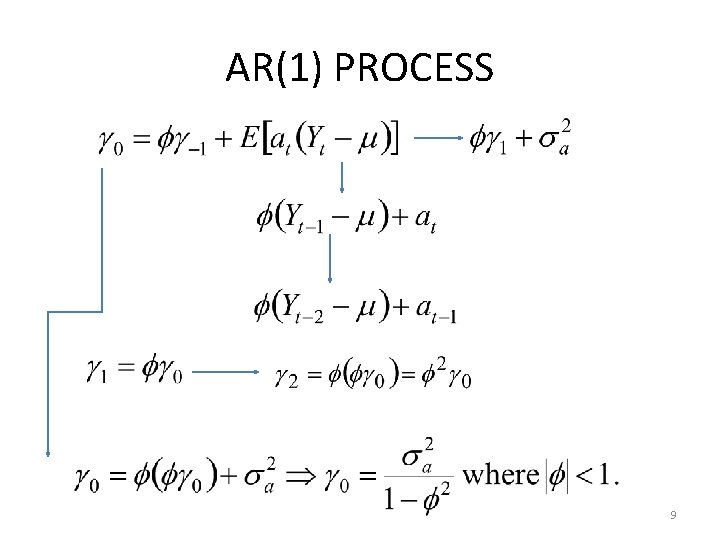
AR(1) PROCESS • AUTOCOVARIANCE FUNCTION: k Keep this part as it is 8

AR(1) PROCESS 9

AR(1) PROCESS When | |<1, the process is stationary and the ACF decays exponentially. 10

AR(1) PROCESS • 0 < < 1 All autocorrelations are positive. • 1 < < 0 The sign of the autocorrelation shows an alternating pattern beginning a negative value. 11

AR(1) PROCESS • RSF: Using the geometric series 12

AR(1) PROCESS • RSF: By operator method _ We know that 13

AR(1) PROCESS • RSF: By recursion 14

THE SECOND ORDER AUTOREGRESSIVE PROCESS • AR(2) PROCESS: Consider the series satisfying where at WN(0, ). 15

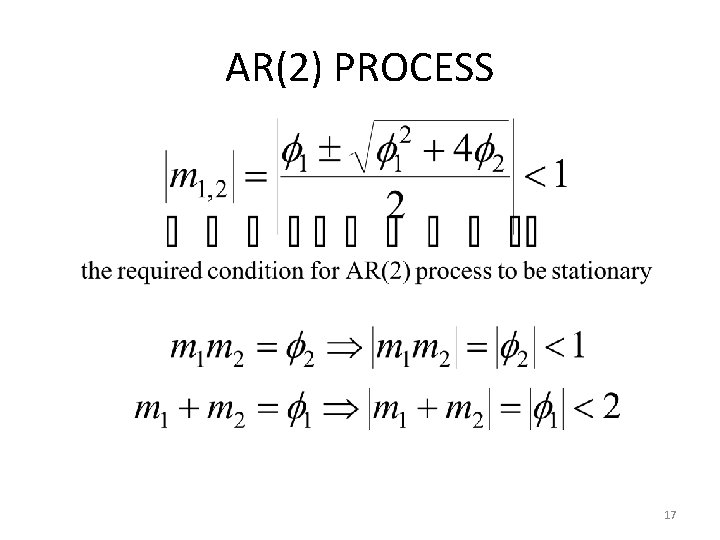
AR(2) PROCESS • Always invertible. • Already in the Inverted Form. • To be stationary, the roots of must lie outside the unit circle. OR the roots of the characteristic equation must lie inside the unit circle. 16

AR(2) PROCESS 17

AR(2) PROCESS • Considering both real and complex roots, we have the following stationary conditions for AR(2) process (see page 84 for the proof) 18

AR(2) PROCESS • THE AUTOCOVARIANCE FUNCTION: Assuming stationarity and that at is independent of Yt k, we have 19

AR(2) PROCESS 20

AR(2) PROCESS 21

AR(2) PROCESS 22

AR(2) PROCESS 23

AR(2) PROCESS ACF: It is known as Yule-Walker Equations ACF shows an exponential decay or sinusoidal behavior. 24

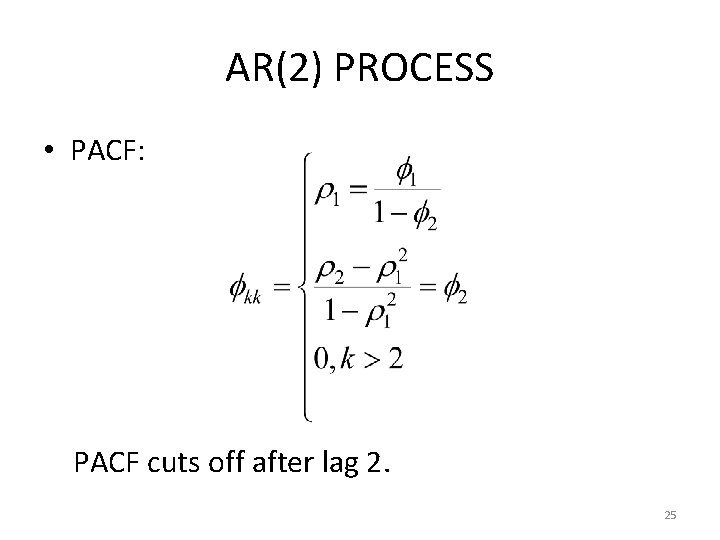
AR(2) PROCESS • PACF: PACF cuts off after lag 2. 25

AR(2) PROCESS • RANDOM SHOCK FORM: Using the Operator Method 26

The p-th ORDER AUTOREGRESSIVE PROCESS: AR(p) PROCESS • Consider the process satisfying where at WN(0, ). provided that roots of all lie outside the unit circle 27

AR(p) PROCESS • ACF: Yule-Walker Equations • ACF: tails of as a mixture of exponential decay or damped sine wave (if some roots are complex). • PACF: cuts off after lag p. 28

MOVING AVERAGE PROCESSES • Suppose you win 1 TL if a fair coin shows a head and lose 1 TL if it shows tail. Denote the outcome on toss t by at. • The average winning on the last 4 tosses=average pay-off on the last tosses: MOVING AVERAGE PROCESS 29

MOVING AVERAGE PROCESS • Errors are the average of this period’s random error and last period’s random error. • No memory of past levels. • The impact of shock to the series takes exactly 1 -period to vanish for MA(1) process. In MA(2) process, the shock takes 2 -periods and then fade away. • In MA(1) process, the correlation would last only one period. 30

MOVING AVERAGE PROCESSES • Consider the process satisfying 31

MOVING AVERAGE PROCESSES • Because , MA processes are always stationary. • Invertible if the roots of q(B)=0 all lie outside the unit circle. • It is a useful process to describe events producing an immediate effects that lasts for short period of time. 32

THE FIRST ORDER MOVING AVERAGE PROCESS_MA(1) PROCESS • Consider the process satisfying 33

MA(1) PROCESS • From autocovariance generating function 34

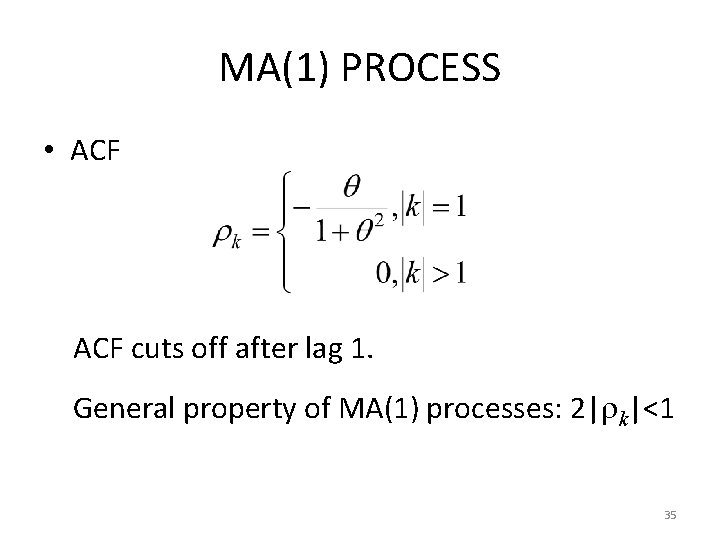
MA(1) PROCESS • ACF cuts off after lag 1. General property of MA(1) processes: 2| k|<1 35

MA(1) PROCESS • PACF: 36

MA(1) PROCESS • Basic characteristic of MA(1) Process: – ACF cuts off after lag 1. – PACF tails of exponentially depending on the sign of . – Always stationary. – Invertible if the root of 1 B=0 lie outside the unit circle or the root of the characteristic equation m =0 lie inside the unit circle. INVERTIBILITY CONDITION: | |<1. 37

MA(1) PROCESS • It is already in RSF. • IF: 1= 2= 2 38

MA(1) PROCESS • IF: By operator method 39

THE SECOND ORDER MOVING AVERAGE PROCESS_MA(2) PROCESS • Consider the moving average process of order 2: 40

MA(2) PROCESS • From autocovariance generating function 41

MA(2) PROCESS • ACF cuts off after lag 2. • PACF tails of exponentially or a damped sine waves depending on a sign and magnitude of parameters. 42

MA(2) PROCESS • Always stationary. • Invertible if the roots of all lie outside the unit circle. OR if the roots of all lie inside the unit circle. 43

MA(2) PROCESS • Invertibility condition for MA(2) process 44

MA(2) PROCESS • It is already in RSF form. • IF: Using the operator method: 45

The q-th ORDER MOVING PROCESS_ MA(q) PROCESS Consider the MA(q) process: 46

MA(q) PROCESS • The autocovariance function: • ACF: 47

THE AUTOREGRESSIVE MOVING AVERAGE PROCESSES_ARMA(p, q) PROCESSES • If we assume that the series is partly autoregressive and partly moving average, we obtain a mixed ARMA process. 48

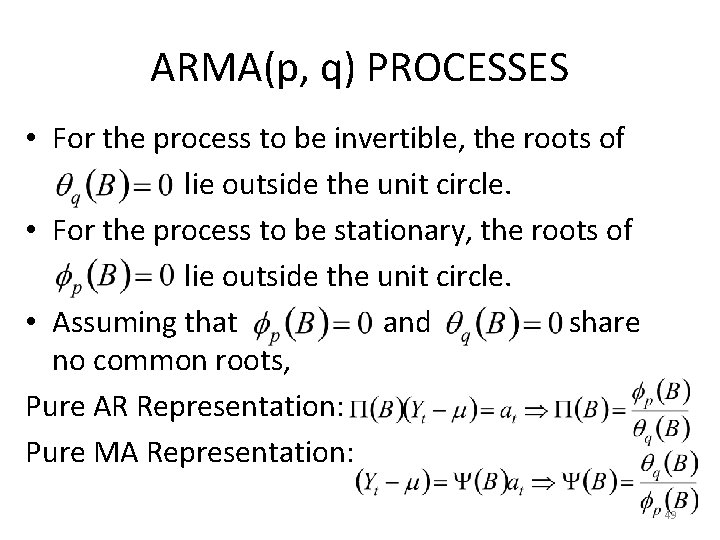
ARMA(p, q) PROCESSES • For the process to be invertible, the roots of lie outside the unit circle. • For the process to be stationary, the roots of lie outside the unit circle. • Assuming that and share no common roots, Pure AR Representation: Pure MA Representation: 49

ARMA(p, q) PROCESSES • Autocovariance function • ACF • Like AR(p) process, it tails of after lag q. • PACF: Like MA(q), it tails of after lag p. 50

ARMA(1, 1) PROCESSES • The ARMA(1, 1) process can be written as • Stationary if | |<1. • Invertible if | |<1. 51

ARMA(1, 1) PROCESSES • Autocovariance function: 52

ARMA(1, 1) PROCESS • The process variance 53

ARMA(1, 1) PROCESS 54

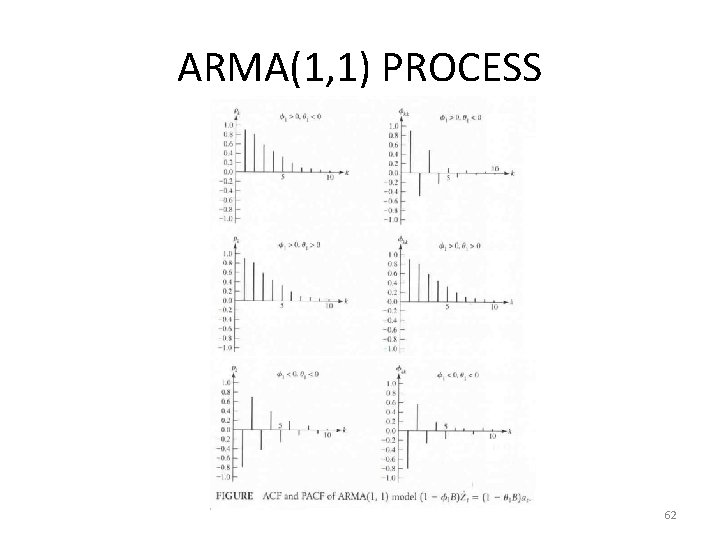
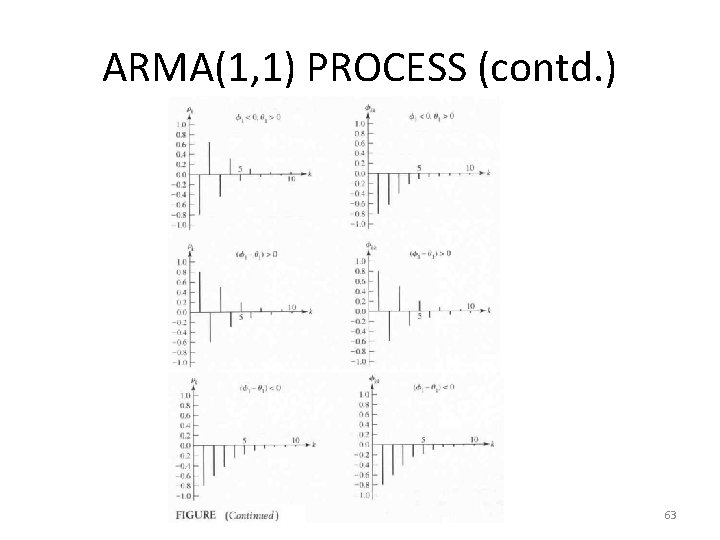
ARMA(1, 1) PROCESS • Both ACF and PACF tails of after lag 1. 55

ARMA(1, 1) PROCESS • IF: 56

ARMA(1, 1) PROCESS • RSF: 57

AR(1) PROCESS 58

AR(2) PROCESS 59

MA(1) PROCESS 60

MA(2) PROCESS 61

ARMA(1, 1) PROCESS 62

ARMA(1, 1) PROCESS (contd. ) 63