STAT 497 LECTURE NOTES 2 1 THE AUTOCOVARIANCE

























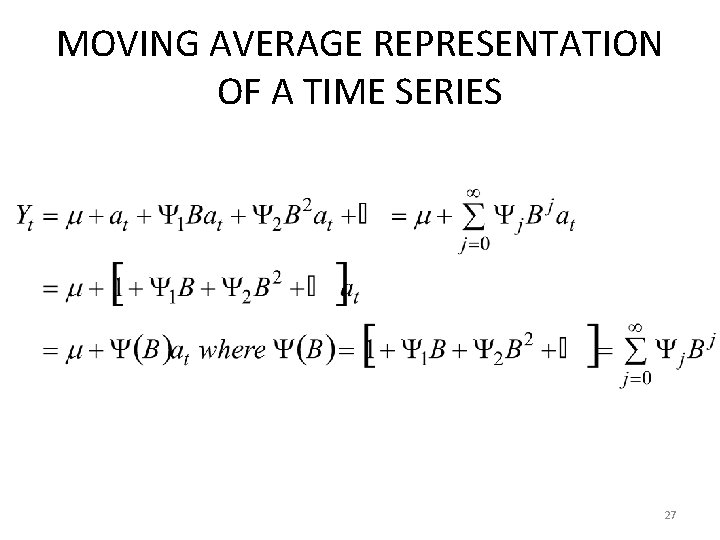















- Slides: 43

STAT 497 LECTURE NOTES 2 1

THE AUTOCOVARIANCE AND THE AUTOCORRELATION FUNCTIONS • For a stationary process {Yt}, the autocovariance between Yt and Yt-k is and the autocorrelation function is 2

THE AUTOCOVARIANCE AND THE AUTOCORRELATION FUNCTIONS PROPERTIES: 1. 2. 3. 4. (necessary condition) k and k are positive semidefinite 3 for any set of time points t 1, t 2, …, tn and any real numbers 1, 2, …, n.

THE PARTIAL AUTOCORRELATION FUNCTION (PACF) • PACF is the correlation between Yt and Yt-k after their mutual linear dependency on the intervening variables Yt-1, Yt-2, …, Yt-k+1 has been removed. • The conditional correlation is usually referred as the partial autocorrelation in time series. 4

CALCULATION OF PACF 1. REGRESSION APPROACH: Consider a model from a zero mean stationary process where ki denotes the coefficients of Yt k+i and et k is the zero mean error term which is uncorrelated with Yt k+i, i=0, 1, …, k. • Multiply both sides by Yt k+j 5

CALCULATION OF PACF and taking the expectations diving both sides by 0 PACF 6

CALCULATION OF PACF • For j=1, 2, …, k, we have the following system of equations 7

CALCULATION OF PACF • Using Cramer’s rule successively for k=1, 2, … 8

CALCULATION OF PACF 9

CALCULATION OF PACF 2. Levinson and Durbin’s Recursive Formula: 10

WHITE NOISE (WN) PROCESS • A process {at} is called a white noise (WN) process, if it is a sequence of uncorrelated random variables from a fixed distribution with constant mean {E(at)= }, constant variance {Var(at)= } and Cov(Yt, Yt-k)=0 for all k≠ 0. 11

WHITE NOISE (WN) PROCESS • It is a stationary process with autocovariance function Basic Phenomenon: ACF=PACF=0, k 0. 12

WHITE NOISE (WN) PROCESS • White noise (in spectral analysis): white light is produced in which all frequencies (i. e. , colors) are present in equal amount. • Memoryless process • Building block from which we can construct more complicated models • It plays the role of an orthogonal basis in the general vector and function analysis. 13

ESTIMATION OF THE MEAN, AUTOCOVARIANCE AND AUTOCORRELATION • THE SAMPLE MEAN: 14

ERGODICITY • In a strictly stationary or covariance stationary stochastic process no assumption is made about the strength of dependence between random variables in the sequence. However, in many contexts it is reasonable to assume that the strength of dependence between random variables in a stochastic process diminishes the farther apart they become. This diminishing dependence assumption is captured by the concept of ergodicity. 15

ERGODICITY • A process in which every sequence or sizable sample is equally representative of the whole. • Kolmogorov’s law of large number (LLN) tells that if Xi i. i. d. (μ, 2) for i = 1, . . . , n, then we have the following limit for the ensemble average • In time series, we have time series average, not ensemble average. Hence, the mean is computed by averaging over time. Does the time series average converges to the same limit as the ensemble average? The answer is yes, if Yt is stationary and ergodic. 16

ERGODICITY • The time-ensemble statistical properties are the same as the realization-ensemble statistical properties, if the process is ergodic. • A covariance stationary process is said to ergodic for the mean, if the time series average converges to the population mean. • Similarly, if the sample average provides an consistent estimate for the second moment, then the process is said to be ergodic for the second moment. 17

ERGODICITY • A sufficient condition for a covariance stationary process to be ergodic for the mean is that . Further, if the process is Gaussian, then absolute summable autocovariances also ensure that the process is ergodic for all moments. • The ergodicity plays a central role in estimations of the statistical quantities, where it ensures that time series estimates serves as unbiased estimators of the considered statistical parameters. 18

THE SAMPLE AUTOCOVARIANCE FUNCTION or 19

THE SAMPLE AUTOCORRELATION FUNCTION • A plot versus k a sample correlogram • For large sample sizes, is normally distributed with mean k and variance is approximated by Bartlett’s approximation for processes in which k=0 for k>m. 20

THE SAMPLE AUTOCORRELATION FUNCTION • In practice, i’s are unknown and replaced by their sample estimates, . Hence, we have the following large-lag standard error of : 21

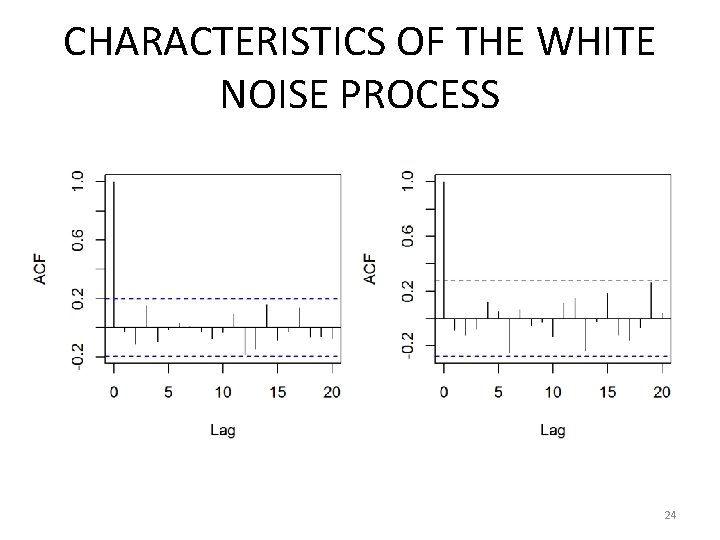
THE SAMPLE AUTOCORRELATION FUNCTION • For a WN process, we have • The ~95% confidence interval for k: For a WN process, it must be close to zero. • Hence, to test the process is WN or not, draw a 2/n 1/2 lines on the sample correlogram. If all are inside the limits, the process could be WN (we need to check the sample PACF, too). 22

THE SAMPLE PARTIAL AUTOCORRELATION FUNCTION • For a WN process, • 2/n 1/2 can be used as critical limits on kk to test the hypothesis of a WN process. 23

CHARACTERISTICS OF THE WHITE NOISE PROCESS 24

BACKSHIFT (OR LAG) OPERATORS • Backshift operator, B is defined as e. g. Random Shock Process: 25

MOVING AVERAGE REPRESENTATION OF A TIME SERIES • Also known as Random Shock Form or Wold (1938) Representation. • Let {Yt} be a time series. For a stationary process {Yt}, we can write {Yt} as a linear combination of sequence of uncorrelated (WN) r. v. s. A GENERAL LINEAR PROCESS: where 0=I, {at} is a 0 mean WN process and 26
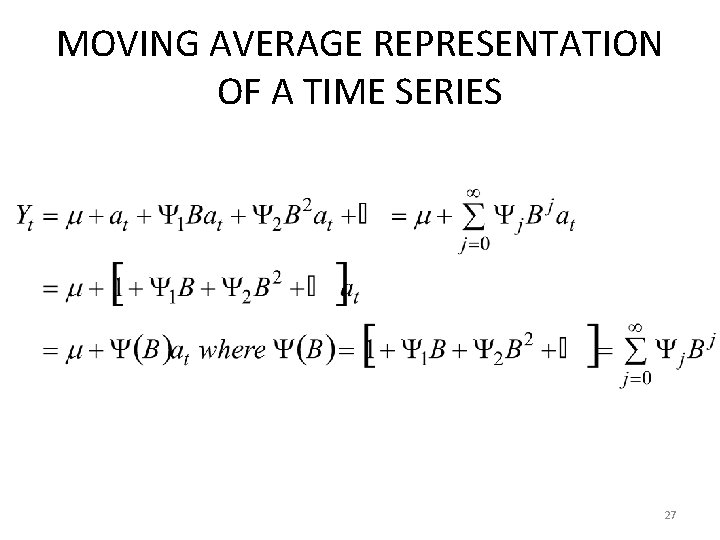
MOVING AVERAGE REPRESENTATION OF A TIME SERIES 27
MOVING AVERAGE REPRESENTATION OF A TIME SERIES 28

MOVING AVERAGE REPRESENTATION OF A TIME SERIES • Because they involve infinite sums, to be stationary • Hence, is the required condition for the process to be stationary. • It is a non-deterministic process: A process contains no deterministic components (no randomness in the future states of the system) that can be forecast exactly from its own past. 29

AUTOCOVARIANCE GENERATING FUNCTION • For a given sequence of autocovariances k, k=0, 1, 2, … the autocovariance generating function is defined as where the variance of a given process 0 is the coefficient of B 0 and the autocovariance of lag k, k is the coefficient of both Bk and B k. 2 1 30

AUTOCOVARIANCE GENERATING FUNCTION • Using and stationarity where j=0 for j<0. 31

AUTOCORRELATION GENERATING FUNCTION 32

EXAMPLE a) Write the above equation in random shock form. b) Find the autocovariance generating function. 33

AUTOREGRESSIVE REPRESENTATION OF A TIME SERIES • This representation is also known as INVERTED FORM. • Regress the value of Yt at time t on its own past plus a random shock. 34

AUTOREGRESSIVE REPRESENTATION OF A TIME SERIES • It is an invertible process (it is important forecasting). Not every stationary process is invertible (Box and Jenkins, 1978). • Invertibility provides uniqueness of the autocorrelation function. • It means that different time series models can be re-expressed by each other. 35

INVERTIBILITY RULE USING THE RANDOM SHOCK FORM • For a linear process, to be invertible, the roots of (B)=0 as a function of B must lie outside the unit circle. • If is a root of (B), then | |>1. (real number) | | is the absolute value of . (complex number) | | is 36

INVERTIBILITY RULE USING THE RANDOM SHOCK FORM • It can be stationary if the process can be rewritten in a RSF, i. e. , 37

STATIONARITY RULE USING THE INVERTED FORM • For a linear process, to be stationary, the roots of (B)=0 as a function of B must lie outside the unit circle. • If is a root of (B), then | |>1. 38

RANDOM SHOCK FORM AND INVERTED FORM • AR and MA representations are not the model form. Because they contain infinite number of parameters that are impossible to estimate from a finite number of observations. 39

TIME SERIES MODELS • In the Inverted Form of a process, if only finite number of weights are non-zero, i. e. , the process is called AR(p) process. 40

TIME SERIES MODELS • In the Random Shock Form of a process, if only finite number of weights are non-zero, i. e. , the process is called MA(q) process. 41

TIME SERIES MODELS • AR(p) Process: • MA(q) Process: 42

TIME SERIES MODELS • The number of parameters in a model can be large. A natural alternate is the mixed AR and MA process ARMA(p, q) process • For a fixed number of observations, the more parameters in a model, the less efficient is the estimation of the parameters. Choose a simpler model to describe the phenomenon. 43