Physics 111 Lecture 1 Mechanics for Physicists and

Physics 111: Lecture 1 “Mechanics for Physicists and Engineers” Agenda for Today l l Advice Scope of this course Measurement and Units çFundamental units çSystems of units çConverting between systems of units çDimensional Analysis 1 -D Kinematics (review) çAverage & instantaneous velocity and acceleration çMotion with constant acceleration Physics 111: Lecture 1, Pg 1

Course Info & Advice l See info on the World Wide Web (heavily used in Physics 111) çGo to http: //www. physics. uiuc. edu and follow “courses” link to the Physics 111 homepage l Course has several components: çLecture: (me talking, demos and Active learning) çDiscussion sections (group problem solving) çHomework sets, Web based çLabs: (group exploration of physical phenomena) çIf you miss a lab or discussion you should always try to make it up as soon as possible in another section!! l The first few weeks of the course should be review, hence the pace is fast. It is important for you to keep up! Physics 111: Lecture 1, Pg 2

Lecture Organization l Three main components: çLecturer discusses class material » Follows lecture notes very closely çLecturer does as many demos as possible » If you see it, you gotta believe it! » Look for the symbol çStudents work in groups on conceptual “Active Learning” problems » Usually three per lecture Physics 111: Lecture 1, Pg 3

Scope of Physics 111 l Classical Mechanics: çMechanics: How and why things work çClassical: » Not too fast (v << c) » Not too small (d >> atom) l Most everyday situations can be described in these terms. çPath of baseball çOrbit of planets çetc. . . Physics 111: Lecture 1, Pg 4

Units l l How we measure things! All things in classical mechanics can be expressed in terms of the fundamental units: çLength çMass çTime l L M T For example: çSpeed has units of L / T (i. e. miles per hour). çForce has units of ML / T 2 etc. . . (as you will learn). Physics 111: Lecture 1, Pg 5

Length: Distance Radius of visible universe To Andromeda Galaxy To nearest star Earth to Sun Radius of Earth Sears Tower Football field Tall person Thickness of paper Wavelength of blue light Diameter of hydrogen atom Diameter of proton Length (m) 1 x 1026 2 x 1022 4 x 1016 1. 5 x 1011 6. 4 x 106 4. 5 x 102 1. 0 x 102 2 x 100 1 x 10 -4 4 x 10 -7 1 x 10 -10 1 x 10 -15 Physics 111: Lecture 1, Pg 6

Time: Interval Age of universe Age of Grand Canyon 32 years One year One hour Light travel from Earth to Moon One cycle of guitar A string One cycle of FM radio wave Lifetime of neutral pi meson Lifetime of top quark Time (s) 5 x 1017 3 x 1014 1 x 109 3. 2 x 107 3. 6 x 103 1. 3 x 100 2 x 10 -3 6 x 10 -8 1 x 10 -16 4 x 10 -25 Physics 111: Lecture 1, Pg 7

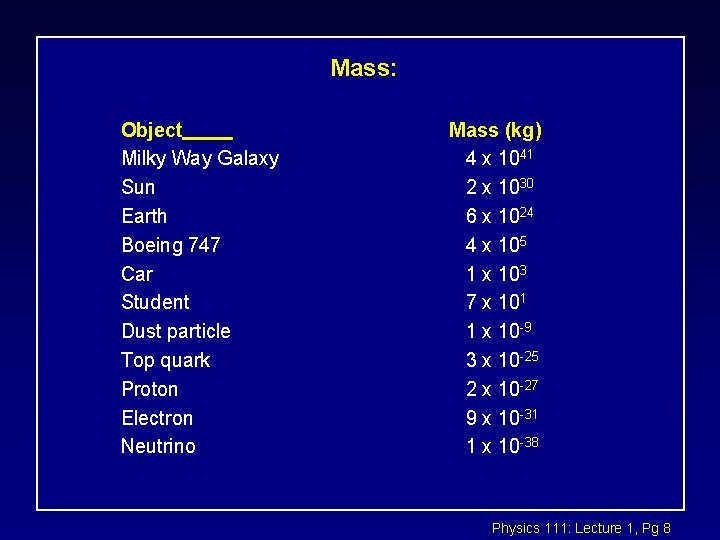
Mass: Object Milky Way Galaxy Sun Earth Boeing 747 Car Student Dust particle Top quark Proton Electron Neutrino Mass (kg) 4 x 1041 2 x 1030 6 x 1024 4 x 105 1 x 103 7 x 101 1 x 10 -9 3 x 10 -25 2 x 10 -27 9 x 10 -31 1 x 10 -38 Physics 111: Lecture 1, Pg 8

Units. . . l SI (Système International) Units: çmks: L = meters (m), M = kilograms (kg), T = seconds (s) çcgs: L = centimeters (cm), M = grams (gm), T = seconds (s) l British Units: çInches, feet, miles, pounds, slugs. . . l We will use mostly SI units, but you may run across some problems using British units. You should know how to convert back & forth. Physics 111: Lecture 1, Pg 9

Converting between different systems of units l Useful Conversion factors: ç 1 inch = 2. 54 cm ç 1 m = 3. 28 ft ç 1 mile = 5280 ft ç 1 mile = 1. 61 km l Example: convert miles per hour to meters per second: Physics 111: Lecture 1, Pg 10

Dimensional Analysis l This is a very important tool to check your work çIt’s also very easy! l Example: Doing a problem you get the answer distance d = vt 2 (velocity x time 2) Units on left side = L Units on right side = L / T x T 2 = L x T l Left units and right units don’t match, so answer must be wrong!! Physics 111: Lecture 1, Pg 11

Lecture 1, Act 1 Dimensional Analysis l (a) The period P of a swinging pendulum depends only on the length of the pendulum d and the acceleration of gravity g. çWhich of the following formulas for P could be correct ? P = 2 (dg)2 (b) (c) Given: d has units of length (L) and g has units of (L / T 2). Physics 111: Lecture 1, Pg 12

Lecture 1, Act 1 Solution l l Realize that the left hand side P has units of time (T ) Try the first equation (a) Not Right !! (b) (c) Physics 111: Lecture 1, Pg 13

Lecture 1, Act 1 Solution l Try the second equation (b) (a) Not Right !! (b) (c) Physics 111: Lecture 1, Pg 14

Lecture 1, Act 1 Solution l Try the third equation (c) This has the correct units!! This must be the answer!! (a) (b) (c) Physics 111: Lecture 1, Pg 15

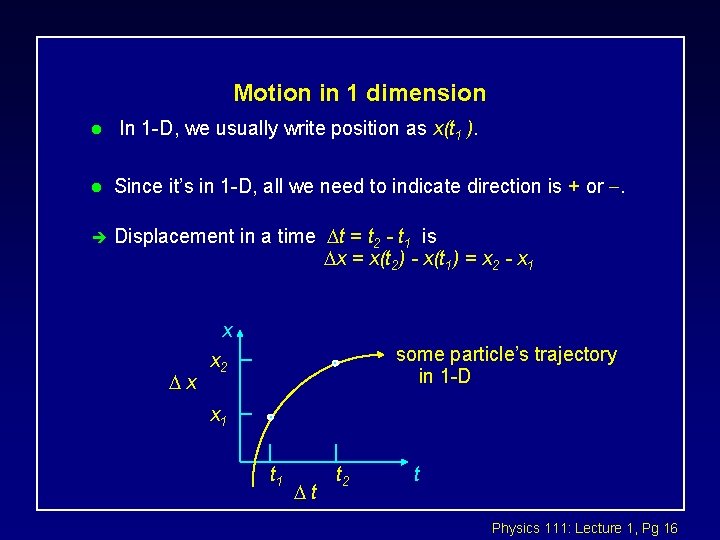
Motion in 1 dimension l In 1 -D, we usually write position as x(t 1 ). l Since it’s in 1 -D, all we need to indicate direction is + or . è Displacement in a time t = t 2 - t 1 is x = x(t 2) - x(t 1) = x 2 - x 1 x x some particle’s trajectory in 1 -D x 2 x 1 t 1 t t 2 t Physics 111: Lecture 1, Pg 16

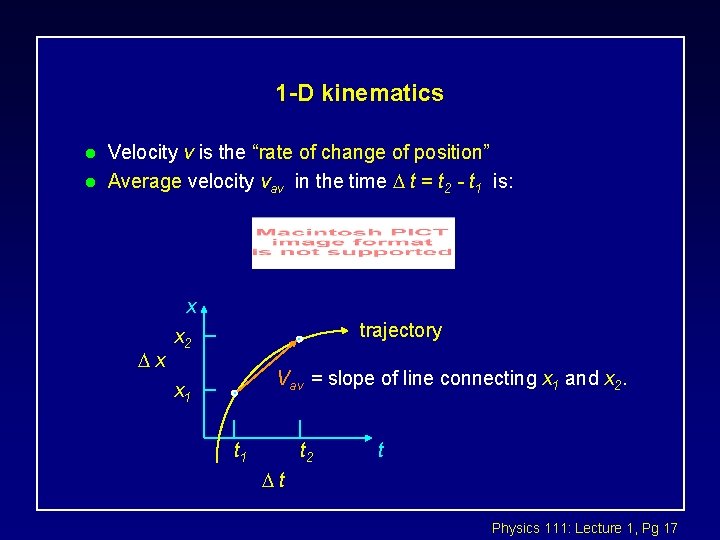
1 -D kinematics l l Velocity v is the “rate of change of position” Average velocity vav in the time t = t 2 - t 1 is: x x trajectory x 2 Vav = slope of line connecting x 1 and x 2. x 1 t 2 t t Physics 111: Lecture 1, Pg 17

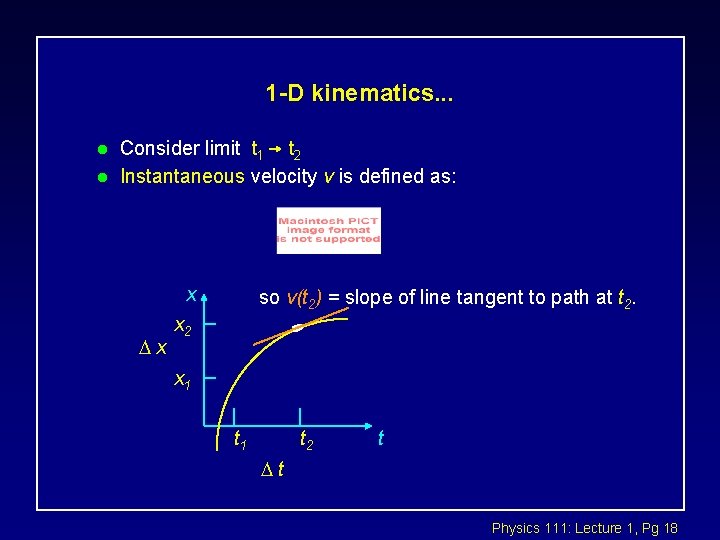
1 -D kinematics. . . l l Consider limit t 1 t 2 Instantaneous velocity v is defined as: x x so v(t 2) = slope of line tangent to path at t 2. x 2 x 1 t 2 t t Physics 111: Lecture 1, Pg 18

1 -D kinematics. . . l Acceleration a is the “rate of change of velocity” Average acceleration aav in the time t = t 2 - t 1 is: l And instantaneous acceleration a is defined as: l using Physics 111: Lecture 1, Pg 19

Recap l If the position x is known as a function of time, then we can find both velocity v and acceleration a as a function of time! x v a t t t Physics 111: Lecture 1, Pg 20

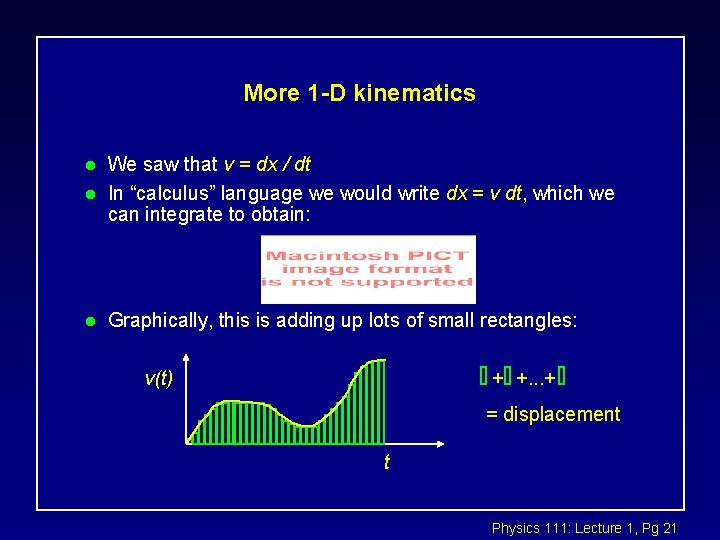
More 1 -D kinematics l We saw that v = dx / dt In “calculus” language we would write dx = v dt, which we can integrate to obtain: l Graphically, this is adding up lots of small rectangles: l v(t) + +. . . + = displacement t Physics 111: Lecture 1, Pg 21

1 -D Motion with constant acceleration l High-school calculus: l Also recall that l Since a is constant, we can integrate this using the above rule to find: l Similarly, since we can integrate again to get: Physics 111: Lecture 1, Pg 22

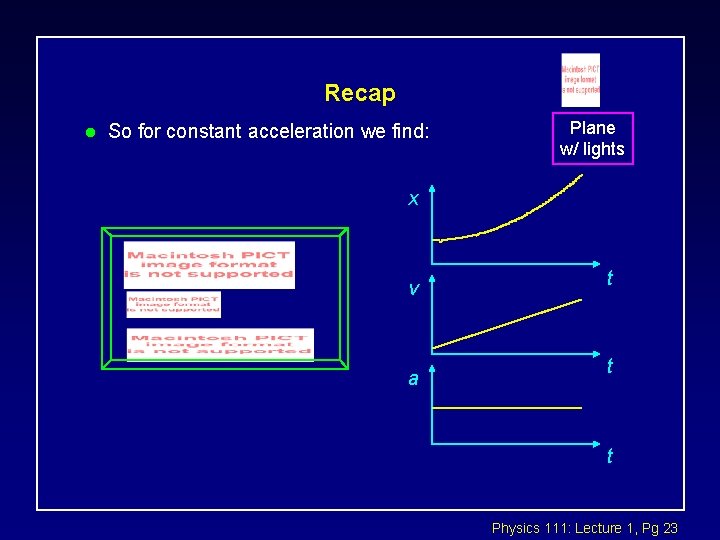
Recap l So for constant acceleration we find: Plane w/ lights x v a t t t Physics 111: Lecture 1, Pg 23

Lecture 1, Act 2 Motion in One Dimension l When throwing a ball straight up, which of the following is true about its velocity v and its acceleration a at the highest point in its path? (a) Both v = 0 and a = 0. (b) v 0, but a = 0. y (c) v = 0, but a 0. Physics 111: Lecture 1, Pg 24

Lecture 1, Act 2 Solution l Going up the ball has positive velocity, while coming down it has negative velocity. At the top the velocity is momentarily zero. x l Since the velocity is continually changing there must v be some acceleration. çIn fact the acceleration is caused by gravity (g = 9. 81 m/s 2). ç(more on gravity in a few lectures) a l The answer is (c) v = 0, but a 0. t t t Physics 111: Lecture 1, Pg 25

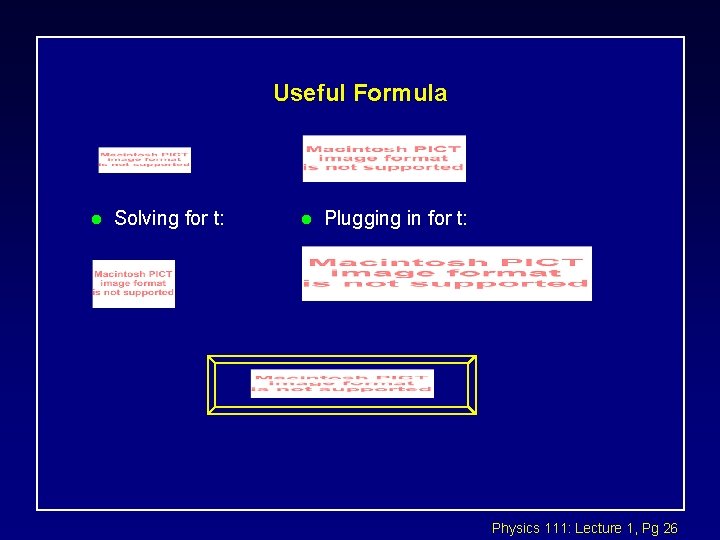
Useful Formula l Solving for t: l Plugging in for t: Physics 111: Lecture 1, Pg 26

Alternate (Calculus-based) Derivation (chain rule) (a = constant) Physics 111: Lecture 1, Pg 27

Recap: l For constant acceleration: l From which we know: Washers Physics 111: Lecture 1, Pg 28

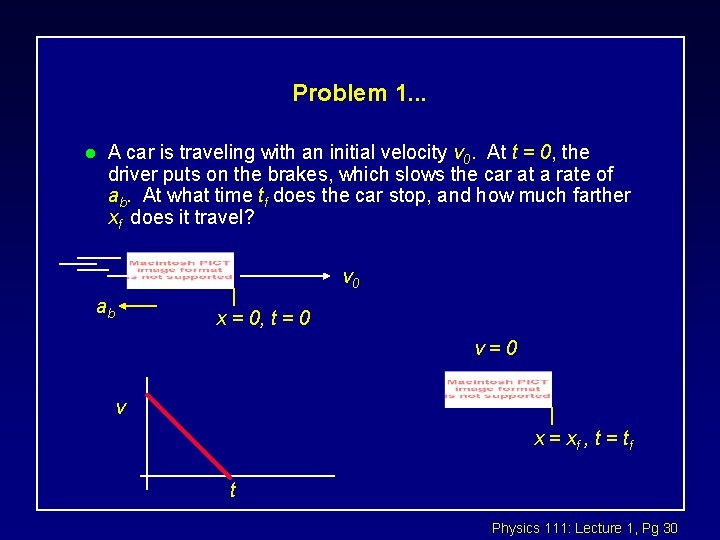
Problem 1 l A car is traveling with an initial velocity v 0. At t = 0, the driver puts on the brakes, which slows the car at a rate of ab vo ab x = 0, t = 0 Physics 111: Lecture 1, Pg 29

Problem 1. . . l A car is traveling with an initial velocity v 0. At t = 0, the driver puts on the brakes, which slows the car at a rate of ab. At what time tf does the car stop, and how much farther xf does it travel? v 0 ab x = 0, t = 0 v=0 v x = xf , t = t f t Physics 111: Lecture 1, Pg 30

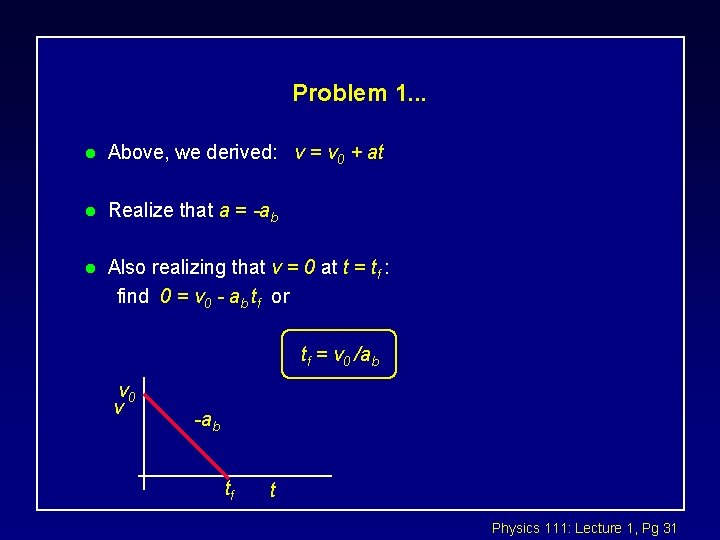
Problem 1. . . l Above, we derived: v = v 0 + at l Realize that a = -ab l Also realizing that v = 0 at t = tf : find 0 = v 0 - ab tf or tf = v 0 /ab v 0 v -ab tf t Physics 111: Lecture 1, Pg 31

Problem 1. . . l To find stopping distance we use: l In this case v = vf = 0, x 0 = 0 and x = xf v 0 v -ab tf t Physics 111: Lecture 1, Pg 32

Problem 1. . . l l l So we found that Suppose that vo = 65 mi/hr = 29 m/s Suppose also that ab = g = 9. 81 m/s 2 ç Find that tf = 3 s and xf = 43 m 29 m/s v - 9. 81 m/s 2 43 m 3 s t Physics 111: Lecture 1, Pg 33

Tips: l Read ! çBefore you start work on a problem, read the problem statement thoroughly. Make sure you understand what information is given, what is asked for, and the meaning of all the terms used in stating the problem. l Watch your units ! çAlways check the units of your answer, and carry the units along with your numbers during the calculation. l Understand the limits ! çMany equations we use are special cases of more general laws. Understanding how they are derived will help you recognize their limitations (for example, constant acceleration). Physics 111: Lecture 1, Pg 34

Recap of today’s lecture l Scope of this course Measurement and Units (Chapter 1) çSystems of units (Text: 1 -1) çConverting between systems of units (Text: 1 -2) çDimensional Analysis (Text: 1 -3) 1 -D Kinematics (Chapter 2) çAverage & instantaneous velocity and acceleration (Text: 2 -1, 2 -2) çMotion with constant acceleration (Text: 2 -3) Example car problem (Ex. 2 -7) l Look at Text problems Chapter 2: # 49, 54, 71, 122 l l l Physics 111: Lecture 1, Pg 35