ECO 365 Intermediate Microeconomics Lecture Notes Monopoly Market

ECO 365 – Intermediate Microeconomics Lecture Notes

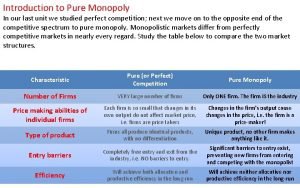
Monopoly � Market environment where there is only one firm in the market � Firm faces ALL of demand � So monopoly profit = p(y)y – c(y) � Where p(y) = inverse market demand let p(y)y = r(y) revenue function � � Monopolistic problem: Choose y to Max r(y) – c(y) First order conditions are given by: MR = MC

�The same condition we got with perfect competition �But now MR does not equal P (i. e. firms not price takers) �Two effects of changing y (say increase y) on revenues � 1 -sell more so revenue increases � 2 -price decreases so revenue decreases � ∆ r (y) = p ∆y + y ∆p � ∆ r(y)/ ∆ y = MR = p + y ∆p/ ∆y or: � For price takers ∆p=0 => ∆r = p ∆y � But now P decreases as y increases so the second term matters.

�Now both 1 and 2 measure Marginal Revenue (MR) �MR= ∆r/ ∆y = p + y ∆p/ ∆y �= p(1 + (y/p)(∆p/ ∆y) �= p(y) (1 + 1/ε) �Since ε = price elasticity of demand = (p/y)(∆y/∆p) �=> can re-write optimal condition, MR = MC as: � p(y) (1 + 1/ ε(y)) = mc (y) �Or p(y) (1 - 1/| ε(y)|) = mc (y) � Since ε < 0 � Also recall that | ε | > 0 elastic � | ε | < 1 inelastic � So that if demand elastic regions | ε | > 1 � MR > 0 but if demand inelastic MR < 0

�The above implies that the Monopolist only operates in elastic portion of Demand since � MR < 0 when demand inelastic and profit max. requires MR = MC but MC < 0 is unlikely (impossible). �Now with linear demand… �P(y) = a –b y �So R (y) = ay –by 2 �=> MR= a – 2 by �Notice 3 things: � 1. MR = D at y=0 � 2. slope of MR = 2 times the slope of demand (i. e. , twice as steep). � 3. MR = 0 where | ε | = 1 (this is always true not just for linear Demand)

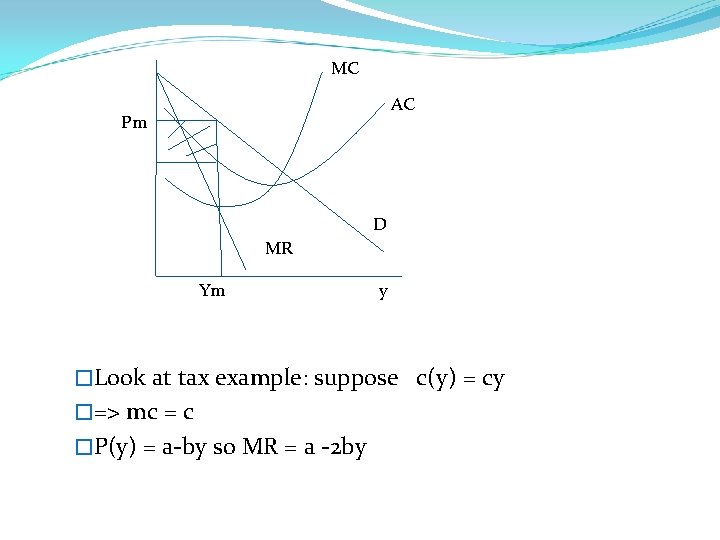
MC AC Pm D MR Ym y �Look at tax example: suppose c(y) = cy �=> mc = c �P(y) = a-by so MR = a -2 by

�Now suppose a tax on the monopolist = t (quantity tax) so pc = ps + t �So mc w/ tax is c + t or c(y) = (c+ t)y �=> before profit max where c = a -2 by �Or y* = a-c/2 b �Now MC = c + t = a – 2 by = MR �So y* = (a-c-t)/2 b �=> Δy/ Δ t = -1/(2 b) (why? ) �What is the impact of the tax on price, p? Recall slope of demand function = Δp/ Δy = -b, so � The tax is imposed => y changes by -1/(2 b) then � The price changes by – b, the overall impact is both of these together, � Or – b times -1/(2 b) = -1/2 � �Interpretation: if t increases by $1 => price increases by $. 50

pt P* C+t MC = C MR Yt D y* �But note that p may actually increase more than by the amount of tax. See book for example

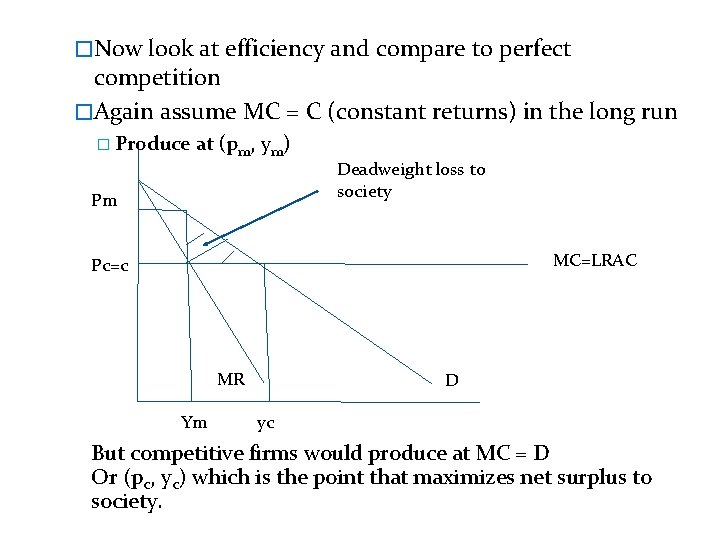
�Now look at efficiency and compare to perfect competition �Again assume MC = C (constant returns) in the long run � Produce at (pm, ym) Pm Deadweight loss to society MC=LRAC Pc=c MR Ym D yc But competitive firms would produce at MC = D Or (pc, yc) which is the point that maximizes net surplus to society.

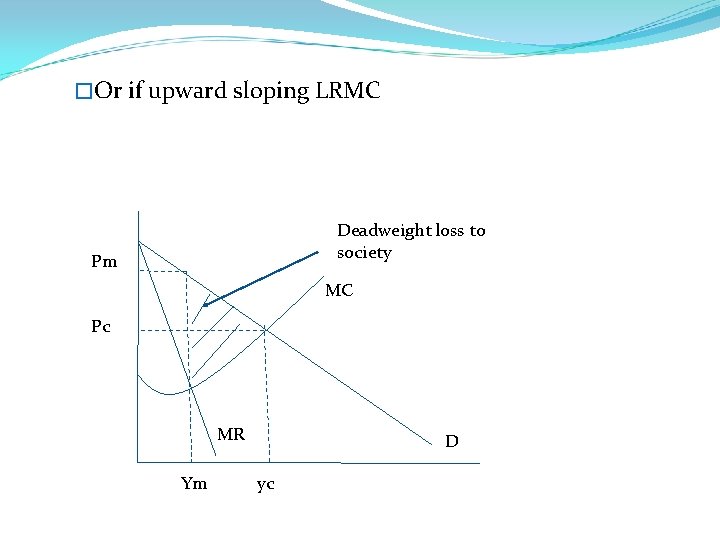
�Or if upward sloping LRMC Deadweight loss to society Pm MC Pc MR Ym D yc

�=> appears that monopolist is inefficient (i. e. does not max society’s net surplus) �Public policy: may be to get rid of monopolies �(1) contestable markets i. e. free entry => if profit > 0 more firms enter so profit = o even with one firm. �(2) economies of scale and scope � Consider natural monopoly (economies of scale) Pm Pt LRMC LRAC MR Ym D

�Only one firm can cheaply produce given demand but � (1) if p=mc=Pso(socially optimum price) � Firms makes a loss and leaves � (2) if p=pm => deadweight loss � (3) if p=AC=pf (fair price) still a loss in profit but firm can operate � But if break up of monopoly: � Pc > Pm > Pf >Pso => competition is not more efficient due to economies of scale. � Same may to be true due to economies of scope.

�Price Discrimination � 3 different types � A. Perfect price discrimination—price the monopolists sells is just equal to your willingness to pay => � With no price discrimination produce at (pm, ym) but this assumes no ability to discriminate Pm Pe MC D MR Ym � Now Ye perfectly discriminate => D=MR and produce at Yc which is efficient (assuming $1 to producer is the same as $1 to consumer since CS=0)

� 2 nd degree Price Discrimination � Pi= f(yi) i. e. how much you pay depends on your consumption � Examples: utilities, bulk discounts for large purchases � 3 rd degree price discrimination-different groups get different prices but individuals within a group get the same price �Most common type: Examples � 1. movie theatre discounts (kids v. adults) � 2. local ski discounts (locals v. non-locals) � More formally suppose 2 groups with different demand � => max P 1 (Y 1) Y 1 + P 2 (Y 2) Y 2 – C(Y 1 + Y 2) by: � MR 1 – MC(Y 1 + Y 2) = 0 � MR 2 – MC(Y 1 + Y 2) = 0

�Combine to get MR 1 = MC(Y 1 + Y 2) = MR 2 or �P 1 [1 - 1/| ε 1 |] = MC (Y 1 +Y 2) = P 2 [1 -1/| ε 2|] �If P 1 > P 2 => [1 -1/| ε 1|] < 1 – 1/| ε 2| or � 1/| ε 1| > 1/| ε 2| or | ε 2| > | ε 1| �i. e. for P 1 > P 2 demand for group 1 must be more inelastic �Graphically, assume C= MC Group 1 Group 2 P 1 D 1 C MR 1 Y 1 P 2 C MR 2 Y 2 D 2

�Innovation—monopolies have more incentive to innovate (at least this is the argument) �Define innovation �Just a decrease in MC to MC 2 assuming constant returns P MC 1 MC 2 Q

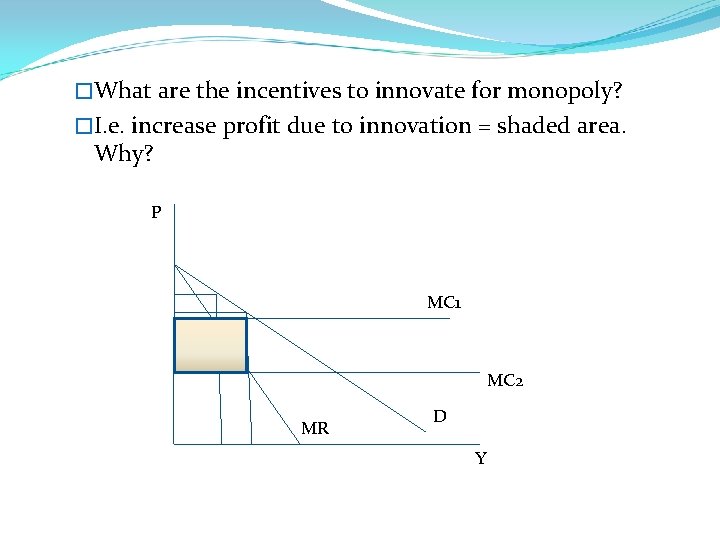
�What are the incentives to innovate for monopoly? �I. e. increase profit due to innovation = shaded area. Why? P MC 1 MC 2 MR D Y

�What are incentives to innovate for perfectly competitive industry? �None unless (1) innovative technology is secret or (2) a patent system exists �Under a patent system what is the incentive? What are increased profits to patent holder? � 1 st what does patent holders MR curve look like? As long y < y* MR = C ; i. e. he’s a price taker. P MC 1 C MC 2 C 1 D Y* Q

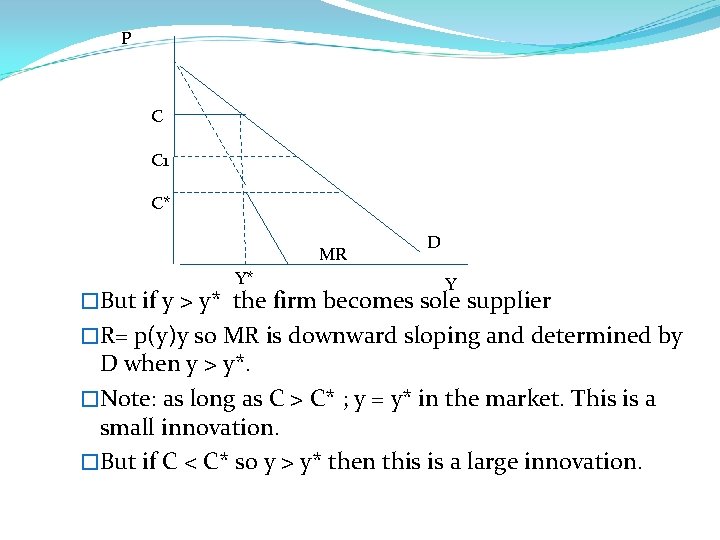
P C C 1 C* MR Y* D Y �But if y > y* the firm becomes sole supplier �R= p(y)y so MR is downward sloping and determined by D when y > y*. �Note: as long as C > C* ; y = y* in the market. This is a small innovation. �But if C < C* so y > y* then this is a large innovation.

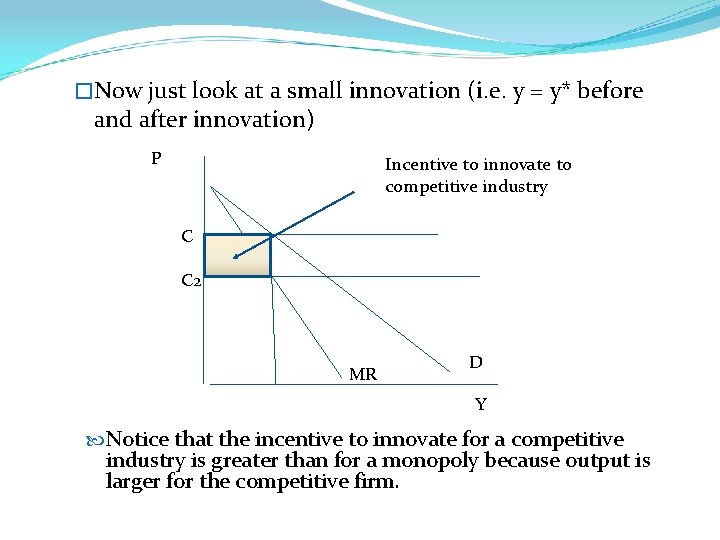
�Now just look at a small innovation (i. e. y = y* before and after innovation) P Incentive to innovate to competitive industry C C 2 MR D Y Notice that the incentive to innovate for a competitive industry is greater than for a monopoly because output is larger for the competitive firm.

�Q: What if economies of scale in innovation (i. e. small firms in competitive industry don’t have resources to innovate) �A: Firms specialize in innovating, gain patents and license to small competitive firms � Example: agriculture where innovating is done by � Universities � Seed companies � Etc.

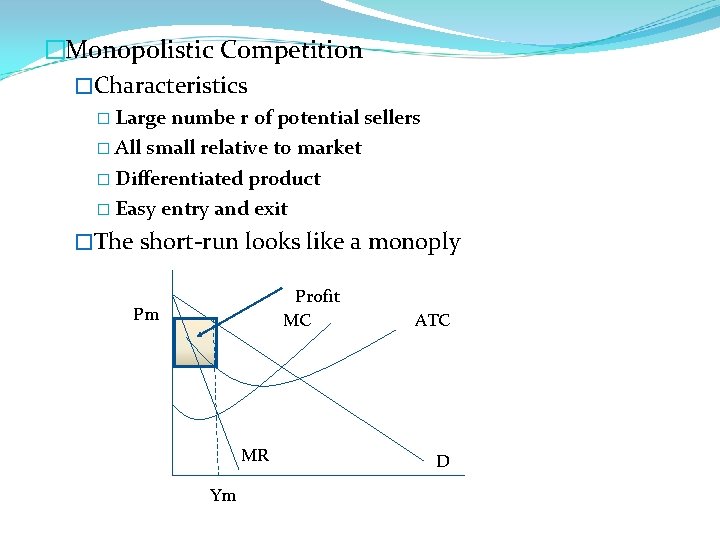
�Monopolistic Competition �Characteristics � Large numbe r of potential sellers � All small relative to market � Differentiated product � Easy entry and exit �The short-run looks like a monoply Profit MC Pm MR Ym ATC D

�Profit can also be negative or zero in the short-run. If negative => firms exit if p< avc. �Long-run equilibrium is just like for competition: �If profit > 0 => entry which drives profit down. �If profit < 0 => exit which drives profit up. �Therefore, long-run equilibrium is where profit equals zero, where no exit or entry. MC ATC Po Pc MR Qo Qc D

�Notice that at Equilibrium but P > MC �Resource Allocation & Efficiency � Since MSC does not equal MSB or MSB > MSC => inefficient p. c. firm would produce the efficient amount. � Might be efficient if benefit from different products > Cost of producing different products � => in long run (1) each firm is on its demand curve � (2) each firm chooses y to max profit � (3) entry forces profit = 0 � (4) P > MC => inefficient