ECO 365 Intermediate Microeconomics Lecture Notes Oligopoly P

ECO 365– Intermediate Microeconomics Lecture Notes

Oligopoly P. C. (1) M. C. (3) Oligopoly (4) Monopoly (2) Oligopoly = a few competitors > 1 All have impact on others reactions and decisions For 1/3 => lots of competitors but all so small (don’t care) For 2 => only 1 firm, no competitors Oligopoly unique in that each firm must react to competitors How?

Multiple ways => oligopoly is difficult to model because there is not just 1 model but multiple models. Duopoly: 2 firms (simpler) Price leader/follower Q leader/follower Collusion No followers but simultaneous decisions => how? Sequential games, cooperate games, simultaneous games Plus many more

Do 2 types of models first Cournot: each firm chooses yi given belief about yi => EQ where beliefs true. Stackelberg- Q leader, Q follower model => dominant firm These are actually similar models Do the basics of both models first

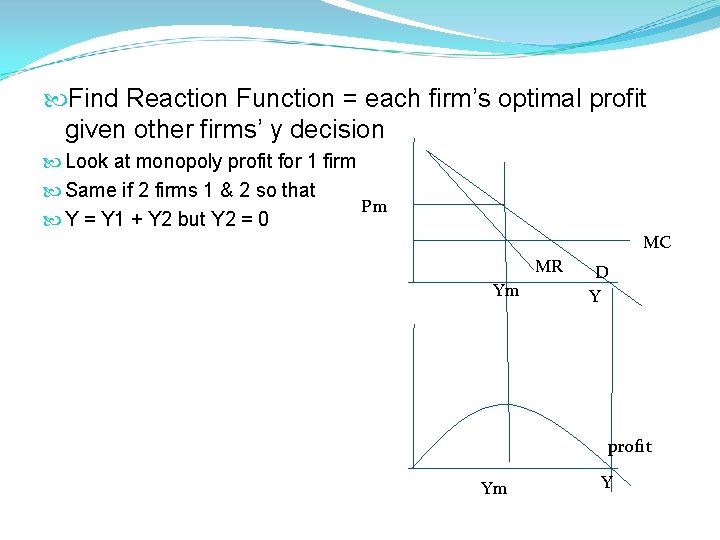
Find Reaction Function = each firm’s optimal profit given other firms’ y decision Look at monopoly profit for 1 firm Same if 2 firms 1 & 2 so that Pm Y = Y 1 + Y 2 but Y 2 = 0 MC MR Ym D Y profit Ym Y

But suppose Y 2 > 0 => D for 1 decreases => 1 is the residual claimant P For D 1 Y 2=Z-E MRm Ym is optimal MC Assuming Y 2=0 MR D 1 Dm Y 1* is optimal Y 1* Ym E Z Y assuming Y 2 = Z-E π π|Y 2=Z-E π|Y 2=0 Y

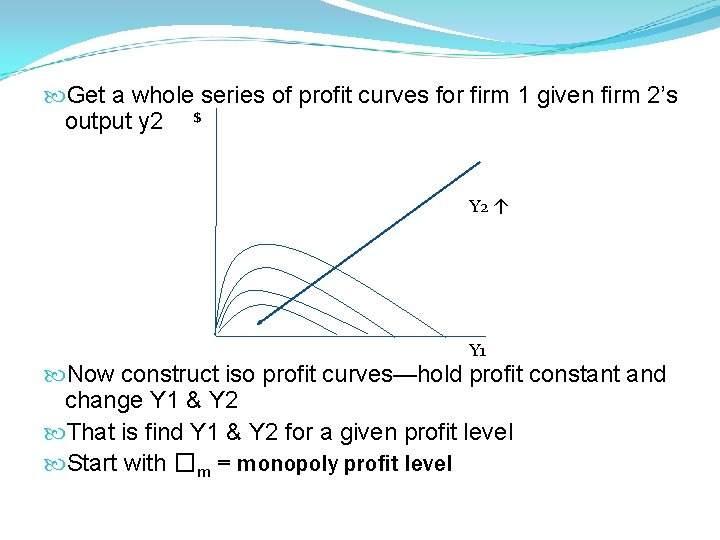
Get a whole series of profit curves for firm 1 given firm 2’s output y 2 $ Y 2 ↑ Y 1 Now construct iso profit curves—hold profit constant and change Y 1 & Y 2 That is find Y 1 & Y 2 for a given profit level Start with �m = monopoly profit level

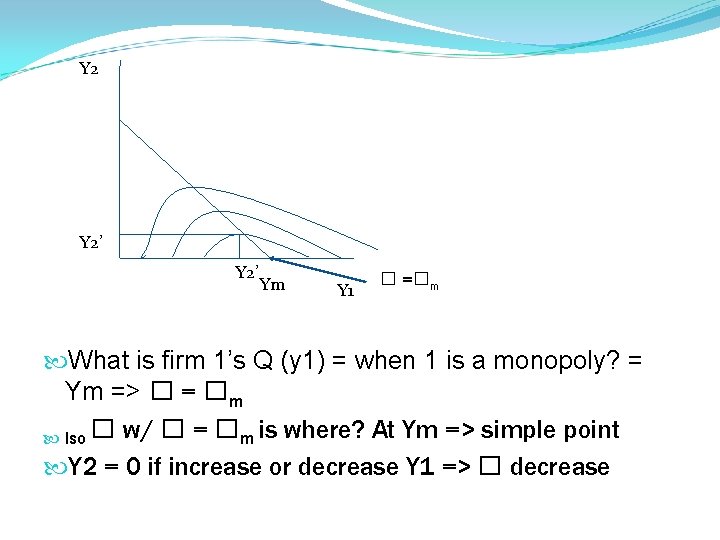
Y 2 Y 2’ Ym Y 1 � =�m What is firm 1’s Q (y 1) = when 1 is a monopoly? = Ym => � = �m Iso � w/ � = �m is where? At Ym => simple point Y 2 = 0 if increase or decrease Y 1 => � decrease

Now suppose Y 2 increases => profit decreases what happens to optimal Y 1 w/ an increase in Y 2? Proved before that it decreases but so does � 1. If Y 2 = Y 2’ => firm 1 chooses Y 1’ Firm 1 can choose a different level of Y 1 than Y 1’ but either increase or decrease Y 1 will decrease profit given Y 2=Y 2’ A firm’s reaction function (ridge line) shows that firm’s max profit given other firm’s y

Do the same for Firm 2: Looks like… Y 2 � 2 increase � 1 increase Ym Firm 1’s reaction Fn Y 1 Firm 2’s reaction Fn

Book shows that for P = a-b y Y 2 = (a- b Y 1) / 2 b Y 1= (a – b Y 2)/2 b Assuming MC = 0 if MC =C (constant Y 2= (a- b Y 1 – C) / 2 b Y 1= (a – b Y 2 – C) / 2 b Gets more complicated if MC = F (Y 1) Common to assume MC = Constant

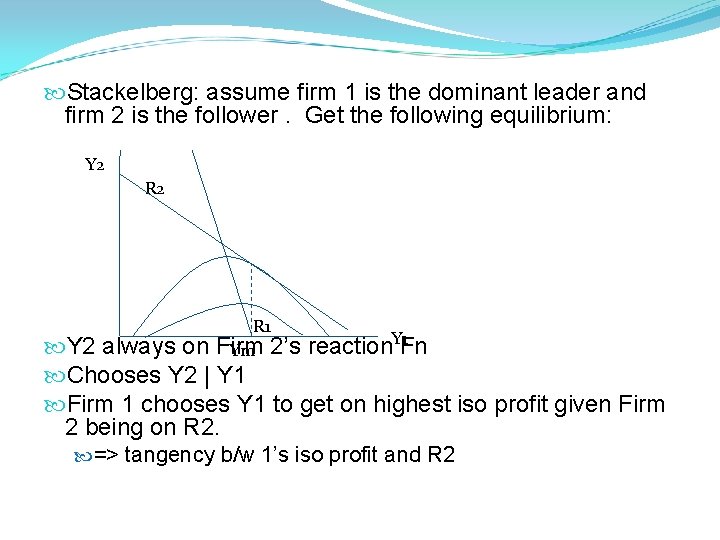
Stackelberg: assume firm 1 is the dominant leader and firm 2 is the follower. Get the following equilibrium: Y 2 R 1 Firm Ym 2’s Y 2 always on reaction. Y 1 Fn Chooses Y 2 | Y 1 Firm 1 chooses Y 1 to get on highest iso profit given Firm 2 being on R 2. => tangency b/w 1’s iso profit and R 2

Cournot each firm on its reaction Fn and eq. only if expectations about other firm next Point A not Cournot Eq. Y 2 D C A B R 1 Ym R 2 Y 1 At A 1 would move to B; at B 2 would move to C and so on until eventually get to D where R 1 and R 2 cross and E 2 (Y 1) = Y 1 E 1 (Y 2) = Y 2

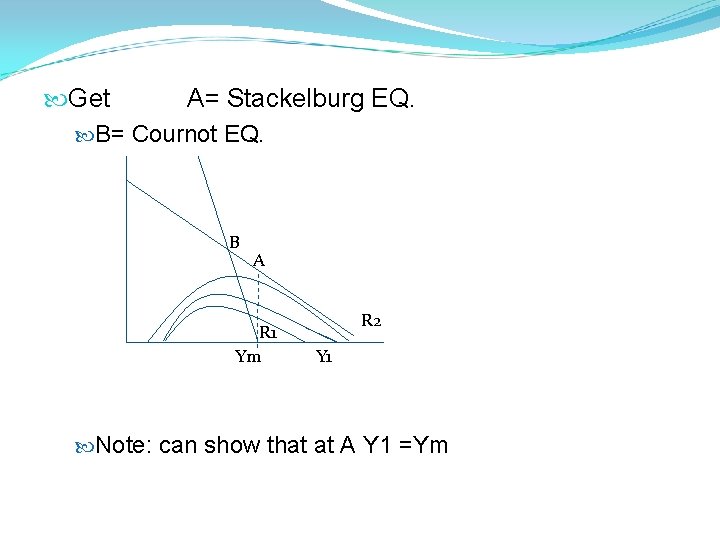
Get A= Stackelburg EQ. B= Cournot EQ. B A R 1 Ym R 2 Y 1 Note: can show that at A Y 1 =Ym

Define Nash EQ= Both parties Choosing optimally to max profit given info they have Cournot = Nash Eq Stackelberg = not Nash Eq 1’s higher than 2 =>return to not being a reaction function

Now suppose both oligopoly players realize this simultaneously and play Stackelburg Y 1 = Y 2 = Ym => Y = Ym + Ym = the competitive output � a=� b = 0 => by playing “smart” both firms get less profit. Stackelburg bluff if 1 or 2 can convince the other player that he will stay at Qm no matter what => the other players rational move is to go to his reaction function since profit increases if he does so. Both want to be this player. Y 2 Ym Esc Ess Ecc Ecs Ym Y 1

Collusion implies joint �max (i. e. on Ym-Ym) but here there is a problem with cheating If at E on collusive agreement A or B can get to a lower �hill (more � ) by increasing q a little => incentives to cheat.

If they both cheat then they are both worse off. Bertrand Model: the only difference between Cournot and Bertrand model is that price (not qty) is used as the choice variable. Let Q = D(P) be the demand function. The problem is to max � 1 = D(P 1) P 1 – C (P 1) P 2 = P 2 Everything is a function of price P MC Qm Qc Q

Look at Eq. If P > MC => 1 firm can increase Q (increase � ) by decreasing P slightly the other will follow and P decreases to MC If P=MC and 1 firm increases P, Q decreases to o so no increase in � => P = MC is an equilibrium Now what if MC is upward sloping? Then what is the equilibrium? EQ does not exist because it is always optimum to change price. If P = MC incentive is to increase price i. e. if 1 firm increases P => at old price consumers want to buy more of other firms price also => both increase price (z) if p= monopoly price (and each firm has ½ Qm) => >MC and by decreasing price can get more �=> both decrease price until P=MC

Game Theory Applied to Oligopoly Game theory: method of analyzing outcomes of choices made by people who are interdependent. Define: Players: those making choices Strategies: the possible choices to achieve ____ Payoffs: returns to different choices Payoff matrix: shows how different choices affect payoffs For example: A owns A house with his value of $60 k. B values House at $80 K and has $70 K => Possibility of exchange (1) Cooperative solution: reach an agreement over price and exchange occurs (2) non-cooperative solution => no exchange

Q: What does each party get in both cases? For 2: A gets house = $60 k; B gets $70, 000 => total of $130 K For 1: A gets $70, 000 and B gets house - $80 K => total of $150 k => Cooperative surplus = $20, 000 What would the payoff matrix look like? 1 st: what are the decisions? Suppose bargain hard v. soft If you bargain hard and other soft=> assume you get A 4 surplus If both bargain soft => split surplus If both bargain hard=> no exchange and no surplus H H S 60 K 70 K 60 K 90 K 80 K S 70 K 80 K

Note: Reach cooperative solution as long as not H 1, H. Q: What will the _____ be? Look at A’s choice If B choose S => A better off with H If B choose H => A indiff. for H & S => A choose H => B choose H => H 1 H = Eq. Essentially this is a dominant strategy game (not quite because of the ind. )

Look at the 2 games from the book 1 st: Dominant Strategy Game Low Q High Q 10 High Q 30 20 9 17 20 25 18 Both firms better off with choosing High Q

2 nd– What should A choose? Low Q High Q 22 High Q 30 20 9 17 20 25 18 Clearly depends on what B chooses A: Low Q => Low Q; High Q => High Q But B has a dominant strategy = High Q => A also chooses High Q Nash Eq: each player chooses best one given stratgey chosen by other. Now look at the prisoner’s dilemma: Common/classic game and widely applicable to many other situations including firm decisions.

2 people arrested for whatever (book uses drug dealing) Suppose choices presented = confess, don’t confess with payoff matrix = Confess Don’t C 10 yr D 15 yr 15 yr 2 yr 2 points: both have a dominant strategy= confess => both confess Cooperative surplus available, that is D 1 D = cooperation and better off there then at the actual EQ. Why don’t they? Not just because believe other will confess, more than that because better off to confess regardless of what the other does.

How to deal with Prisoner’s Dilemma? Mob does it by charging payoff matrix to increase penatly if confess C C D death D 15 yr death 15 yr 2 yr Now don’t confess = Nash Eq and dominant strategy => D 1 D

Mixed vs. Pure Strategy Pure: make choice and stick with it Mixed: make a choice some % of the time. Where % of sum to 1 for all possible choices Example: Left Right Top bottom 0, 0 0, -1 1, 0 -1, 3 First, with mixed strategies always Nash Eq => each party chooses optimal prob. given the other parties prob. Second, not always Nas Eq w/ Pure Strategies

____ above 1 st with Pure Strategy If B = L => A = B If B = R => A = T If A = T => B = L If A = B => B = R Notice how no eq. exists With mixed strategy, can show Nash Eq= A P(T) = ¾ P(B) = ¼ B P(L) = ½ P(R) = ½ How?

Look at expected values with prob. Define EU Let p = prob. A plays top 1 -p = prob A plays bottom q= prob B plays left 1 -q= prob B plays right => each party’s EU depends on other party’s choice of their prob. For example: If A plays Top => EUA 1 = 0 q + 0(1 -q) If A plays bottom => EQA 2 = 1 q + -1 (1 -q) If B plays left => EUB 1 = 0 P + 0(1 -P) If B plays right =>EUB 2 = -1 P + 3(1 -P) What is the EQ con

Q occurs when no change in behavior If for A EUA 1 = EUA 2 => no reason for A to change behavior if > or 0 = q – (1 -q) if L < decrease in P 0 = q – 1 + q 1 = 2 q or q = ½ (1 -q) = ½ Same for B EUB 1 = EUB 2 => or 0 = -P + (1 -P) 0= -P + 3 – 3 P 4 P =3 P= ¾(1 -P) =1/4 This is the Nash EQ. in two mixed strategy games

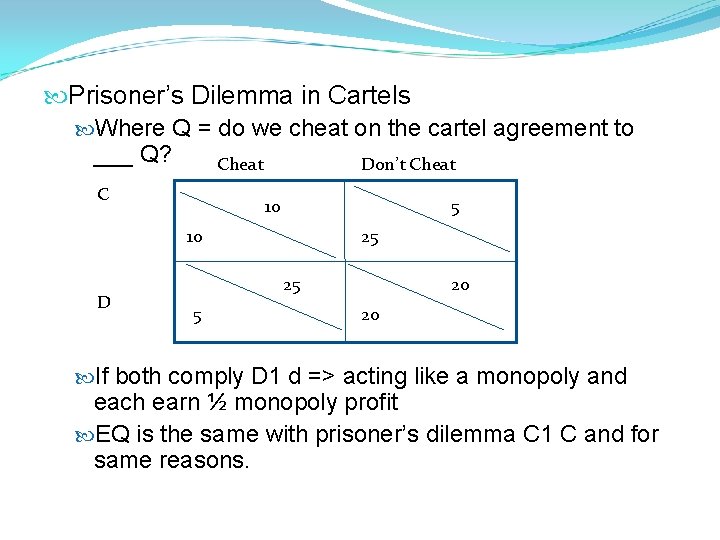
Prisoner’s Dilemma in Cartels Where Q = do we cheat on the cartel agreement to ___ Q? Cheat Don’t Cheat C 10 5 10 D 25 25 5 20 20 If both comply D 1 d => acting like a monopoly and each earn ½ monopoly profit EQ is the same with prisoner’s dilemma C 1 C and for same reasons.

Conclude Cartels only form/stable if cartel can enforce punishment of cheating Must be done so that cheating decreases profits. Perhaps they fine cheaters… C C D -10 5 -10 D 5 5 5 20 20 i. e. lose $20 if caught cheating Don’t cheat is dominant strategy for both D 1 D = Nash Eq.

Look at expected values with prob. Define EU Let p = prob. A plays top 1 -p = prob A plays bottom q= prob B plays left 1 -q= prob B plays right => each party’s EU depends on other party’s choice of their prob. For example: If A plays Top => EUA 1 = 0 q + 0(1 -q) If A plays bottom => EQA 2 = 1 q + -1 (1 -q) If B plays left => EUB 1 = 0 P + 0(1 -P) If B plays right =>EUB 2 = -1 P + 3(1 -P) What is the EQ con

Look at expected values with prob. Define EU Let p = prob. A plays top 1 -p = prob A plays bottom q= prob B plays left 1 -q= prob B plays right => each party’s EU depends on other party’s choice of their prob. For example: If A plays Top => EUA 1 = 0 q + 0(1 -q) If A plays bottom => EQA 2 = 1 q + -1 (1 -q) If B plays left => EUB 1 = 0 P + 0(1 -P) If B plays right =>EUB 2 = -1 P + 3(1 -P) What is the EQ con

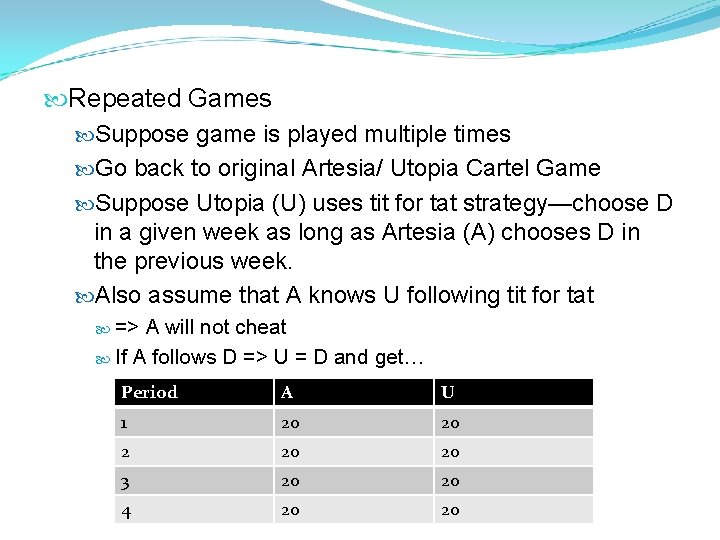
Repeated Games Suppose game is played multiple times Go back to original Artesia/ Utopia Cartel Game Suppose Utopia (U) uses tit for tat strategy—choose D in a given week as long as Artesia (A) chooses D in the previous week. Also assume that A knows U following tit for tat => A will not cheat If A follows D => U = D and get… Period A U 1 20 20 20 3 20 20 4 20 20

Which is better for A then either of the 2 strategies => not sure to get collusion but more likely because 1. firms can enforce with a tit for tat strategy 2. other firms can easily identify a tit for tat strategy

Sequential Games So far been doing simultaneous games Top bottom Left Right 1, 9 0, 0 2, 1 Notice 2 Nash EQ w/ Pure Strategy simultaneous Game 1) T, L 2) B, R Neither party can make themselves better of from these given other’s choice But, 1) is not a reasonable solution…why? A knowing matrix will never choose T => before choices knows if he chooses B => B will choose R A increases profit

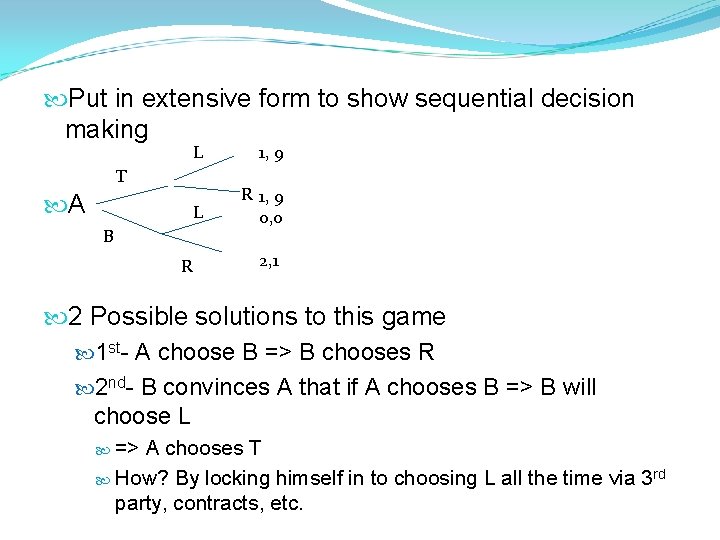
Put in extensive form to show sequential decision making L 1, 9 L R 1, 9 0, 0 T A B R 2, 1 2 Possible solutions to this game 1 st- A choose B => B chooses R 2 nd- B convinces A that if A chooses B => B will choose L => A chooses T How? By locking himself in to choosing L all the time via 3 rd party, contracts, etc.

=> Like sequence of choices, now the game becomes. . A T 1, 9 L B B 0, 0 And A chooses T Note: not necessary for the sequence to change, just look in ______ => would look like… L Other T B are gone branches 1, 9 A B L 0, 0