ECO 365 Intermediate Microeconomics Lecture Notes Firm Supply

ECO 365 – Intermediate Microeconomics Lecture Notes

Firm Supply in Competitive Markets Market Environment: ways firms interact in making pricing and output decisions. Possibilities: (1) Perfect Competition (2) Monopoly (3) Oligopoly (4) Imperfect Competition (monopolistic) In P. C. p=fixed for the producer Why? => small firms, identical products, large number of firms Examples

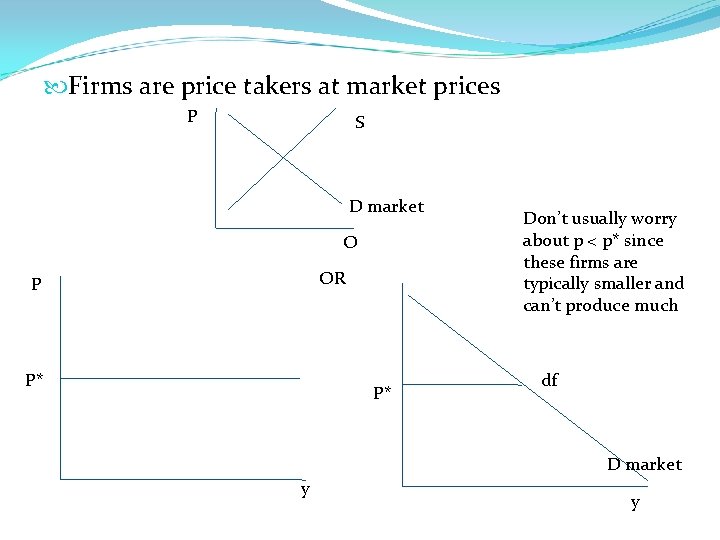
Firms are price takers at market prices P S D market O OR P P* P* Don’t usually worry about p < p* since these firms are typically smaller and can’t produce much df D market y y

The firm’s problem is to max � = py - c(y) Is this a long run or a short run problem? ∆R = p ∆ y + ∆ p y => ∆R/ ∆y = p = MR But p = MR Why? ∆C/ ∆ y = MC Choose to produce where MR=MC Why does this make sense?

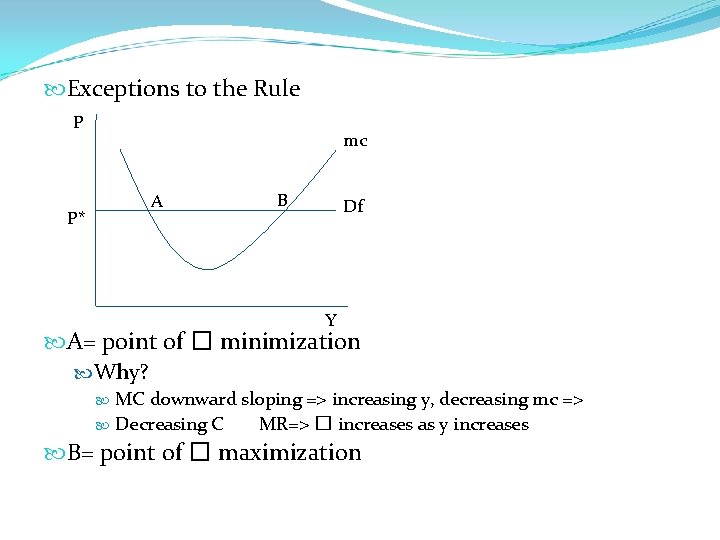
Exceptions to the Rule P P* mc A B Df Y A= point of � minimization Why? MC downward sloping => increasing y, decreasing mc => Decreasing C MR=> � increases as y increases B= point of � maximization

(1) any movement from A increases � (2) any movement from B decreases � Idea of second order conditions What does that mean? First order conditions : MR=MC Second order condtions: slope of MC > 0 Or slope of MC > Slope of MR = o => B is the correct point

2 nd Exception—Shut Down Short-Run: if shut down => lose fixed costs (F) When is this better than operating? = -F if y =0 � = py – Cv (y) – F � if y>0 So if –F > py – Cv(y) – F => shutdown or Cv(y) > py Or Cv(y)/(y) > p or p < AVC => shutdown Similarly in the Long Run: � = 0 if shutdown � = py – C(y) or p < AC

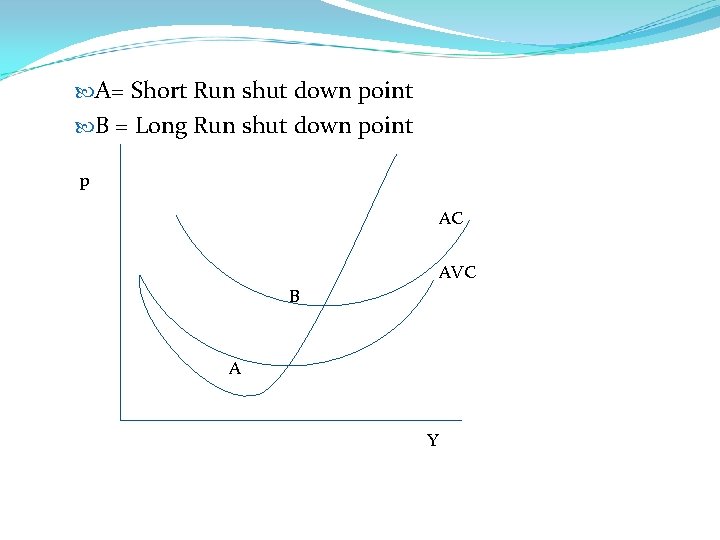
A= Short Run shut down point B = Long Run shut down point p AC AVC B A Y

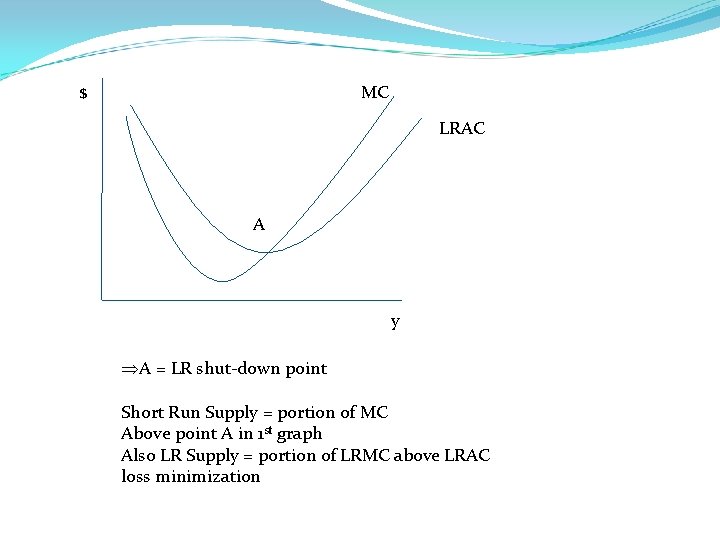
MC $ LRAC A y ÞA = LR shut-down point Short Run Supply = portion of MC Above point A in 1 st graph Also LR Supply = portion of LRMC above LRAC loss minimization

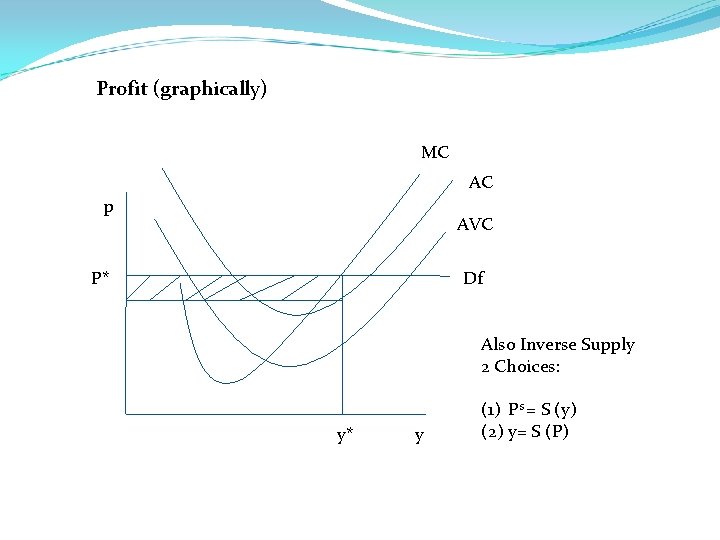
Profit (graphically) MC AC p AVC P* Df Also Inverse Supply 2 Choices: y* y (1) Ps = S (y) (2) y= S (P)

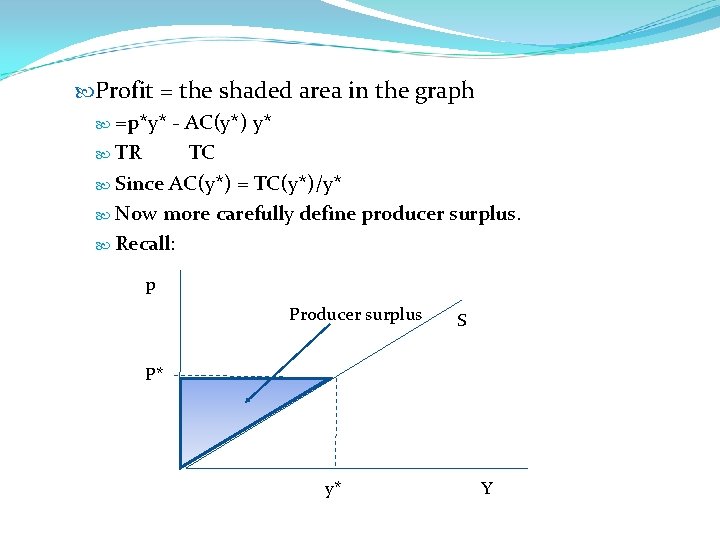
Profit = the shaded area in the graph =p*y* - AC(y*) y* TR TC Since AC(y*) = TC(y*)/y* Now more carefully define producer surplus. Recall: p Producer surplus S P* y* Y

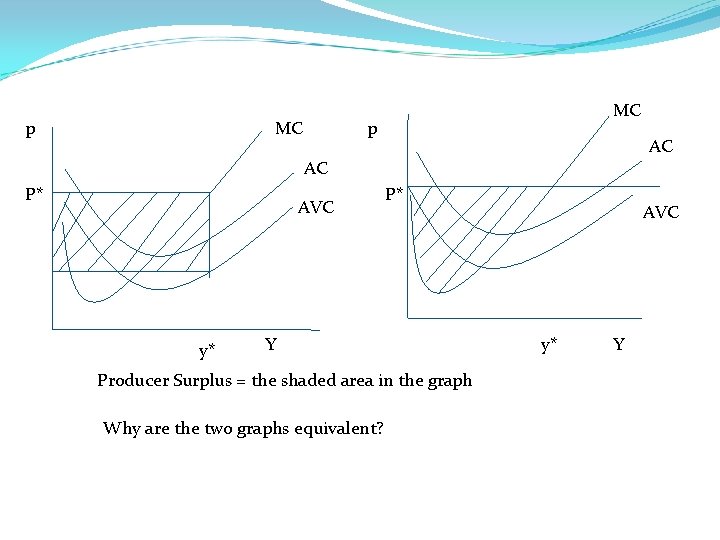
MC p AC AC P* AVC y* P* Y Producer Surplus = the shaded area in the graph Why are the two graphs equivalent? AVC y* Y

Why is Producer’s Surplus relevant if profit matters? In SR must be true that ∆PS=∆� Why? Fixed costs don’t change as y changes in SR L-R Supply Curve S-R Supply Curve = MC above AVC Where MR=MC P= MC (y, k) – k is fixed L-R Supply Curve = same with K variable => where MR = MC P = MC (y, k(y)) K is optimal

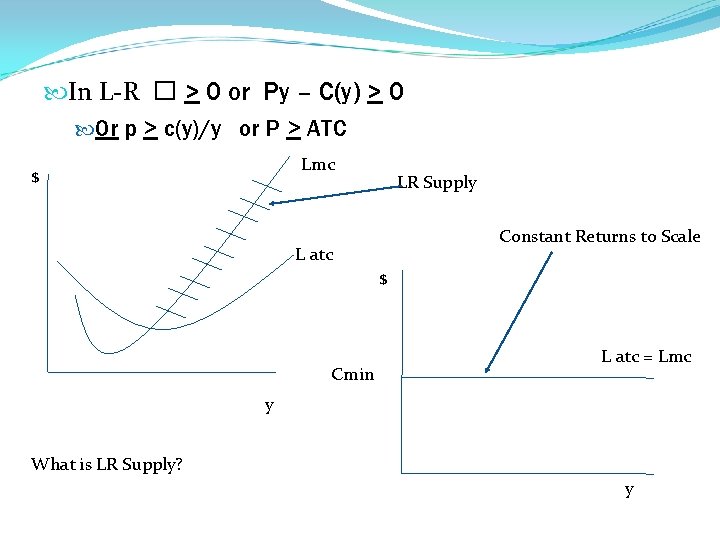
In L-R � > 0 or Py – C(y) > 0 Or p > c(y)/y or P > ATC Lmc $ LR Supply Constant Returns to Scale L atc $ Cmin L atc = Lmc y What is LR Supply? y

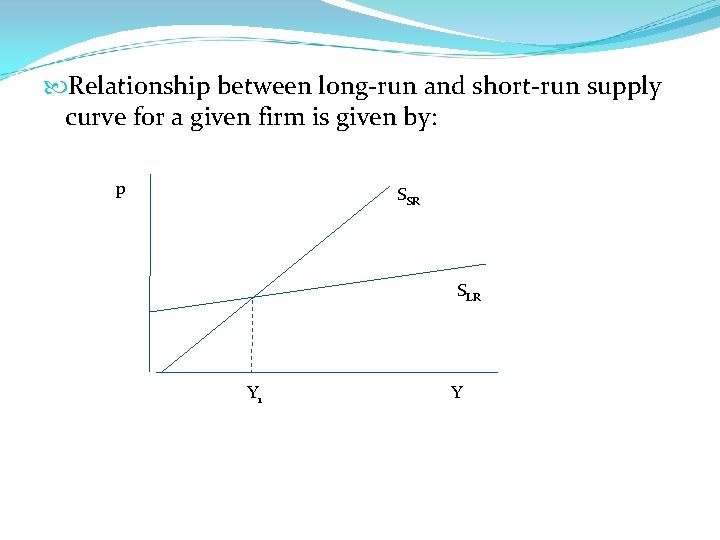
Relationship between long-run and short-run supply curve for a given firm is given by: p SSR SLR Y 1 Y

Why would SLR be more elastic (more responsive to price changes)? Can change both K & L optimally in the L-R => Increase y at lower cost beyond y 1 in the LR Note: (Producer Surplus)LR = �LR since all inputs are variable.

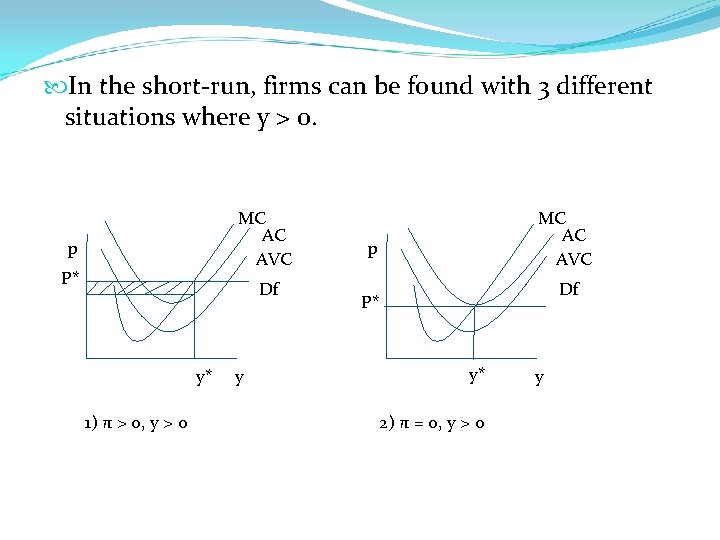
In the short-run, firms can be found with 3 different situations where y > 0. MC AC AVC p P* Df y* 1) π > 0, y > 0 y MC AC AVC p Df P* y* 2) π = 0, y > 0 y

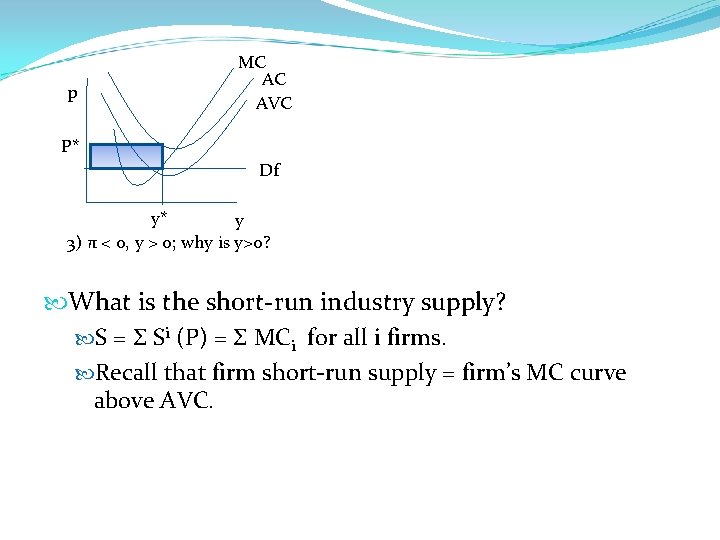
p MC AC AVC P* Df y* y 3) π < 0, y > 0; why is y>0? What is the short-run industry supply? S = Σ Si (P) = Σ MCi for all i firms. Recall that firm short-run supply = firm’s MC curve above AVC.

Long-Run Equilibrium in Perfect Competition No fixed inputs. Free entry and exit. Consider firms of type 3 above ( π < 0 but p > AVC) who still produce in short-run. What happens? No fixed costs => observe exit in the market and π rises to zero. Consider firms of type 1 above (π > 0). What happens? The positive π serves as a signal to other firms to enter => π falls to zero. The long equilibrium occurs where π equals 0. What does this look like, assuming all firms have the same costs?

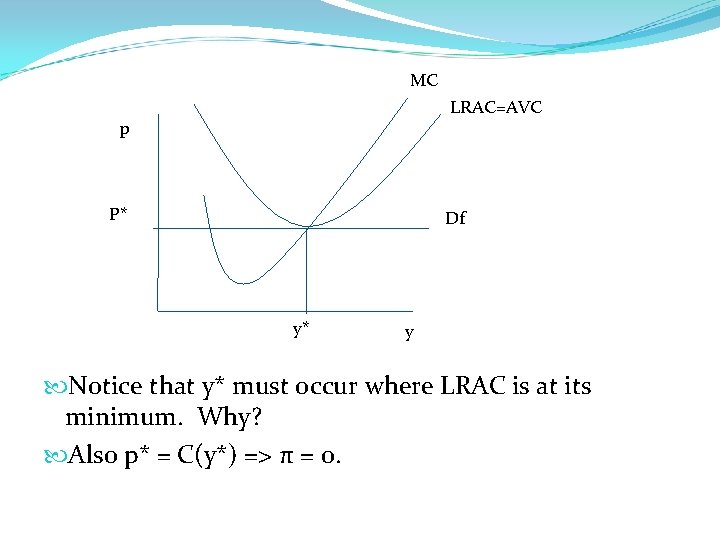
MC LRAC=AVC p P* Df y* y Notice that y* must occur where LRAC is at its minimum. Why? Also p* = C(y*) => π = 0.

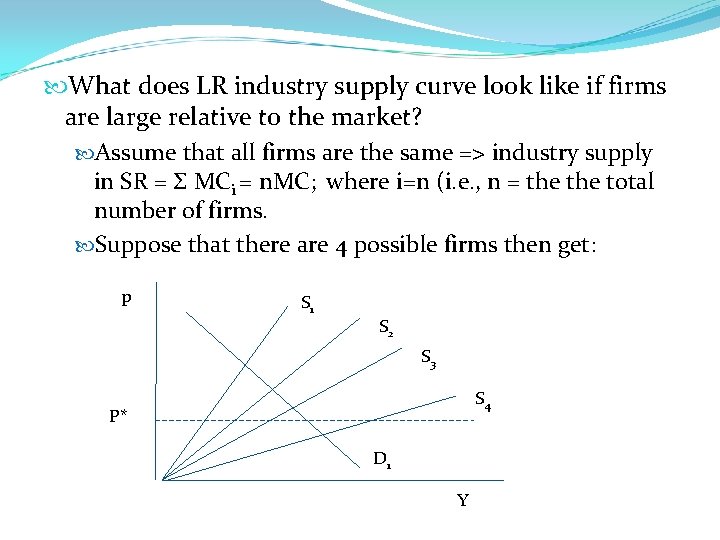
What does LR industry supply curve look like if firms are large relative to the market? Assume that all firms are the same => industry supply in SR = Σ MCi = n. MC; where i=n (i. e. , n = the total number of firms. Suppose that there are 4 possible firms then get: p S 1 S 2 S 3 S 4 P* D 1 Y

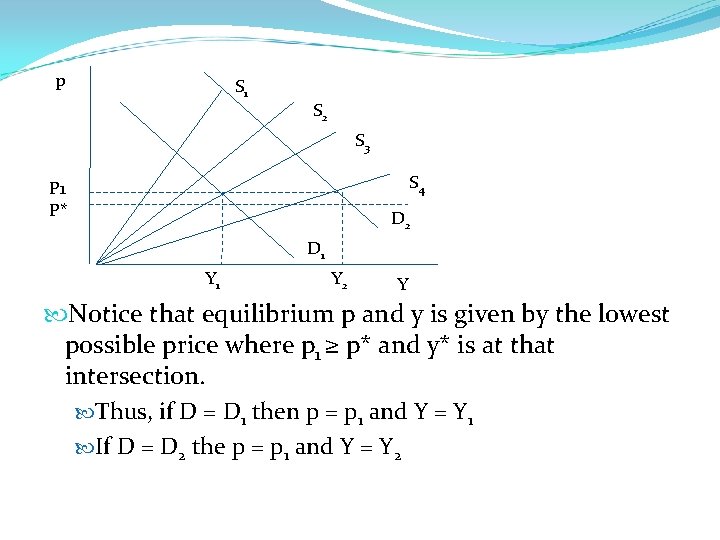
p S 1 S 2 S 3 S 4 P 1 P* D 2 D 1 Y 2 Y Notice that equilibrium p and y is given by the lowest possible price where p 1 ≥ p* and y* is at that intersection. Thus, if D = D 1 then p = p 1 and Y = Y 1 If D = D 2 the p = p 1 and Y = Y 2

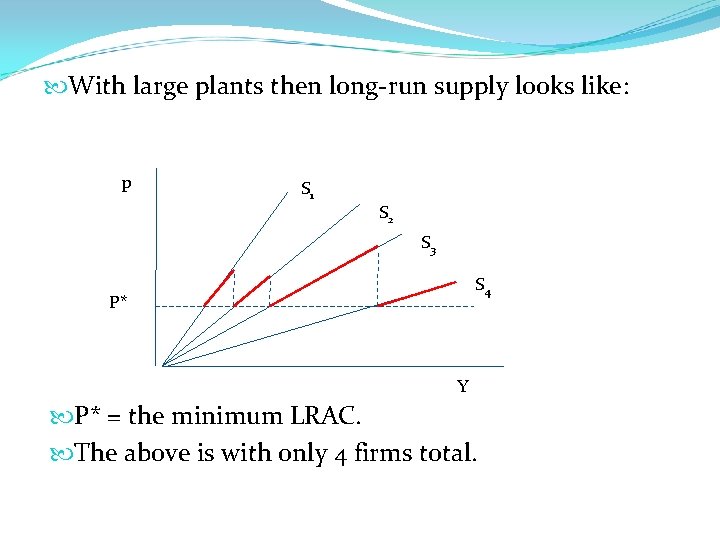
With large plants then long-run supply looks like: p S 1 S 2 S 3 S 4 P* Y P* = the minimum LRAC. The above is with only 4 firms total.

What if firms are all very small with respect to the market? p P* SLR = min LRAC Y

Taxes The graph below shows the SLR both before and after a tax is imposed. p P*+ tax P* SLR after tax SLR before tax Y

Where is the equilibrium? For that must have Demand SSR p P*+ tax P 1 P* SSR SLR after tax SLR before tax D Y Short-run Equilibrium is at P 1 therefore, both firms and consumers pay tax. Long-run Equilibrium is at P* + tax therefore only consumers pay tax in long-run.

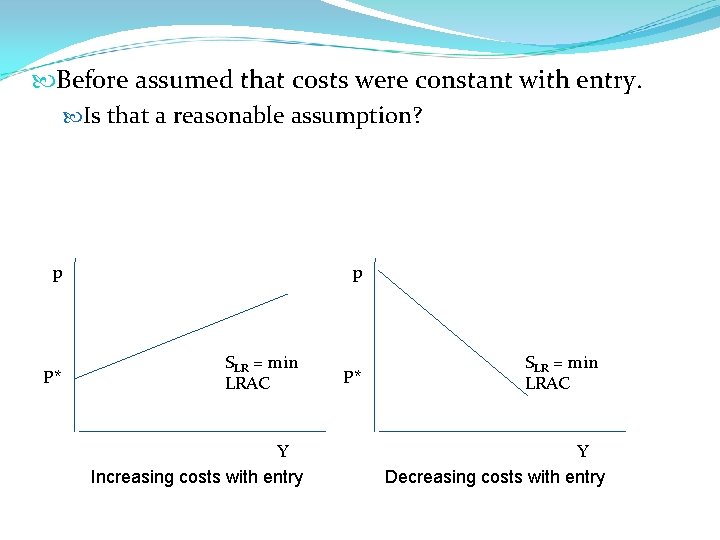
Before assumed that costs were constant with entry. Is that a reasonable assumption? p P* p SLR = min LRAC Y Increasing costs with entry P* SLR = min LRAC Y Decreasing costs with entry

Economic Rent Suppose that we look at the rent earned by a highly paid sports or entertainment individual. Do D and S still determine price? Yes. p S P* D Y

D and S still determine price but what economic rent is the player getting? That is, due to a talent restriction, there is no free entry for the players. Can profit be driven to zero under these conditions? Suppose fixed supply of Peyton Manning and his opportunity cost = $100, 000 but his MP in football = $10 m. Profits are driven to zero just for the firm producing the product (i. e. , NFL team). The economic rent is the payment for the fixed factor(s) = total fixed costs. What is rent seeking behavior?

What affects the size of the rent? Depends upon the fixed supply for the talent market (Peyton Manning) and the no-talent market (me). p S P* D D Y Talent Market Y No. Talent Market

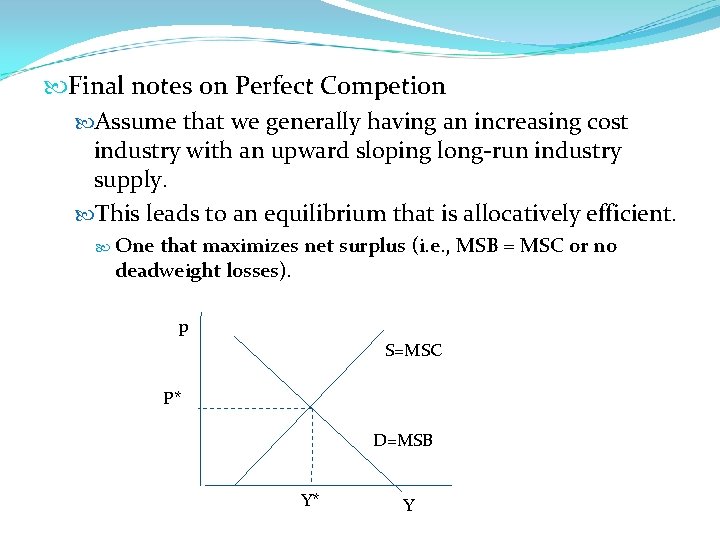
Final notes on Perfect Competion Assume that we generally having an increasing cost industry with an upward sloping long-run industry supply. This leads to an equilibrium that is allocatively efficient. One that maximizes net surplus (i. e. , MSB = MSC or no deadweight losses). p S=MSC P* D=MSB Y* Y