Advanced Inorganic Chemistry By Dr MAHMOUD NAJIM Lecture

Advanced Inorganic Chemistry By Dr. MAHMOUD NAJIM Lecture: Electronic Spectra of Coordinated Compounds

The way of how to analyze the electronic spectra of complexes improve our understanding of their bonding. First of all we shall start with the electronic spectra of atoms. Electronic Spectra of Atoms: Electronic configuration for elements give us an idea about the number of electrons in each orbital , but it doesn't give us the arrangements of electrons in atoms. For configuration 2 p 2, as an example, the two electrons might occupy any of p orbitals with different orientations which means that we may have several different states of total orbital angular momentum, and each on corresponds to an occupation of orbitals with different values of ml and ms and this case called microstates. For the notation s, p, d, …. for orbitals with l = 0, 1, 2, …. , the total orbital angular momentum of an atomic term is donated by the upper case equivalent : L = 0 1 2 3 4 ……. S P D F G ( then alphabetical omitting J ) The total spin quantum number (S ) of an atom is normally reported as the multiplicity of the term, the value of 2 S +1 : S = 0 ½ 1 1½ 2 …… 2 S +1 = 1 2 3 4 5 …… The process of combining electron angular momenta by summing first the spin, then the orbital momenta and finally the two resultants is called Russell – Saunders Coupling The multiplicity is written as a left superscript on the letter representing the value of L, and the entire label of a term is called a term symbol. Thus, the term symbol 3 P donates a term with L = 1 and S =1 an is called a triplet term.

Microstates that correspond to different relative spatial distributions of electrons have different energies. For 2 p 2, as an example, there are 15 possible microstates configurations, while for 3 d 2 there are 45 possible microstates ? , so we can conclude that the terms of a 3 d 2 configuration are 1 G, 3 F, 1 D, 3 P and 1 S which account for all 45 permitted states. The Pauli principle restricts the microstates that can occur in configuration, and consequently it affects the terms that can occur. The energies of the terms: For a given configuration, the values of S and L can be calculated and it is possible to predict the ground term by using Hund`s rules. There it was expressed as , the lowest energy configuration is achieved if the electrons are parallel, so we can write the following two statements ; 1 For a given configuration, the term with the greatest multiplicity lies lowest in energy. 2 For a term of given multiplicity, the greatest the value of L, the lower the energy. These two rules give us that, in 3 d 2 the configuration 3 F is lower in energy than 3 P, so for Ti+2 the ground term is 3 F. Hund`s rules are reasonably reliable for predicting which term has lower energy( the ground state), but are not very reliable for predicting the order in which terms of higher energy lie. Thus, for Ti+2 the rules predict the order 3 F < 3 P < 1 G < 1 D < 1 S but the observed order is 3 F < 1 D < 3 P < 1 G < 1 S

The spin multiplicity rule is fairly reliable for predicting the ordering of n terms, but the greatest L rule is reliable only for predicting the ground terms, there is generally little correlation of L with the order of the higher terms. The procedure for predicting the ground term of an atom or ion may be summarized as follows: 1 - Identify the microstate that has the highest value of multiplicity. 2 - Identify the highest permitted value of L for that multiplicity. Electronic Spectra of Complexes: The region for the electronic spectra of the complexes usually applied at the range 200 – 800 nm. For transition metal complexes we can identify a maximum of four types of transitions as follows: 1 Absorption bands attributed to π – π* and n – π* transitions for the organic part of the complexes( ligands), located at the ultraviolet region. 2 Absorption bands attributed to charge transfer transition ( metal to ligand or ligand to metal), located between last part of ultraviolet and first part of visible region. 3 Absorption bands attributed to d – d transition of the metal ion located at the visible region. 4 Absorption bands attributed to the counter ion ( if presents), located at the same area of the charge transfer absorption bands. Absorption bands for 1 and 2 seems to be very strong while it is medium for 4 and weak for 3, why? . Any complex should had two absorption bands ( 2 and 3) while some complexes could had the other two or one of them, why? .

Let us take the simplest possible case with a d 1 configuration, [Ti(H 2 O)6]+3 the d electron will occupy a t 2 g orbital. On irradiation with light of frequency c, equal to ∆o/h, where h is Plank`s constant. The d electron captured the quantum of radiation and excited from t 2 g to the eg orbital. The absorption bands found to be in the visible spectrum of complex and is responsible for the violet color. Three features of this absorption band are of importance, the position, the intensity and the breadth. Fig. 1 The position of the band is related to the splitting of the d orbitals, the spectrum tell us that ∆o in the complex is 20. 000 cm-1. Since there are 83. 7 cm-1 per kilojoules, that means the splitting energy is about 250 k. J per mole. The intensity of the absorption band is extremely weak compared to the other bands because the transition involved in this band is in the same orbital (d – d )and according to the Laporta`s rule it is forbidden ( in tetrahedral complexes the absorption band is greater with the factor 10* , why? ). The absorption band seems to be a broad band due to the vibration of the complex. Complexes with a d 9 configuration ( Cu. II) will have a same spectrum as d 1 although it is not simple as Ti( III) complex, several nearly superposed bands, due to the distortion of the octahedral complex ( Jahn – Teller effect).

Fig. 1 The visible absorption spectrum of [Ti(H 2 O)6]+3

Ti(III) is a d 1 complex and exhibits ONE absorption in its electronic spectrum due to transition of the electron from the t 2 g orbitals to the eg orbitals. The energy of the absorption corresponds to DO. Br– Cl– (H 2 N)2 C=O NCS– F– H 2 O CN– 11, 400 13, 000 17, 550 18, 400 18, 900 20, 100 22, 300

For complexes having more than one but less than nine electrons, we must employ an energy level diagram based upon the Russell – Saunders states of the relevant dn configuration in the free ( uncomplexed ) ion. It can be shown that just as the set of five d orbitals is split apart by the electrostatic field of surrounding ligands to give two or more sets of lower degeneracy, so also are the various Russell – Saunders states of a dn configuration. The number and types of the components into which an octahedral field will split a state of given L is the same regardless of the dn configuration from which it arises ( Table 1 ). Although the states into which a given free ion state is split are the same in number and type in both octahedral and tetrahedral field, the pattern of energies is inversed in one case relative to the other, why? . The electronic spectra of the complex [Cr(NH 3)6]+3 in aqueous solution showed two types of absorption bands, Fig. 1, The bands at the lowest energy attributed to d – d transition, while the very intense band attribute to charge transfer transition. A closer analysis shows that there is also a third transition hidden under the very intense CT band. The ground configuration for this complex is t 32 g so the excited state is t 22 geg 1 t 32 g ; because there are three t 2 g orbitals and two eg orbitals, there are in fact six possible transitions because any of the three t 2 g electrons can migrate to either of the two eg orbitals. In the absence of interelectron repulsions, all six transitions occur at the same energy. However, because there are interelectron repulsions, the transition energies depend on which orbitals are specially involved in the transition.

Table – 1 Russell – Saunders states in Oct. & Tet. Electronic field

Fig. 2 The spectrum of the d 3 complex [Cr(NH 3)6]+3

It may be helpful to see qualitatively from the viewpoint of simple MOT why there are two bands. The dz 2 dxy transition promotes an electron from the xy plane into the already electron rich z direction ( it is electron rich because both dyz and dxz are occupied). However, the dz 2 dxz transition merely relocates an electron that is already largely concentrated along the z axis , Fig. 3. The repulsion between electrons in these two cases are not the same, and as a result the two eg t 2 g transitions lie at different energies. All the other transitions resemble one or other of these two cases, and three transitions fall into one group and the other three fall into the second group. The spectrum of octahedral and tetrahedral complexes of Mn(II) in Mn(H 2 O)6]+2 and [Mn. Br 4]-2 showed for the first one, a very weak bands compared to other octahedral complexes and a large number of bands and last a great variation in the width of the bands, with one extremely narrow indeed( Fig. 4 ). The correspond to the 6 S ground state of the free ion, which is not split by the ligand field. All the excited states have different spin multiplicity from the ground state, and transition to them are spin forbidden. Because of weak spin orbit interaction, such transition are not totally absent, but they are very weak. Tetrahedral complexes of Mn(II) are yellow – green, and the color is more intense than that of the octahedral complexes. As shown in Fig. 4 the molar absorbance is 100 times than that of the octahedral due probably to the fact that in tetrahedral environment there is a mixing between p orbitals of the ligands and d orbital of the metal ion, which is facilitated by overlap of metal d orbitals with ligand orbitals in the tetrahedral complexes.

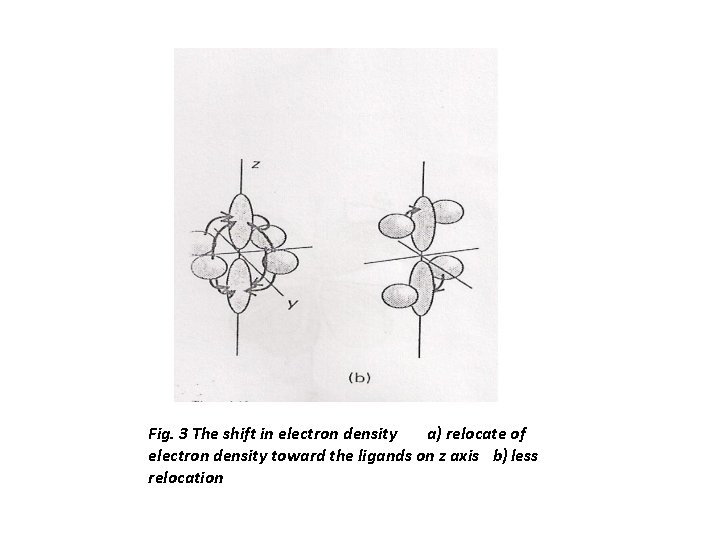
Fig. 3 The shift in electron density a) relocate of electron density toward the ligands on z axis b) less relocation

Fig. 4 The d – d absorption spectra of the Mn(H 2 O)6]+2 ion (solid) and the [Mn. Br 4]-2 ion ( dashed curve)