Speed of Light How fast is the speed

Speed of Light How fast is the speed of light? depends on the material (index of refraction) in vacuum, c = √ [1/ oεo] = 3 x 108 m/s What is this speed relative to? What is the speed of sound relative to? the ground? the air? the source? the receiver?

Speed of Light What is the speed of sound relative to? the ground? the air? the source? the receiver? For sound, it moves relative to the medium it is moving in: v = [B/ρ]1/2 , independent of the source and independent of the receiver. For light, from the E&M theory, where the sub 0’s indicate vacuum. So the speed of light must be relative to vacuum.

Speed of Light So how do we determine any speed relative to vacuum? Idea: try to measure speed of light on earth, then we can see how fast the earth is moving through vacuum. From the idea of relative speed, vresult = vin medium + vof medium (add as vectors). But the speed of light is so large! How do we find a relatively small difference in speeds between vresult and vin medium ?

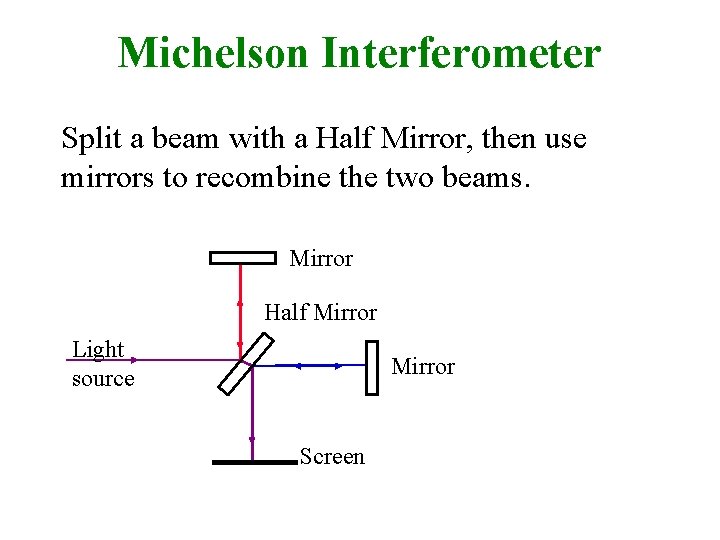
Speed of Light vresult = vin medium + vof medium The Michelson-Morley experiment used the Michelson interferometer in an attempt to find the speed of the earth through space, that is, by measuring the speed of light with respect to the earth, vresult, and knowing the speed of light in the medium, vin medium = c, we can determine the speed of earth through the vacuum, vof medium. Let’s first review the Michelson interferometer:

Michelson Interferometer Split a beam with a Half Mirror, then use mirrors to recombine the two beams. Mirror Half Mirror Light source Mirror Screen

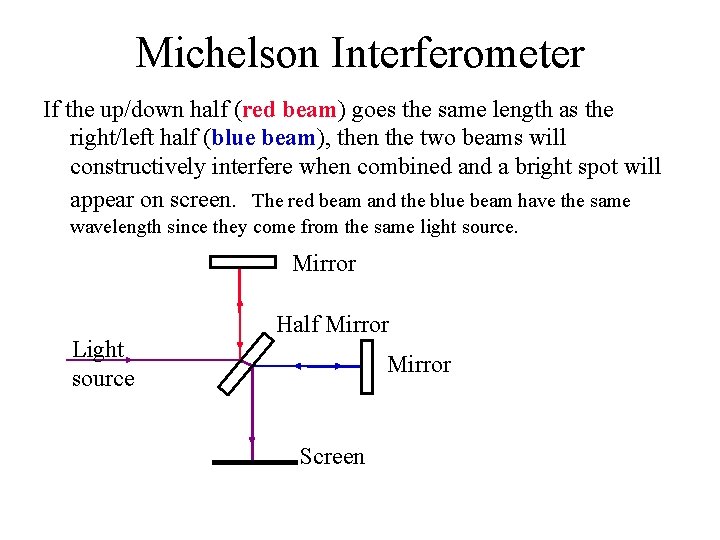
Michelson Interferometer If the up/down half (red beam) goes the same length as the right/left half (blue beam), then the two beams will constructively interfere when combined and a bright spot will appear on screen. The red beam and the blue beam have the same wavelength since they come from the same light source. Mirror Light source Half Mirror Screen

Speed of Light But that assumed the apparatus was stationary. Since light should travel with respect to space (rather than with respect to the source or the receiver or the earth), we need to consider the whole apparatus as moving (with the earth & sun through space). So the light will have to travel DIFFERENT PATHS for the two beams: the up/down half versus the left/right half as we show next:

Michelson Interferometer Here we are assuming the earth is moving to the right with respect to space. (c tup) = [L 2 + (ve tup)2]½ (c t. R) = L + ve t. R Dotted items are positions when light first hits the half mirror Mirror L Light source ve ve tup ct. R ve t. R Mirror L Half Mirror Screen

Michelson Interferometer (c tdown) = [L 2+(ve tdown)2]½ (c t. L) = L - vet. L Mirror ve tdown ctdown Half Mirror L ct. L L Screen ve t. L Mirror

Speed of Light (c tup) = [L 2 + (ve tup)2]½ ; (c t. R) = L + ve t. R (c tdown) = [L 2 + (ve tdown)2]½ ; (c t. L) = L - vet. L Note that tup = tdown by symmetry, but that t. R does NOT equal t. L due to the opposite direction of the light. We now solve for tup-down = tud = tup + tdown and for tright-left = t. RL = tright + tleft

Speed of Light (c tup) = [L 2 + (ve tup)2]½ (c tdown) = [L 2 + (ve tdown)2]½ tup-down = tud = tup + tdown = 2 tup so solving the first equation for tup gives: c 2 tup 2 = L 2 + (ve tup)2 , or tup 2(c 2 – ve 2) = L 2 , or tup = [L 2 /{c 2 - ve 2}]½ = L / {c 2 - ve 2}½ so tud = 2 L/{c 2 -ve 2}½ = 2 L/c * [1/{1 -(ve/c)2}½].

Speed of Light ct. R = L + vet. R and ct. L = L - vet. L , so t. R = L / (c - ve) and t. L = L / (c + ve) , so (getting a common denominator) t. RL = t. R + t. L = L*[(c+ve) + (c-ve)] / (c 2 - ve 2) (and dividing numerator and denominator by c 2) = 2 Lc / (c 2 - ve 2) = 2 L/c *[1 / {1 - (ve/c)2}]. Recall: tud = 2 L/c * [1/{1 -(ve/c)2}½]. Note that the two times are DIFFERENT. This should cause a difference in the interference pattern on the screen.

Speed of Light t. RL = 2 L/c * [1 / {1 - (ve/c)2}]. tud = 2 L/c * [1 / {1 - (ve/c)2}½]. Note that if ve = 0, then the two times are the SAME. Let’s see about the time difference if ve > 0. Which of the two times is bigger?

Speed of Light t. RL = 2 L/c * [1 / {1 - (ve/c)2}]. tud = 2 L/c * [1 / {1 - (ve/c)2}½]. The ve/c is less than one, so the denominator {1 - (ve/c)2} is also < 1. The square root of a fraction is bigger than the original fraction ( [¼]½ = ½ > ¼ , so [¼]½ > ¼ ). Since we are dealing with the denominator, the one with the square root (which is bigger) will be the smaller overall quantity. So tud < t. RL if ve > 0.

Speed of Light t. RL = 2 L/c *[1 / {1 - (ve/c)2}]. tud = 2 L/c * [1/ {1 - (ve/c)2}½]. t = t. RL - tud = [2 L/c]*{[1 / {1 - (ve/c)2}] - [1 / {1 - (ve/c)2}½]} use approximations that (for small x) 1/{1 - x} ≈ 1 + x and 1/{1 - x}½ ≈ 1 + x/2 so with x = (ve/c)2 we get: t ≈ (2 L/c)*(1/2)*(ve/c)2 = (L/c)*(ve/c)2. How big is this?

Speed of Light t = (L/c)*(ve/c)2. If we have L = 10 meters, and if ve = 3 x 104 m/s (due to earth’s speed around the sun), THEN t = (10 m / 3 x 108 m/s) * [(3 x 104 m/s)/(3 x 108 m/s)]2 = 3. 3 x 10 -8 sec * (1 x 10 -8) = 3. 3 x 10 -16 sec. Can we measure such a small time?

Speed of Light t = 3. 3 x 10 -16 sec If we consider the merits of the Michelson Interferometer, we can see that we can detect a fraction of a wavelength, and so we can detect a fraction of a period. The period for visible light, say = 500 nm, is f = c = T, or T = /c = 5 x 10 -7 m / 3 x 108 m/s = 1. 6 x 10 -15 sec.

Speed of Light With t = 3. 3 x 10 -16 sec, and T = 1. 6 x 10 -15 sec we have t / T = 0. 2. Thus we should see AT LEAST a fringe shift of 0. 2 , and probably more since we expect the sun to be moving through the galaxy, etc. , and the above 0. 2 shift is that due only to the earth orbiting about the sun.

Experimental Considerations Is it critical to have the two lengths exactly the same? No – having one length slightly different would not significantly affect the amount of the fringe shift. (To see this, replace L with L(1+ ) on one of the sides (with being very small), and see what affect this will have. ) How do we determine which is the up-down side and which is the left-right side? If we are able to rotate the apparatus through 90 o, we should see the fringe shift change from 0. 2 shifts to zero and then forward to 0. 2 shifts.

Speed of Light Michelson & Morley determined that their apparatus was sensitive to about 0. 01 shifts, and they expected NO LESS than 0. 20 shifts. RESULT: Michelson & Morley detected about 0. 01 shifts - a null result! Either the earth is stationary in the universe, (which we know it isn’t), or there is something wrong with our thinking!

Speed of Light Up to now, we have more or less assumed, maybe without thinking about it, that there is one best system with one absolute time. Einstein had a different thought: Einstein said: If all the laws of physics apply in all inertial frames (see next slide for explanation of inertial frames), why should the speed of light be different in all those inertial frames? Shouldn’t the speed of light also be the same in all inertial frames?

Inertial Reference Frames First a short discussion about inertial frames. Newton’s Second Law relates physically identifiable FORCES to ACCELERATIONS: F = ma. Any frame in which Newton’s Second Law holds without strange forces is called an inertial frame. Counter-examples may help make this clear. There are frames that are not inertial, but these frames have “strange” forces. We’ll show 2 examples of NONINERTIAL FRAMES: 1. an accelerating spaceship; 2. the earth’s rotating surface.

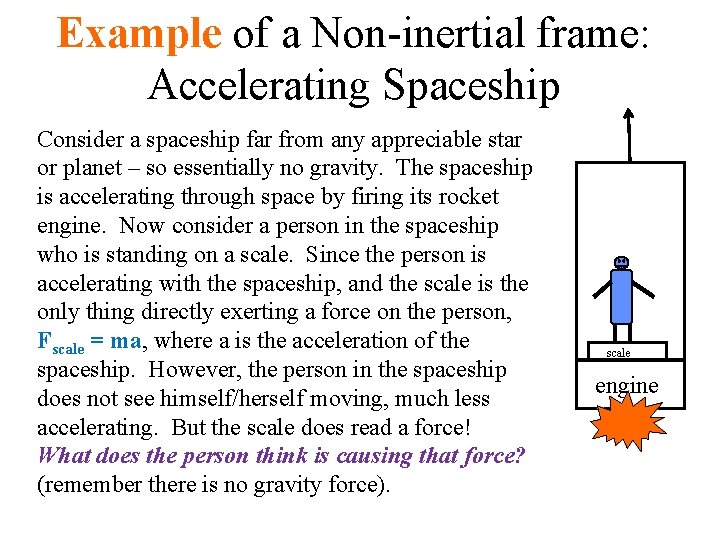
Example of a Non-inertial frame: Accelerating Spaceship Consider a spaceship far from any appreciable star or planet – so essentially no gravity. The spaceship is accelerating through space by firing its rocket engine. Now consider a person in the spaceship who is standing on a scale. Since the person is accelerating with the spaceship, and the scale is the only thing directly exerting a force on the person, Fscale = ma, where a is the acceleration of the spaceship. However, the person in the spaceship does not see himself/herself moving, much less accelerating. But the scale does read a force! What does the person think is causing that force? (remember there is no gravity force). scale engine

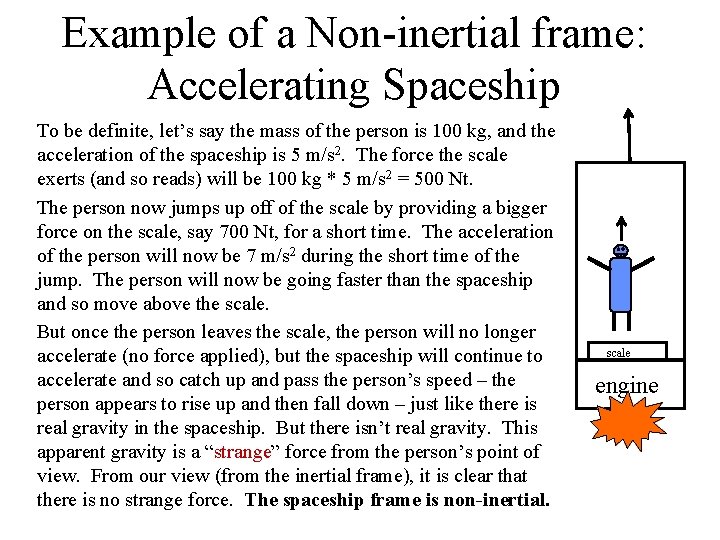
Example of a Non-inertial frame: Accelerating Spaceship To be definite, let’s say the mass of the person is 100 kg, and the acceleration of the spaceship is 5 m/s 2. The force the scale exerts (and so reads) will be 100 kg * 5 m/s 2 = 500 Nt. The person now jumps up off of the scale by providing a bigger force on the scale, say 700 Nt, for a short time. The acceleration of the person will now be 7 m/s 2 during the short time of the jump. The person will now be going faster than the spaceship and so move above the scale. But once the person leaves the scale, the person will no longer accelerate (no force applied), but the spaceship will continue to accelerate and so catch up and pass the person’s speed – the person appears to rise up and then fall down – just like there is real gravity in the spaceship. But there isn’t real gravity. This apparent gravity is a “strange” force from the person’s point of view. From our view (from the inertial frame), it is clear that there is no strange force. The spaceship frame is non-inertial. scale engine

Another example of a Non-inertial frame: Surface of the earth Consider low pressure systems. Why does the wind circle the low pressure area instead of just filling it in? We can answer that question nicely if we consider the earth from space:

Non-inertial Reference Frames Due to the rotating earth, the air South of the Low pressure system in the Northern Hemisphere is moving faster and will overshoot. The air North of the system is moving F slower and L F will fall behind.

Non-inertial Reference Frames From the earth’s surface, it looks like the air from the South has run around to the East of the system, and the air from the North has run around to the West - a counter-clockwise rotation. L

Non-inertial Reference Frames Thus from the earth’s surface, it looks like there is a strange force (called the Coriolis Force) acting. But from the space system, there is no need to invoke strange forces - it is clear that the result comes directly from known forces and Newton’s Second Law. Thus we can tell if our system is inertial or not - we simply see if we need “strange” forces. It is dangerous to try to walk on a merry-go-round when it is rotating due to the strange Coriolis force because this strange (apparent) force is quite large!

Inertial Reference Frames Any system that is moving with a constant speed relative to an inertial system is also an inertial system. This is true since acceleration is the CHANGE in velocity and does not depend on the amount of velocity. An example is that of riding in an airplane. As long as the ride is not bumpy and the plane is not accelerating (speeding up, slowing down, or turning), we do not realize that anything is different than on the ground!

Relativity If all the laws of physics hold in all inertial frames, then why (according to Einstein) should the speed of light be different inertial frames? But how could the speed of light be the same in two frames that are moving with respect to one another? How could that even be considered to be possible? - But then, why did the Michelson -Morley experiment give vearth = 0 ? We’ll see in the Introduction to the 1 st Relativity computer homework program how this works out.

Transformation Equations But before we do that, we need to consider how to transform from one inertial system to another. Consider the classical reasoning (which fails to explain the Michelson-Morley experiment): consider two inertial systems one moving at constant speed with respect to the other, call them the ground system and the airplane system. Caution: be extremely careful with knowing who is doing the measuring!

Galilean Transformation Eqs. Classical Reasoning An airplane passes over a ground observer at time 0 sec. This means that the position of the plane according to the ground observer is 0 m at 0 sec. (It also means that the ground observer’s position according to the plane is 0 m at 0 sec. ) We’ll consider that the plane is moving at some speed, v, to the right (+x direction) as seen by the ground observer. Notation: the first subscript on a quantity will be what is being measured followed by / and then who is doing the measuring. Example: position of a plane measured by a ground observer: xp/g

Galilean Transformation Eqs. plane xp/p = 0 m at t = 0 s vp/g Vp/g is the speed of the plane as measured by the ground observer. Note: xp/p will always be zero as t changes (xp/p means the x position of the plane as measured by the plane observer) xp/g = 0 m at t = 0 s Note: xp/g will increase with time: xp/g = vp/gt (xp/g means the x position of the plane as measured by the ground observer) xg/p = 0 m at t = 0 s Note: xg/p will decrease with time: xg/p = vg/pt = -vp/gt (xg/p means the x position of the ground observer as measured by the plane ground observer xg/g = 0 m at t = 0 s Note: xg/g will always be zero as t changes observer) (xg/g means the x position of the ground observer as measured by the ground observer)

Galilean Transformation Eqs. Since the plane is moving to the right, this would mean that the ground observer is moving to the left as seen from the plane. Note: vplane by ground = vp/g, and vground by plane = vg/p = -vp/g. Since the plane is moving at a constant speed, we can say: xof plane as seen by ground = xp/g = vp/g*t, and xof ground obs. as seen by plane = xg/p = vg/p*t = -vp/g*t. If something happens (event 1) in the plane’s system, say x 1/p in front of the plane at time t 1 , then the ground observer will say that the event happened at: x 1/g = x 1/p + vp/g*t 1.

Galilean Transformation Eqs. plane vp/g 1 xp/p = 0 m at t > 0 s xg/p = vg/p*t = -vp/g*t x 1/p xp/g = vp/g*t ground xg/g = 0 m at t > 0 s x 1/g xp/g = vp/g*t Recall that vp/g= -vg/p

Galilean Transformation Eqs. x 1/g = x 1/p + vp/g*t This is the Gallilean Transformation Equation. The inverse relation is: x 1/p = x 1/g + vg/p*t or x 1/p = x 1/g – vp/g*t If something is moving in the plane’s system, then we have: dx 1/g/dt = d(x 1/p+vp/gt)/dt , or v 1/g = v 1/p + vp/g and v 1/p = v 1/g + vg/p Since vg/p = -vp/g , the 2 nd eq. becomes v 1/p = v 1/g – vp/g , (where vp/g is the speed of the plane itself, v 1/g is the speed of the object as seen by ground, and v 1/p is the speed of the object as seen by the plane).

Galilean Transformation Eqs. x 1/g = x 1/p + vp/g*t, t 1/g = t 1/p= t, and v 1/g = v 1/p + vp/g , and the inverse transformation equations: x 1/p = x 1/g + vg/p*t, t 1/p = t 1/g = t, and v 1/p = v 1/g + vg/p or x 1/p = x 1/g - vp/g*t, and v 1/p = v 1/g – vp/g. remembering that vp/g = -vg/p. Even though there are different position and velocity measurements in the two systems, it is assumed that there is only one time measurement, t, so t 1/g = t 1/p = t. This may sound strange to point out since it seems like this would have to be the case.

Galilean Transformation Eqs. x 1/g = x 1/p + vp/g*t, t 1/g = t 1/p= t, and v 1/g = v 1/p + vp/g , and the inverse transformation equations: x 1/p = x 1/g + vg/p*t, t 1/p = t 1/g = t, and v 1/p = v 1/g + vg/p or x 1/p = x 1/g - vp/g*t, and v 1/p = v 1/g – vp/g. remembering that vp/g = -vg/p. The velocity equation was the basis for the prediction in the Michelson-Morley experiment: vresult = vin medium + vof medium (add as vectors) which did not agree with the experiment’s results! A new set of transformation equations are necessary if we are to explain the results of the Michelson-Morley experiment.

Lorentz Transformation Eqs. The derivation of these equations is done in PHYS 347. I will now use subscripts for earth and spaceship (e, s) instead of ground and plane (g, p). An Event or Object (o) happens in system e at xo/e, to/e and in system s at xo/s, to/s. The requirement is that if vo/e = c, then vo/s = c also. The object in this case would be a photon, i. e. , light going at a speed c. LTE’s: xo/e = (xo/s + vs/e*to/s) / [1 -(v/c)2]½ to/e = (to/s + vs/e*xo/s/c 2) / [1 -(v/c)2]½ here vs/e = - ve/s and v 2 = vs/e 2 = ve/s 2

Lorentz Transformation Eqs. LTE’s: xo/e = (xo/s + vs/e*to/s) / [1 -(v/c)2]½ to/e = (to/s + vs/e*xo/s/c 2) / [1 -(v/c)2]½ here vs/e = - ve/s and v 2 = vs/e 2 = ve/s 2 Note that the different frames will measure different locations and different times for the same event! THIS IS CRUCIAL! • Note that the only difference between the classical GTE and the LTE for the x equation is the inclusion of the denominator. The time equation is similar to the x equation. • Note that as (v/c) → 0, the LTE equations become the Galilean Transformation Equations.

Lorentz Transformation Eqs. LTE’s: xo/e = (xo/s + vs/e*to/s) / [1 -(v/c)2]½ to/e = (to/s + vs/e*xo/s/c 2) / [1 -(v/c)2]½ here vs/e = - ve/s and v 2 = vs/e 2 = ve/s 2 UNITS: note that in the x equation, the vs/e*to/s term has units of distance; and in the time equation, the vs/e*xo/s/c 2 term has units of time. The denominator in both equations, [1 -(v/c)2]½, is dimensionless.

Note on direction of vs/e in LTE’s: xo/e = (xo/s + vs/e*to/s) / [1 -(v/c)2]½ to/e = (to/s + vs/e*xo/s/c 2) / [1 -(v/c)2]½ here vs/e = - ve/s and v 2 = vs/e 2 = ve/s 2 To determine whether vs/e is positive or negative in the LTE, simply ignore the denominator and consider the regular (Galilean) transformation for position: xo/e = xo/s + vs/et If s is moving to the right with respect to e, then vs/e is positive since as time increases the position of s will become further to the right; if s is moving to the left with respect to e, then vs/e is negative since as time increases the position of s will become further to the left. Use the same sign for vs/e in the t equation as you do in the x equation.

Generalizing the LTE’s: xo/e = (xo/s + vs/e*to/s) / [1 -(v/c)2]½ to/e = (to/s + vs/e*xo/s/c 2) / [1 -(v/c)2]½ here vs/e = - ve/s and v 2 = vs/e 2 = ve/s 2 The example we’ve been using is transforming from spaceship xs and ts into earth xe and te values. If we want to go from earth to spaceship, simply replace the subscripts – but be careful to reverse vs/e to ve/s which means you will use the opposite sign since ve/s = -vs/e. We can also replace s and e with any two observers who are in inertial frames moving at constant speed relative to the other.

Simultaneity One of the most important consequences of the results of the Michelson-Morley experiment and the resulting LTE’s is the fact that observers in different inertial frames will NOT agree on whether two events at different places are simultaneous. This is demonstrated in the Introduction to the 1 st computer homework program on Relativity, Volume 6 #1. This problem with simultaneity will result in disagreements about not only timing measurements but distance and mass measurements as well!