Rappresentazione di dati numerici Sistemi numerici Si suddividono

Rappresentazione di dati numerici

Sistemi numerici • Si suddividono in: Non posizionali : quali ad esempio il sistema di numerazione romano (i cui simboli sono: I, III, IV, V, X, L, C, D, M) oppure quello egiziano Posizionali : quali ad esempio il sistema arabo (decimale) e il sistema maya (ventesimale). • Nei sistemi posizionali le operazioni aritmetiche risultano molto agevoli mentre in quelli non posizionali sono alquanto complicate. © Piero Demichelis 2

Sistema posizionale a base fissa • Nei sistemi numerici a base fissa, un numero N può essere rappresentato in uno del seguenti modi: N = dn 1; dn 2. . . . d 1; d 0; d 1. . . . d m N = dn 1· rn 1 +. . . + d 0· r 0 + d 1· r 1 +. . . + d m· r m © Piero Demichelis 3

Sistemi numerici • Proprietà di un sistema numerico a base fissa è a rango illimitato : ogni numero intero vi può essere rappresentato; è a rappresentazione unica : ad ogni numero intero corrisponde un solo insieme ordinato di cifre; è irridondante : ad ogni insieme ordinato di cifre corrisponde un solo numero non rappresentato da altri insiemi ordinati. © Piero Demichelis 4

Sistema decimale • r = 10 • cifre: { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 } Esempio: 10110 = 1 × 102 + 0 × 101 + 1 × 100 = 100 + 1 = 10110 © Piero Demichelis 5

Sistema binario • r = 2 • cifre: { 0, 1 } Esempio: 1012 = 1 × 22 + 0 × 21 + 1 × 20 = 4 + 0 + 1 = 510 © Piero Demichelis 6

Sistema ottale • r = 8 • cifre: { 0, 1, 2, 3, 4, 5, 6, 7 } Esempio: 1018 = 1 × 82 + 0 × 81 + 1 × 80 = 64 + 0 + 1 = 6510 • molto utile per scrivere in modo compatto i numeri binari (ad ogni 3 cifre binarie corrisponde una cifra ottale) ( 1 1 0 0 0 1) 2 = ( 6 1 ) 8 © Piero Demichelis 7

Sistema esadecimale • r = 16 • cifre: { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F } Esempio: 101 H = 1 × 162 + 0 × 161 + 1 × 160 = 256 + 0 + 1 = 25710 • anch’esso utile per scrivere in modo compatto i numeri binari (ad ogni 4 cifre binarie corrisponde 1 cifra esadecimale) ( 1 1 0 1 1 0 0 0 1) 2 = ( 1 B 1 ) 16 © Piero Demichelis 8

Sistema base 5 • r = 5 • cifre: { 0, 1, 2, 3, 4 } Esempio: 1015 = 1 × 52 + 0 × 51 + 1 × 50 = 25 + 0 + 1 = 2610 © Piero Demichelis 9

Sistema binario • Caratteristiche su n cifre si rappresentano 2 n numeri; ad esempio su 4 cifre: 0 1 10 11 100 101 110 111 . . . 0 1 2 3 4 5 6 7 1000 1001 1010 1011 1100 1101 1110 1111 . . . 8 9 10 11 12 13 14 15 Prime 16 potenze del 2: 20 21 22 23 24 25 26 27 28 . . . 1. . . 2. . . 4. . . 8. . . 16. . . 32. . . 64. . . 128. . . 256 © Piero Demichelis 29 210 211 212 213 214 215 216 . . . 512 . . . 1024 . . . 2048 . . . 4096 . . . 8192 . . . 16384. . . 32768. . . 65536 10

Sistema binario • La cifra binaria è detta bit parola che deriva dall’unione di due elisioni: binary digit • I bit estremi di un numero binario si chiamano: 1 0 1 1 1 0 0 MSB LSB (Most Significant Bit) (Least Significant Bit) © Piero Demichelis 11

Limiti del sistema binario • Poiché su n bit si rappresentano 2 n numeri, per rappresentare la stessa grandezza occorrono molte più cifre rispetto al sistema numerico decimale. bit simboli 4 8 16 32 val. minimo val. massimo 16 0 15 256 0 255 65, 536 0 4, 294, 967, 296 65, 535 0 4, 294, 967, 295 © Piero Demichelis 12

Conversione da binario a decimale • Si applica direttamente la definizione effettuando la somma pesata delle cifre binarie: 1012 = 1 × 22 + 0 × 21 + 1 × 20 = 4 + 0 + 1 = 5 1101. 12 = 1 × 23 + 1 × 22 + 0 × 21 + 1 × 20 + 1 × 2 1 = 8 + 4 + 0 + 1 + 0. 5 = 13. 510 © Piero Demichelis 13

Conversione da binario a decimale (2) B) Metodo consigliato: da mettendo in evidenza i fattori comuni, si ricava: © Piero Demichelis 14

Conversione da binario a decimale (3) Si deduce il seguente algoritmo: 1. 2. 3. 4. Si parte dalla cifra più significativa Si moltiplica per la base Si somma la cifra successiva Si ripete da 2. fino ad arrivare a d 0 Esempio: 10102 = ((1*2+0)*2+1)*2+0 = 1010 © Piero Demichelis 15

Conversione da decimale a binario N = dn 1· rn 1 +. . . + d 0· r 0 + d 1· r 1 +. . . + d m· r m • Consideriamo la sola parte intera e riscriviamo il numero binario nel modo seguente: N = d 0 + 2 · (d 1 + 2 · (d 2 +. . . + dn 1)) • Si può osservare che dividendo N per la base 2, si ottiene un quoziente (d 1 + r · (d 2 +. . . + dn 1)) e un resto d 0, che costituisce proprio la cifra meno significativa del numero nella base 2. • Dividendo successivamente il quoziente per la base 2 si trova ancora un quoziente e un resto d 1, che è la cifra di peso uno cercata, e così via. © Piero Demichelis 16

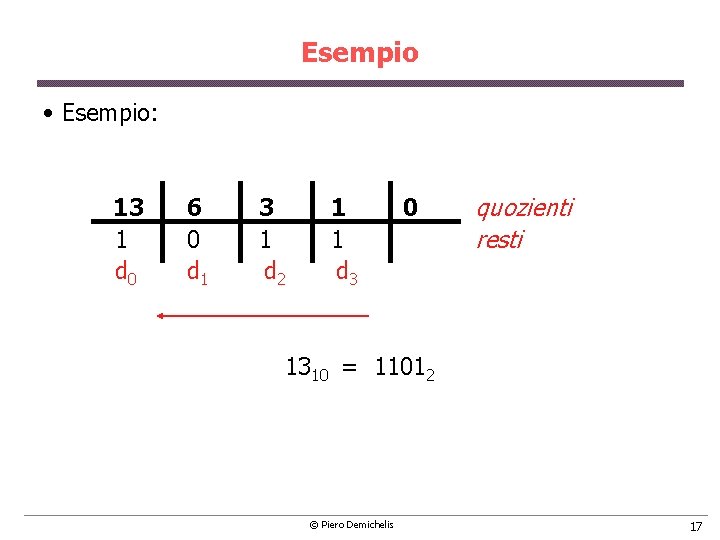
Esempio • Esempio: 13 1 d 0 6 0 d 1 3 1 d 2 1 1 d 3 0 quozienti resti 1310 = 11012 © Piero Demichelis 17

Numero di bit della rappresentazione binaria Problema: dato N 10, quanti bit (n) occorrono per rappresentarlo in base 2 ? Con n bit il massimo numero rappresentabile è: Con n 1 bit il massimo numero rappresentabile è: © Piero Demichelis 18

Numero di bit della rappresentazione binaria (2) Pertanto per rappresentare un numero x tale che x 2 n 1 e x > 2 n 1 1 occorrono n bit. Esempio: 3=22 1 < 5 < 7=23 1: 5 si rappresenta su 3 bit (infatti 510 = 1012). Ora: 2 n 1 1 < x 2 n 1 < x+1 2 n n 1 < log 2(x+1) n © Piero Demichelis 19

Numero di bit della rappresentazione binaria (3) n = log 2 (x+1) k = intero superiore o uguale a k In generale, per una base r: n = logr (x+1) © Piero Demichelis 20

Numero di bit della rappresentazione binaria (4) Dato N, il rapporto tra cifre decimali e bit occorrenti per rappresentarlo: D / B = log 10(N+1) / log 2(N+1) non è costante al variare di N. Si può però osservare che: 210 = 1024 1000 = 103 10 bit ogni 3 cifre decimali. Questo rapporto si mantiene per un largo intervallo di valori. © Piero Demichelis 21

Numero di bit della rappresentazione binaria (5) 210 = 1024 103 → Kilo 220 = 1. 048. 576 106 → Mega 230 = 1. 073. 741. 824 109 → Giga © Piero Demichelis 22

Conversione da decimale a binario • Dato un numero frazionario: N = a 1 2 1 + a 2 2 2 +. . . + a m 2 m • moltiplicando N per la base 2, si ricava come parte intera la cifra a 1, cioè la prima cifra binaria. • Eliminata questa parte intera, moltiplicando quanto resta ancora per 2, si ricava come parte intera a 2, ecc. • Le parti intere, scritte nel medesimo ordine con cui sono state ricavate, rappresentano il numero frazionario binario cercato. © Piero Demichelis 23

Esempio • Regola: si moltiplica per due la parte frazionaria e si prende la cifra intera prodotta dal risultato proseguendo fino alla precisione richiesta. Esempio: 0. 34 x 2 0. 68 x 0. 3410 = 0. 01012 1. 36 x 2 0. 72 x 2 1. 44 ecc. 13. 3410 = 1101. 01012 © Piero Demichelis 24

Per convertire un numero con parte intera e parte frazionaria, si convertono separatamente le due parti e poi si giustappongono. Esempio: 25. 812510 = (? )2 2510 = 110012 (metodo delle divisioni successive) 0. 812510 = 0. 11012 (metodo dei prodotti successivi) 25. 812510 = (11001. 1101)2 © Piero Demichelis 25

Conversioni tra sistemi in base qualsiasi • E’ ovvio che le regole di conversione decimale binario sono del tutto generali e valgono qualsiasi siano i sistemi numerici coinvolti. • Ad esempio per convertire il numero decimale 365 in base 7 si divide per 7: 365 52 7 1 0 1 3 0 1 36510 = 10317 © Piero Demichelis 26

Operazioni aritmetiche • Le operazioni aritmetiche in un qualsiasi sistema numerico si possono eseguire nello stesso identico modo che conosciamo così bene per il sistema numerico decimale. • L’avvertenza è solo quella di costruire la “tabellina” opportuna per quel particolare sistema numerico: si ricordi che la tabellina per il sistema numerico decimale ce la siamo studiata a memoria sin dall’infanzia!!!! • Il nostro interesse è però particolarmente concentrato sul sistema numerico binario e sono proprio le operazioni aritmetiche in binario che affronteremo ora. © Piero Demichelis 27

Somma in binario • Regole base: 0 + 0 = 0 + 1 = 1 + 0 = 1 + 1 = 0 1 1 0 con riporto (carry) di 1 • Si effettuano le somme parziali tra i bit dello stesso peso, propagando gli eventuali riporti: 1 1 0 1 1 0 + 6 + 0 1 1 1 = 7 = 1 1 0 1 13 © Piero Demichelis 28

Somma completa • La somma completa (full addition) tiene conto del riporto per cui si sommano due bit ed un carry ottenendo come risultato un bit di somma e un bit di riporto A B Carry S Rip 0 0 0 1 0 1 0 0 1 1 0 0 1 1 1 1 © Piero Demichelis 29

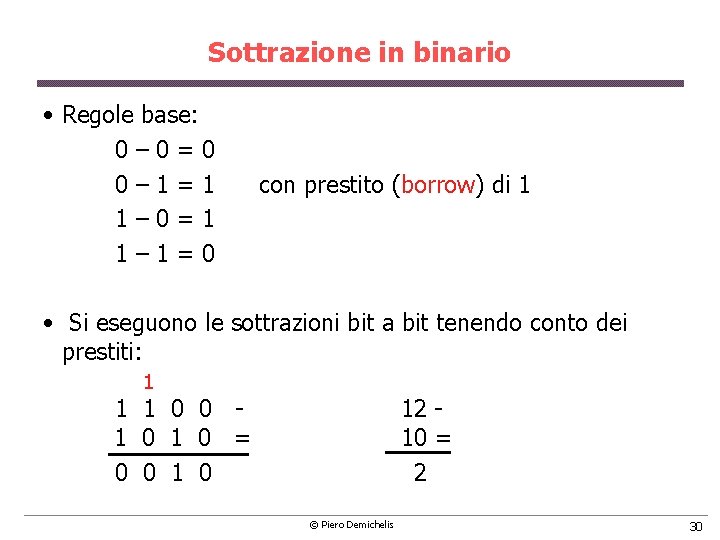
Sottrazione in binario • Regole base: 0 – 0 = 0 0 – 1 = 1 1 – 0 = 1 1 – 1 = 0 con prestito (borrow) di 1 • Si eseguono le sottrazioni bit a bit tenendo conto dei prestiti: 1 1 1 0 0 12 1 0 = 10 = 0 0 1 0 2 © Piero Demichelis 30

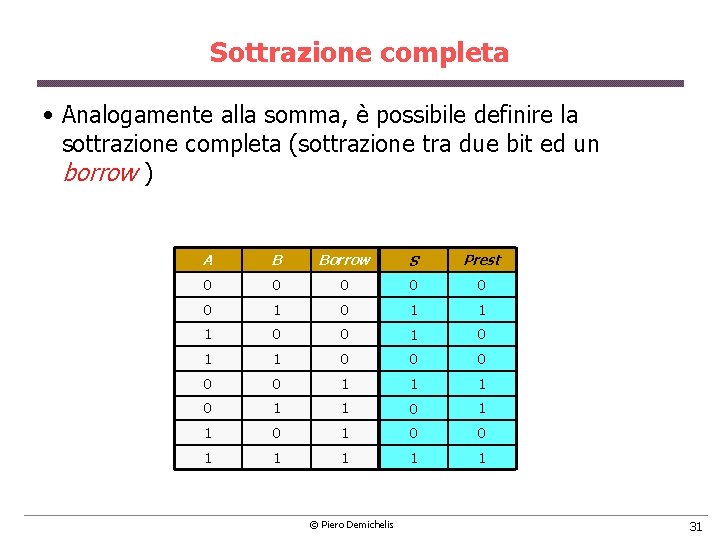
Sottrazione completa • Analogamente alla somma, è possibile definire la sottrazione completa (sottrazione tra due bit ed un borrow ) A B Borrow S Prest 0 0 0 1 0 1 1 1 0 0 0 1 1 1 0 0 1 1 1 © Piero Demichelis 31

Moltiplicazione in binario • Il prodotto tra due numeri binari si può calcolare con la tecnica già nota per i numeri in base 10, detta della somma e scorrimento. Esempio: 1 0 1 1 x 11 x 1 0 1 = 5 = 1 0 1 1 55 0 0 1 0 1 1 1 • Nella pratica si usano accorgimenti particolari basati sull’operazione di scorrimento (shift ). © Piero Demichelis 32

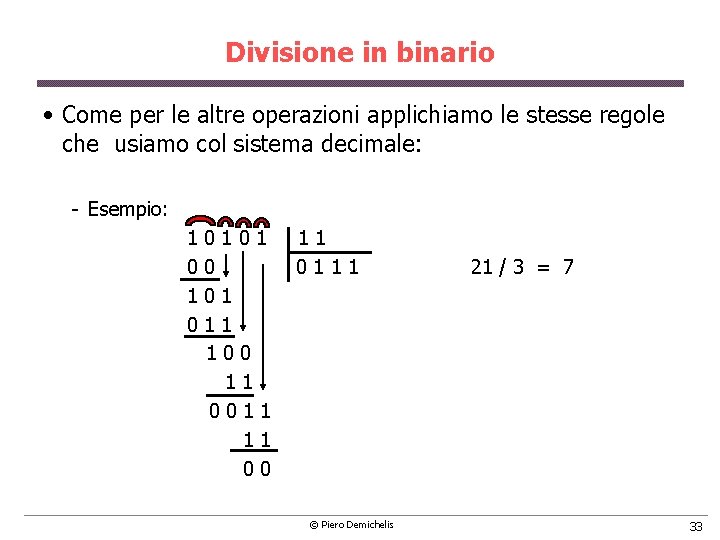
Divisione in binario • Come per le altre operazioni applichiamo le stesse regole che usiamo col sistema decimale: Esempio: 1 0 1 1 1 0 0 0 1 1 1 21 / 3 = 7 1 0 1 1 1 0 0 1 1 0 0 1 1 0 0 © Piero Demichelis 33

L’operazione di shift • Equivale ad una moltiplicazione o divisione per la base. • Consiste nel “far scorrere ” i bit (a sinistra o a destra) inserendo opportuni valori nei posti lasciati liberi. • In decimale equivale a moltiplicare (shift a sinistra) o dividere (shift a destra) per 10. • In binario equivale a moltiplicare (shift a sinistra) o dividere (shift a destra) per 2. © Piero Demichelis 34

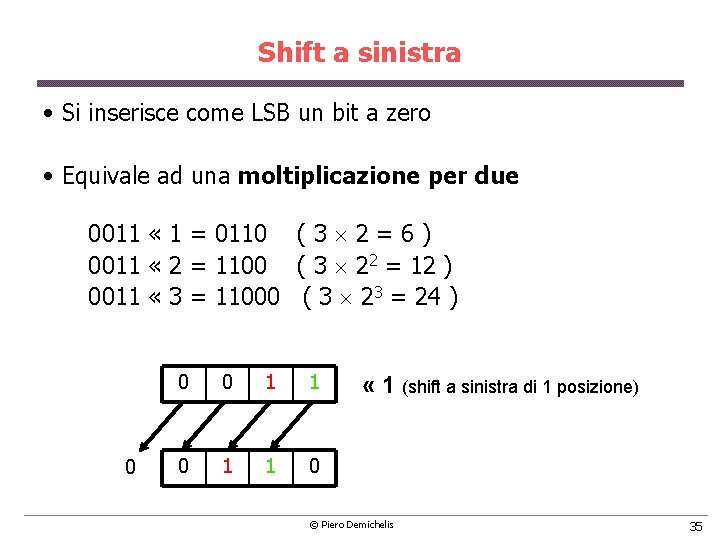
Shift a sinistra • Si inserisce come LSB un bit a zero • Equivale ad una moltiplicazione per due 0011 « 1 = 0110 ( 3 ´ 2 = 6 ) 0011 « 2 = 1100 ( 3 ´ 22 = 12 ) 0011 « 3 = 11000 ( 3 ´ 23 = 24 ) 0 0 0 1 1 0 « 1 (shift a sinistra di 1 posizione) © Piero Demichelis 35

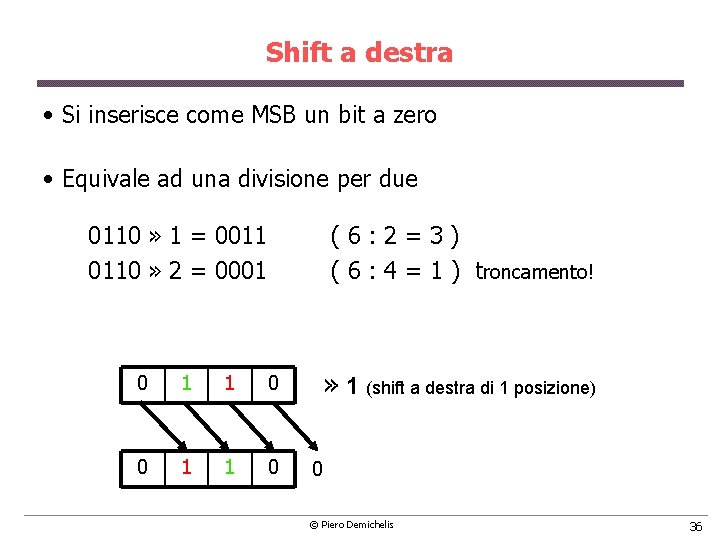
Shift a destra • Si inserisce come MSB un bit a zero • Equivale ad una divisione per due 0110 » 1 = 0011 0110 » 2 = 0001 ( 6 : 2 = 3 ) ( 6 : 4 = 1 ) troncamento! 0 1 1 0 » 1 (shift a destra di 1 posizione) 0 © Piero Demichelis 36

Moltiplicazioni • Una qualsiasi moltiplicazione tra due numeri può essere trasformata in una serie di shift e di somme, operazioni che vengono eseguite molto velocemente dai microprocessori. • Ad esempio il prodotto 14 x 13 diventa: 14 · 13 = 14 · (8 + 4 + 1) = 14 · 8 + 14 · 4 + 14 · 1 1410 = 11102 1 1 1110000 + 1110 « 3 + 1110 « 2 + 1110 111000 + 1110 = 10110110 © Piero Demichelis 37

Limiti della rappresentazione • Quando scriviamo sulla carta non ci preoccupiamo quasi mai della grandezza dei numeri (a meno di particolari necessità). • Nelle macchine numeriche un numero deve essere rappresentato in un particolare dispositivo elettronico interno che si chiama registro ed è paragonabile ad una cella di memoria. • Caratteristica fondamentale di questo dispositivo è la sua dimensione (numero di bit) stabilita in sede di progetto: ovvero in un elaboratore potremo rappresentare solo una quantità limitata di numeri. © Piero Demichelis 38

Limiti della rappresentazione • Ad esempio se il nostro contenitore (registro) è lungo 5 bit: potremo rappresentare solamente i numeri binari compresi tra 0 0 0 0 e 31 1 1 1 • Inoltre dovremo in qualche modo introdurre il segno dei numeri! © Piero Demichelis 39

I numeri con segno • Oltre al problema relativo al valore del numero bisogna trovare il modo di rappresentare il segno. • Il segno dei numeri può essere solo di due tipi: positivo ( + ) negativo ( ) • Sembrerebbe quindi facile rappresentarlo in binario, tuttavia la soluzione più semplice (1 bit riservato al segno) non è sempre conveniente. • Per tener conto del segno anziché il sistema numerico binario si utilizzano dei codici binari che hanno tuttavia come base, ovviamente, il sistema numerico binario. © Piero Demichelis 40

Modulo e segno • Su N bit, un bit è destinato al segno (in binario 0 = +, 1 = ) e N 1 bit al valore assoluto (anche detto modulo) S modulo • E’ un codice che ricorda molto il nostro modo di rappresentare i numeri sulla carta. • Presenta però gravi svantaggi dovuti alla doppia rappresentazione dello zero (esistono e sono leciti infatti sia + 0, che 0) e alla complessità delle operazioni aritmetiche. © Piero Demichelis 41

Modulo e segno • Esempi usando una codifica su quattro bit: + 310 0011 MS - 310 1011 MS • Si ha una doppia rappresentazione dello zero: 0000 MS + 010 1000 MS - 010 • In generale su N bit sono rappresentabili i valori: ( 2 N 1 1 ) x + ( 2 N 1 1 ) 8 bit 16 bit => [ 127 ÷ +127 ] [ 32. 767 ÷ +32. 767 ] © Piero Demichelis 42

Complemento a 1 • Considerando numeri binari di n bit, si definisce complemento a uno di un numero A la quantità: A = 2 n 1 – A • Viene anche detto semplicemente complemento. • Regola pratica: il complemento a uno di un numero binario A si ottiene cambiando il valore di tutti i suoi bit (complementando ogni bit) Esempio: A = 1011 ® A = 0100 © Piero Demichelis 43

Complemento a 2 • Considerando numeri binari di n bit, si definisce complemento a due di un numero A la quantità: A = 2 n – A Regola pratica: il complemento a due di un numero binario A si ottiene sommando uno al suo complemento (a uno) Esempio: A = 1011 ® A = 0100 ® A = 0101 © Piero Demichelis 44

Complemento a 2 • E’ usato per rappresentare numeri relativi: ( A ³ 0 ) ( A < 0 ) 0 A 2 (= AMS) complemento a 2 di A • In questo modo l’MSB indica il segno: 0 = +, 1 = • Regola alternativa per la determimazione del complemento a due: si parte da destra, si lasciano inalterati tutti gli zeri fino al primo uno che si lascia inalterato, si complementano tutti gli altri bit • Esempio: A = 001101001000; A = 110010111000 © Piero Demichelis 45

Complemento a 2 • Esempio usando una codifica su 4 bit: + 310 0 ( 32 ) 310 0011 CA 2 1100 + 1 1101 CA 2 • In generale su N bit sono rappresentabili i valori: ( 2 N 1 ) x + ( 2 N 1 1 ) 8 bit 16 bit => [ 128 ÷ +127 ] [ 32. 768 ÷ +32. 767 ] © Piero Demichelis 46

Somma e sottrazione in complemento a 2 • La somma si effettua direttamente, senza badare ai segni degli operandi, come fossero due normali numeri binari. • La sottrazione si effettua sommando al minuendo il complemento a 2 del sottraendo: A – B ® A + ( B) ovvero: A + B • Esempio: 0 1 0 + 1 0 1 0 0 = 12 = 1 1 0 2 © Piero Demichelis 47

Overflow • Si usa il termine overflow per indicare l’errore che si verifica in un sistema di calcolo automatico quando il risultato di un’operazione non è rappresentabile con la medesima codifica e numero di bit degli operandi. • Nella somma in binario puro si ha overflow quando si opera con un numero fisso di bit e si genera un riporto (carry) sul bit più significativo (MSB, quello più a sinistra). Esempio: somma tra numeri di 4 bit in binario puro 0 1 + 1 1 1 0 = overflow! ® 1 0 0 1 1 © Piero Demichelis 48

Overflow in complemento a 2 1. Operandi con segno discorde: non si può mai verificare overflow!!!!! 2. Operandi con segno concorde: c’è overflow quando il risultato ha segno discorde da quello dei due operandi 3. In ogni caso, si trascura sempre il carry (riporto) oltre il MSB Esempi: 0 1 + 0 1 0 0 = 1 0 0 1 overflow! 1 1 1 0 + 1 1 0 1 = 1 1 0 1 1 = carry, risultato OK © Piero Demichelis 49

Fixed-point • Si usa un numero fisso di bit per la parte intera e per quella frazionaria (e non si rappresenta la virgola!) • Ad esempio (4 + 4 bit, binario puro): 15. 9375 = 1111 0. 0625 = 00000001 virgola sottintesa © Piero Demichelis 50

Fixed-point • Vantaggi: gli operandi sono allineati per cui le operazioni aritmetiche risultano facili ed immediate; la precisione assoluta è fissa • Svantaggi: l’intervallo di valori rappresentati è assai modesto la precisione dei numeri frazionari rappresentati molto scarsa • Utilizzo tipico: DSP (Digital Signal Processor) Sistemi digitali per applicazioni specifiche (special-purpose) Numeri interi nei calcolatori © Piero Demichelis 51

Rappresentazione di numeri interi • A causa dell’estrema semplicità che presentano le operazioni aritmetiche in complemento a 2, in tutte le macchine numeriche i numeri interi vengono rappresentati in questo codice. • Il numero di bit utilizzati dipende dalla macchina: si tratta generalmente di 16 bit (interi corti) o 32 bit (interi lunghi). • La rappresentazione è nota col nome di fixed-point e il punto frazionario è supposto all’estrema destra della sequenza di bit (parte frazionaria nulla). © Piero Demichelis 52

Rappresentazione di numeri reali • Le rappresentazioni fin qui considerate hanno il pregio di rappresentare esattamente i numeri (almeno quelli interi) ma richiedono un numero di bit esorbitante quando il numero da rappresentare ha valore elevato. • La rappresentazione dei numeri frazionari che deriva dai codici precedenti, ovvero in fixed point, a causa delle forti approssimazioni che impone è usata raramente. • Generalmente viene utilizzato un apposito codice noto come floating point che consente di rappresentare in un numero limitato di bit grandezze di qualsiasi valore anche se condizionate da approssimazioni più o meno elevate. © Piero Demichelis 53

Rappresentazione di numeri in floating point Realizza un compromesso tra l'intervallo dei valori rappresentati e la precisione della rappresentazione. Utilizza una notazione del tipo mantissa + esponente dove il numero di bit dedicati • alla mantissa influisce sulla precisione • all' esponente influisce sull' ampiezza dell'inter-vallo di valori rappresentabili Elementi di Informatica - Aritmetica del calcolatore 54 ã A. Valenzano - 1996 -2

La notazione scientifica • Numeri in virgola fissa su 6 cifre decimali. Intervallo esprimibile: 0 999999 ( 106) • Numeri in notazione scientifica su 6 cifre. Forma: X. YYY 10 WW • Dove la parte intera X esprime la quantità, il numero di cifre della parte frazionaria YYY la precisione, l’esponente WW l’ordine di grandezza. Elementi di Informatica - Aritmetica del calcolatore 55 55 ã A. Valenzano - 1996 -2

La notazione scientifica (2) • Intervallo di valori espressi: 0 (0. 000 100) 10100 (9. 999 1099) • Con 6 cifre, si rappresentano sempre 106 numeri differenti, ma – Nella rappresentazione in virgola fissa, sono equispaziati – Nella rappresentazione in virgola mobile, non sono distribuiti uniformemente: vicino allo zero, i numeri differiscono di 10 -3; vicino al valore massimo, differiscono di 10 -3 1099= 1096. Elementi di Informatica - Aritmetica del calcolatore 56 56 ã A. Valenzano - 1996 -2

Standard IEEE P 754 Definisce i formati per la rappresentazione dei numeri in virgola mobile ma anche: • le conversioni tra formati floating point differenti; • le conversioni tra numeri f. p. ed interi o numeri rappresentati in codice BCD; • • i risultati delle operazioni aritmetiche; i metodi di trattamento di situazioni di eccezione (es. divisione per zero, errori di overflow, under-flow etc. ). Elementi di Informatica - Aritmetica del calcolatore 57 ã A. Valenzano - 1996 -2

Single basic format P 754 (32 bit) I numeri sono normalizzata: pensati nella forma X = (-1)s(1. m)2 e dove: • s è il bit di segno; • e è l'esponente rappresentato in codice eccesso 127 (cioè esponente vero + 127) su 8 bit ( -126 e 127); Elementi di Informatica - Aritmetica del calcolatore 58 ã A. Valenzano - 1996 -2

Single basic format P 754 (32 bit) • m è la mantissa rappresentata in forma normalizzata su 23 bit in modo che il primo bit abbia peso 2 -1; (il bit 20 sempre uguale a 1 non viene rappresentato ed è detto hidden bit) Esempio: 13. 2510 va trasformato nella forma normalizzata: +1101. 012 = +1. 101012 23 Elementi di Informatica - Aritmetica del calcolatore 59 ã A. Valenzano - 1996 -2

Struttura della rappresentazione single basic format s e m Esempio: rappresentare 11. 7510 in P 754 s. b. f. 11. 7510 = 1011. 112 = 1. 01111*23 Þ s =0 e = 10000010 m = 01111. . 0 10000010 01111000000000 Elementi di Informatica - Aritmetica del calcolatore 60 ã A. Valenzano - 1996 -2

Caratteristiche della rappresentazione P 754 su 32 bit Range della rappresentazione: si considerano i valori assoluti dei numeri normalizzati rappresentabili: Nmax = 1. 111. . . · 2127 = 3. 4 · 1038 Elementi di Informatica - Aritmetica del calcolatore 61 ã A. Valenzano - 1996 -2

Distribuzione dei numeri in f. p. 0 1. 0. . * 2 -8 -4 -2 -1 1 2 1 1. 0. . * 2 4 23 2 numeri Elementi di Informatica - Aritmetica del calcolatore 62 2 3 8 23 2 numeri 62 ã A. Valenzano - 1996 -2

Interpretazione di un numero f. p. Sia s il bit del segno, e l’esponente, f la parte frazionaria. • Se e = 0 ed f = 0, il valore è (-1)s 0, cioè +0 oppure -0 • Se e = 0 ed f 0, è una forma denormalizzata (esempio: si possono rappresentare gli interi su 23 bit, ecc. ) Elementi di Informatica - Aritmetica del calcolatore 63 63 ã A. Valenzano - 1996 -2

Interpretazione di un numero f. p. (2) • Se 0 < e < 255, è una forma normalizzata e il valore è (-1)s (1. f) 2(e-127) • Se e = 255 ed f 0, si rappresenta (-1)s( ) cioè un numero infinitamente grande o infinitamente piccolo Elementi di Informatica - Aritmetica del calcolatore 64 64 ã A. Valenzano - 1996 -2

Interpretazione di un numero f. p. (3) • Se e = 255 ed f = 0, non si tratta di un numero valido (not a number, NAN): permette di codificare condizioni particolari, quali operazione non valida, overflow, ecc. Elementi di Informatica - Aritmetica del calcolatore 65 65 ã A. Valenzano - 1996 -2

Operazioni in f. p. Gli operandi sono da riportare nella forma: 1. xxxxx…x 2 a 1. yyyyy…y 2 b dove a e b sono gli esponenti eccesso 127 SOMMA – SOTTRAZIONE Si eseguono le operazioni con gli algoritmi del modulo e segno. Elementi di Informatica - Aritmetica del calcolatore 66 66 ã A. Valenzano - 1996 -2

Operazioni in f. p. (2) Si devono allineare i numeri rispetto al punto decimale, riportandoli allo stesso esponente. Si fa scorrere a destra il valore minore (in modulo) di un numero di posizioni pari alla differenza degli esponenti. La differenza degli esponenti si può fare direttamente sui valori eccesso 127: (a’+127)-(b’+127) = a’-b’. L’esponente del risultato è quello del modulo maggiore. Potrebbe essere richiesta una ri 67 Elementi di Informatica - Aritmetica del calcolatore 67 ã A. Valenzano - 1996 -2 normalizzazione del risultato.

Operazioni in f. p. (3) PRODOTTO Si sommano gli esponenti normalizzati e si sottrae 127: (a’+127) + (b’+127) = (a’+b’+127)+127. Si moltiplicano le mantisse di 24 bit, ottenendo il prodotto su 48 bit: il risultato deve essere troncato ai 24 bit più significativi (precisione di 223). Può essere richiesta una rinormalizzazione: 1. x… 1. y… < 1002 68 = 4 Elementi di Informatica - Aritmetica del calcolatore 68 ã A. Valenzano - 1996 -2

Operazioni in f. p. (4) DIVISIONE Si sottraggono gli esponenti normalizzati e si somma 127: (a’+127) - (b’+127) = (a’-b’). Il dividendo, di 24 bit, si estende a 48 bit, inserendo zeri a destra, e si divide per il divisore, di 24 bit: il risultato, di 24 bit, ha la precisione di 2 -23. Può essere richiesta una rinormalizzazione. Elementi di Informatica - Aritmetica del calcolatore 69 69 ã A. Valenzano - 1996 -2

Osservazioni sul f. p. I risultati delle operazioni in f. p. possono dipendere dall’ordine di esecuzione. Esempio 1016 + 2 - 1016 e 1016 - 1016 + 2 danno risultati diversi. Elementi di Informatica - Aritmetica del calcolatore 70 70 ã A. Valenzano - 1996 -2

Osservazioni sul f. p. (2) In generale, in f. p. vale a+b=a se a / b > 224 16 106 Esempio: non ha senso incrementare di uno un valore positivo a se a è molto maggiore di 1. Elementi di Informatica - Aritmetica del calcolatore 71 71 ã A. Valenzano - 1996 -2

Floating-point • E’ basata sul formato esponenziale (notazione scientifica) N = mantissa base esponente Ricorda le notazioni: standard 3. 5 × 104 scientifico 0. 35 × 105 3. 5 E+4 0. 35 E+5 • Nei sistemi di elaborazione Base = 2 Mantissa ed esponente sono rappresentati in binario © Piero Demichelis 72

Floating-point • Vantaggi: grande intervallo di valori rappresentabili errore relativo fisso • Svantaggi: operandi non allineati per cui le operazioni aritmetiche risultano molto complesse errore assoluto variabile e dipendente dal valore del numero • E’ la rappresentazione utilizzata da tutti i calcolatori elettronici per rappresentare i numeri frazionari ed è stata standardizzata dall’IEEE. © Piero Demichelis 73

Formato IEEE-P 754 • Standard IEEE per il floating point: Rappresentazione binaria di mantissa esponente segno • Singola precisione: 32 bit (float) segno 1 bit esponente 8 bit mantissa precisione: circa 7 cifre decimali 23 bit • Doppia precisione: 64 bit (double) segno esponente mantissa 1 bit 11 bit 52 bit precisione: circa 17 cifre decimali © Piero Demichelis 74

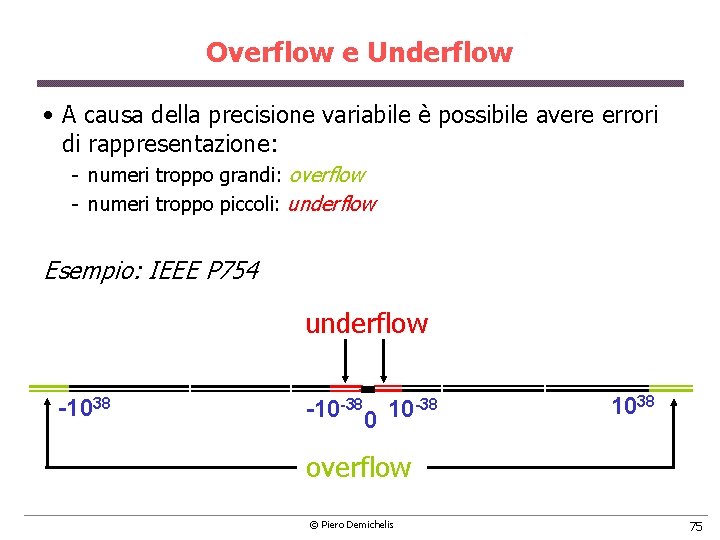
Overflow e Underflow • A causa della precisione variabile è possibile avere errori di rappresentazione: numeri troppo grandi: overflow numeri troppo piccoli: underflow Esempio: IEEE P 754 underflow -1038 -10 -38 0 10 -38 1038 overflow © Piero Demichelis 75

Rappresentazioni di dati non numerici • Qualunque insieme finito di oggetti può essere codificato tramite valori numerici associando ad ogni oggetto un codice (ad esempio un numero intero). • Nel sistema numerico binario per rappresentare K oggetti distinti occorre un numero minimo di bit pari a: N = é log 2 K ù © Piero Demichelis 76

Caratteri • E’ sicuramente il tipo di informazione più scambiata: occorre pertanto una codifica standard. la più usata fa riferimento al codice ASCII (American Standard Code for Information Interchange) in passato era molto diffuso il codice EBCDIC (Extended BCD Interchange Code) codice UNICODE © Piero Demichelis 77

Codice ASCII • E’ usato anche nelle telecomunicazioni. • Usa 8 bit per rappresentare: i 52 caratteri alfabetici (a ÷ z , A ÷ Z) le 10 cifre (0 ÷ 9) i segni di interpunzione (, ; : !? &%=+-/ ecc. ) un gruppo di caratteri di controllo tra cui: CR LF, NL FF, NP HT VT NUL BEL EOT ( ( ( ( 13 ) 10 ) 12 ) 9 ) 11 ) 0 ) 7 ) 4 ) Carriage Return New Line, Line Feed New Page, Form Feed Horizontal Tab Vertical Tab Null Bell End-Of-Transmission © Piero Demichelis 78

Codice ASCII • Ad esempio per rappresentare il messaggio “Auguri a tutti!” è necessaria la seguente sequenza: 01000001 01110101 011001110101 01110010 01101001 00100000 01100001 A u g u r i spazio a 00100000 01110101 01110100 01101001 00100001 © Piero Demichelis spazio t u t t i ! 79

Fine Rappresentazione dei dati