TEORIA DEGLI INSIEMI INIZIO N 2 LE OPERAZIONI

























- Slides: 30

TEORIA DEGLI INSIEMI INIZIO

N° 2 LE OPERAZIONI FONDAMENTALI CON GLI INSIEMI N° 1 GLI INSIEMI N° 3 LE RELAZIONI TRA INSIEMI

N° 1 GLI INSIEMI M. Escher

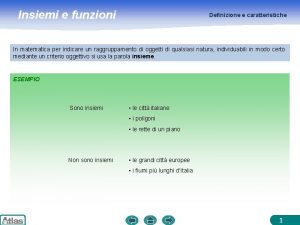
Il concetto di insieme Nel linguaggio comune il termine insieme indica un raggruppamento, una raccolta, una collezione di elementi che possono essere oggetti, individui, simboli, numeri, figure geometriche… Un insieme si può considerare definito solo se è possibile decidere inequivocabilmente se un elemento appartiene o no all’insieme.

Esempi: “Gli alunni simpatici di questa classe” non costituiscono un insieme, perché non si conosce un criterio oggettivo in base al quale un alunno è considerato simpatico, ma esistono soltanto criteri soggettivi. Invece “gli alunni di questa classe più alti di 1, 70 m” costituiscono un insieme; infatti posso stabilire, misurando la loro altezza, quali alunni appartengono al suddetto insieme e quali no; quindi ho un criterio oggettivo.

Il simbolo di appartenenza Generalmente gli insiemi si indicano con lettere maiuscole: A, B, C, …, X, Y, … Gli elementi di un insieme con lettere minuscole: a, b, c, …, x, y, … Per indicare che un elemento “a” appartiene ad un insieme A si usa il simbolo di appartenenza ; la scrittura a A si legge “a appartiene ad A”. Per indicare invece che un elemento x non è dell’insieme A, si scrive x A, e si legge “x non appartiene ad A”.

Rappresentazioni di un insieme Un insieme può essere rappresentato in 3 modi diversi: Con i diagrammi di Eulero-Venn; In modo estensivo; In modo intensivo.

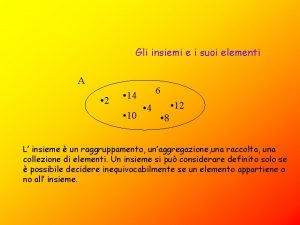
Con i diagrammi di Eulero-Venn si dà una rappresentazione geometrica: gli elementi all’interno della linea appartengono all’insieme A, quelli all’esterno no. A f b a g c d e

La rappresentazione estensiva o tabulare consiste nell’elencare i nomi degli elementi dell’insieme scrivendoli tra parentesi graffe, senza ripetizioni e senza dare importanza all’ordine. Esempio Consideriamo l’insieme C delle consonanti della parola “stivale”; la sua rappresentazione estensiva è: C= s, t, v, l

Infine, la rappresentazione intensiva di un insieme è la specificazione di una proprietà p(x), se esiste, che ne caratterizza gli elementi. Esempio L’insieme A dei numeri naturali minori di 5 può essere così rappresentato: A= x N / x < 5

Insiemi uguali, insieme vuoto DEF Diremo uguali due insiemi A e B quando hanno esattamente gli stessi elementi, ossia quando ogni elemento di A appartiene a B e quando ogni elemento di B appartiene ad A. Per indicare che due insiemi A e B sono uguali scriveremo A=B. E’ questo il cosiddetto: principio di equiestensione

Esempio Sia C l’insieme delle consonanti della parola “stivale” e D quello delle consonanti della parola “velista”; rappresentiamoli: C= s, t, v, l D= v, l, s, t Poiché i due insiemi contengono gli stessi elementi, per il principio di equiestensione, essi sono uguali: C=D

Consideriamo ora l’insieme dei cerchi con 3 angoli. L’insieme è ben definito, ossia esiste un criterio oggettivo per stabilire se un elemento appartiene o no a questo insieme, eppure ci rendiamo conto che non esiste alcun elemento che soddisfi la proprietà enunciata perché non esistono cerchi che abbiano degli angoli; allora: DEF Definiamo insieme vuoto l’insieme che non ha alcun elemento. Tale insieme lo indicheremo con il simbolo: oppure

Insieme ambiente o universo Quando si rappresenta un insieme mediante la proprietà caratteristica, occorre indicare l’ambiente da cui trarre gli elementi x dell’insieme. Questo ambiente, cioè la totalità degli elementi, è esso stesso un insieme e viene detto: insieme ambiente o insieme universo.

Sottoinsiemi B A Tutti gli elementi di B appartengono anche a A Es: B={1, 2, 3} A= {1, 2, 3, 4, 5} A 2 1 3 4 5 B

N° 2 LE OPERAZIONI FONDAMENTALI CON GLI INSIEMI

Unione tra 2 insiemi A B E’ l’insieme formato dagli elementi che si trovano in A o in B Es: A = {1, 2, 3} B ={2, 4, 5} A U B = {1, 2, 3, 4, 5} B A 4 1 2 3 5

Intersezione A B E’ l’insieme formato dagli elementi che si trovano sia in A che in B Es: A = {1, 2, 3} B ={2, 4, 5} A B = {2} A 1 4 2 3 5 A B B

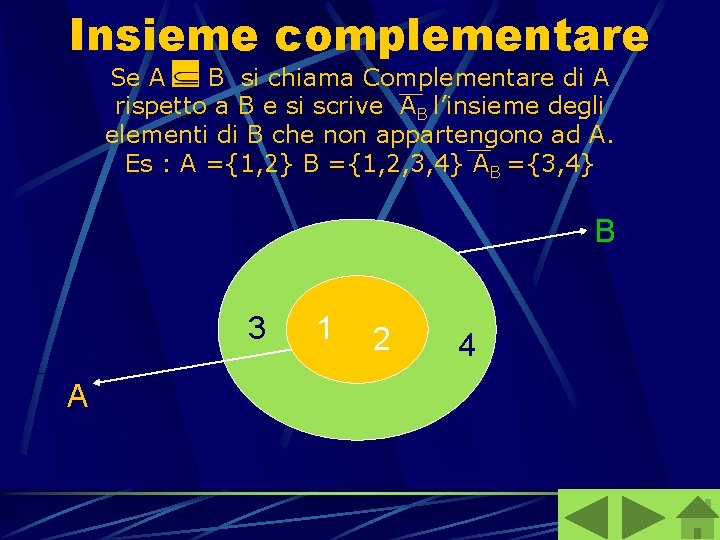
Insieme complementare Se A B si chiama Complementare di A rispetto a B e si scrive AB l’insieme degli elementi di B che non appartengono ad A. Es : A ={1, 2} B ={1, 2, 3, 4} AB ={3, 4} B 3 A 1 2 4

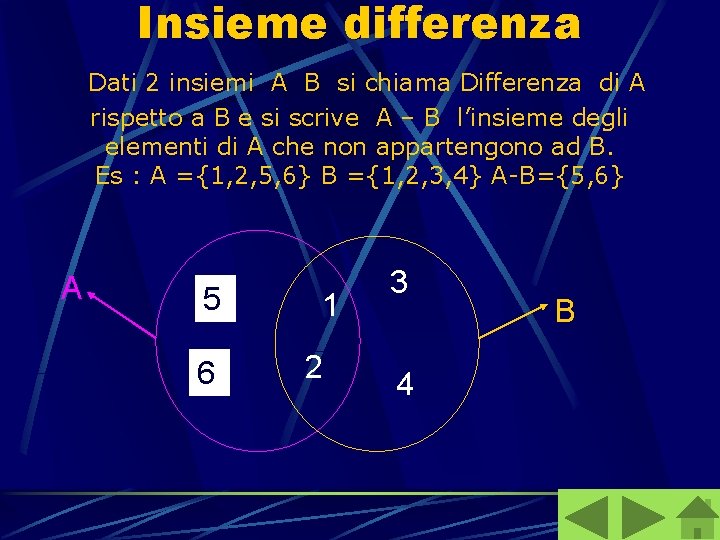
Insieme differenza Dati 2 insiemi A B si chiama Differenza di A rispetto a B e si scrive A – B l’insieme degli elementi di A che non appartengono ad B. Es : A ={1, 2, 5, 6} B ={1, 2, 3, 4} A-B={5, 6} A 5 6 1 2 3 4 B

N° 3 LE RELAZIONI TRA DUE INSIEMI

Concetto di relazione Una relazione tra due insiemi A e B è un insieme di coppie formate ognuna da un elemento di A, e da uno di B; i due elementi si dicono allora in relazione. Il primo insieme si dice dominio della relazione, il secondo codominio. A B

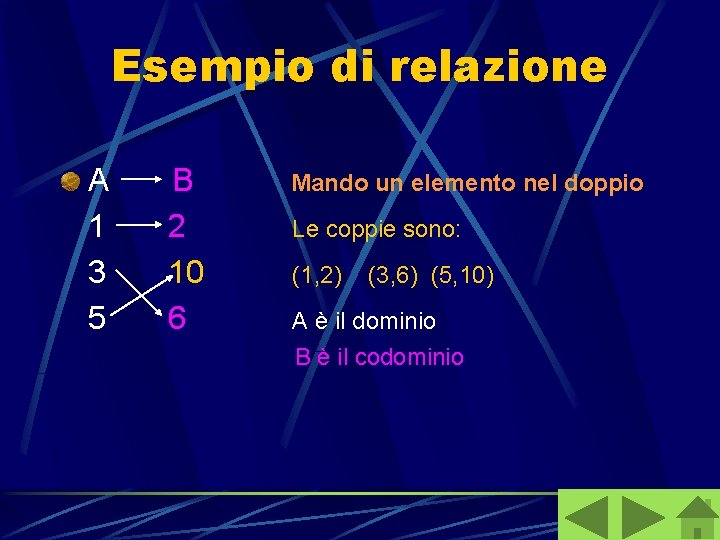
Esempio di relazione A 1 3 5 B 2 10 6 Mando un elemento nel doppio Le coppie sono: (1, 2) (3, 6) (5, 10) A è il dominio B è il codominio

Immagine Data una relazione tra A e B si chiama immagine di un elemento a A l’insieme degli elementi in relazione con a e si indica con f(a) dove f indica la relazione A 8 6 9 7 B 2 4 3 5 Mando un elemento di A in un in suo divisore in B f(8)={2, 4} f(6)={2, 3} f(9)={3} f(7)=Φ L’immagine di tutta la relazione è {2, 4, 3}

Controimmagine Data una relazione tra A e B si chiama controimmagine di un elemento b B l’insieme degli elementi in relazione con b e si indica con f-1(b) dove f indica la relazione A 8 6 9 7 B 2 4 3 5 Mando un elemento di A in un in suo divisore in B f-1(2)={8, 6} f-1(4)={8} f-1(3)={6, 9} f-1(5)=Φ La controimmagine di tutta la relazione è {8, 6, 9}

Funzione Data una relazione tra A e B si dice che è una funzione se ogni elemento di A ha uno ed un solo corrispondente il B. Es: f: A ------>B g: A------> B h: A------>B 1 a 1 a 2 b 2 b 3 c 3 c La f non è una funzione perché 1 non ha corrispondente, la g non è una funzione perché 2 ha due corrispondenti, la h è una funzione perché ogni elemento di A ha uno ed un solo corrispondente. Il controllo si fa sull’insieme A!

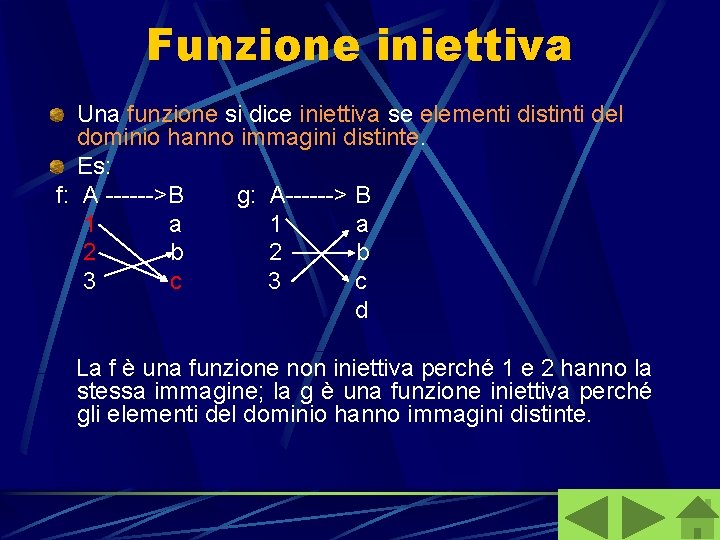
Funzione iniettiva Una funzione si dice iniettiva se elementi distinti del dominio hanno immagini distinte. Es: f: A ------>B g: A------> B 1 a 2 b 3 c d La f è una funzione non iniettiva perché 1 e 2 hanno la stessa immagine; la g è una funzione iniettiva perché gli elementi del dominio hanno immagini distinte.

Funzione suriettiva Una funzione si dice suriettiva se ogni elemento del codominio ha una controimmagine. Es: f: A ------>B g: A------> B 1 a 2 b 3 c 3 La f è una funzione non suriettiva perché c no ha una controimmagine; la g è una funzione suriettiva perché tutti gli elementi del codominio hanno una controimmagine.

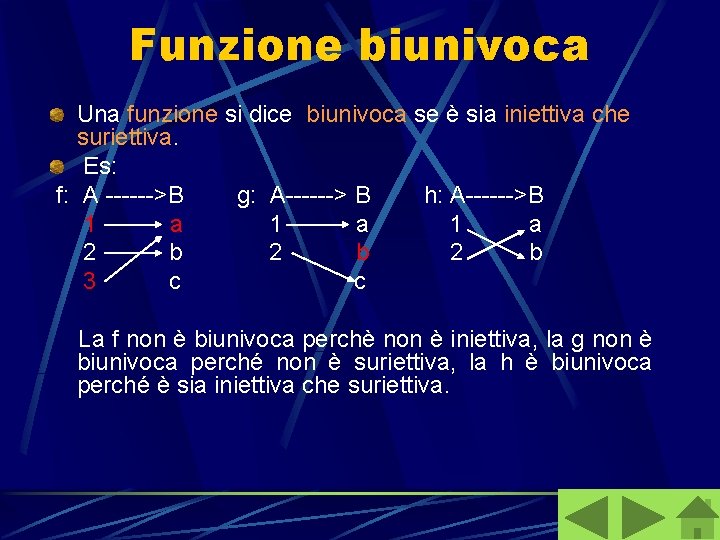
Funzione biunivoca Una funzione si dice biunivoca se è sia iniettiva che suriettiva. Es: f: A ------>B g: A------> B h: A------>B 1 a 1 a 2 b 2 b 3 c c La f non è biunivoca perchè non è iniettiva, la g non è biunivoca perché non è suriettiva, la h è biunivoca perché è sia iniettiva che suriettiva.

Funzione inversa Una funzione biunivoca ha una funzione inversa che si ottiene scambiando dominio e codominio e prendendo le coppie in ordine inverso. Se la funzione si indica con f la sua inversa si indica con f-1 Es: f: A 1 2 3 B a b c f-1 : B A a b c 1 2 3
 Sintomi menopausa nausea
Sintomi menopausa nausea Decameron data
Decameron data Esami in gravidanza tabella
Esami in gravidanza tabella Posizionamento arbitro
Posizionamento arbitro Umanesimo e rinascimento
Umanesimo e rinascimento Quel ramo del lago di como analisi
Quel ramo del lago di como analisi Sintomi della premenopausa
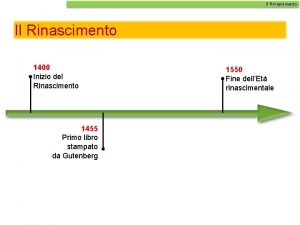
Sintomi della premenopausa Inizio rinascimento
Inizio rinascimento Caratteristiche della lettera
Caratteristiche della lettera Stakeholder secondari
Stakeholder secondari Teoria degli algoritmi
Teoria degli algoritmi Termometro clinico portata e sensibilità
Termometro clinico portata e sensibilità Propagazione errore massimo
Propagazione errore massimo Strumento analogico esempio
Strumento analogico esempio Unione tra due insiemi
Unione tra due insiemi Prodotto cartesiano a x b x c
Prodotto cartesiano a x b x c Soluzione al paradosso di russell
Soluzione al paradosso di russell Simbolo circa
Simbolo circa Insiemi disgiunti
Insiemi disgiunti Insiemi simbologia
Insiemi simbologia Linguaggio insiemi
Linguaggio insiemi Insieme vuoto
Insieme vuoto Insiemi con frazioni
Insiemi con frazioni Espressioni con numeri negativi
Espressioni con numeri negativi Espressioni polinomi esercizi
Espressioni polinomi esercizi Proprietà distributiva
Proprietà distributiva Schema polinomi
Schema polinomi Somma tra notazioni scientifiche
Somma tra notazioni scientifiche Strisciamento
Strisciamento Operazioni triangolari extra ue
Operazioni triangolari extra ue Come si scrive 324 decimi
Come si scrive 324 decimi