GLI INSIEMI Dispensa a cura del prof Vincenzo

GLI INSIEMI Dispensa a cura del prof. Vincenzo Lo Presti

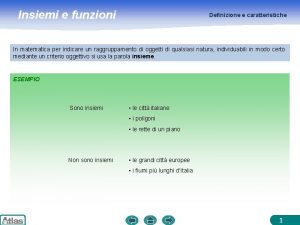
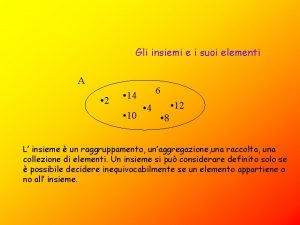
CONCETTO DI INSIEME In matematica si chiama insieme un raggruppamento di cose, persone o entità che rispettano un determinato criterio, mediante il quale si può stabilire con assoluta certezza quali sono gli elementi che compongono l’insieme. RAGGRUPPAMENTI CHE COSTITUISCONO INSIEMI Le città italiane con più di 500. 000 abitanti Gli alunni della classe che pesano sino a 60 kg I rettangoli che hanno la base di 10 cm RAGGRUPPAMENTI CHE NON COSTITUISCONO INSIEMI Le città italiane grandi Gli alunni simpatici della classe I rettangoli piccoli

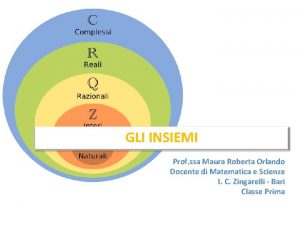
SIMBOLOGIA DEGLI INSIEMI Gli insiemi si indicano con le lettere maiuscole dell’alfabeto italiano: A , B, C, D, E, ……… Gli elementi di un insieme si indicano con le lettere minuscole dell’alfabeto italiano: a, b, c, d, e, ……… In matematica alcune lettere maiuscole sono riservate a particolari insiemi numerici: N Insieme dei numeri naturali P Insieme dei numeri naturali pari D Insieme dei numeri naturali dispari Z Insieme dei numeri interi relativi Q Insieme dei numeri razionali

SIMBOLOGIA DEGLI INSIEMI Nello studio degli insiemi si utilizzano particolari simboli �Simbolo di appartenenza c �B L’elemento c appartiene all’insieme B 4 �N Il 4 appartiene all’insieme dei numeri naturali �Simbolo di non appartenenza -3 �N Il -3 non appartiene all’insieme dei numeri Naturali

TIPI DI INSIEMI Gli insiemi possono essere: Finiti – se hanno un numero ben preciso di elementi Infiniti – se hanno infiniti elementi Esempi: L’insieme dei divisori di 12 è un insieme finito in quanto ha un numero ben preciso di elementi (sei ed esattamente 1, 2, 3, 4, 6, 12) L’insieme dei multipli di 6 è un insieme infinito in quanto ha infiniti elementi (6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72………)

INSIEME VUOTO Un insieme si dice vuoto se non ha elementi L’insieme vuoto si indica con � o con {} Esempi: L’insieme dei multipli di 4 che sono dispari L’insieme dei quadrati con tre lati L’insieme dei divisori di 13 che sono pari

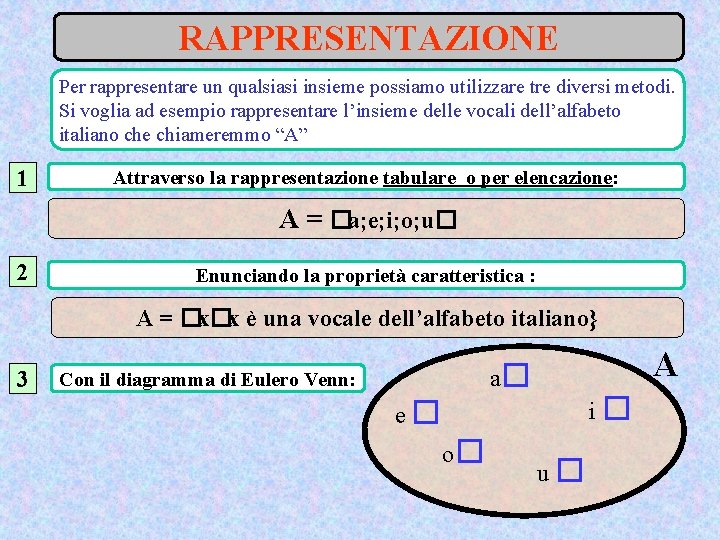
RAPPRESENTAZIONE Per rappresentare un qualsiasi insieme possiamo utilizzare tre diversi metodi. Si voglia ad esempio rappresentare l’insieme delle vocali dell’alfabeto italiano che chiameremmo “A” 1 Attraverso la rappresentazione tabulare o per elencazione: A = �a; e; i; o; u� 2 Enunciando la proprietà caratteristica : A = �x�x è una vocale dell’alfabeto italiano} 3 A a� Con il diagramma di Eulero Venn: i� e� o� u�

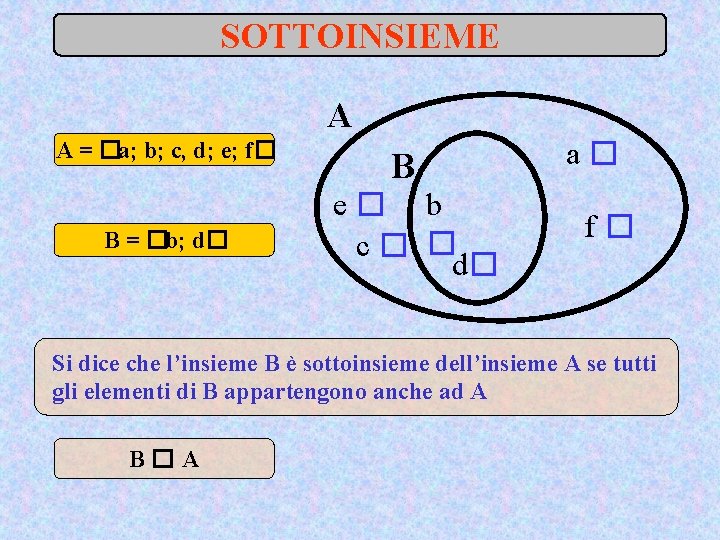
SOTTOINSIEME A A = �a; b; c, d; e; f� B = �b; d� B e� b c� � d� a� f� Si dice che l’insieme B è sottoinsieme dell’insieme A se tutti gli elementi di B appartengono anche ad A B�A

SOTTOINSIEMI, INCLUSIONE “ , ” B è un SOTTOINSIEME IMPROPRIO di A A B C a� b d� �c� B �A Ogni insieme è un SOTTOINSIEME (IMPROPRIO) di sé stesso A �A, B �B, …. . C è un SOTTOINSIEME DI A C�B L’insieme vuoto è un SOTTOINSIEME (IMPROPRIO) di ogni insieme ��C, ��B, …. .

APPARTENENZA e INCLUSIONE APPARTENENZA INCLUSIONE A � L’elemento b appartiene all’insieme A b � d� � � L’insieme �b� è strettamente incluso nell’insieme A �b�� A L’insieme �d; b�è uguale ad A �d; b��A oppure �d; b�= A

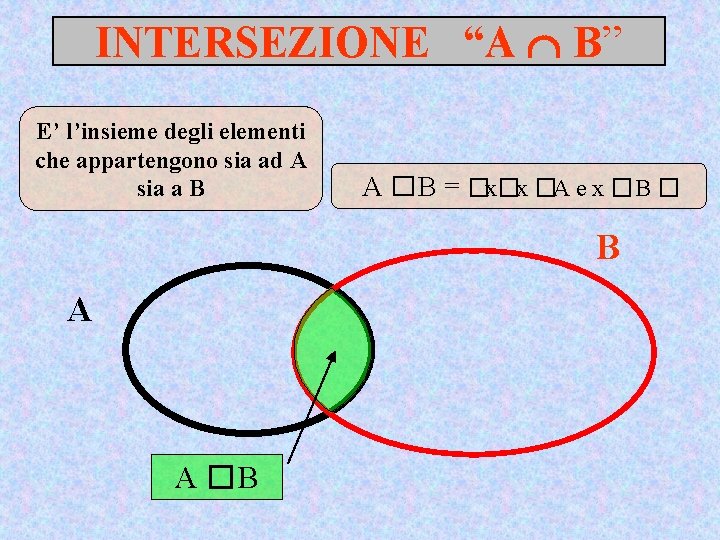
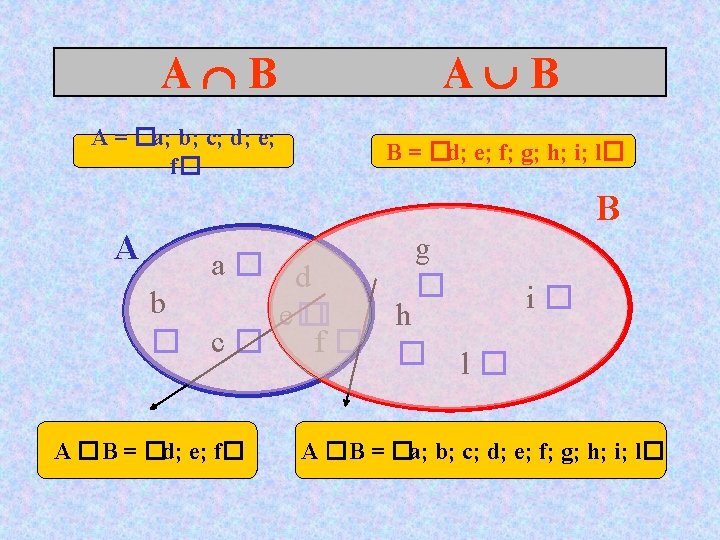
INTERSEZIONE “A B” E’ l’insieme degli elementi che appartengono sia ad A sia a B A �B = �x�x �A e x �B � B A A �B

INSIEMI DISGIUNTI Due insiemi si dicono disgiunti se la loro intersezione è vuota Se A �B = � allora A e B si dicono DISGIUNTI A B

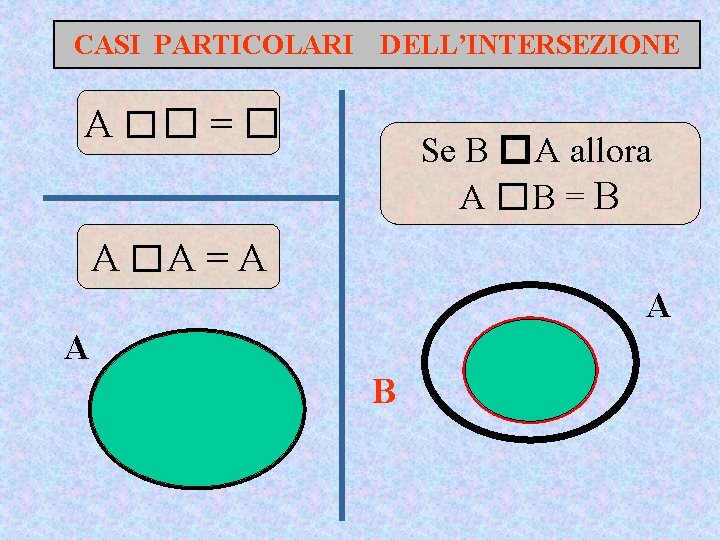
CASI PARTICOLARI DELL’INTERSEZIONE A �� = � Se B �A allora A �B = B A �A = A A A B

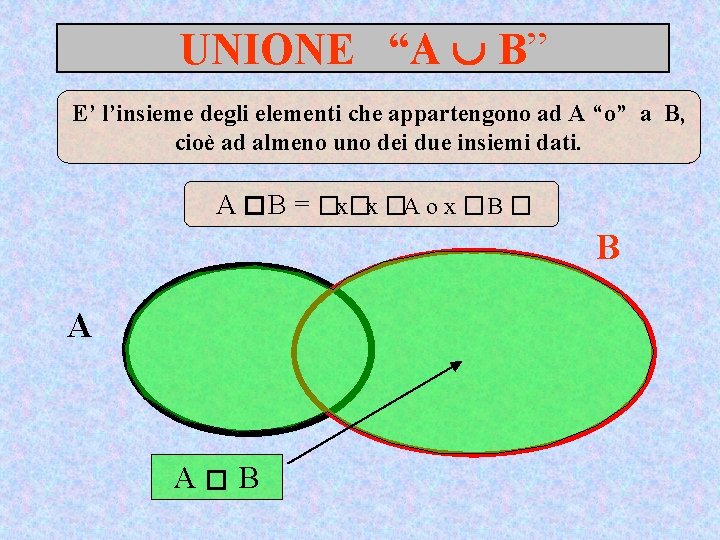
UNIONE “A B” E’ l’insieme degli elementi che appartengono ad A “o” a B, cioè ad almeno uno dei due insiemi dati. A � B = �x�x �A o x �B � B A A� B

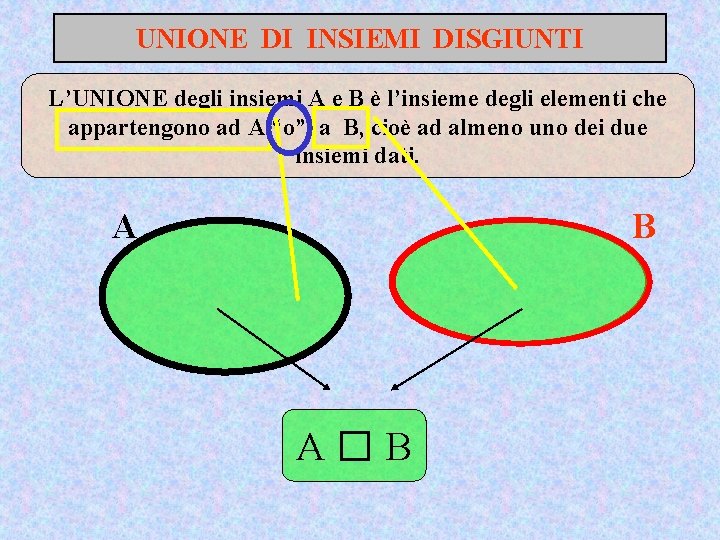
UNIONE DI INSIEMI DISGIUNTI L’UNIONE degli insiemi A e B è l’insieme degli elementi che appartengono ad A “o” a B, cioè ad almeno uno dei due insiemi dati. A B A�B

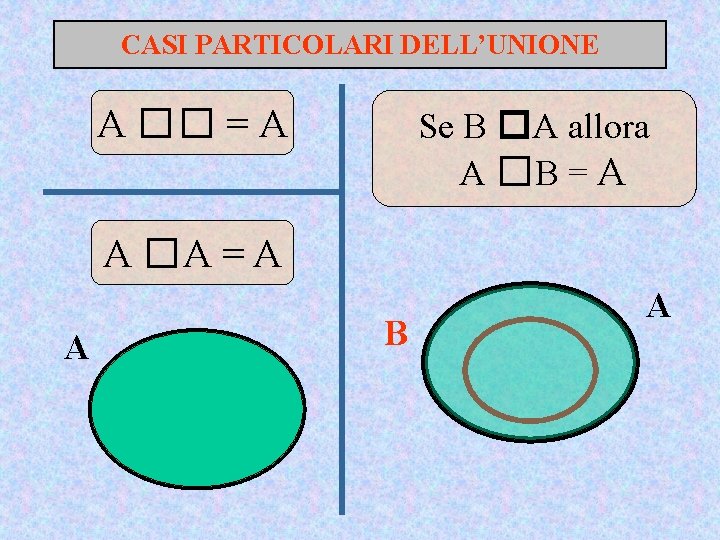
CASI PARTICOLARI DELL’UNIONE A �� = A Se B �A allora A �B = A A �A = A A B A

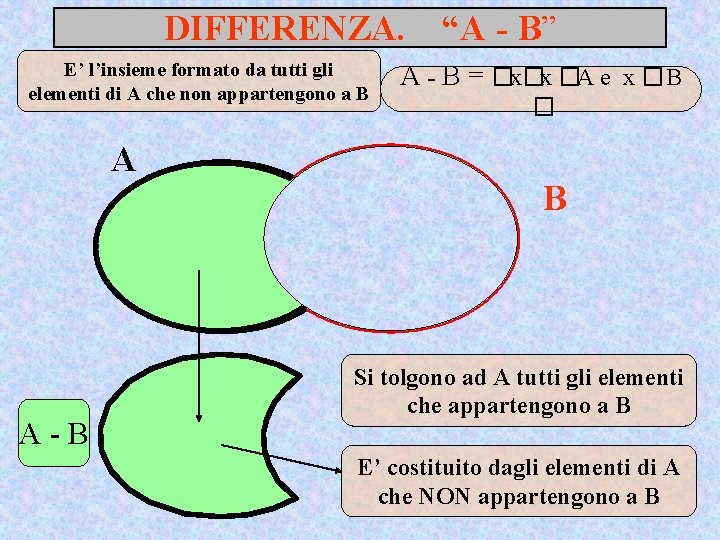
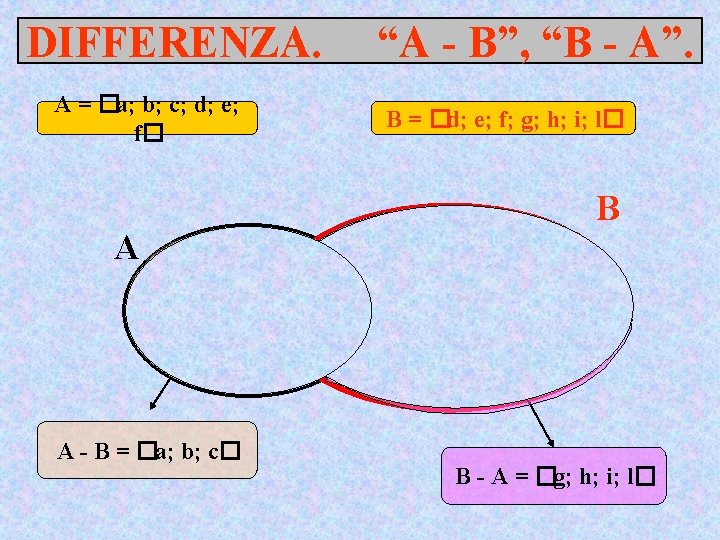
DIFFERENZA. E’ l’insieme formato da tutti gli elementi di A che non appartengono a B A A-B “A - B” A - B = �x�x �A e x �B � B Si tolgono ad A tutti gli elementi che appartengono a B E’ costituito dagli elementi di A che NON appartengono a B

CASI PARTICOLARI DELLA DIFFERENZA TRA INSIEMI A-A=� A-�=A Se A �B = �allora A - B = A e B - A = B Se B �A allora B - A = �

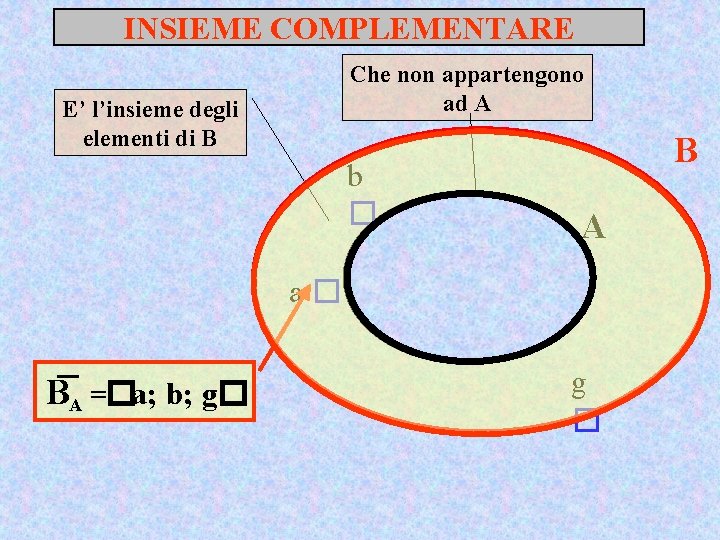
INSIEME COMPLEMENTARE Dati due insiemi A e B con B�A si chiama complementare di B rispetto ad A la differenza A-B BA= A-B = �x�x �A e x �B �

INSIEME COMPLEMENTARE Che non appartengono ad A E’ l’insieme degli elementi di B b � a� BA =�a; b; g� B d A c� � e� f� g �

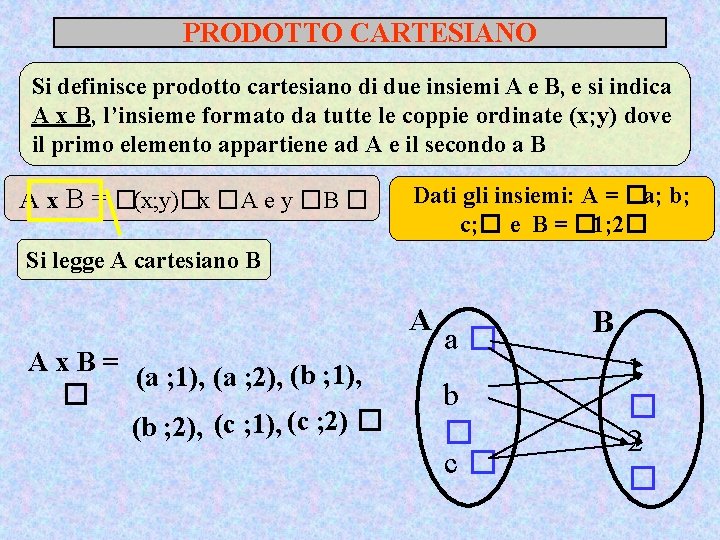
PRODOTTO CARTESIANO Si definisce prodotto cartesiano di due insiemi A e B, e si indica A x B, l’insieme formato da tutte le coppie ordinate (x; y) dove il primo elemento appartiene ad A e il secondo a B A x B = �(x; y)�x �A e y �B � Dati gli insiemi: A = �a; b; c; � e B = � 1; 2� Si legge A cartesiano B A Ax. B= (a ; 1), (a ; 2), (b ; 1), � (b ; 2), (c ; 1), (c ; 2) � a� b � c� B 1 � 2 �

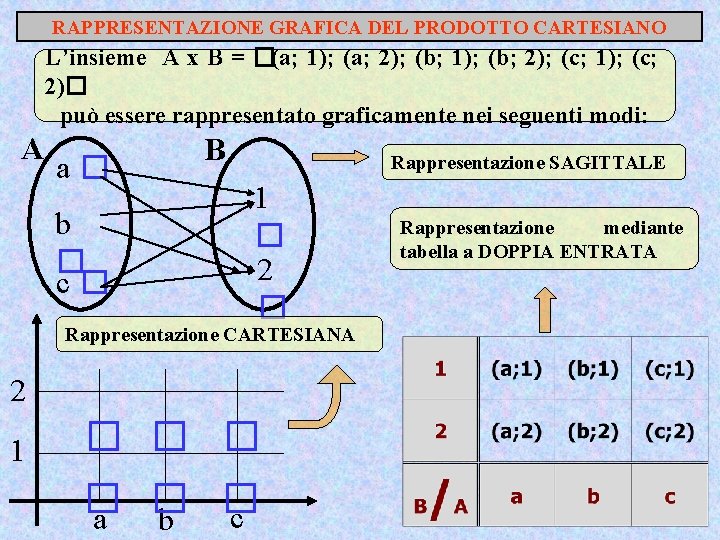
RAPPRESENTAZIONE GRAFICA DEL PRODOTTO CARTESIANO L’insieme A x B = �(a; 1); (a; 2); (b; 1); (b; 2); (c; 1); (c; 2)� può essere rappresentato graficamente nei seguenti modi: A a� b � c� B Rappresentazione SAGITTALE 1 � 2 � Rappresentazione CARTESIANA 2 1 � � � c a b Rappresentazione mediante tabella a DOPPIA ENTRATA

OSSERVAZIONI SUL PRODOTTO CARTESIANO La coppia (x; y) è diversa dalla coppia (y; x) Gli elementi dell’insieme cartesiano sono coppie A x A = A 2 Ax. B �Bx. A Se A e B hanno rispettivamente “n” e “m” elementi, l’insieme A x B possiede “nxm” elementi.

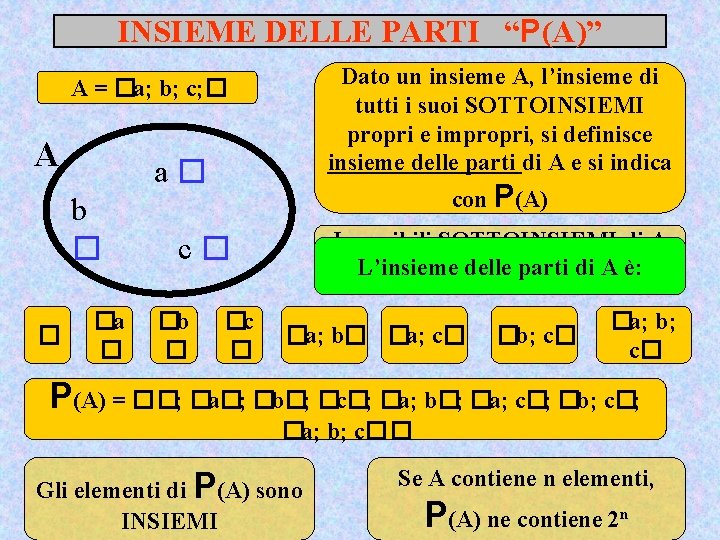
INSIEME DELLE PARTI “P(A)” Dato un insieme A, l’insieme di tutti i suoi SOTTOINSIEMI propri e impropri, si definisce insieme delle parti di A e si indica A = �a; b; c; � A a� b � � �a � con P(A) I possibili SOTTOINSIEMI di A L’insieme delle sono: parti di A è: c� �b � �c � �a; b� �a; c� �b; c� �a; b; c� P(A) = ��; �a�; �b�; �c�; �a; b�; �a; c�; �b; c�; �a; b; c�� Gli elementi di P(A) sono INSIEMI Se A contiene n elementi, P(A) ne contiene 2 n

INSIEME DELLE PARTI “P(A)” Gli elementi di P(A) sono INSIEMI ed esattamente tutti i sottoinsiemi propri e i due sottoinsiemi impropri (l’insieme stesso e l’insieme vuoto) REGOLA PER DETERMINARE IL N. DI ELEMENTI DELL’INSIEME DELLE PARTI Se A contiene n elementi, P(A) ne contiene 2 n Esempi: -Se n=3 (esempio precedente) 23=8 -Se n=5 (esempio precedente) 25=32 -Se n=1 (esempio precedente) 21=2

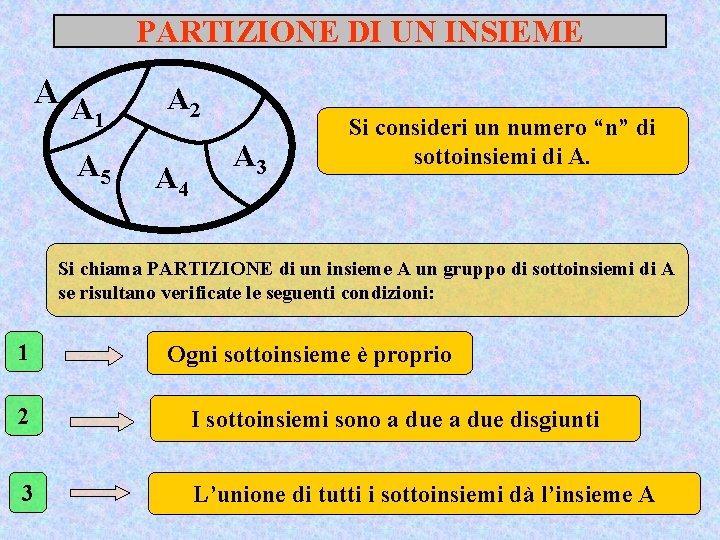
PARTIZIONE DI UN INSIEME AA 1 A 5 A 2 A 4 A 3 Si consideri un numero “n” di sottoinsiemi di A. Si chiama PARTIZIONE di un insieme A un gruppo di sottoinsiemi di A se risultano verificate le seguenti condizioni: 1 Ogni sottoinsieme è proprio 2 I sottoinsiemi sono a due disgiunti 3 L’unione di tutti i sottoinsiemi dà l’insieme A

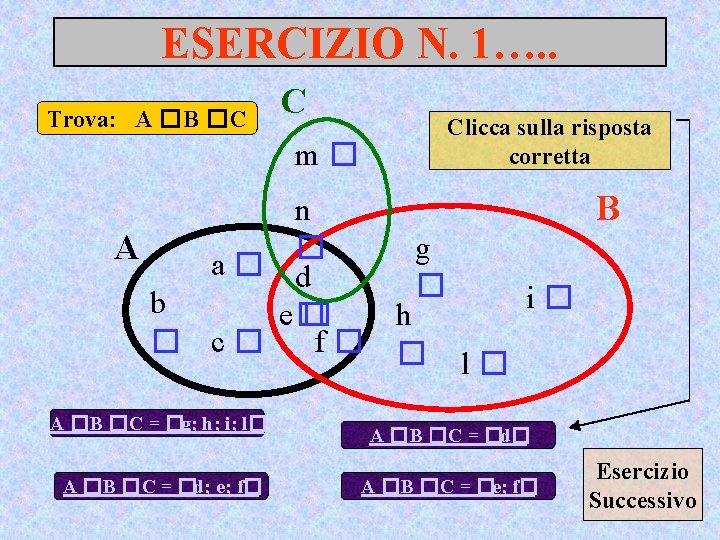
ESERCIZIO N. 1…. . Trova: A �B �C C m� Clicca sulla risposta corretta n B g � A a� d � i� b e� � h f� � � c� l� A �B �C = �g; h; i; l� A �B �C = �d; e; f� A �B �C = �d� A �B �C = �e; f� Esercizio Successivo

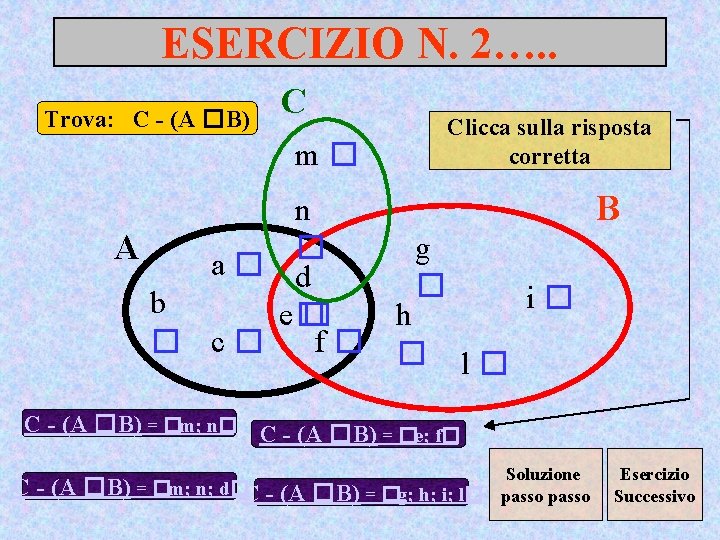
ESERCIZIO N. 2…. . Trova: C - (A �B) C m� Clicca sulla risposta corretta n B g � A a� d � i� b e� � h f� � � c� l� C - (A �B) = �m; n� C - (A �B) = �e; f� C - (A �B) = �m; n; d�C - (A �B) = �g; h; i; l� Soluzione passo Esercizio Successivo

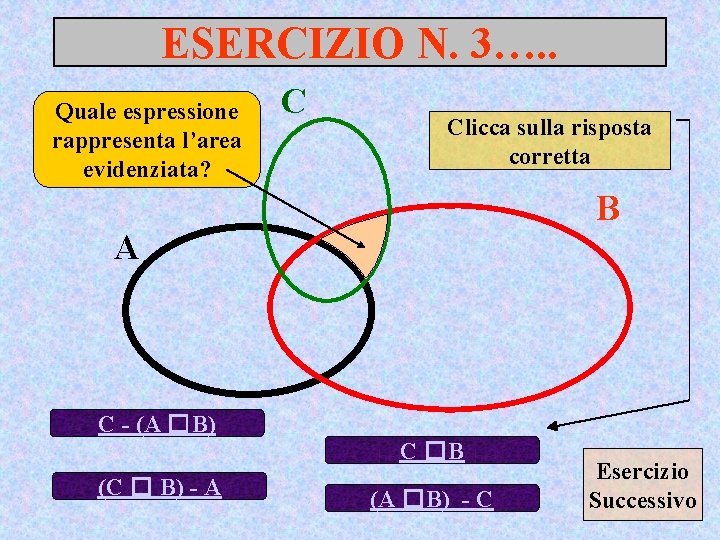
ESERCIZIO N. 3…. . Quale espressione rappresenta l’area evidenziata? C Clicca sulla risposta corretta B A C - (A �B) C �B (C � B) - A (A �B) - C Esercizio Successivo

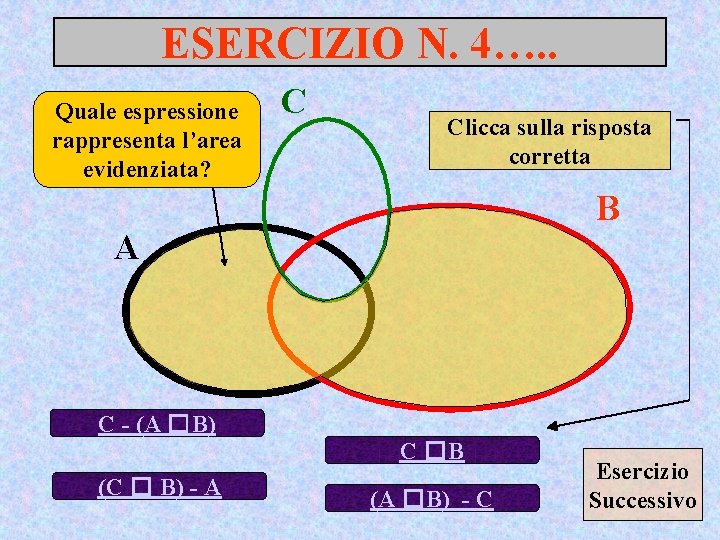
ESERCIZIO N. 4…. . Quale espressione rappresenta l’area evidenziata? C Clicca sulla risposta corretta B A C - (A �B) C �B (C � B) - A (A �B) - C Esercizio Successivo

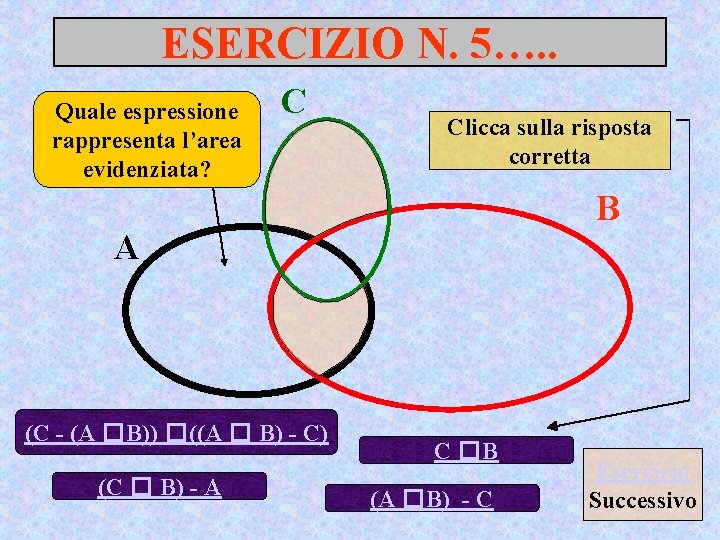
ESERCIZIO N. 5…. . Quale espressione rappresenta l’area evidenziata? C Clicca sulla risposta corretta B A (C - (A �B)) �((A � B) - C) (C � B) - A C �B (A �B) - C Esercizio Successivo

FINE