Insiemi disgiunti 1 Strutture dati per insiemi disgiunti


![Algoritmi per up-tree Si associa ad ogni nodo x un intero rank[x], limite superiore Algoritmi per up-tree Si associa ad ogni nodo x un intero rank[x], limite superiore](https://slidetodoc.com/presentation_image_h/d05b46737db3f79a4ab9ccc7b5af627b/image-9.jpg)




![Up-Tree: complessità Lemma 1 Per tutte le radici x di alberi, size[x] ≥ 2 Up-Tree: complessità Lemma 1 Per tutte le radici x di alberi, size[x] ≥ 2](https://slidetodoc.com/presentation_image_h/d05b46737db3f79a4ab9ccc7b5af627b/image-14.jpg)

- Slides: 15

Insiemi disgiunti 1

Strutture dati per insiemi disgiunti E’ dato un insieme S scomposto in insiemi disgiunti S 1, , Sk. Ogni insieme è identificato da un suo membro rappresentante. Si vogliono realizzare le seguenti operazioni: • Make-Set(x): inizializza un nuovo insieme contenente il solo elemento x • Union(x, y): unisce gli elementi degli insiemi che contengono x e y, S e T rispettivamente, nell’unico insieme S T • Find-Set(x): trova l’insieme a cui appartiene l’elemento x 2

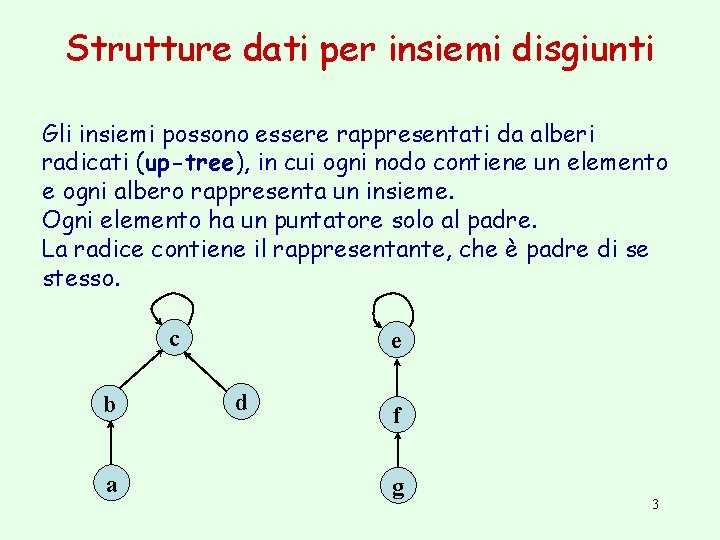
Strutture dati per insiemi disgiunti Gli insiemi possono essere rappresentati da alberi radicati (up-tree), in cui ogni nodo contiene un elemento e ogni albero rappresenta un insieme. Ogni elemento ha un puntatore solo al padre. La radice contiene il rappresentante, che è padre di se stesso. c b a e d f g 3

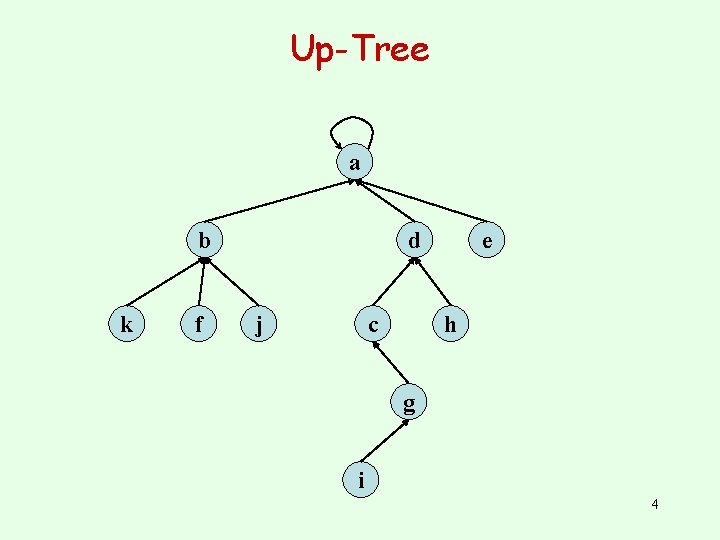
Up-Tree a b k f d j c e h g i 4

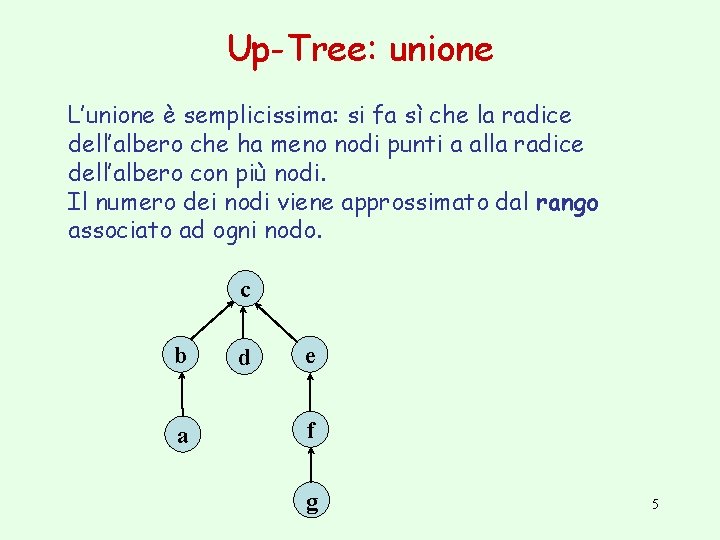
Up-Tree: unione L’unione è semplicissima: si fa sì che la radice dell’albero che ha meno nodi punti a alla radice dell’albero con più nodi. Il numero dei nodi viene approssimato dal rango associato ad ogni nodo. c b a d e f g 5

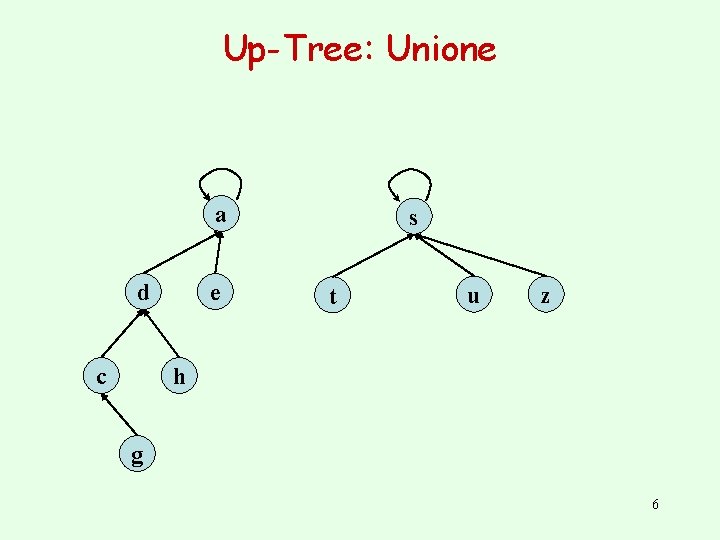
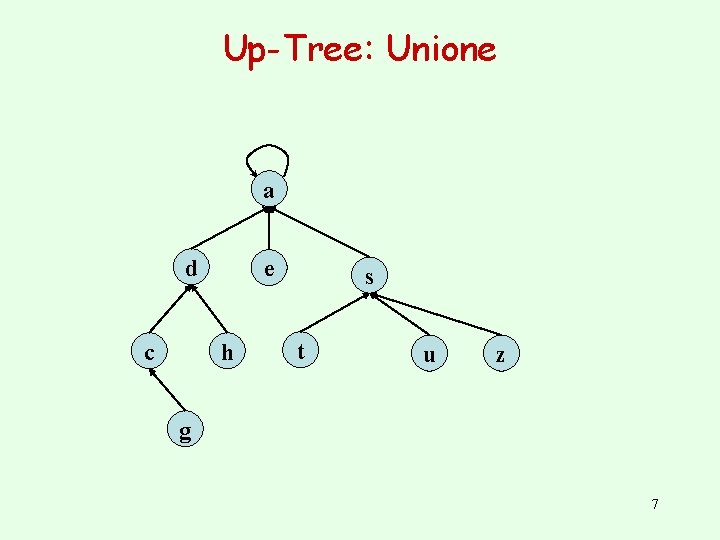
Up-Tree: Unione a d c e s t u z h g 6

Up-Tree: Unione a d c e h s t u z g 7

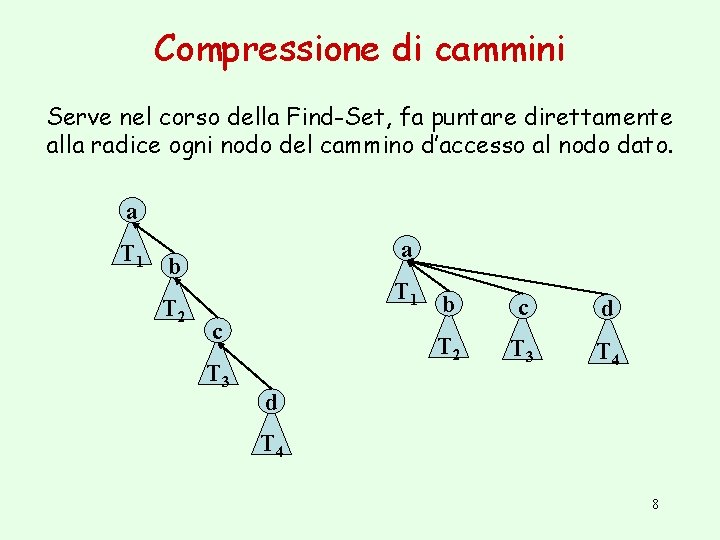
Compressione di cammini Serve nel corso della Find-Set, fa puntare direttamente alla radice ogni nodo del cammino d’accesso al nodo dato. a T 1 a b T 2 T 1 c T 3 b c d T 2 T 3 T 4 d T 4 8
![Algoritmi per uptree Si associa ad ogni nodo x un intero rankx limite superiore Algoritmi per up-tree Si associa ad ogni nodo x un intero rank[x], limite superiore](https://slidetodoc.com/presentation_image_h/d05b46737db3f79a4ab9ccc7b5af627b/image-9.jpg)
Algoritmi per up-tree Si associa ad ogni nodo x un intero rank[x], limite superiore all’altezza di x (num. archi del cammino più lungo fra x e una foglia discendente). Make-Set(x) p[x] = x rank[x]=0 Union(x, y) Link(Find-Set(x), Find-Set(y)) Link(x, y) if rank[x] > rank[y] then p[y] = x else p[x] = y if rank[x] == rank[y] then rank[y]++ Find-Set(x) if x ≠ p[x] then p[x] = Find-Set(p[x]) return p[x] 9

Up-Tree - sommario Make. Set (1) Find (h) Union (1) 10

Esponenziali di esponenziali F(0) = 1 F(i) = 2 F(i– 1) per ogni i > 0 F(1) = 21 = 2 F(2) = 22 = 4 F(3) = 2 2 2 F(4) = 2 22 F(5) = 2 = 16 2 2 = 65536 2 = 265536 1019728 Tutti i numeri incontrati normalmente sono più piccoli di F(5) 11

log* log n = il più piccolo i tale che F(i) n = = il più piccolo i tale che log log n 1. i volte log n 5 per ogni numero n incontrato in pratica 12

La funzione di Ackerman A(1, j ) = 2 j per j 1 A(i, 1 ) = A(i – 1, 2 ) per i > 1 A(i, j ) = A(i – 1, A(i, j – 1)) per i, j > 1 Inversa della funzione di Ackerman (per m n): (m, n) = il più piccolo i 1 tale che A(i, m/n ) > log n (m, n) 4 per ogni valore comune di m e n 13
![UpTree complessità Lemma 1 Per tutte le radici x di alberi sizex 2 Up-Tree: complessità Lemma 1 Per tutte le radici x di alberi, size[x] ≥ 2](https://slidetodoc.com/presentation_image_h/d05b46737db3f79a4ab9ccc7b5af627b/image-14.jpg)
Up-Tree: complessità Lemma 1 Per tutte le radici x di alberi, size[x] ≥ 2 rank[x] Lemma 2 Per ogni intero r≥ 0 ci sono al più n/2 r nodi di rango r. 14

Up-Tree: complessità Teorema Una sequenza di m operazioni Make-Set, Link e Find-Set, di cui n sono operazioni Make-Set, può essere eseguita su una foresta di up -tree con unione per rango e compressione di cammini in tempo O(m log n). Corollario Una sequenza di m operazioni Make-Set, Union e Find-Set, di cui n sono operazioni Make-Set, può essere eseguita su una foresta di up -tree con unione per rango e compressione di cammini in tempo O(m log n). 15
 Insiemi disgiunti
Insiemi disgiunti Insiemi disgiunti
Insiemi disgiunti Introduzione agli algoritmi e strutture dati
Introduzione agli algoritmi e strutture dati Cntrb
Cntrb Sottoinsiemi disgiunti
Sottoinsiemi disgiunti Poesia figure metriche
Poesia figure metriche Tdc significato pedagogico
Tdc significato pedagogico Struttura funzionale esempio
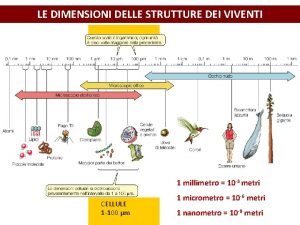
Struttura funzionale esempio Le dimensioni delle strutture dei viventi
Le dimensioni delle strutture dei viventi Chemiotassi
Chemiotassi Analisi non lineare delle strutture
Analisi non lineare delle strutture Strutture culturali
Strutture culturali Esempio piano di manutenzione delle strutture ntc 2018 doc
Esempio piano di manutenzione delle strutture ntc 2018 doc Spiccato di fondazione
Spiccato di fondazione Cadiprof strutture convenzionate
Cadiprof strutture convenzionate Nova angeletta sovra l'ale accorta parafrasi
Nova angeletta sovra l'ale accorta parafrasi