Gli insiemi e i suoi elementi A 2

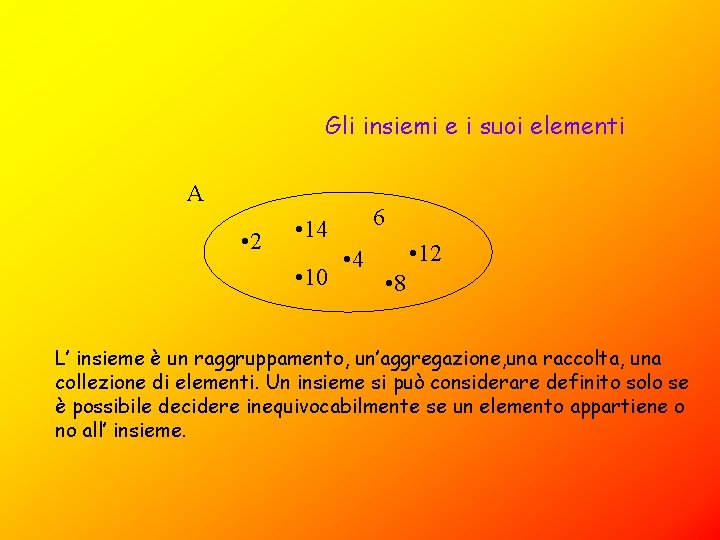
Gli insiemi e i suoi elementi A • 2 6 • 14 • 10 • 4 • 12 • 8 L’ insieme è un raggruppamento, un’aggregazione, una raccolta, una collezione di elementi. Un insieme si può considerare definito solo se è possibile decidere inequivocabilmente se un elemento appartiene o no all’ insieme.

Per indicare che un elemento a appartiene a un insieme A si usa il simbolo di appartenenza “ “ ; la scrittura “ a A “ si legge: “ a appartiene ad A “; per indicare che un elemento x non appartiene all’insieme A, si scrive “ x A “ e si legge “ x non appartiene ad A “. Generalmente gli insiemi si indicano con lettere maiuscole: A, B, C, …, X, Y, …; i suoi elementi invece con lettere minuscole: a, b, c, …, x, y, …. COME SI PUO’ RAPPRESENTARE UN INSIEME… Un insieme si rappresenta in tre modi diversi: con il diagramma di Eulero-Venn una rappresentazione geometrica di cui si delimita con una linea chiusa una regione del piano. A • 2 • 4 • 6

Per rappresentazione estensiva o per elencazione: consiste nell’elencare gli elementi tra parentesi graffe; A= 2, 4, 6 Per rappresentazione intensiva o per caratteristica: A= x x è un multiplo di 2 Insieme vuoto, sottoinsiemi e Insieme Universo Un insieme è vuoto quando contiene nessun elemento e si può indicare in due modi: o 0 Un sottoinsieme si verifica quando ogni elemento di B appartiene anche ad A. I sottoinsiemi si distinguono in propri e impropri. Sono del primo caso tutti quelli che non sono vuoti e che contengono alcuni elementi di A che non appartengono a B. Rispettano invece il secondo caso se si tratta dell’ insieme stesso o di un’ insieme vuoto. L’insieme universo viene indicato generalmente con la lettera “U” ed è l’ambiente da cui trarre gli elementi x dell’ insieme.

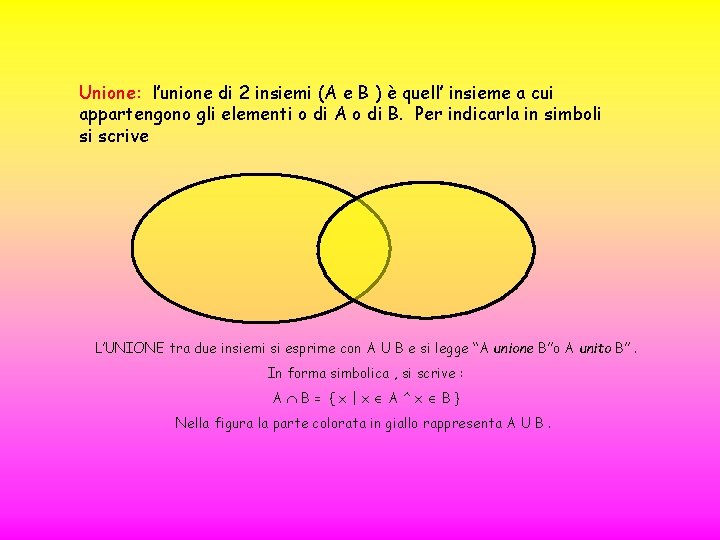
Unione: l’unione di 2 insiemi (A e B ) è quell’ insieme a cui appartengono gli elementi o di A o di B. Per indicarla in simboli si scrive L’UNIONE tra due insiemi si esprime con A U B e si legge “A unione B”o A unito B”. In forma simbolica , si scrive : A B= {x|x A^x B} Nella figura la parte colorata in giallo rappresenta A U B.

Intersezione: Dati 2 insiemi A e B, si definisce intersezione l’insieme degli elementi appartenenti sia ad A sia a B. L’intersezione tra due insiemi si esprime con A B e si legge “A intersezione B”o A intersecato B”. Usando i simboli, invece, si scrive A B= {x|x A^x B} Nella figura la parte colorata in rosso rappresenta A B. Esempio Dati gli insiemi A = { a, b, c, d, e } e B = { e, d, f, g, h, m } Quando l’intersezione tra A e B è un insieme vuoto si dice che questi due insiemi sono DISGIUNTI

L’intersezione e l’ unione godono delle proprietà commutativa e della proprietà associativa: A B=B A A (B C) = (A B) C = AUB= BUA AU(B UC ) = (AUB) UC

Insieme complementare. Si definisce complementare di un insieme A, rispetto ad un insieme ambiente , l’ insiemi degli elementi di U che non appartengono ad A. U Cu. A A Differenza. Si definisce differenza di due insiemi A e B, l’insieme costituito dagli elementi di A che non appartengono a B. A-B= {x | x A ^ x B}

Partizione. Tutti i sottoinsiemi formano una partizione di A se rispettano 3 condizioni : Ai Ak =0 , essendo i = Ai = k 0 A 1 U A 2 U… U An = A Prodotto Cartesiano Il prodotto cartesiano o insieme prodotto di A per B è l’ insieme di tutte le coppie ordinate (a, b) aventi per prima componente un elemento a A e per seconda componente un elemento b B. Molto importante da ricordare è il fatto che per questa operazione non vale la proprietà commutativa. Il prodotto cartesiano in simboli si rappresenta in diversi modi: 1. FORMA ESTENSIVA A X B ={(a, b)|a A, b B} 2. 3. 4. CON IL DIAGRAMMA CARTESIANO

Per il prodotto cartesiano è possibile anche avere 3 o più insiemi, come per esempio: A X B X C ={(a, b, c)|a A, b B, c C} e si può rappresentare più comodamente e facilmente con un diagramma ad albero. 1° componente 2° componente a b x (x, a) (x, b) c y Gli elementi di AXB (x, c) a (y, a) b (y, b) c (y, c)