Introduzione allAnalisi dei Dati LAnalisi Multidimensionale dei Dati

Introduzione all’Analisi dei Dati

L'Analisi Multidimensionale dei Dati Grazie ai progressi dell’informatica e alla maggiore disponibilità di dati, negli anni ‘ 60 la Statistica incomincia un processo di rinnovamento che modifica profondamente i rapporti fra teoria (modello) ed osservazione (dati). Nasce l’analisi dei dati. Uno dei nuovi approcci è quello che va sotto il nome di scuola francese di analisi multidimensionale dei dati (AMD) ed è legato al nome di J. P. Benzécri.

Statistica e Analisi dei Dati Statistica classica: Obiettivo confermativo (modello-dati) campione casuale – inferenza statistico Analisi dei Dati: Obiettivo esplorativo (dati-modello) EDA, J. Tukey Descrittivo (dati-struttura) AMD, J. P. Benzécri

Risultati di un’AMD L’AMD si propone di interpretare e visualizzare la struttura di fenomeni complessi mediante il trattamento di numerose variabili e osservazioni. Fornisce, infatti: • la visualizzazione di associazioni anche complesse • la definizione di fattori multidimensionali • la costruzione di tipologie di osservazioni • il disegno di mappe

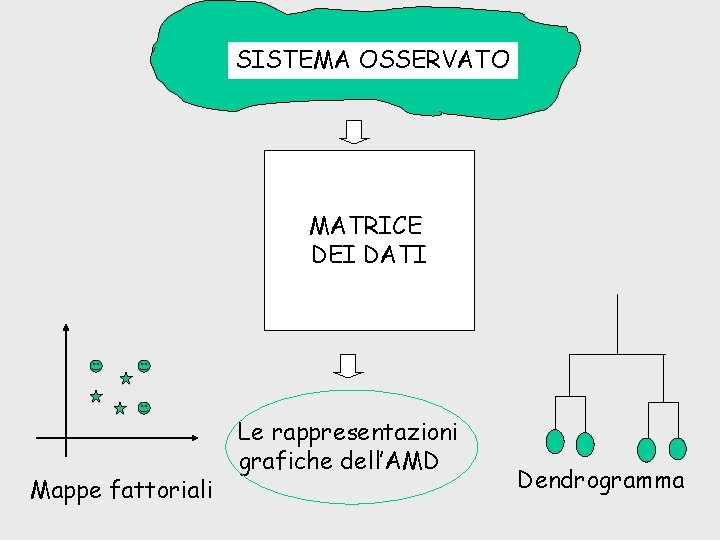
SISTEMA OSSERVATO MATRICE DEI DATI Mappe fattoriali Le rappresentazioni grafiche dell’AMD Dendrogramma

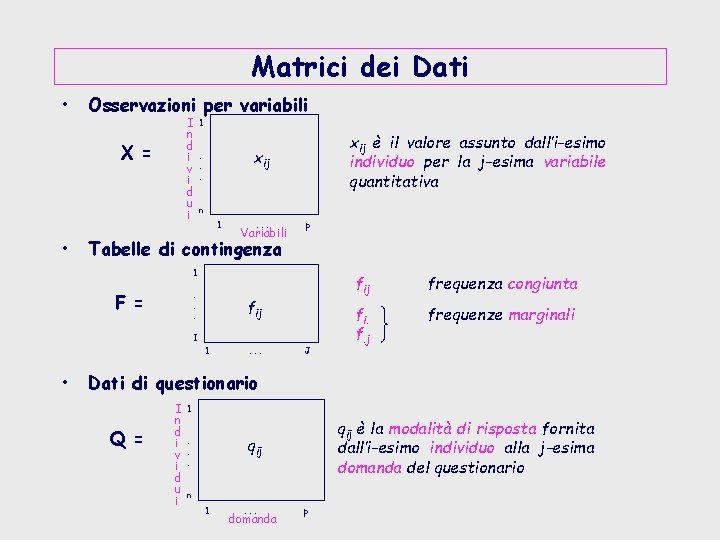
Matrici dei Dati • Osservazioni per variabili I n d i v i d u i X = • 1 xij è il valore assunto dall’i-esimo individuo per la j-esima variabile quantitativa xij . . . n 1 . . . Variabili p Tabelle di contingenza 1. . . F = fij I 1 • . . . J fij frequenza congiunta fi. f. j frequenze marginali Dati di questionario Q = I n d i v i d u i 1 qij è la modalità di risposta fornita dall’i-esimo individuo alla j-esima domanda del questionario qij . . . n 1 . . . domanda p

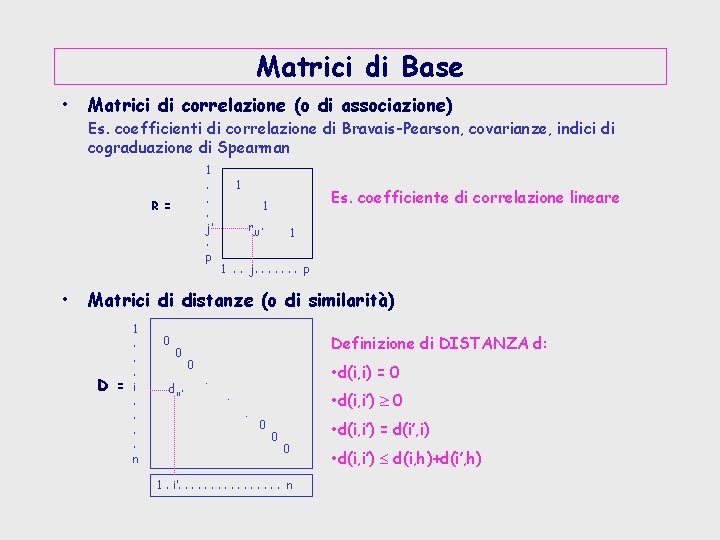
Matrici di Base • Matrici di correlazione (o di associazione) Es. coefficienti di correlazione di Bravais-Pearson, covarianze, indici di cograduazione di Spearman 1. . . j’. p R = • 1 Es. coefficiente di correlazione lineare 1 rjj’ 1 1. . j. . . . p Matrici di distanze (o di similarità) D = 1. . . i. . n 0 0 dii’ Definizione di DISTANZA d: 0 • d(i, i) = 0 . • d(i, i’) 0 . . 0 0 0 1. i’. . . . n • d(i, i’) = d(i’, i) • d(i, i’) d(i, h)+d(i’, h)

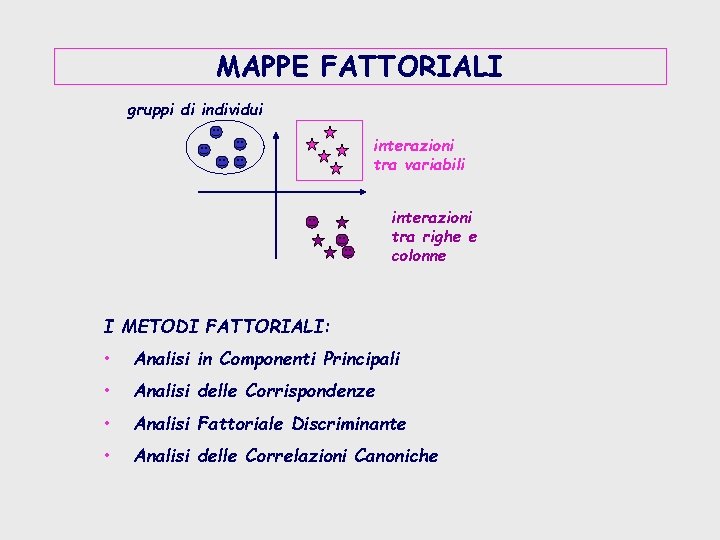
MAPPE FATTORIALI gruppi di individui interazioni tra variabili interazioni tra righe e colonne I METODI FATTORIALI: • Analisi in Componenti Principali • Analisi delle Corrispondenze • Analisi Fattoriale Discriminante • Analisi delle Correlazioni Canoniche

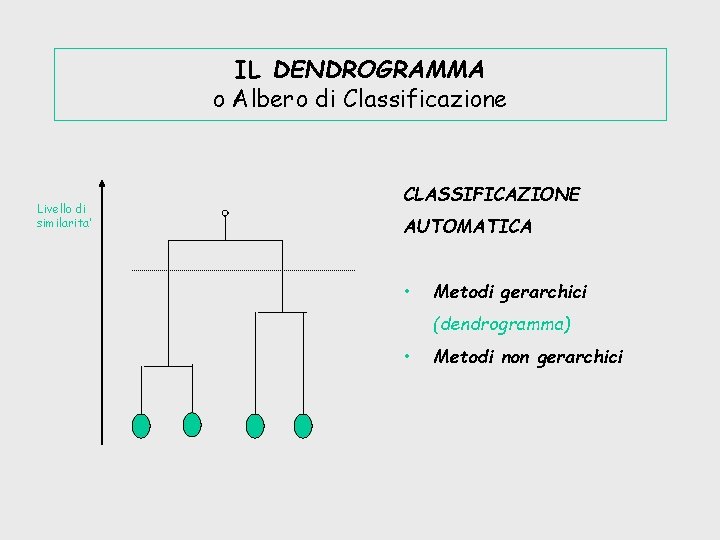
IL DENDROGRAMMA o Albero di Classificazione Livello di similarita’ CLASSIFICAZIONE AUTOMATICA • Metodi gerarchici (dendrogramma) • Metodi non gerarchici

Vettori (richiami) Un vettore reale a di dimensione n è un insieme di n numeri reali a 1, …, ai, …, an , detti componenti di a a = a 1, …, ai, …, an aa = aa 1, …, aai, …, aan • a=b • a±b = • a +b =b +a • (a + b) + c = a + (b + c) • (a + b) a = aa + ba • a (a + b ) = aa + a b • aa + bb scalari a costante sse ai = bi i a 1 + b 1, …, ai + bi, …, an +bn è detta combinazione lineare dei vettori a e b, con a e b

Vettori come punti • Struttura algebrica somma x 1 + x 2 : x 1 + x 2 x 1 = 4 2 x 2 = 2 5 x 1 + x 2 = 6 7 ½y = 2 1 2 y = 8 4 x 2 = 3 1 x 3 = 3 4 x 1 • Moltiplicazione per uno scalare: 2 y y= 42 ½y y • Centroide g = 1/n ixi x 1+x 2+x 3 x 1 g x 3 x 2 x 1 = 0 2 x 1 + x 2 + x 3 = 6 7 g = 2 2, 3

Rappresentazione geometrica NORMA (= lunghezza) di a: ||a|| = (a 12 + a 22 + … + an 2)½ DISTANZA fra a e b d 2(a, b): ||a-b||2= (a 1 -b 1)2 + … +(an -bn)2 a b PRODOTTO SCALARE di a e b a’b = a 1 b 1 + a 2 b 2 + … + anbn Allora: ||a||2=a’a e ||a||=0 vettore nullo Se a’b = 0 a e b sono ortogonali L’angolo ab fra a e b, vettori non nulli, è definito da: cos( ab) = a’b/||a||||b||

Spazio euclideo Dato un insieme di p vettori n dimensionali a 1, …, ap essi sono detti linearmente indipendenti se per valori c 1, …, cp c 1 a 1 + … + cp ap = 0 c 1 = … = cp = 0 Se non sono linearmente indipendenti sono linearmente dipendenti, ovvero se esiste un insieme di numeri reali c*1, …, c*p non tutti uguali a 0, per i quali c*1 a 1+ … + c*p ap= 0 In altri termini, i vettori a 1, …, ap sono linearmente dipendenti sse uno di loro è uguale ad una combinazione lineare degli altri. Un sotto insieme V dello spazio euclideo En è detto sottospazio lineare se: e a V b V a V e valore reale a , (a + b) V aa V La dimensione di V, dim(V), è data dal numero di vettori linearmente indipendenti in V.

Basi ortogonali E’ detto BASE di V l’insieme degli r vettori B = (b 1, …, br) linearmente indipendenti , con r = dim(V) Se per una BASE B* = (b*1, …, b*r), b*’i b*i’ = 0 i i’ allora B* è detta BASE ORTOGONALE di V Se ||b*i||= 1 i allora B* è detta BASE ORTONORMALE di V Ogni sottospazio vettoriale è generato da una sua base ed ha una base ortonormale Es. di base ortogonale in 2: b 1 = 1 0 b 2 = 0 1 b 2 0 2 b 1 Es. x = 3 2 y = 4 -6 sono una base ortogonale «Una base è ortogonale se i suoi vettori sono ortogonali a coppie»

Proiezioni ortogonali in un sottospazio Si consideri un sottospazio di dimensione 1, generato da un vettore v di norma unitaria: ||v|| = 1. Si voglia proiettore un punto x di dimensione p > 1. La coordinata a del punto x*, proiezione ortogonale (x v) di x su v è data da: x a = x’v. v x* Poniamo x* = av. L’ortogonalità implica che: (x-x*)’v = 0 x’v - x*’v = 0 x’v - av’v = 0 La coordinata a è una combinazione lineare: a = x 1 x 2 ‘ v 1 v 2 = x 1 v 1 + x 2 v 2 a = x’v

Autovalori e autovettori A (p, p) x u (p) =l u (p) (richiami 1. ) Au= l u l autovalore u autovettore Per una matrice A quadrata, una costante l ed un vettore u che soddisfano la seguente condizione sono chiamati autovalore e autovettore di A (o, rispettivamente, radice caratteristica o latente e vettore caratteristico o latente: Au = l u da cui (A-l I)u = 0 (con I matrice Identità) | A-l I | = 0 equazione caratteristica

Autovalori e autovettori ua (p) (richiami 2. ) • se u’ u=1, allora si dice che u è normalizzato • la somma degli autovalori è pari ala traccia della matrice la A (p, p): U = Il caso di matrici simmetriche: u 1 ua up • Gli autovalori sono reali, positivi o nulli: l 1 l 2 . . . la . . . lp 0 • Gli autovettori sono ortogonali: u’a ub = 0 e, quindi, se U è la matrice che ha in colonna i p autovettori di A: U’U=Ip=UU’ U’=U-1 (idempotenza) inoltre

Autovalori e autovettori (richiami 3. ) Ancora, se A è simmetrica, di ordine p (il rango di A, rang(A)=p), con l 1> l 2>. . . > la >. . . > lp> 0 (autovalori distinti), cui corrispondono gli autovettori di norma unitaria u 1, u 2, . . . , ua , . . . , up , che formano la matrice idempotente U, precedentemente definita, allora: l 1 -1 UAU = L = . . . la. . . lp da cui: A = U-1 LU, che è detta decomposizione spettrale di A