Randomized Algorithms Data Structures 12122021 Randomized Algorithms Treaps

Randomized Algorithms: Data Structures 12/12/2021 Randomized Algorithms - Treaps 1

Randomized Treaps n n Treap = TREe he. AP Or, In Hebrew: ערמה עץ = ערמץ 12/12/2021 Randomized Algorithms - Treaps 2

Outline 12/12/2021 n Definition of the Problem n Deterministic Data Structures n Introducing: Treaps n Analyzing Performance n Conclusion Randomized Algorithms - Treaps 3

Definition of the Problem n Maintain a collection of items. n Each of which is given a unique key. n Support a group of 7 operations and queries over these items: 12/12/2021 Randomized Algorithms - Treaps 4

12/12/2021 n Make. Set(S) n Find(k, S) n Insert(k, S) n Join(S 1, k, S 2) Randomized Algorithms - Treaps 5

12/12/2021 n Delete(k, S) n Paste(S 1, S 2) n Split(k, S) Randomized Algorithms - Treaps 6

Deterministic Data Structures Binary Search Trees n A standard solution to the problem. n For simplicity we will assume that the trees are endogenous, and thus, also full. 12/12/2021 Randomized Algorithms - Treaps 7

Binary Search Trees Performance Issues n Each of the 7 aforementioned operations could be implemented in o(H). n Ideally n Easy to devise an order of insertion in which 12/12/2021 . Randomized Algorithms - Treaps . 8

Binary Search Trees Possible Deterministic Improvements n Balancing the bst ¨ using rotations at each update operation. n Drawback ¨ Could render significant overhead at each update operation. 12/12/2021 Randomized Algorithms - Treaps 9

n Splaying: ¨ Move to the root a node accessed by find. n Analysis: ¨ Guarantees an amortized time bound of o(log n). 12/12/2021 Randomized Algorithms - Treaps 10

n Drawback: ¨ Restructuring of the tree at each find operation. ¨ No assurance that a specific action will take a certain amount of time. 12/12/2021 Randomized Algorithms - Treaps 11

Introducing: Treaps n Consider a binary tree where each node v contains a pair of values (both should be distinct from other nodes) : ¨ a key – should suffice the binary search condition. ¨ a priority – should suffice the heap condition. 12/12/2021 Randomized Algorithms - Treaps 12

n For Example: the set could be represented by the valid treap: 7, 30 4, 26 2, 13 12/12/2021 11, 27 12, 22 Randomized Algorithms - Treaps 13

Treaps implementation (in brief) n All operations are implemented in a similar way to the BST solutions available. n When an action violates heap condition, use rotations. 12/12/2021 Randomized Algorithms - Treaps 14

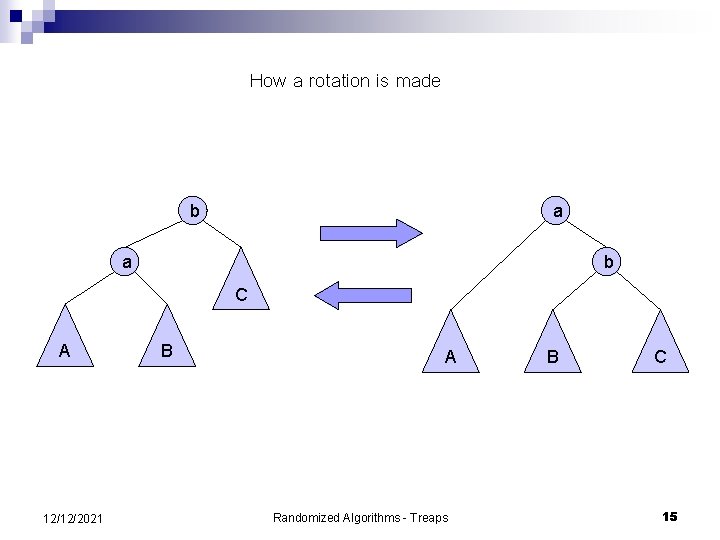
How a rotation is made b a a b C A 12/12/2021 B A Randomized Algorithms - Treaps B C 15

n Note, for future analyzing purposes, that all operations could be based upon find, insert and delete operations. 12/12/2021 Randomized Algorithms - Treaps 16

On choosing priorities n Theorem: Let S= be any set of key-priority pairs such that the keys and the priorities are distinct. Then, there exist a unique treap T(S) for it. 12/12/2021 Randomized Algorithms - Treaps 17

n Proof: By induction: ¨ 12/12/2021 for n=0, n=1: theorem holds. Randomized Algorithms - Treaps 18

¨ for n>1: without the loss of generality, assume that V = (k 1, p 1) is the node with the highest priority: 12/12/2021 n Assign V to root. n recursively apply on both sub trees emerging from splitting by p 1. Randomized Algorithms - Treaps 19

n The theorem implies that we may choose any (distinct) priorities to our nodes, ensuring that are we are representing a valid treap. 12/12/2021 Randomized Algorithms - Treaps 20

n We will choose our priorities in the following manner: ¨ Upon insertion of a new key, a priority is randomly and uniformly chosen for it, in such a way that no previous node contains this priority. ¨ The priority for a specific element remains constant. ¨ The ordering of 12/12/2021 keys and values is completely uncorrelated. Randomized Algorithms - Treaps 21

Analyzing Performance Mulmuley Games n For the sake of time performance, we will present a set of games, called Mulmuley Games. 12/12/2021 Randomized Algorithms - Treaps 22

Mulmuley Games Game A n Participants: ¨ A set of players. Each assigned a distinct numerical key. ¨ A set of bystanders. Each assigned a distinct numerical key. 12/12/2021 Randomized Algorithms - Treaps 23

n The course of the game consists of repeatedly sampling from P union B. Without replacement, until the pool is empty. n A random variable V is defined as the number of samples in which a player p is chosen such that p is the largest player chosen to this point. n The value of the game Ap is E[V]. 12/12/2021 Randomized Algorithms - Treaps 24

n Lemma: for all p > 0, Ap = Hp. 12/12/2021 Randomized Algorithms - Treaps 25

Mulmuley Games Game D n Participants: ¨ A set of players. Each assigned a distinct numerical key. ¨ A set of bystanders. Each assigned a distinct numerical ¨ A set of triggers. Each assigned a distinct numerical key. 12/12/2021 Randomized Algorithms - Treaps 26

n The course of the game consists of repeatedly sampling from P union B union T. Without replacement, until the pool is empty. n A random variable V is defined as the number of samples in which a player p is chosen such that p is the largest player chosen to this point. Only after a trigger was chosen. n The value of the game 12/12/2021 is E[V]. Randomized Algorithms - Treaps 27

n Lemma: 12/12/2021 Randomized Algorithms - Treaps 28

Analyzing Performance n We will present and prove several theorems, regarding time bounds of operations on random treaps. n For the following, assume that T is a random treap for a set S of size n. 12/12/2021 Randomized Algorithms - Treaps 29

n Theorem: The expected time for find, insert and delete operations on T is O(log n). 12/12/2021 Randomized Algorithms - Treaps 30

n n Lemma: for an element of rank k (regarding its key), it holds that: The lemma implies that the depth of each element is o(log n) each of the operations ( find, insert and delete) are linear in reagards to the tree depth, it follows that they also are o(log n). 12/12/2021 Randomized Algorithms - Treaps 31

n Proof of the lemma: let us define: 12/12/2021 Randomized Algorithms - Treaps 32

- Ancestors of x 12/12/2021 Randomized Algorithms - Treaps 33

§ it is clear that : depth(x) = § And thus E[depth(x) ] = § Therfore, we will try and estimate and 12/12/2021 Randomized Algorithms - Treaps 34

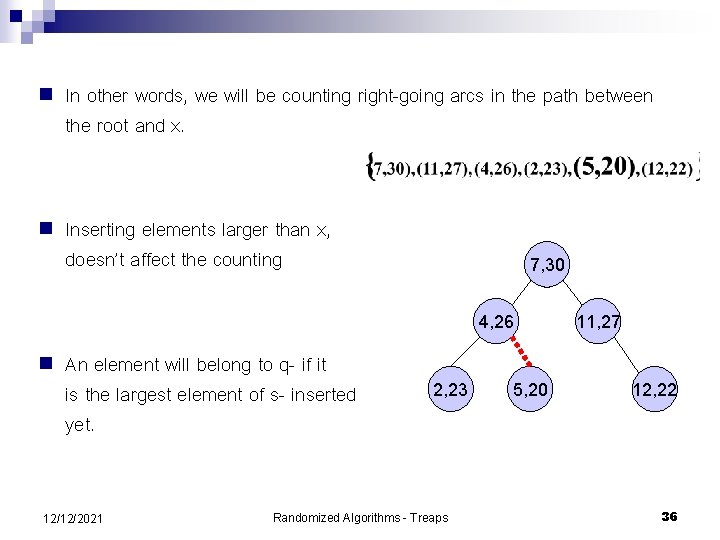
n Let us write S= (hence p 1 > p 2 > … > pn) n We will insert the elements into the tree by this order (notice that no rotations are needed) n When will an element belong to S- ? 12/12/2021 ordered by their priority. Randomized Algorithms - Treaps 35

n In other words, we will be counting right-going arcs in the path between the root and x. n Inserting elements larger than x, doesn’t affect the counting 7, 30 4, 26 n An element will belong to q- if it is the largest element of s- inserted yet. 12/12/2021 2, 23 Randomized Algorithms - Treaps 5, 20 11, 27 12, 22 36

n Notice that this resembles Game A with P = S- , B = SS- and thus p = k, following that n Similarly it can be shown that n Therefore 12/12/2021 Randomized Algorithms - Treaps 37

n Theorem: The expected number of rotations required during an insert or delete operation is at most 2. n We will prove that for each element x defined as before, it holds that the number of rotations is 2. 12/12/2021 Randomized Algorithms - Treaps 38

n Proof: ¨ Let us define: Rx – the right spine of the left subtree of X. Lx – the left spine of the right subtree of X. ¨ Observation 1: the number of rotations needed during these operations is |Rx| + |Lx| 12/12/2021 Randomized Algorithms - Treaps 39

n In a similar to the one taken in the previous theorem, we can show that E[|Rx|] is in fact similar to Game D with p = k-1 , t = 1 , b = n – k Which yeilds that E[|Rx|] = 1 – 1/k. n It can also be shown, by the same method that E[|Lx|] = 1 – 1/(n-k+1). n Therefore E[|Lx|] + E[|Rx|] <= 2 12/12/2021 Randomized Algorithms - Treaps 40

n Theorem: The expected time for join, paste and split involving sets S 1 and S 2 of sizes n and m respectively, is o(log n + log m). 12/12/2021 Randomized Algorithms - Treaps 41