A Randomized Polynomial Time Simplex Algorithm for Linear

A Randomized Polynomial. Time Simplex Algorithm for Linear Programming CS 3150 Course Presentation

Linear Programming Example: ･Find the maximum value of p = 3 x - 2 y + 4 z ･subject to ･ 4 x + 3 y - z >= 3 ･x + 2 y + z<=4 ･ x >= 0, y >= 0, z >= 0

Linear Programming • Objective Function max z. T x • Constraints s. t. Ax£y

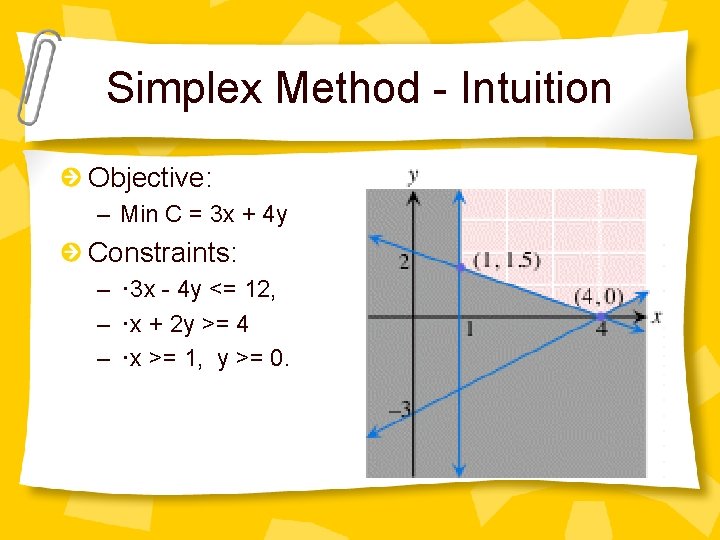
Simplex Method - Intuition Objective: – Min C = 3 x + 4 y Constraints: – ･ 3 x - 4 y <= 12, – ･x + 2 y >= 4 – ･x >= 1, y >= 0.

Simplex Method - Intuition max z. T x s. t. Ax£y • Worst-Case: exponential • Average-Case: polynomial • Widely used in practice

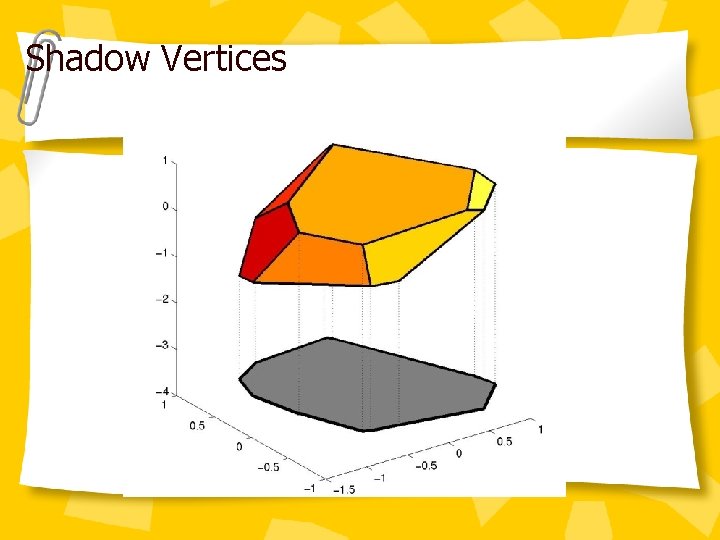
Shadow Vertices

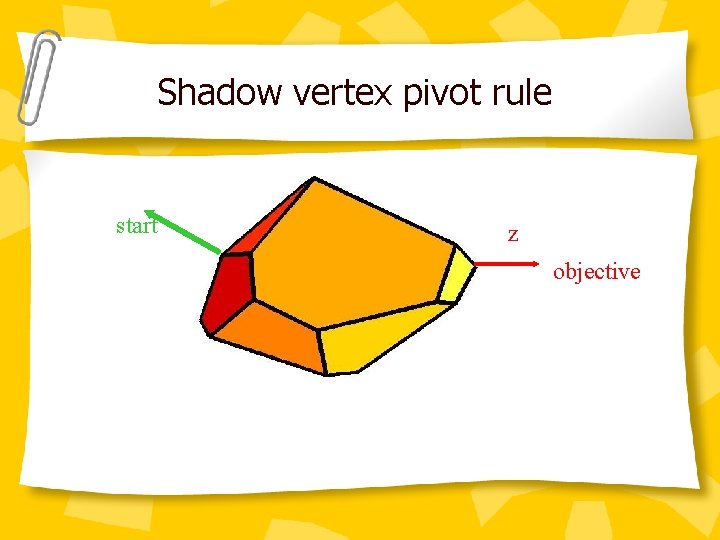
Shadow vertex pivot rule start z objective

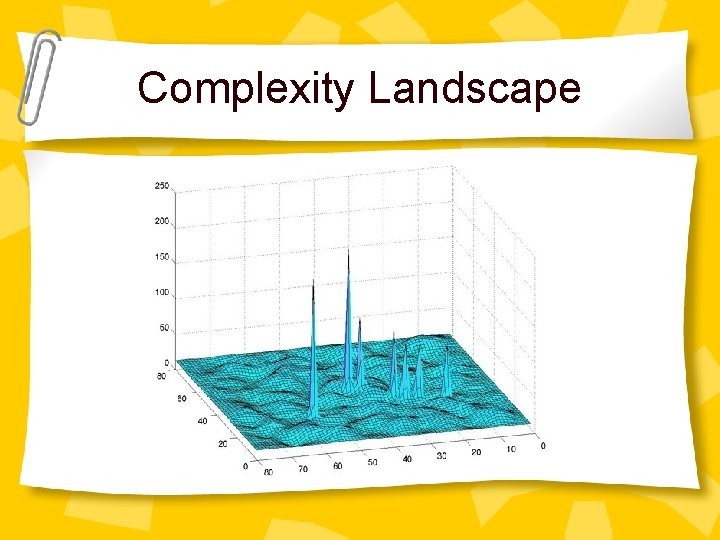
Complexity Landscape

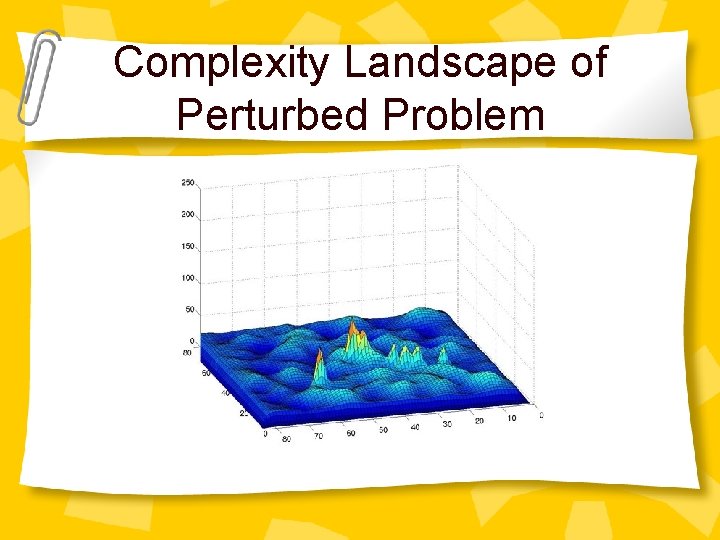
Complexity Landscape of Perturbed Problem

Some issues Problem max z. T x s. t. Ax£y – The perturbed problem is no longer the original problem we want to solve! Solution – Reduce the original problem to another problem, where the perturb won’t affect solution. – Is this set of constraints bounded? A’w<=1

Intuition of the Algorithm Since the right hand side won’t affect solution, we want to carefully choose it so that the Shadow-Vertex Simplex will run poly-time with high probability.

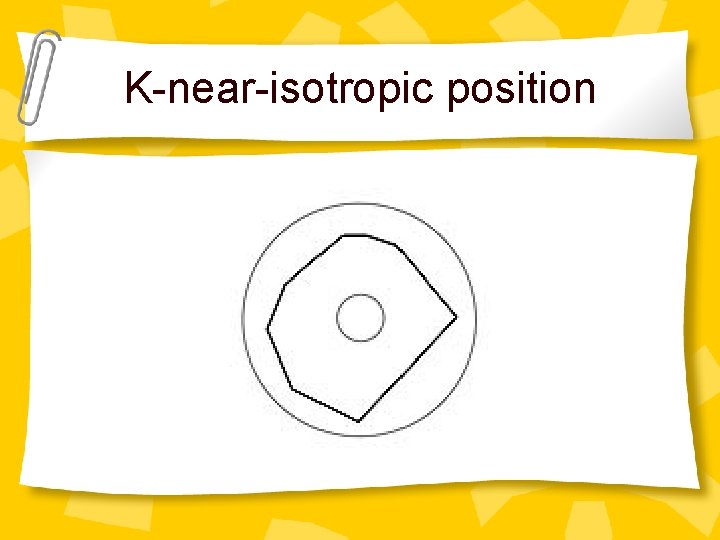
Intuition of the Proof P is the polytope of A’w<=1 Case 1: – The polytope P is in k-near-isotropic position

K-near-isotropic position

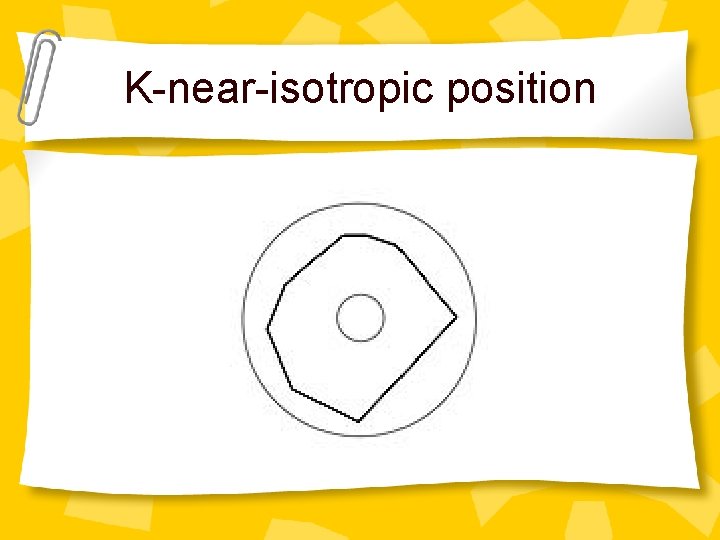
Intuition of the Proof Case 1: – The polytope is in k-near-isotropic position – Case 2: – The polytope is not in k-near-isotropic position

K-near-isotropic Case Upper bound of total shadow length (Shadow Size). Lower bound expected length of each edge. Number of edges of the shadow is poly in size w. h. p.

K-near-isotropic position

Randomization Each of vector is a independently exponentially distributed random variable with expectation Project onto a random plane

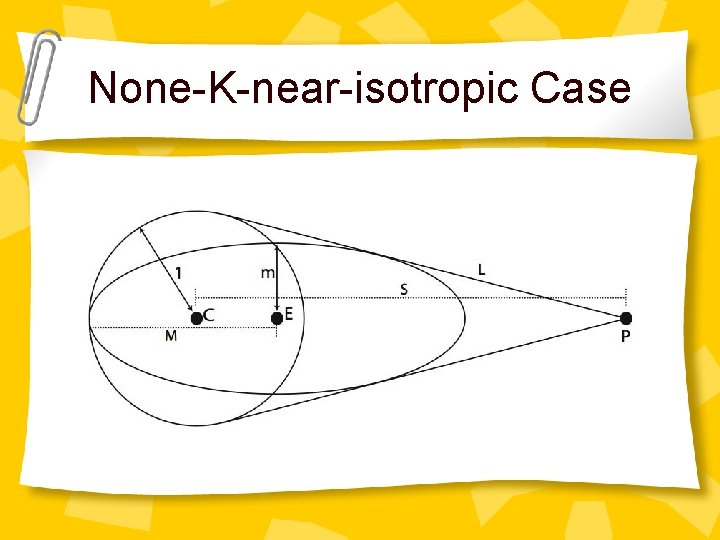
None-K-near-isotropic Case By Running the shadow vertex for a limited amount of time we can either: – Find the optimal – Or find a way to eliminate bad events w. h. p.

None-K-near-isotropic Case

K-near-isotropic Case Upper bound of the total shadow length. Lower bound the expected length of each edge. Number of edges of the shadow is poly in size w. h. p.

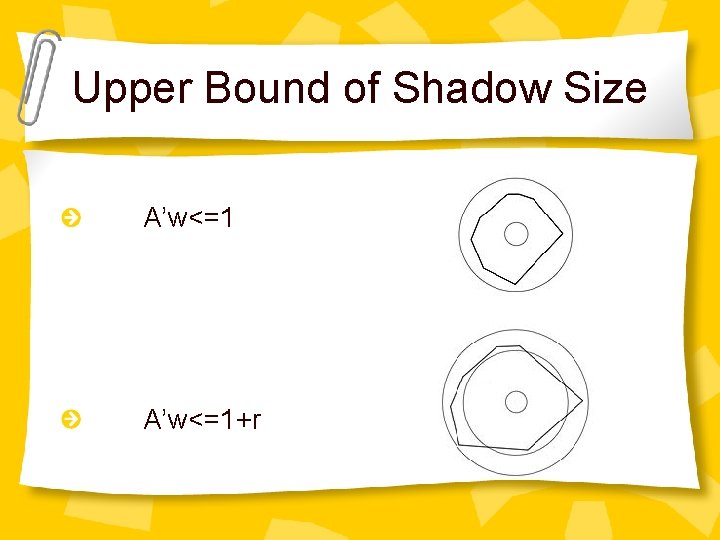
Upper Bound of Shadow Size A’w<=1+r

Shadow Size in Case 1 The expected shadow size is at most:

Upper Bound of Shadow Size

K-near-isotropic Case Upper bound of the total shadow length. Lower bound the expected length of each edge. Number of edges of the shadow is poly in size w. h. p.

Expected Edge Length The Expected Edge Length is at least:

Case 1 Main Theorem The expected number of edges is at most

None-K-Isotropic Case The expected shadow size inside any given ball is small

None-K-near-Isotropic Case Upper bound of the total shadow length within the given ball. Lower bound the expected length of each edge within the given ball. Number of edges of the shadow is poly in size w. h. p.

Outline of the Algorithm Run Shadow Vertex Simplex on the Randomized Input – If Find Optimal then halt Else transform the coordinates and run shadow vertex simplex on the transformed inputs Algorithm will halt in poly-time w. h. p.

Summery and Intuitions Deterministic algorithms run exponential time on some “bad” inputs By introducing some randomness into the algorithm fixed the problem. The Randomized algorithm run poly time on all inputs with high probability. Start with something strict, which is easy to prove the poly-bound, eliminate the bad events in poly-time.