Data Structures Algorithms Lecture 4 Data Structures Algorithms

Data Structures & Algorithms Lecture # 4

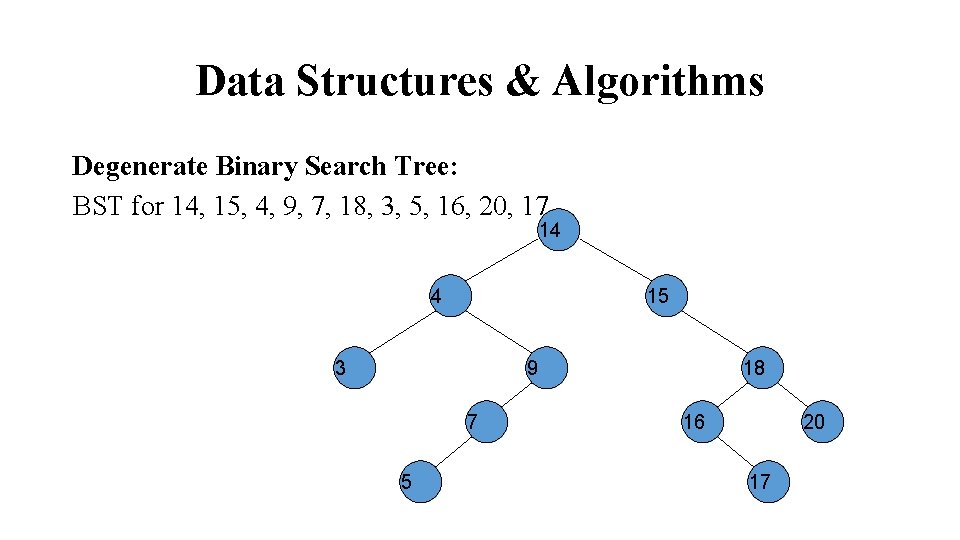
Data Structures & Algorithms Degenerate Binary Search Tree: BST for 14, 15, 4, 9, 7, 18, 3, 5, 16, 20, 17 14 4 15 3 9 7 5 18 16 20 17

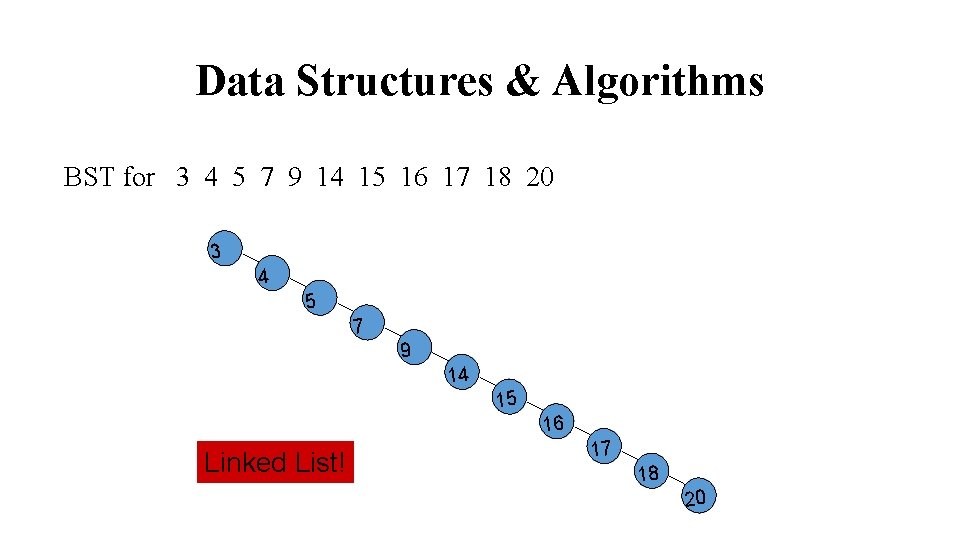
Data Structures & Algorithms BST for 3 4 5 7 9 14 15 16 17 18 20 3 4 5 7 9 14 15 16 Linked List! 17 18 20

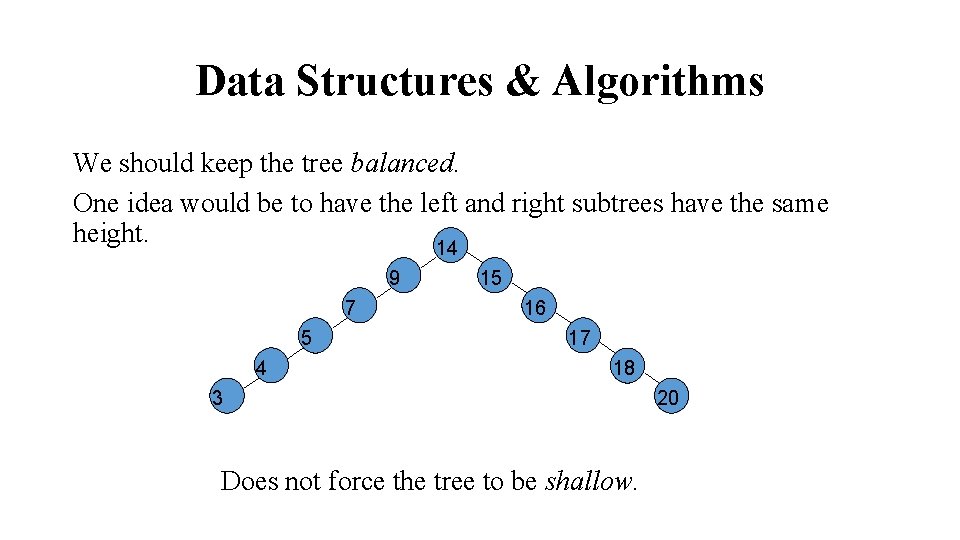
Data Structures & Algorithms We should keep the tree balanced. One idea would be to have the left and right subtrees have the same height. 14 9 7 5 4 15 16 17 18 3 Does not force the tree to be shallow. 20

Data Structures & Algorithms We could insist that every node must have left and right subtrees of same height. But this requires that the tree be a complete binary tree. To do this, there must have (2 d+1 – 1) data items, where d is the depth of the tree. This is too rigid a condition.

Data Structures & Algorithms AVL (Adelson-Velskii and Landis) tree. An AVL tree is identical to a BST except § height of the left and right subtrees can differ by at most 1. § height of an empty tree is defined to be (– 1).

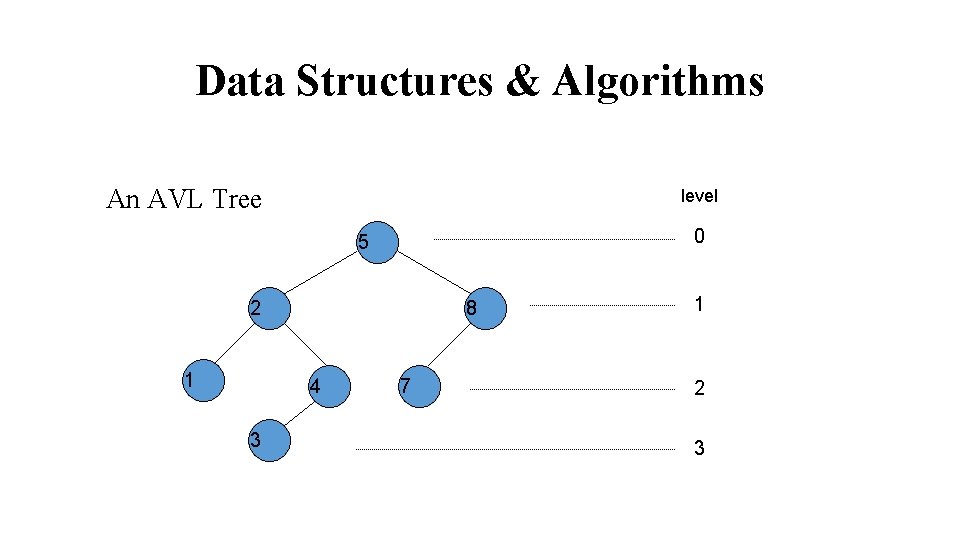
Data Structures & Algorithms An AVL Tree level 0 5 2 1 8 4 3 7 1 2 3

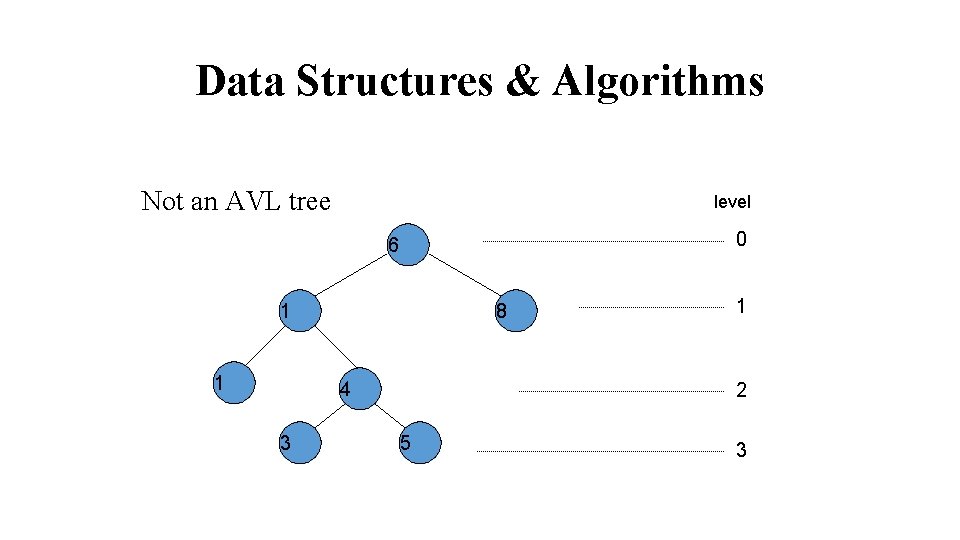
Data Structures & Algorithms Not an AVL tree level 0 6 1 1 8 4 3 1 2 5 3

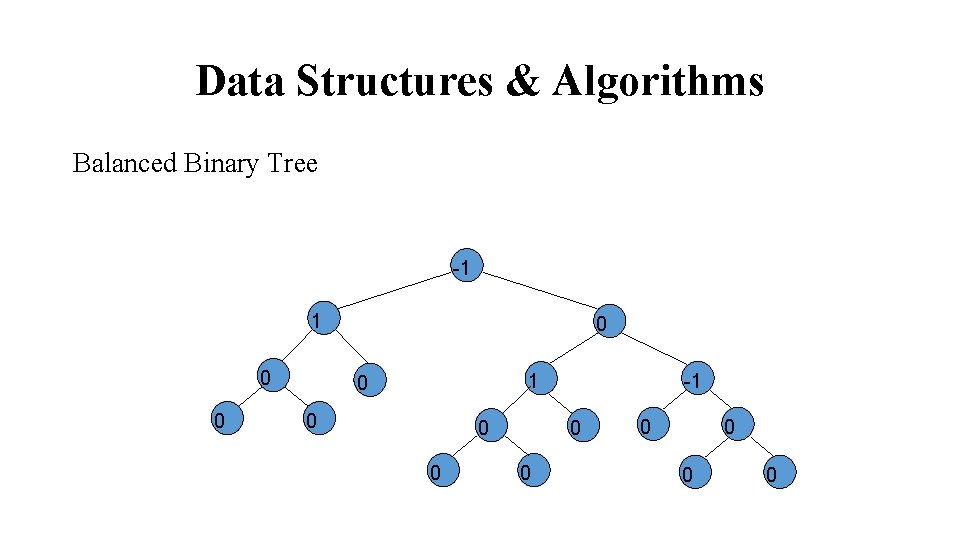
Data Structures & Algorithms The height of a binary tree is the maximum level of its leaves (also called the depth). The balance of a node in a binary tree is defined as the height of its left subtree minus height of its right subtree. Here, for example, is a balanced tree. Each node has an indicated balance of 1, 0, or – 1.

Data Structures & Algorithms Balanced Binary Tree -1 1 0 0 0 0

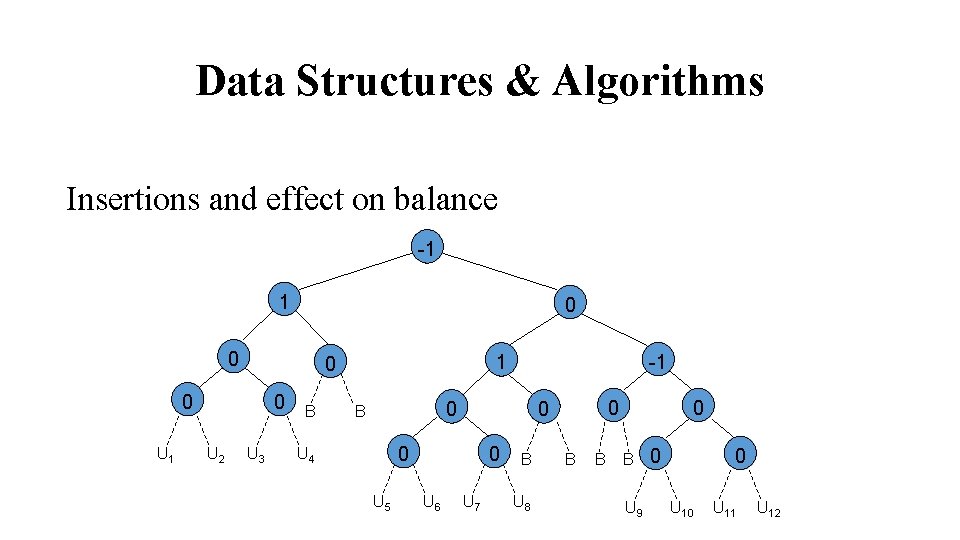
Data Structures & Algorithms Insertions and effect on balance -1 1 0 0 0 U 1 0 U 2 U 3 B -1 1 0 0 B 0 U 4 U 5 0 U 6 0 0 U 7 B U 8 B B 0 B U 9 0 0 U 11 U 12

Data Structures & Algorithms Tree becomes unbalanced only if the newly inserted node § is a left descendant of a node that previously had a balance of 1 (U 1 to U 8), § or is a descendant of a node that previously had a balance of – 1 (U 9 to U 12)

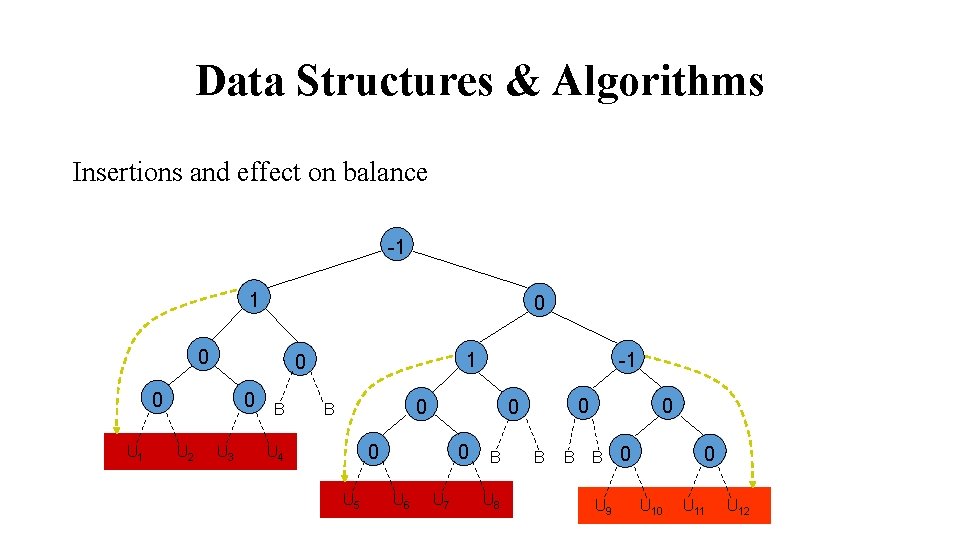
Data Structures & Algorithms Insertions and effect on balance -1 1 0 0 0 U 1 0 U 2 U 3 B -1 1 0 0 B 0 U 4 U 5 0 U 6 0 0 U 7 B U 8 B B 0 B U 9 0 0 U 11 U 12

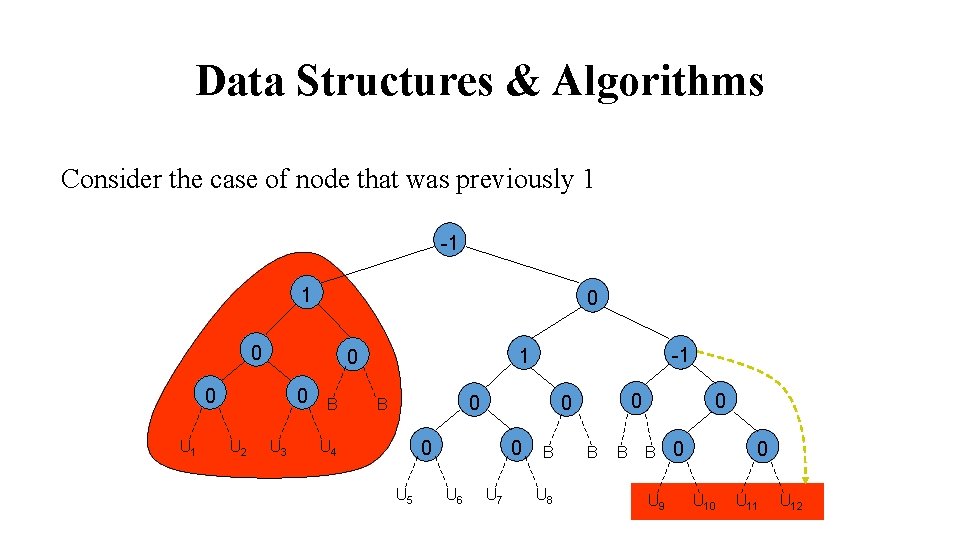
Data Structures & Algorithms Consider the case of node that was previously 1 -1 1 0 0 0 U 1 0 U 2 U 3 B -1 1 0 0 B 0 U 4 U 5 0 U 6 0 0 U 7 B U 8 B B 0 B U 9 0 0 U 11 U 12

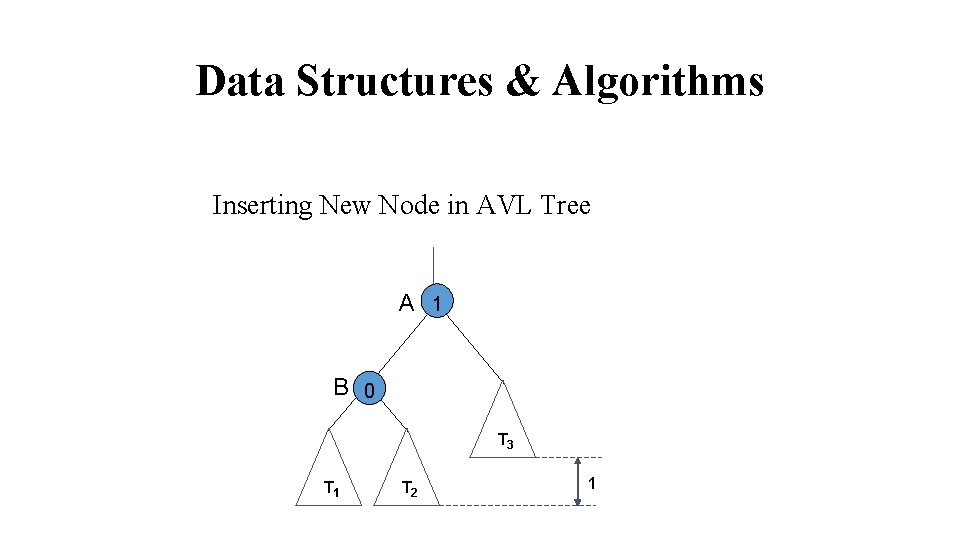
Data Structures & Algorithms Inserting New Node in AVL Tree A 1 B 0 T 3 T 1 T 2 1

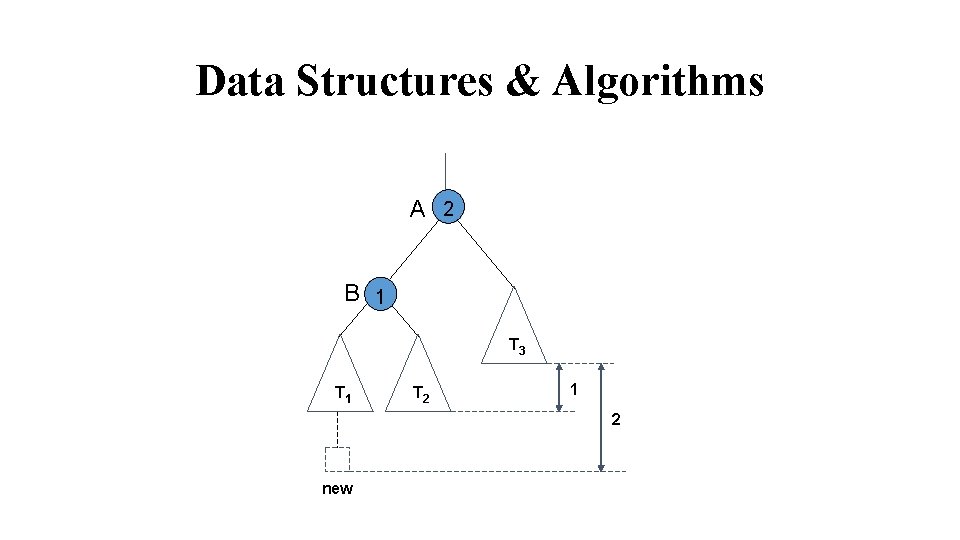
Data Structures & Algorithms A 2 B 1 T 3 T 1 T 2 1 2 new

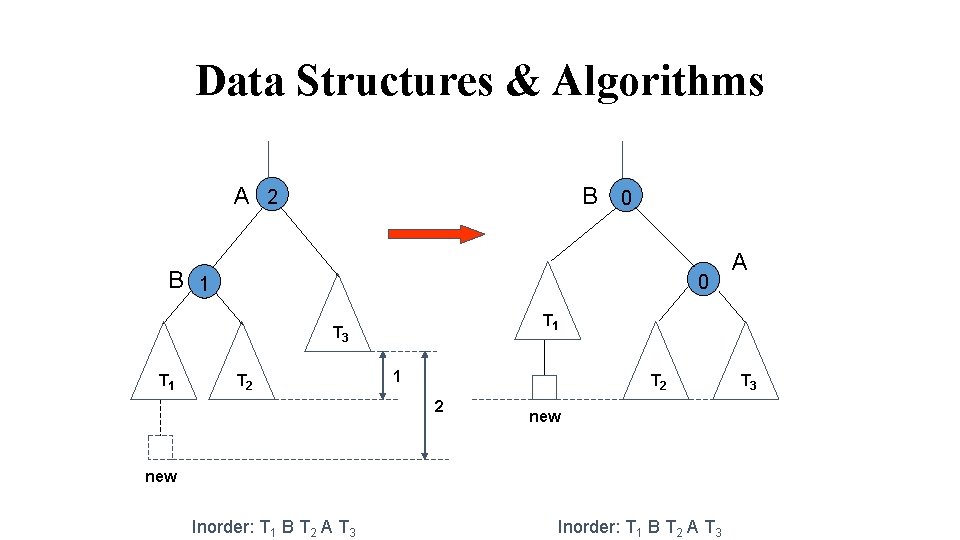
Data Structures & Algorithms A 2 B 0 B 1 0 T 1 T 3 T 1 T 2 2 new Inorder: T 1 B T 2 A T 3 A Inorder: T 1 B T 2 A T 3

Data Structures & Algorithms Let us work through an example that inserts numbers in a balanced search tree. We will check the balance after each insert and rebalance if necessary using rotations. AVL Tree Building Example Insert(1) 1

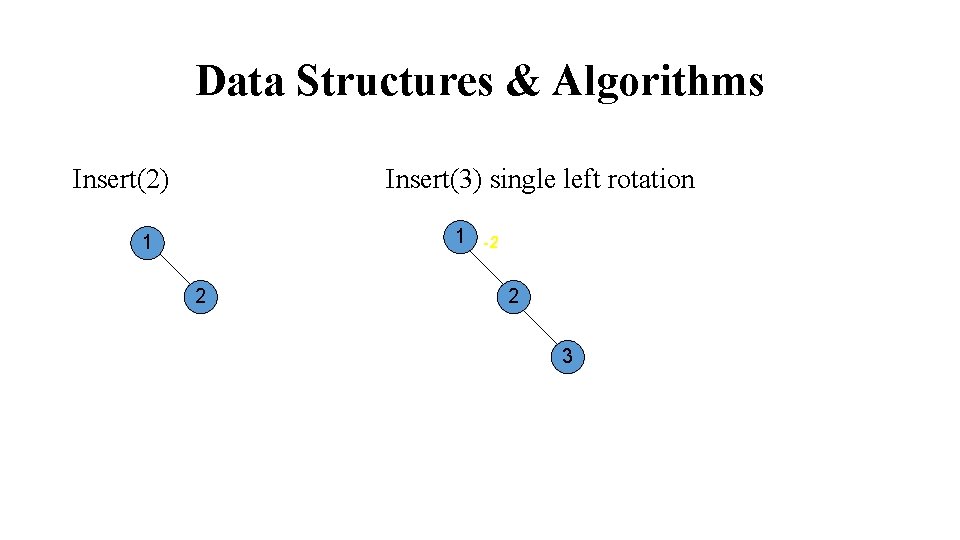
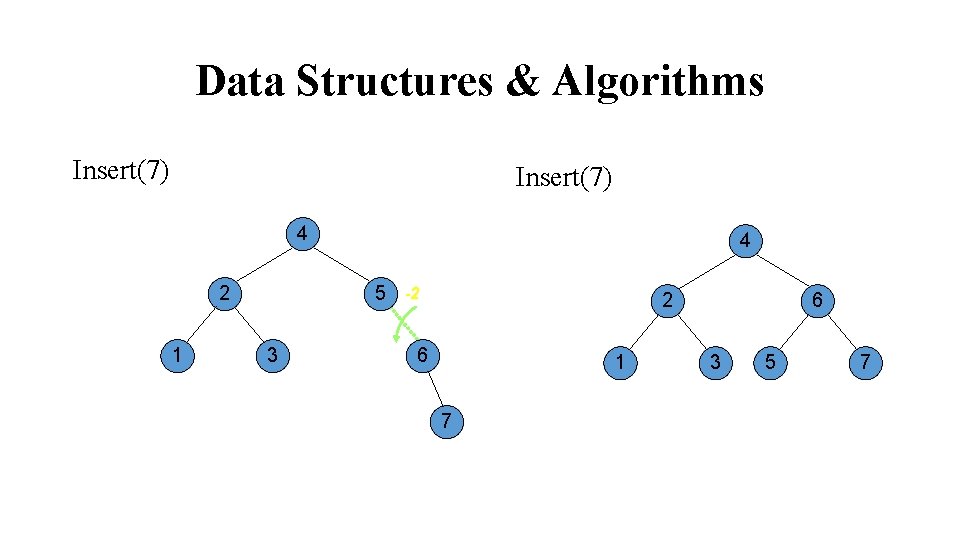
Data Structures & Algorithms Insert(2) Insert(3) single left rotation 1 1 2 -2 2 3

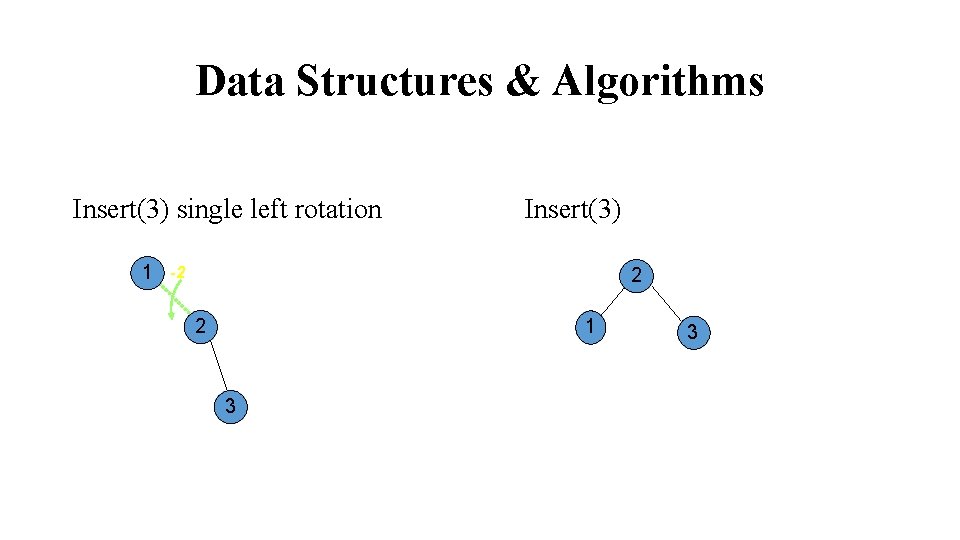
Data Structures & Algorithms Insert(3) single left rotation 1 Insert(3) 2 -2 2 1 3 3

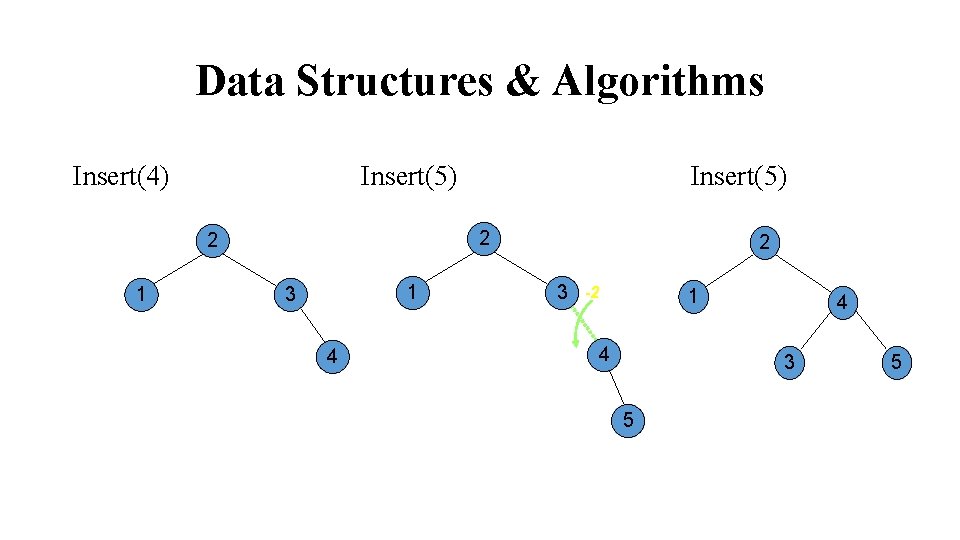
Data Structures & Algorithms Insert(5) Insert(4) 2 2 1 Insert(5) 1 3 4 2 3 -2 1 4 4 3 5 5

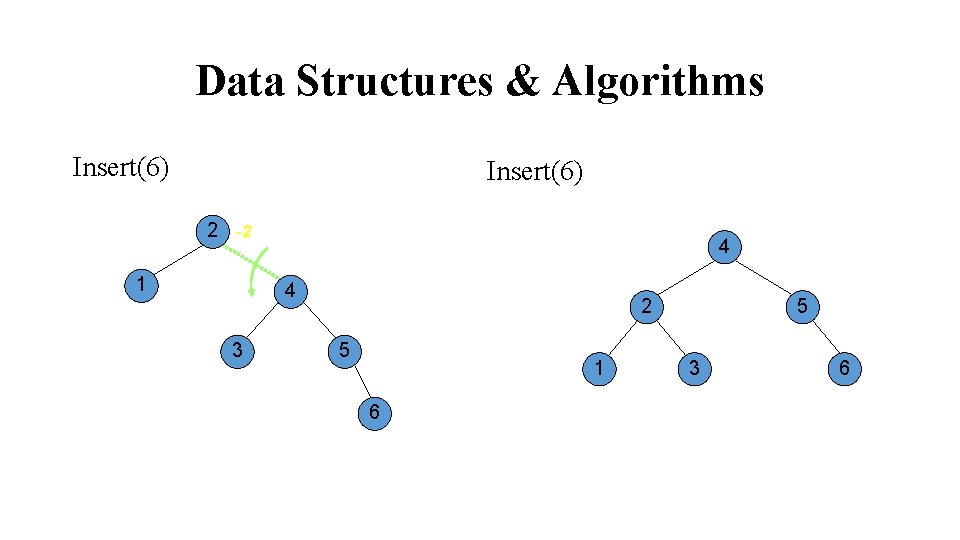
Data Structures & Algorithms Insert(6) 2 -2 1 4 4 3 2 5 1 6 5 3 6

Data Structures & Algorithms Insert(7) 4 2 1 4 5 3 -2 2 6 1 7 6 3 5 7

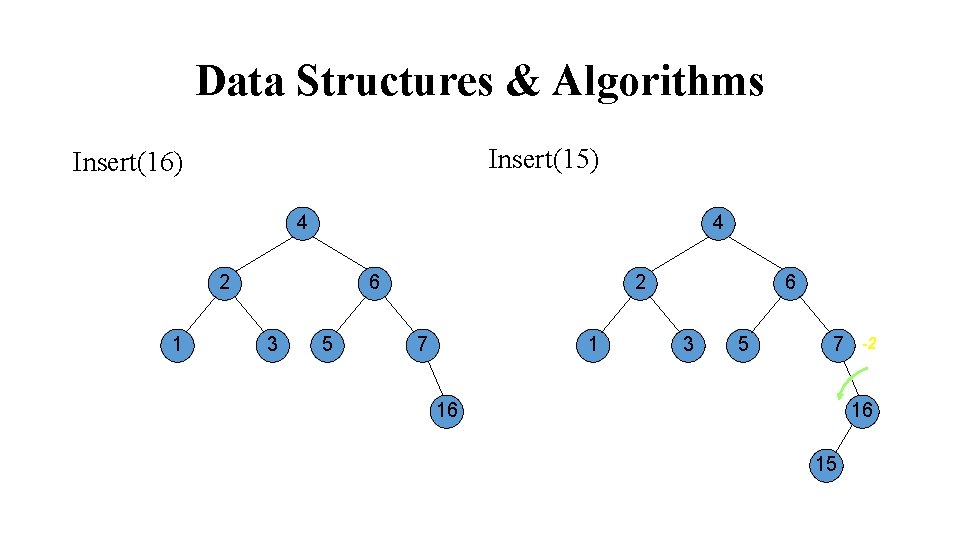
Data Structures & Algorithms Insert(15) Insert(16) 4 4 2 1 6 3 5 2 7 1 6 3 5 7 16 -2 16 15

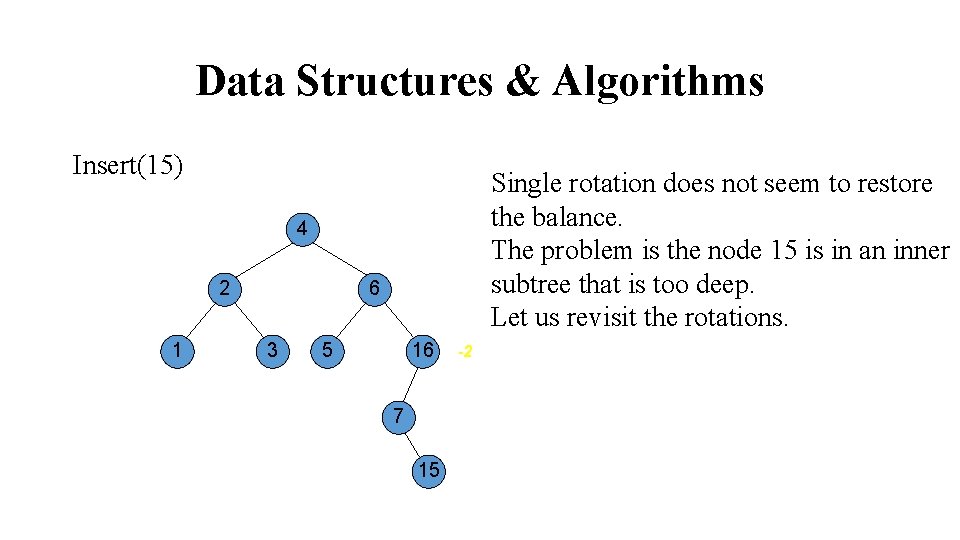
Data Structures & Algorithms Insert(15) Single rotation does not seem to restore the balance. The problem is the node 15 is in an inner subtree that is too deep. Let us revisit the rotations. 4 2 1 6 3 5 16 7 15 -2

Data Structures & Algorithms Let us call the node that must be rebalanced . Since any node has at most two children, and a height imbalance requires that ’s two subtrees differ by two (or – 2), the violation will occur in four cases: 1. An insertion into left subtree of the left child of . 2. An insertion into right subtree of the left child of . 3. An insertion into left subtree of the right child of . 4. An insertion into right subtree of the right child of .

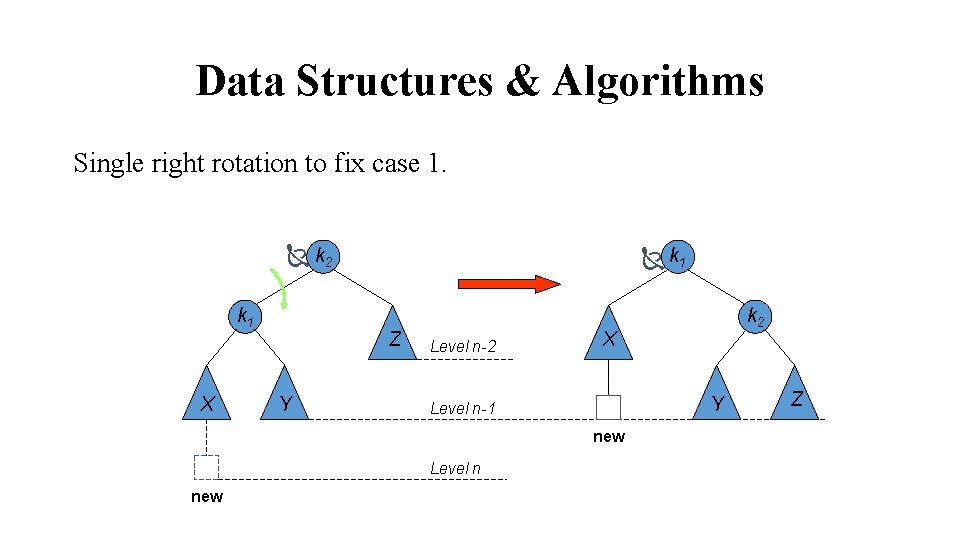
Data Structures & Algorithms The insertion occurs on the “outside” (i. e. , left-left or right-right) in cases 1 and 4 Single rotation can fix the balance in cases 1 and 4. Insertion occurs on the “inside” in cases 2 and 3 which single rotation cannot fix.

Data Structures & Algorithms Single right rotation to fix case 1. k 2 k 1 X k 1 Z Y Level n-2 X Y Level n-1 new Level n new k 2 Z

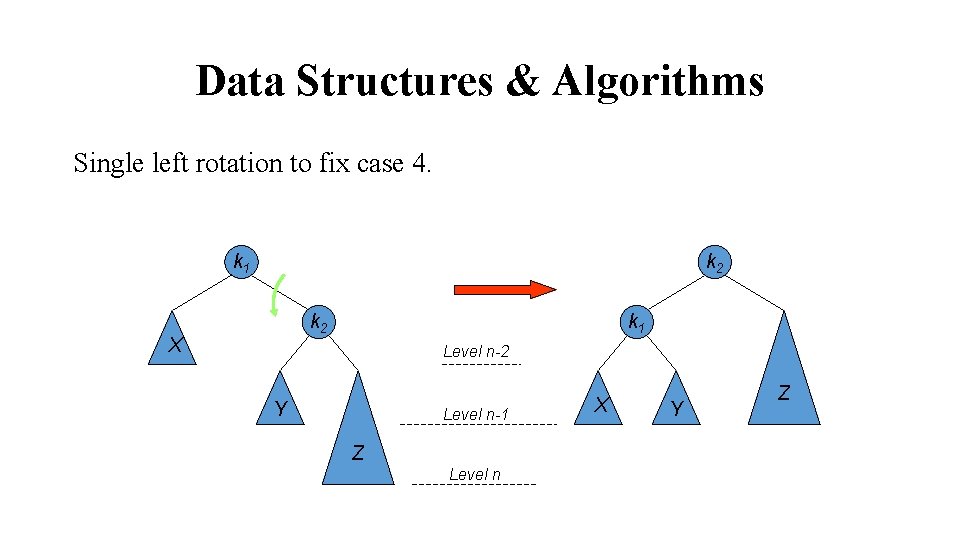
Data Structures & Algorithms Single left rotation to fix case 4. k 1 k 2 X k 1 Level n-2 Y Level n-1 Z Level n X Y Z

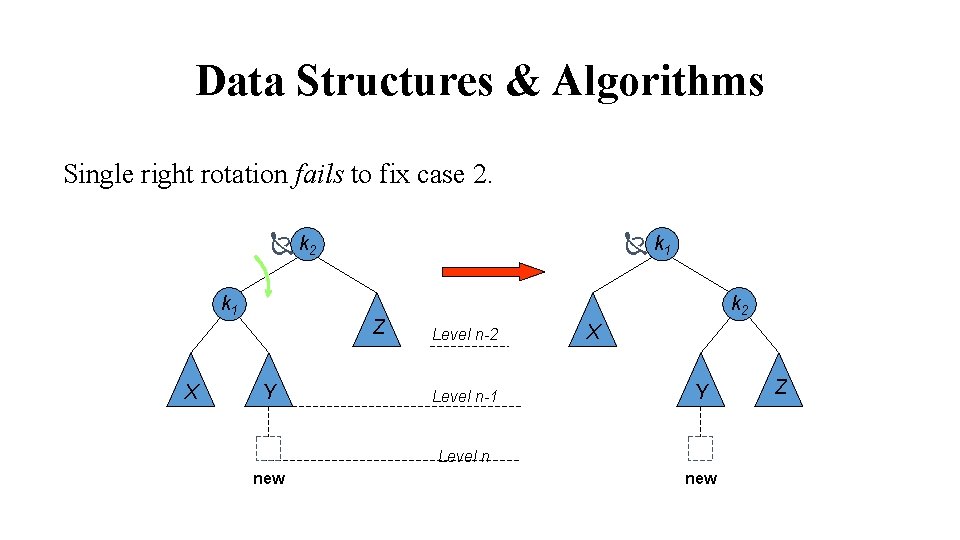
Data Structures & Algorithms Single right rotation fails to fix case 2. k 2 k 1 X k 1 Z Y k 2 Level n-1 X Y Level n new Z

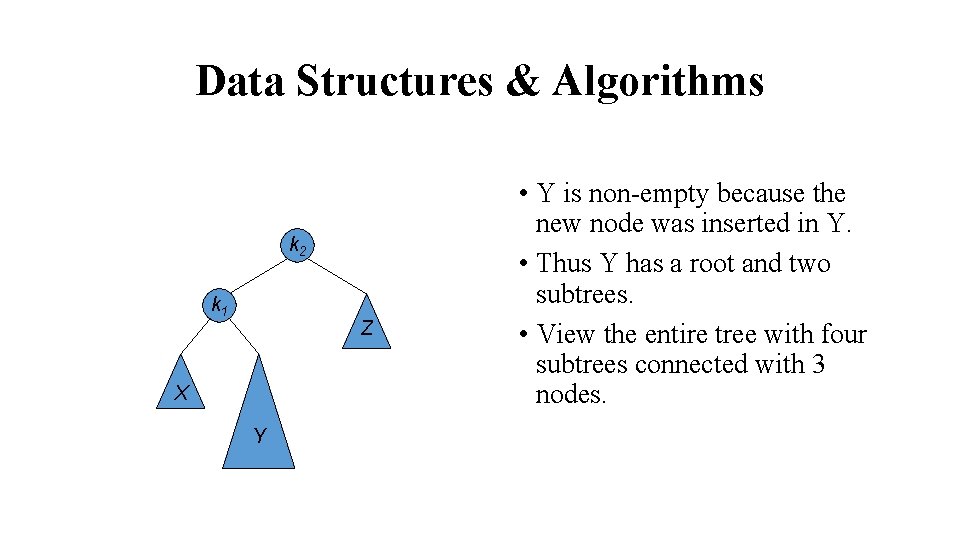
Data Structures & Algorithms k 2 k 1 Z X Y • Y is non-empty because the new node was inserted in Y. • Thus Y has a root and two subtrees. • View the entire tree with four subtrees connected with 3 nodes.

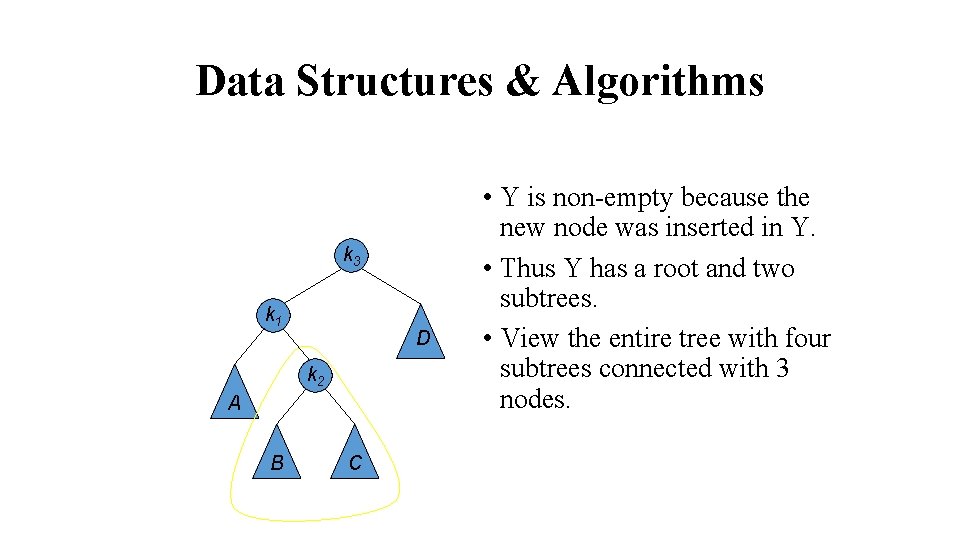
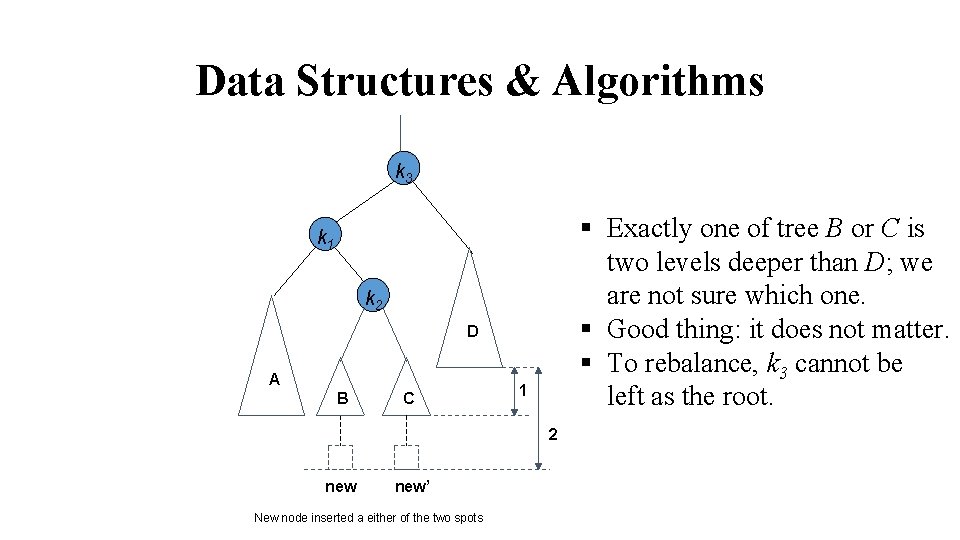
Data Structures & Algorithms k 3 k 1 D k 2 A B C • Y is non-empty because the new node was inserted in Y. • Thus Y has a root and two subtrees. • View the entire tree with four subtrees connected with 3 nodes.

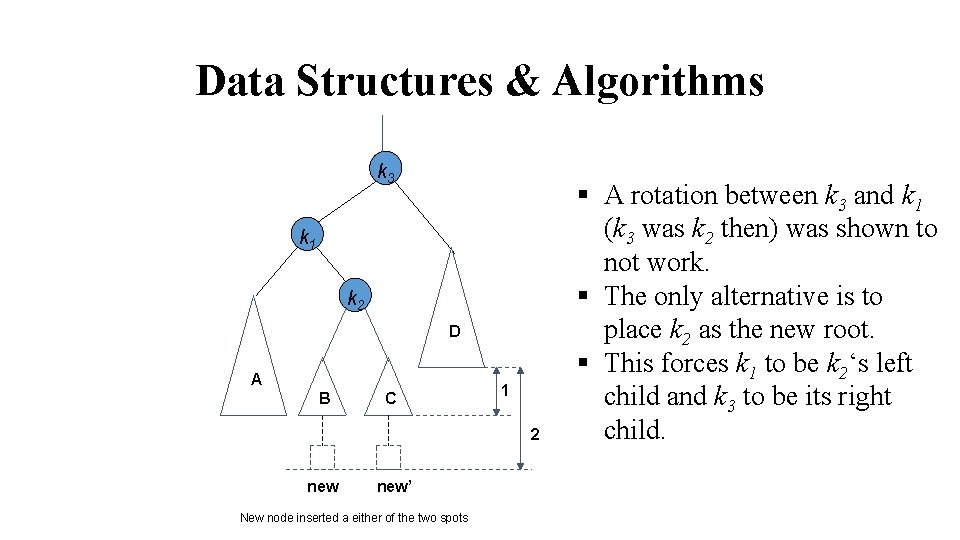
Data Structures & Algorithms k 3 § Exactly one of tree B or C is two levels deeper than D; we are not sure which one. § Good thing: it does not matter. § To rebalance, k 3 cannot be left as the root. k 1 k 2 D A B C 1 2 new’ New node inserted a either of the two spots

Data Structures & Algorithms k 3 k 1 k 2 D A B C 1 2 new’ New node inserted a either of the two spots § A rotation between k 3 and k 1 (k 3 was k 2 then) was shown to not work. § The only alternative is to place k 2 as the new root. § This forces k 1 to be k 2‘s left child and k 3 to be its right child.

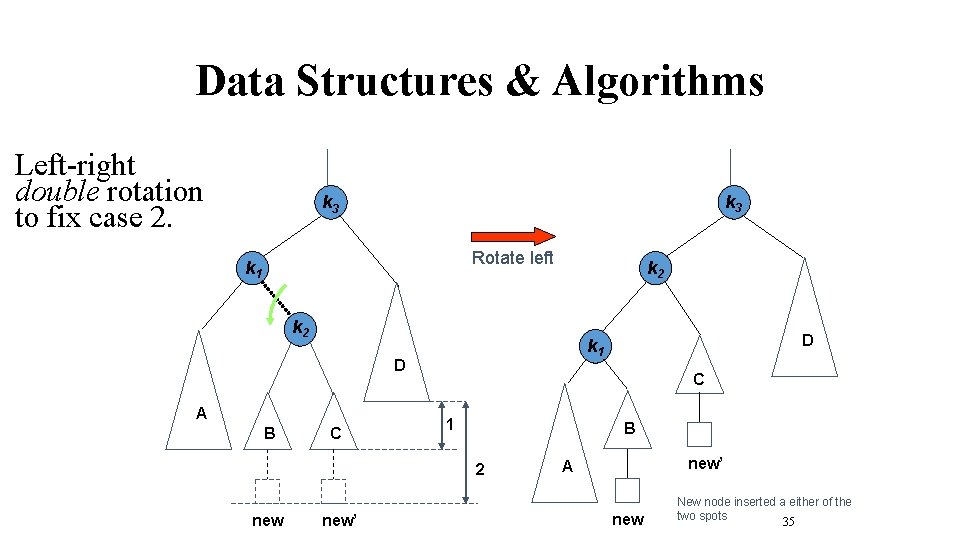
Data Structures & Algorithms Left-right double rotation to fix case 2. k 3 Rotate left k 1 k 2 D A B C C 1 B 2 new’ D k 1 new’ A new New node inserted a either of the two spots 35

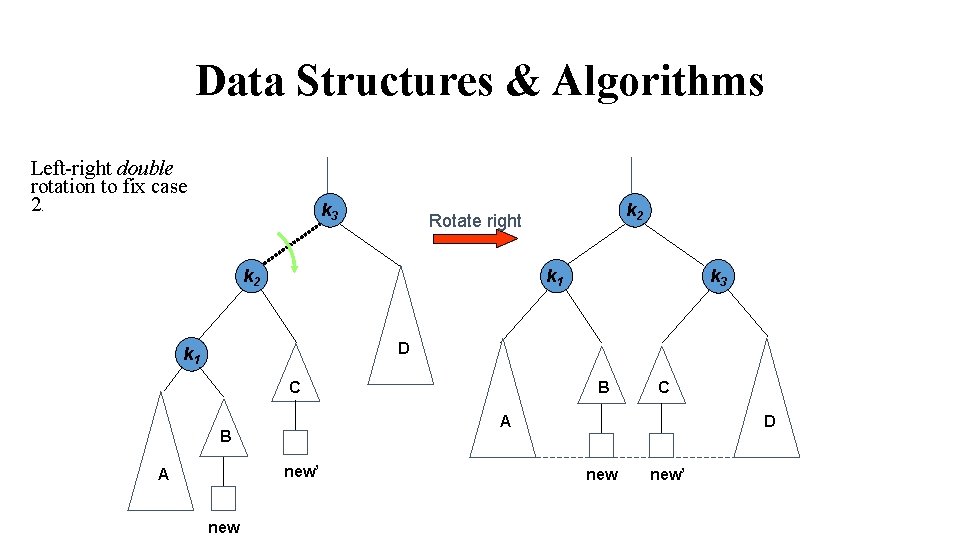
Data Structures & Algorithms Left-right double rotation to fix case 2. k 3 k 2 Rotate right k 2 k 1 k 3 D k 1 C new’ new C A B D new’

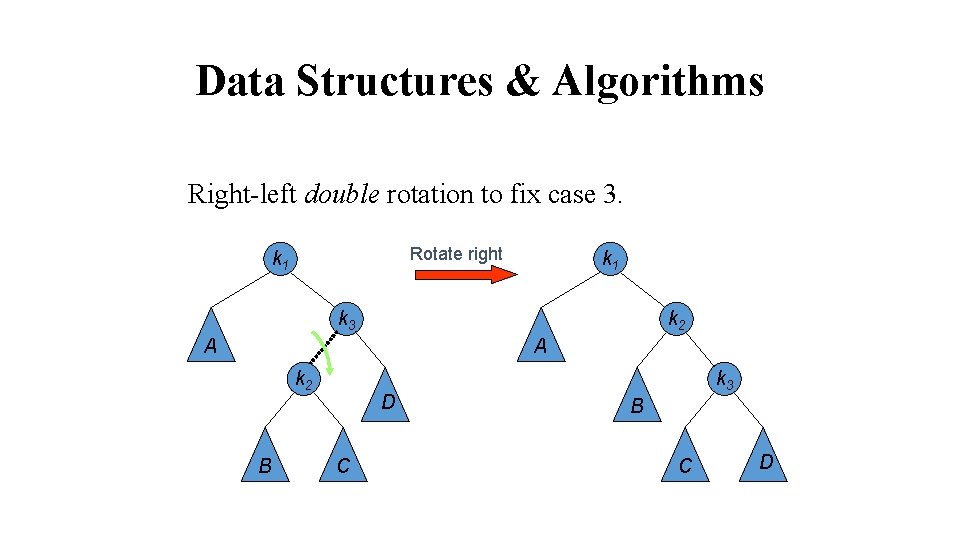
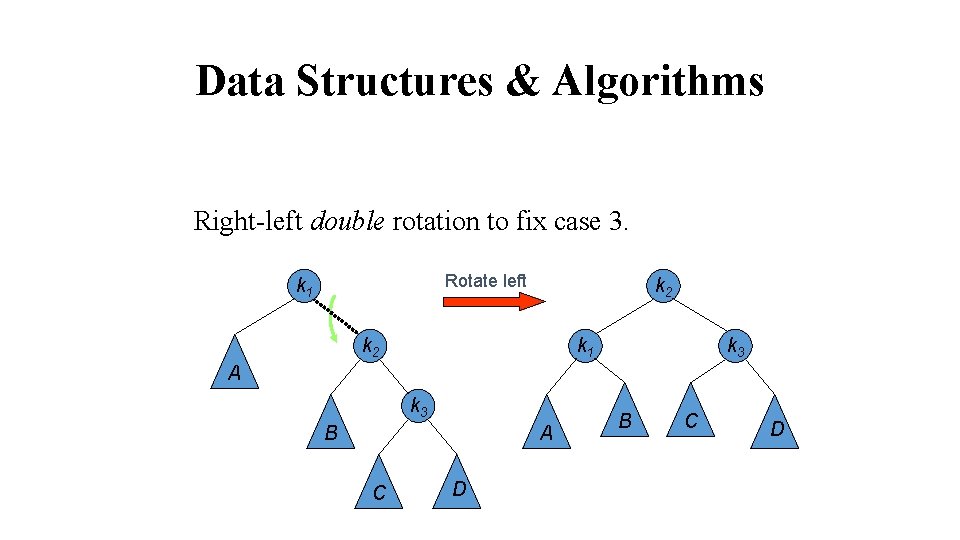
Data Structures & Algorithms Right-left double rotation to fix case 3. Rotate right k 1 k 3 k 2 A A k 2 B D C k 3 B C D

Data Structures & Algorithms Right-left double rotation to fix case 3. Rotate left k 1 k 2 k 1 k 3 A k 3 B A C D B C D

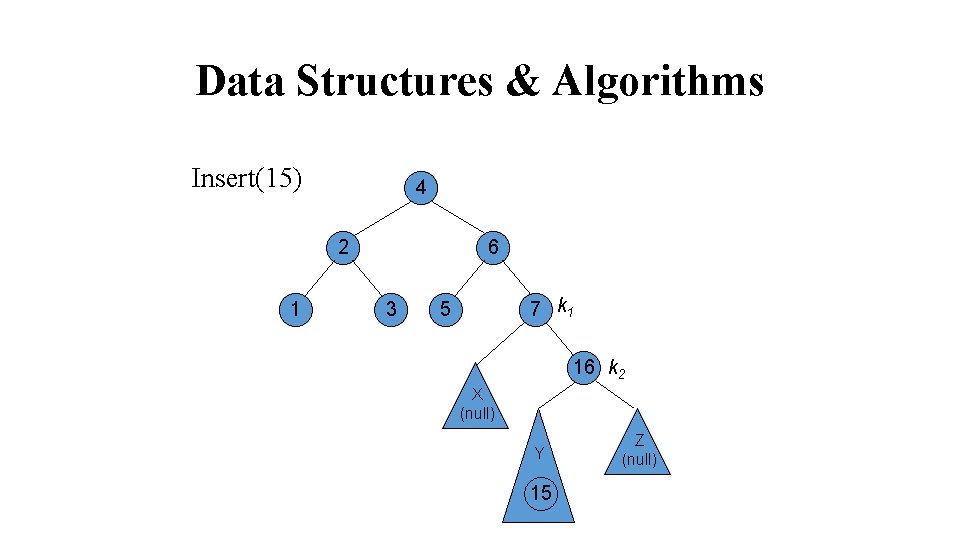
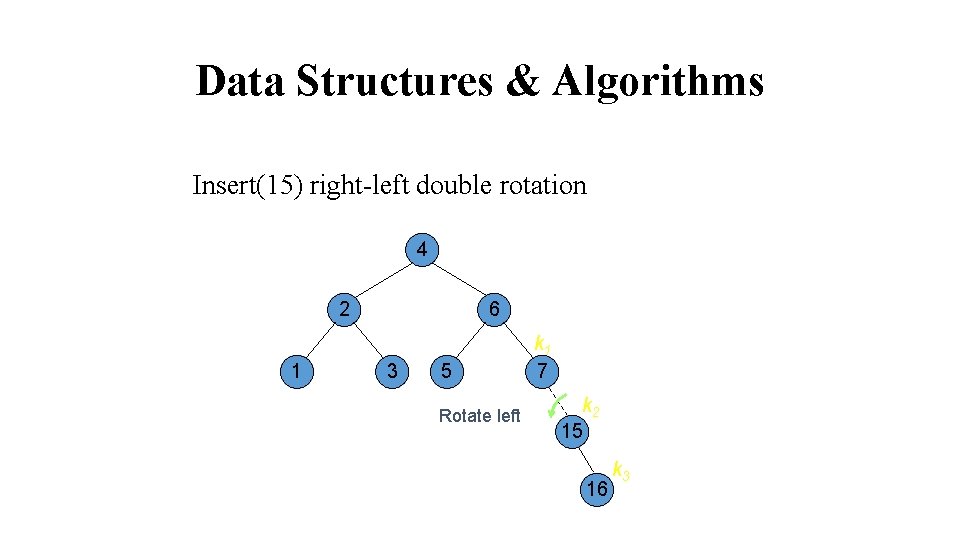
Data Structures & Algorithms Insert(15) 4 2 1 6 3 7 k 1 5 16 k 2 X (null) Y 15 Z (null)

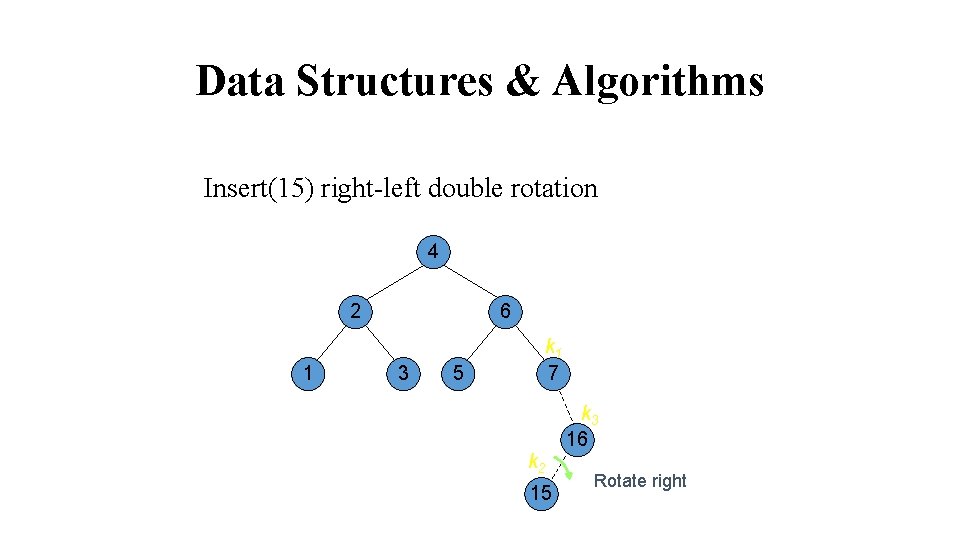
Data Structures & Algorithms Insert(15) right-left double rotation 4 2 1 6 3 5 k 1 7 k 2 15 k 3 16 Rotate right

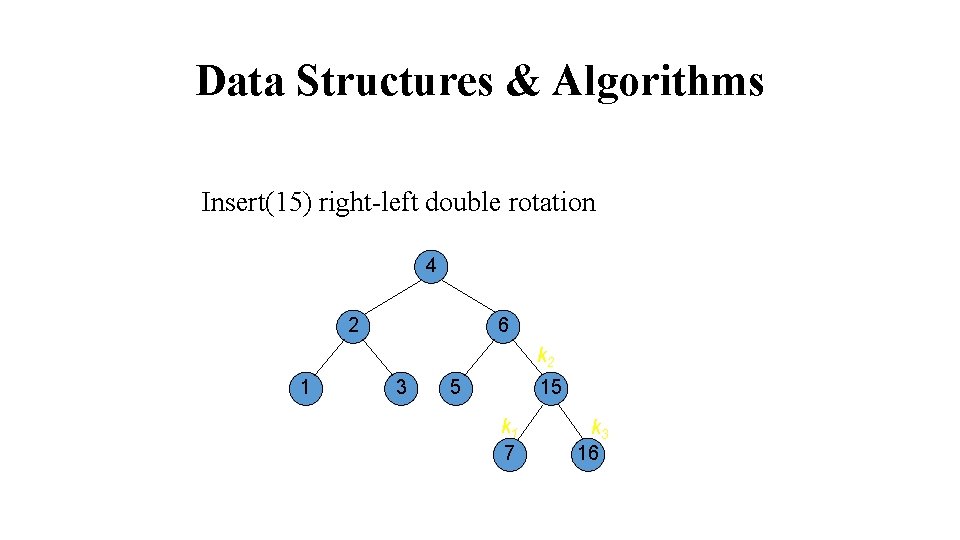
Data Structures & Algorithms Insert(15) right-left double rotation 4 2 1 6 3 5 Rotate left k 1 7 k 2 15 16 k 3

Data Structures & Algorithms Insert(15) right-left double rotation 4 2 6 k 2 1 3 5 15 k 1 7 k 3 16

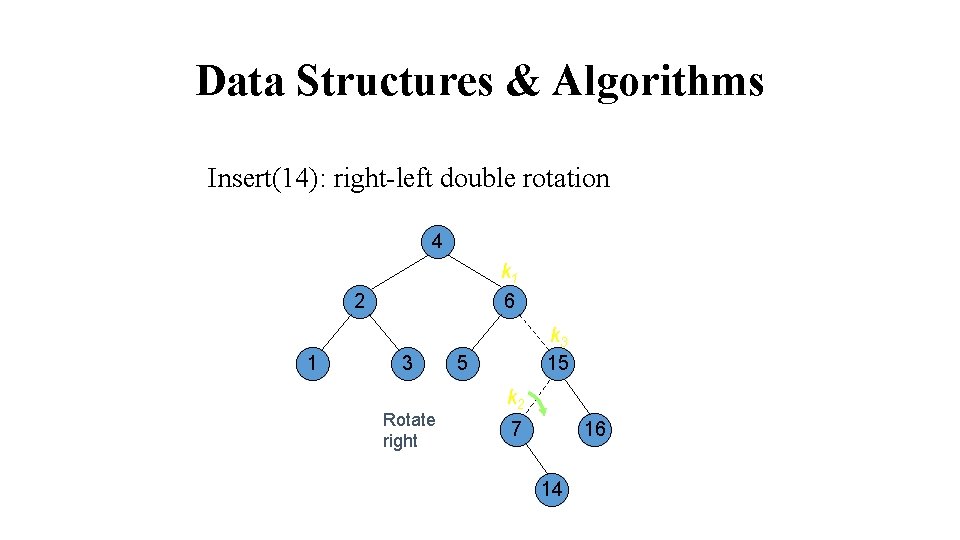
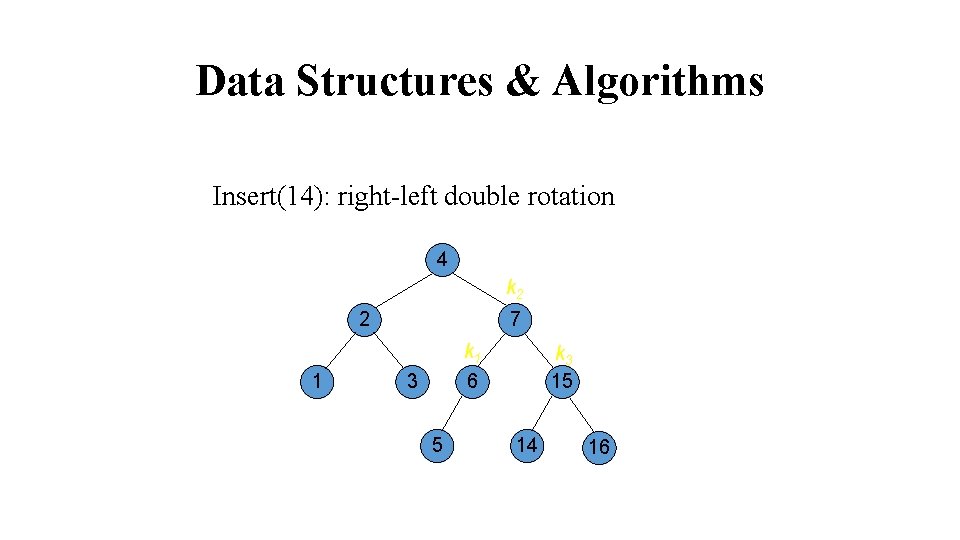
Data Structures & Algorithms Insert(14): right-left double rotation 4 k 1 6 2 1 3 Rotate right k 3 15 5 k 2 7 16 14

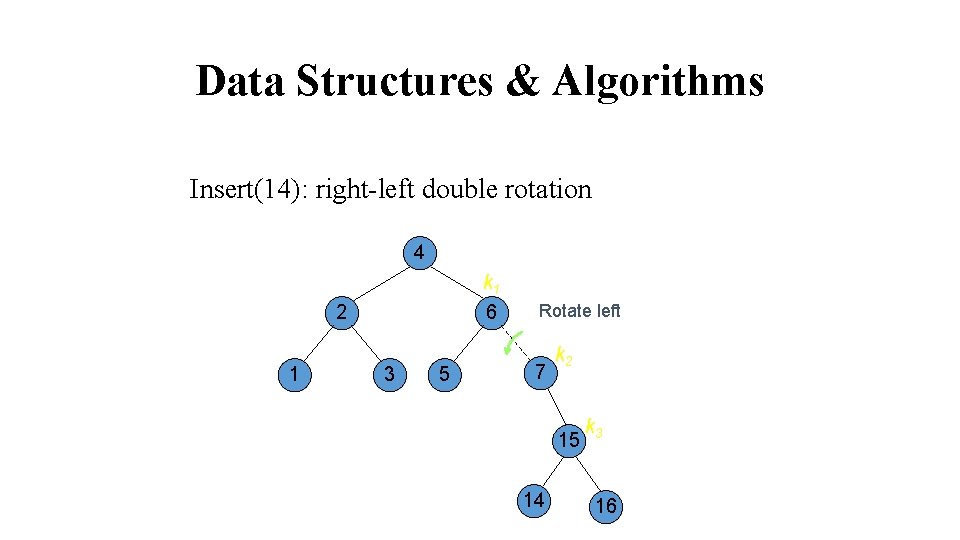
Data Structures & Algorithms Insert(14): right-left double rotation 4 k 1 6 2 1 3 5 Rotate left 7 k 2 15 14 k 3 16

Data Structures & Algorithms Insert(14): right-left double rotation 4 k 2 2 1 7 k 1 6 3 5 k 3 15 14 16

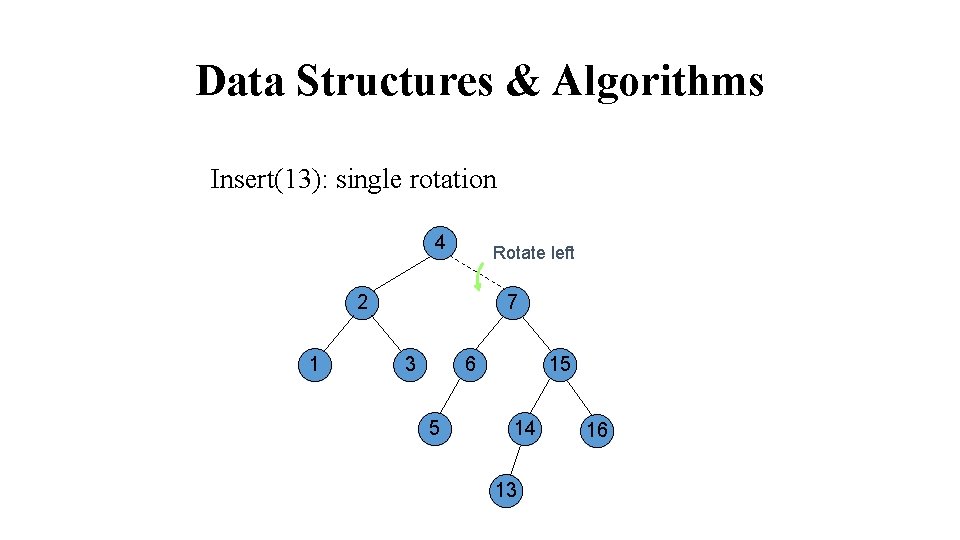
Data Structures & Algorithms Insert(13): single rotation 4 Rotate left 2 1 7 3 6 5 15 14 13 16

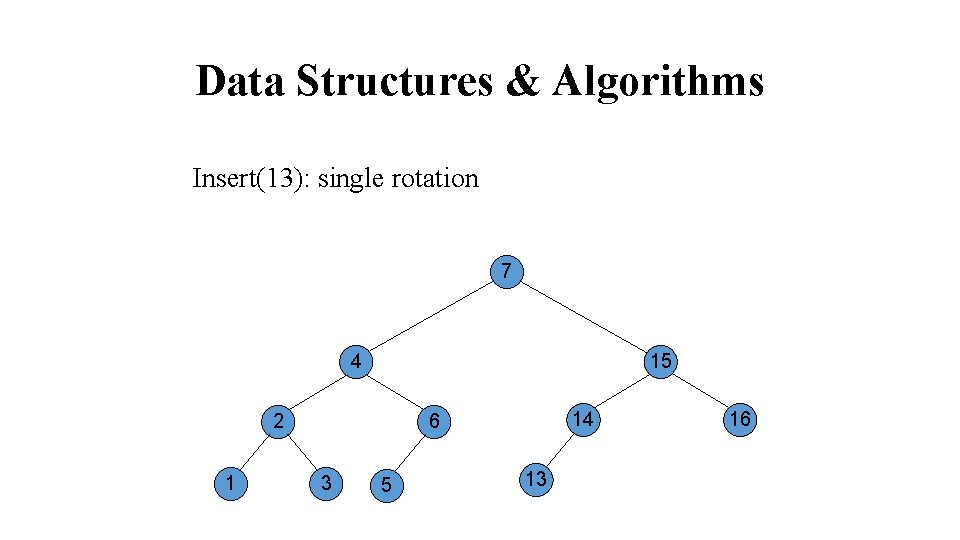
Data Structures & Algorithms Insert(13): single rotation 7 4 15 2 1 14 6 3 5 13 16

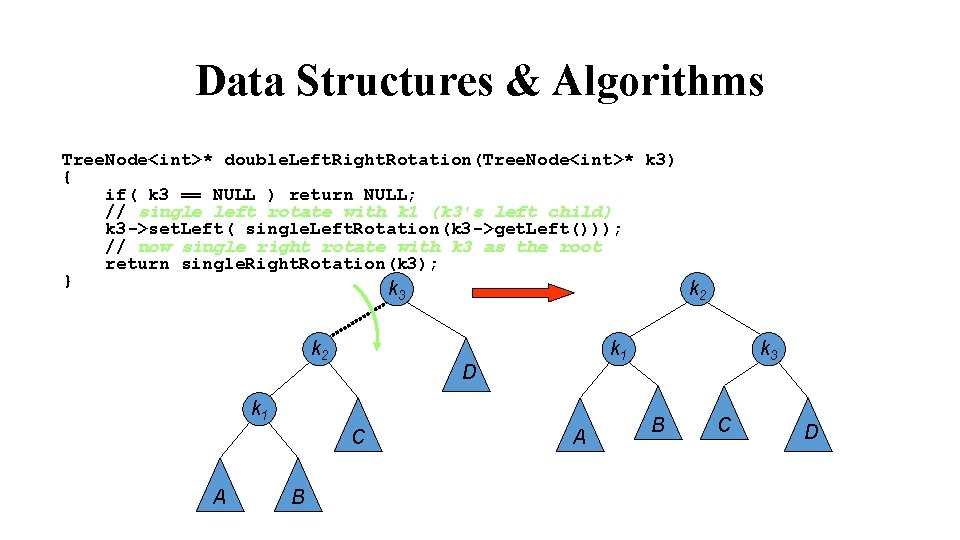
Data Structures & Algorithms Tree. Node<int>* avl. Insert(Tree. Node<int>* root, int info) { Root of left subtree may change if( info < root->get. Info() ){ root->set. Left(avl. Insert(root->get. Left(), info)); int htdiff = height(root->get. Left()) – height(root->get. Right()); if( htdiff == 2 ) if( info < root->get. Left()->get. Info() ) root = single. Right. Rotation( root ); else root = double. Left. Right. Rotation( root ); }

Data Structures & Algorithms Tree. Node<int>* avl. Insert(Tree. Node<int>* root, int info) { if( info < root->get. Info() ){ root->set. Left(avl. Insert(root->get. Left(), info)); int htdiff = height(root->get. Left()) – height(root->get. Right()); if( htdiff == 2 ) if( info < root->get. Left()->get. Info() ) root = single. Right. Rotation( root ); else Outside case root = double. Left. Right. Rotation( root ); } inside case

Data Structures & Algorithms else if(info > root->get. Info() ) { root->set. Right(avl. Insert(root>get. Right(), info)); int htdiff = height(root->get. Right()) – height(root->get. Left()); if( htdiff == 2 ) if( info > root->get. Right()->get. Info() ) root = single. Left. Rotation( root ); else root = double. Right. Left. Rotation( root ); } // else a node with info is already in the tree. In // case, reset the height of this root node. int ht = Max(height(root->get. Left()), height(root->get. Right())); root->set. Height( ht+1 ); // new height for root. return root; }

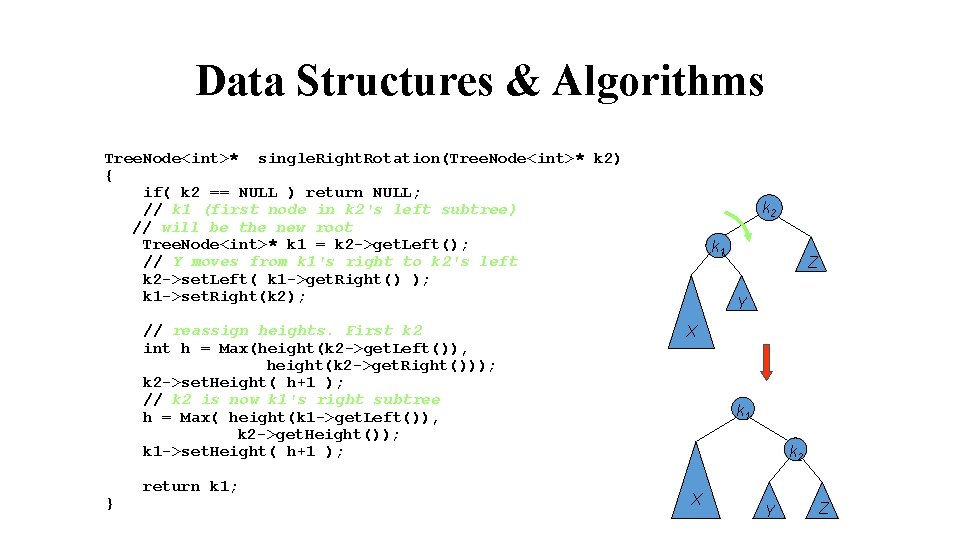
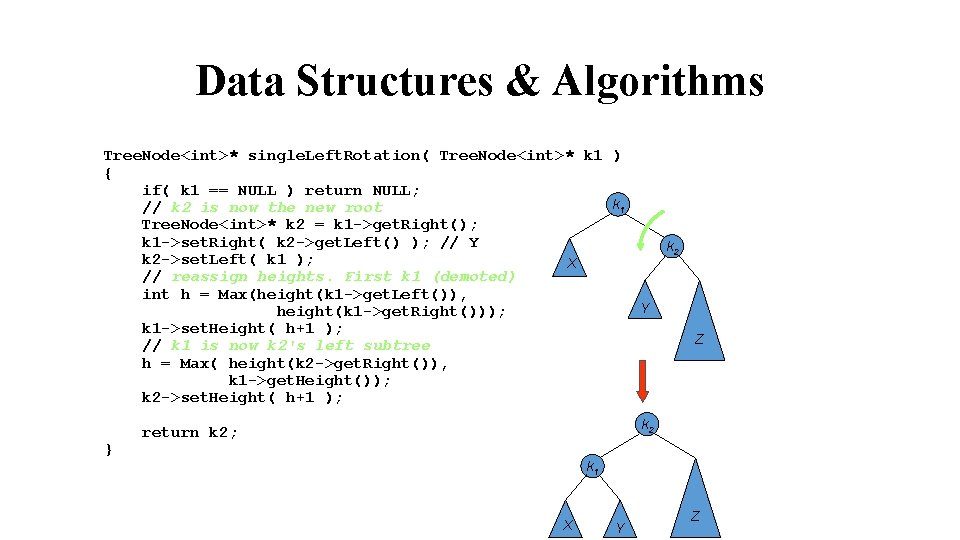
Data Structures & Algorithms Tree. Node<int>* single. Right. Rotation(Tree. Node<int>* k 2) { if( k 2 == NULL ) return NULL; // k 1 (first node in k 2's left subtree) // will be the new root Tree. Node<int>* k 1 = k 2 ->get. Left(); // Y moves from k 1's right to k 2's left k 2 ->set. Left( k 1 ->get. Right() ); k 1 ->set. Right(k 2); // reassign heights. First k 2 int h = Max(height(k 2 ->get. Left()), height(k 2 ->get. Right())); k 2 ->set. Height( h+1 ); // k 2 is now k 1's right subtree h = Max( height(k 1 ->get. Left()), k 2 ->get. Height()); k 1 ->set. Height( h+1 ); } return k 1; k 2 k 1 Z Y X k 1 k 2 X Y Z

Data Structures & Algorithms int height( Tree. Node<int>* node ) { if( node != NULL ) return node->get. Height(); return -1; }

Data Structures & Algorithms Tree. Node<int>* single. Left. Rotation( Tree. Node<int>* k 1 ) { if( k 1 == NULL ) return NULL; k 1 // k 2 is now the new root Tree. Node<int>* k 2 = k 1 ->get. Right(); k 1 ->set. Right( k 2 ->get. Left() ); // Y k 2 ->set. Left( k 1 ); X // reassign heights. First k 1 (demoted) int h = Max(height(k 1 ->get. Left()), height(k 1 ->get. Right())); k 1 ->set. Height( h+1 ); // k 1 is now k 2's left subtree h = Max( height(k 2 ->get. Right()), k 1 ->get. Height()); k 2 ->set. Height( h+1 ); } k 2 Y Z k 2 return k 2; k 1 X Y Z

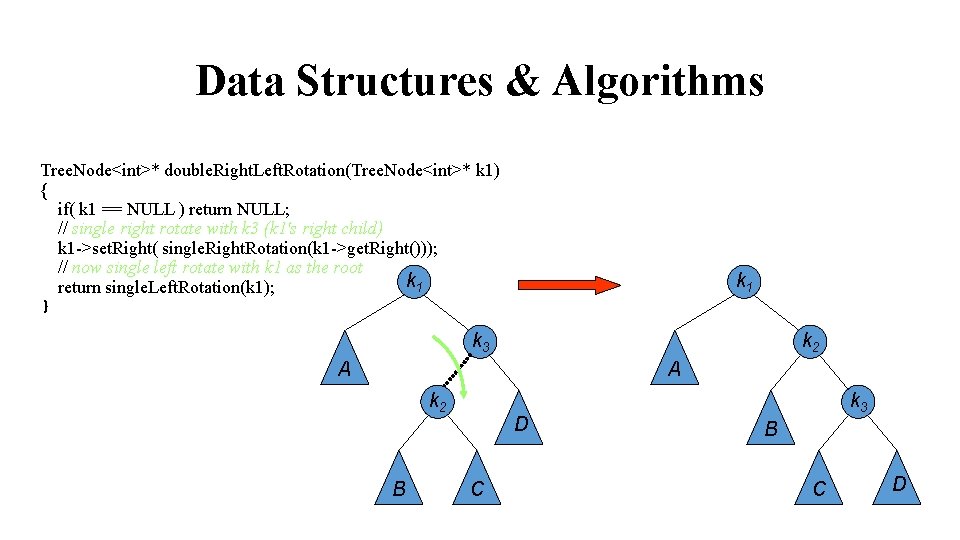
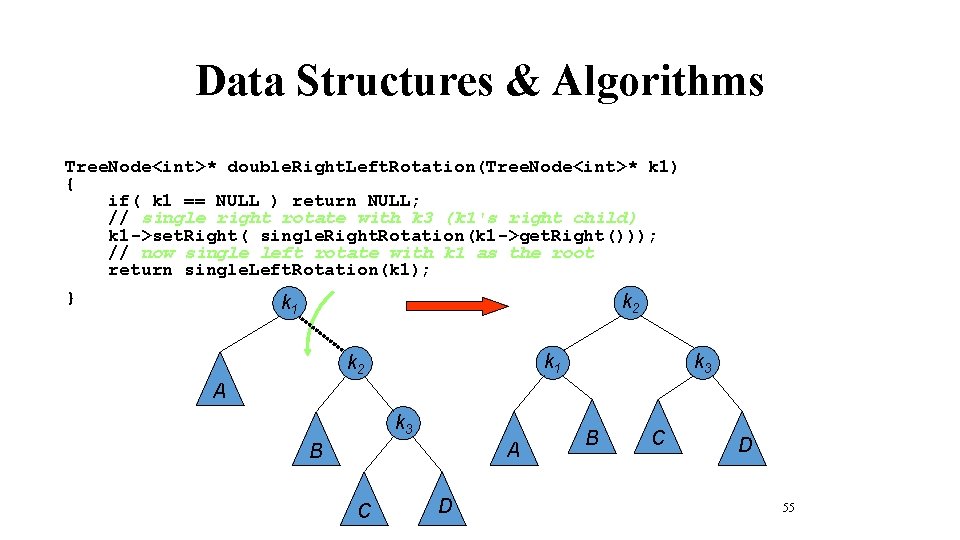
Data Structures & Algorithms Tree. Node<int>* double. Right. Left. Rotation(Tree. Node<int>* k 1) { if( k 1 == NULL ) return NULL; // single right rotate with k 3 (k 1's right child) k 1 ->set. Right( single. Right. Rotation(k 1 ->get. Right())); // now single left rotate with k 1 as the root k 1 return single. Left. Rotation(k 1); } k 1 k 3 k 2 A A k 2 B D C k 3 B C 54 D

Data Structures & Algorithms Tree. Node<int>* double. Right. Left. Rotation(Tree. Node<int>* k 1) { if( k 1 == NULL ) return NULL; // single right rotate with k 3 (k 1's right child) k 1 ->set. Right( single. Right. Rotation(k 1 ->get. Right())); // now single left rotate with k 1 as the root return single. Left. Rotation(k 1); } k 2 k 1 k 2 k 3 A B C D 55

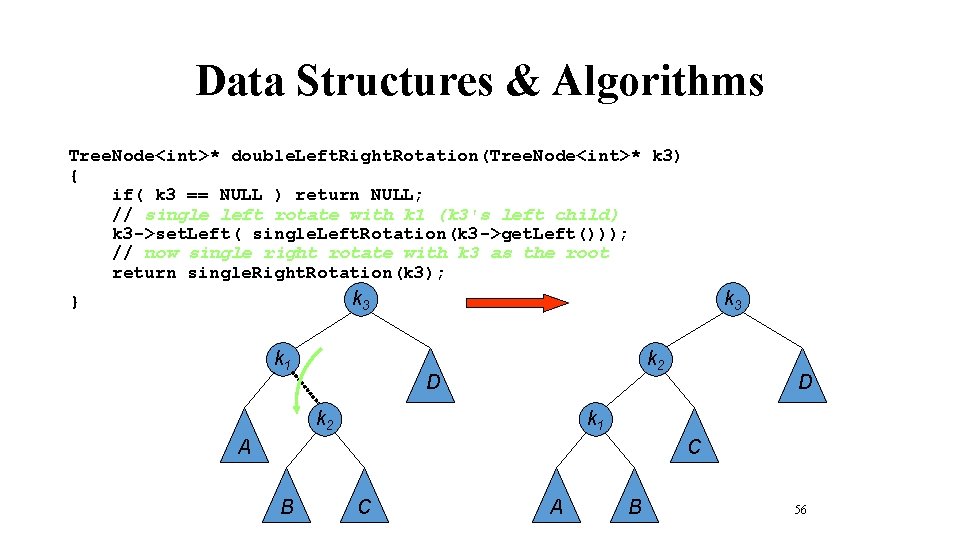
Data Structures & Algorithms Tree. Node<int>* double. Left. Right. Rotation(Tree. Node<int>* k 3) { if( k 3 == NULL ) return NULL; // single left rotate with k 1 (k 3's left child) k 3 ->set. Left( single. Left. Rotation(k 3 ->get. Left())); // now single right rotate with k 3 as the root return single. Right. Rotation(k 3); k 3 } k 1 k 3 k 2 D k 1 A C B C A B 56

Data Structures & Algorithms Tree. Node<int>* double. Left. Right. Rotation(Tree. Node<int>* k 3) { if( k 3 == NULL ) return NULL; // single left rotate with k 1 (k 3's left child) k 3 ->set. Left( single. Left. Rotation(k 3 ->get. Left())); // now single right rotate with k 3 as the root return single. Right. Rotation(k 3); } k 3 k 2 k 1 D k 1 C A B A k 3 B C D

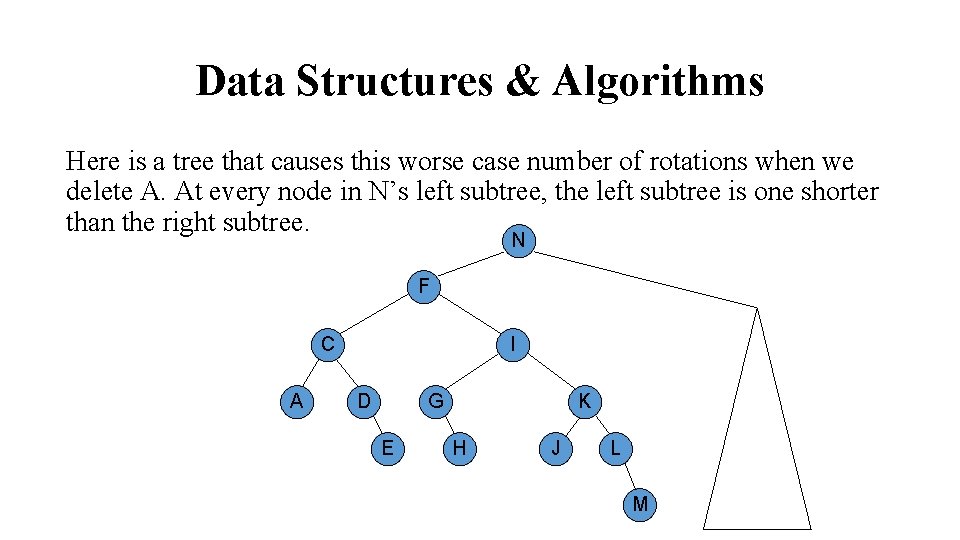
Data Structures & Algorithms Deletion in AVL Tree: Delete is the inverse of insert: given a value X and an AVL tree T, delete the node containing X and rebalance the tree, if necessary. Turns out that deletion of a node is considerably more complex than insert. Insertion in a height-balanced tree requires at most one single rotation or one double rotation. We can use rotations to restore the balance when we do a deletion. We may have to do a rotation at every level of the tree: log 2 N rotations in the worst case.

Data Structures & Algorithms Here is a tree that causes this worse case number of rotations when we delete A. At every node in N’s left subtree, the left subtree is one shorter than the right subtree. N F C A I D G E K H J L M

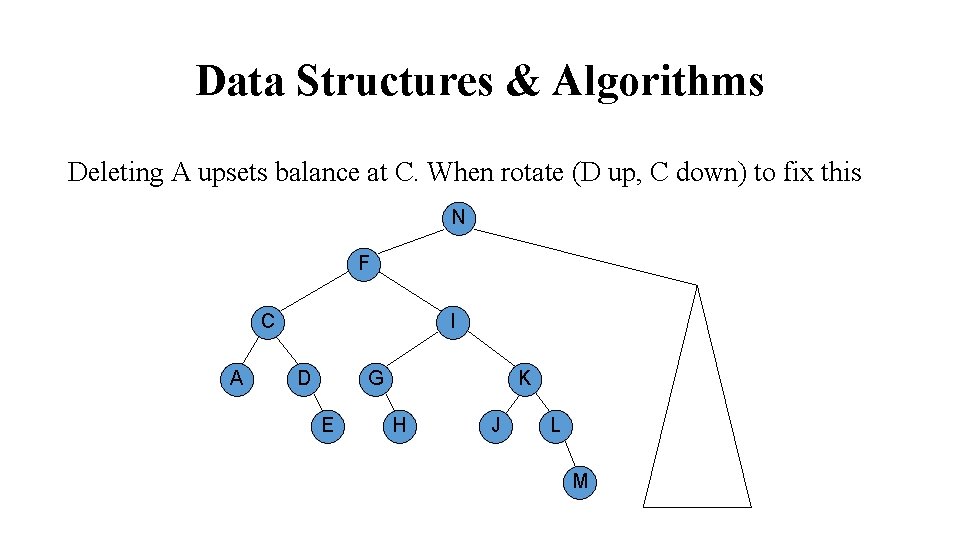
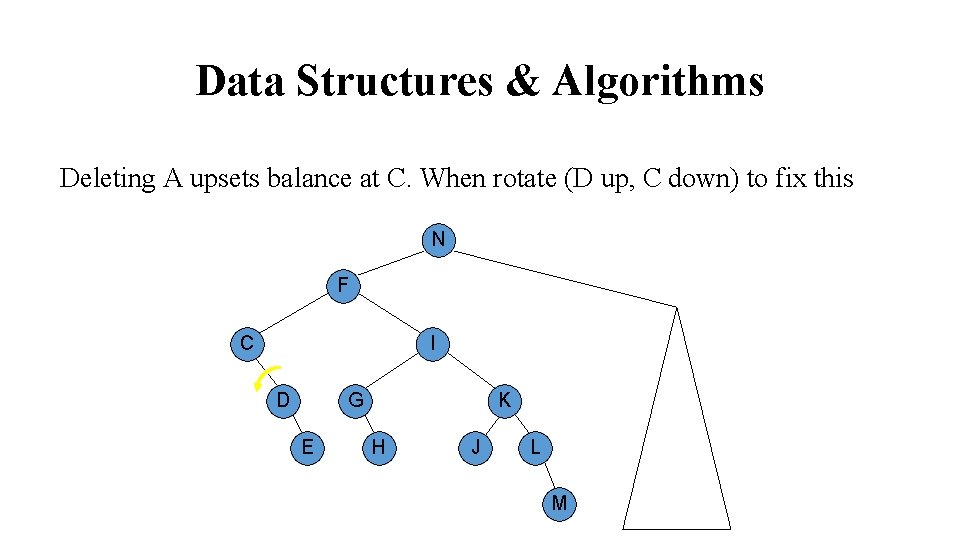
Data Structures & Algorithms Deleting A upsets balance at C. When rotate (D up, C down) to fix this N F C A I D G E K H J L M

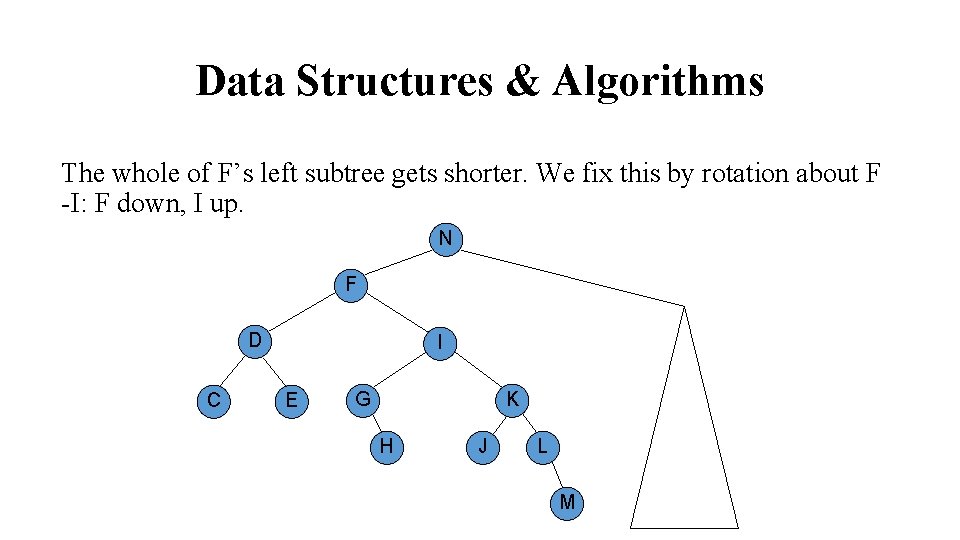
Data Structures & Algorithms Deleting A upsets balance at C. When rotate (D up, C down) to fix this N F C I D G E K H J L M

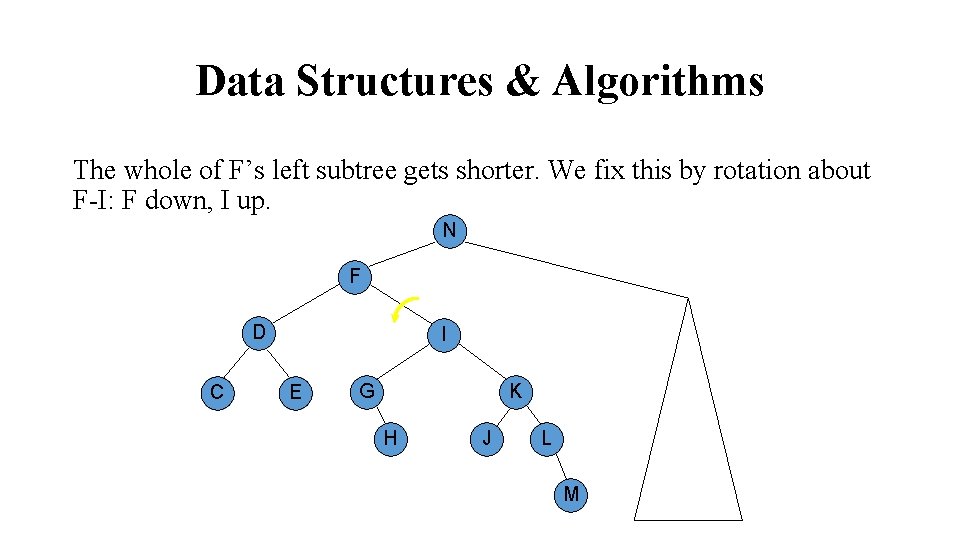
Data Structures & Algorithms The whole of F’s left subtree gets shorter. We fix this by rotation about F -I: F down, I up. N F D C I E G K H J L M

Data Structures & Algorithms The whole of F’s left subtree gets shorter. We fix this by rotation about F-I: F down, I up. N F D C I E G K H J L M

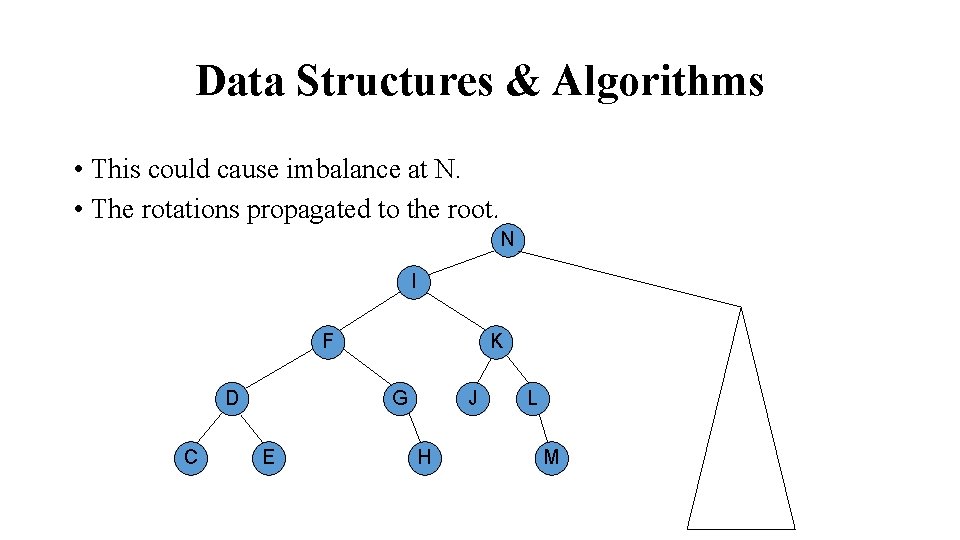
Data Structures & Algorithms • This could cause imbalance at N. • The rotations propagated to the root. N I F D C K G E J H L M

Data Structures & Algorithms Procedure: Delete the node as in binary search tree (BST). The node deleted will be either a leaf or have just one subtree. Since this is an AVL tree, if the deleted node has one subtree, that subtree contains only one node (why? ) Traverse up the tree from the deleted node checking the balance of each node. There are 5 cases to consider. Let us go through the cases graphically and determine what action to take. We will not develop the C++ code for delete. Node in AVL tree. This will be left as an exercise.

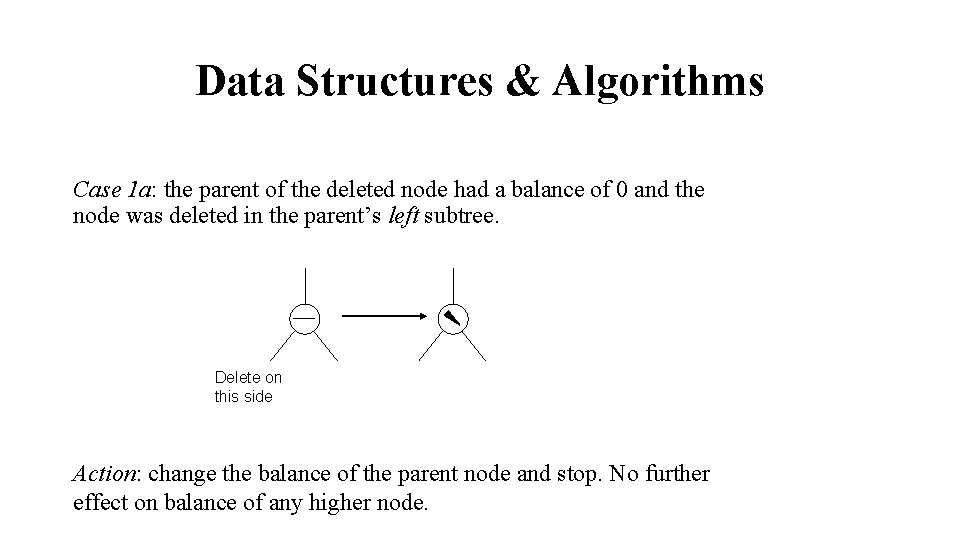
Data Structures & Algorithms Case 1 a: the parent of the deleted node had a balance of 0 and the node was deleted in the parent’s left subtree. Delete on this side Action: change the balance of the parent node and stop. No further effect on balance of any higher node.

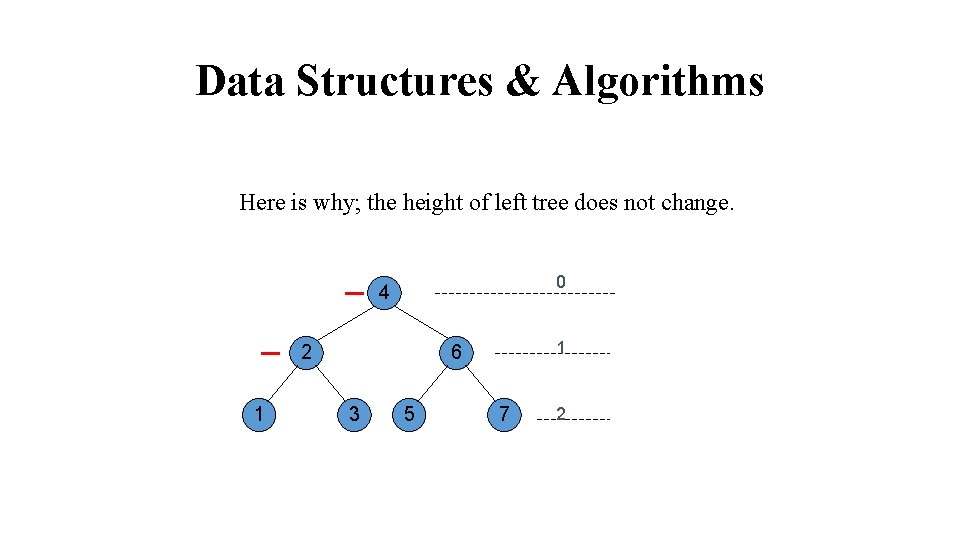
Data Structures & Algorithms Here is why; the height of left tree does not change. 0 4 2 1 1 6 3 5 7 2

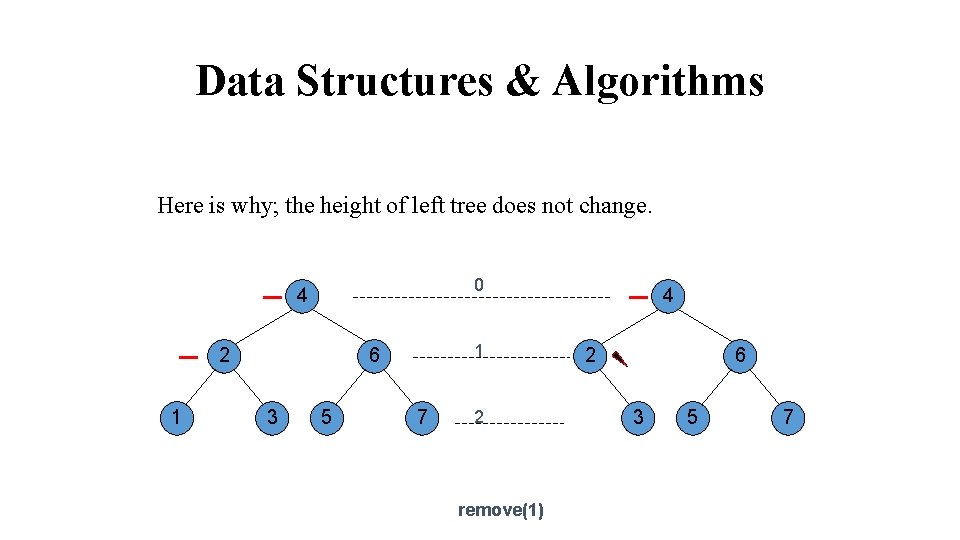
Data Structures & Algorithms Here is why; the height of left tree does not change. 0 4 2 1 1 6 3 5 7 2 remove(1) 4 2 6 3 5 7

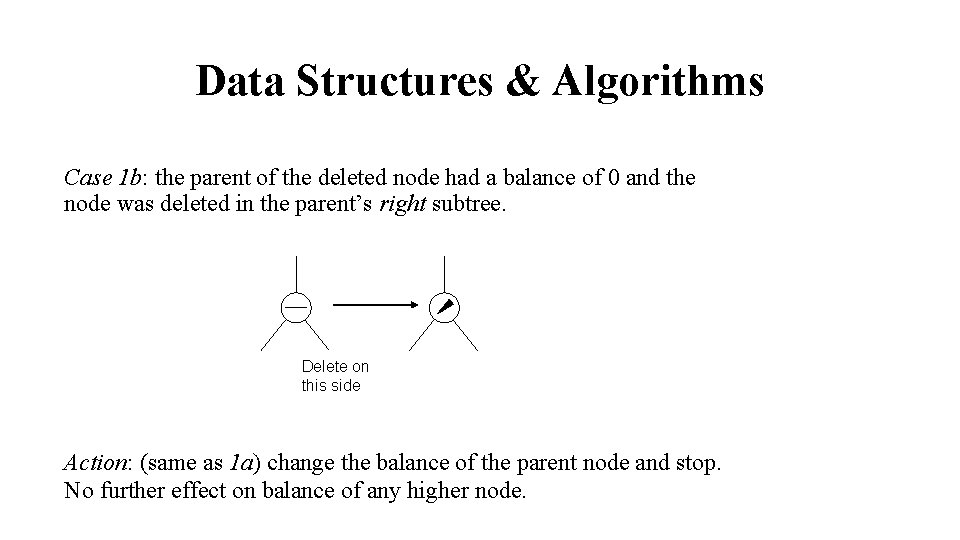
Data Structures & Algorithms Case 1 b: the parent of the deleted node had a balance of 0 and the node was deleted in the parent’s right subtree. Delete on this side Action: (same as 1 a) change the balance of the parent node and stop. No further effect on balance of any higher node.

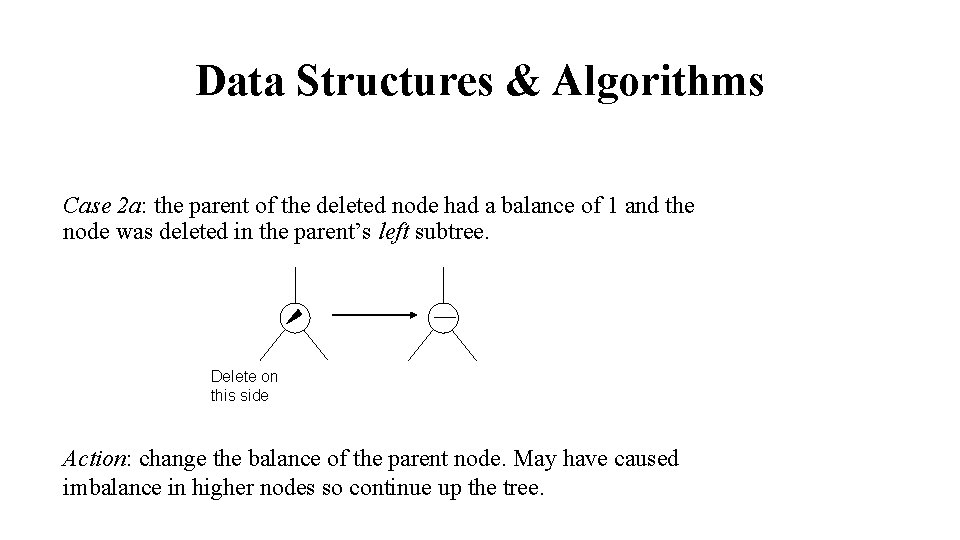
Data Structures & Algorithms Case 2 a: the parent of the deleted node had a balance of 1 and the node was deleted in the parent’s left subtree. Delete on this side Action: change the balance of the parent node. May have caused imbalance in higher nodes so continue up the tree.

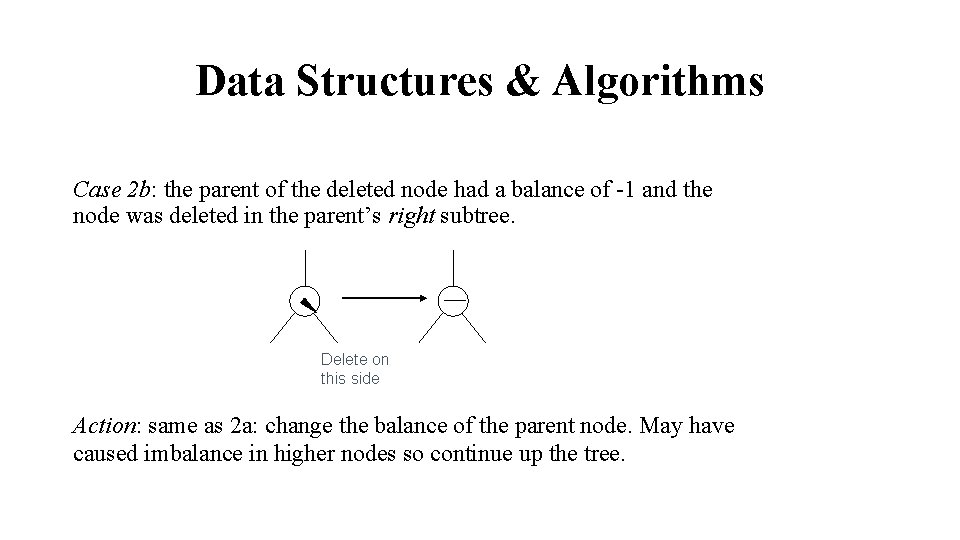
Data Structures & Algorithms Case 2 b: the parent of the deleted node had a balance of -1 and the node was deleted in the parent’s right subtree. Delete on this side Action: same as 2 a: change the balance of the parent node. May have caused imbalance in higher nodes so continue up the tree.

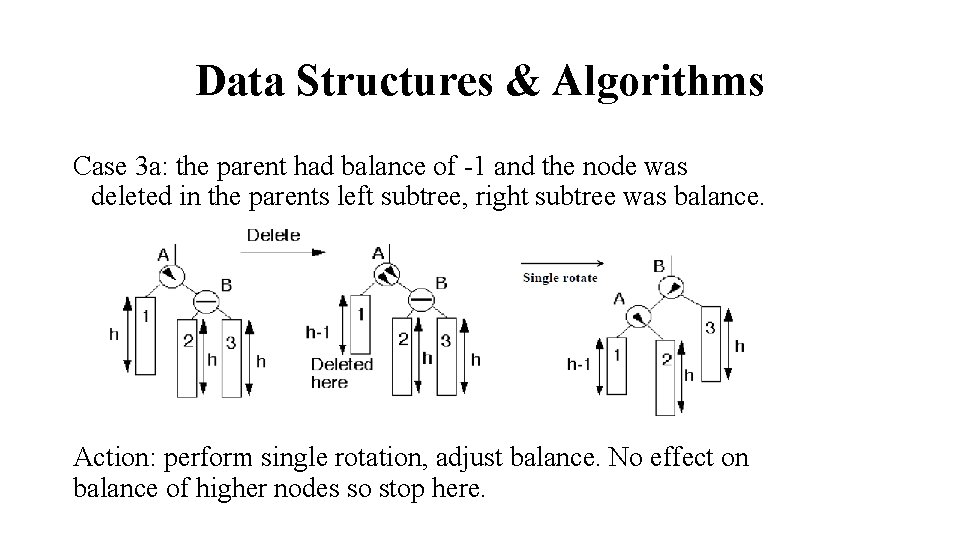
Data Structures & Algorithms Case 3 a: the parent had balance of -1 and the node was deleted in the parents left subtree, right subtree was balance. Action: perform single rotation, adjust balance. No effect on balance of higher nodes so stop here.

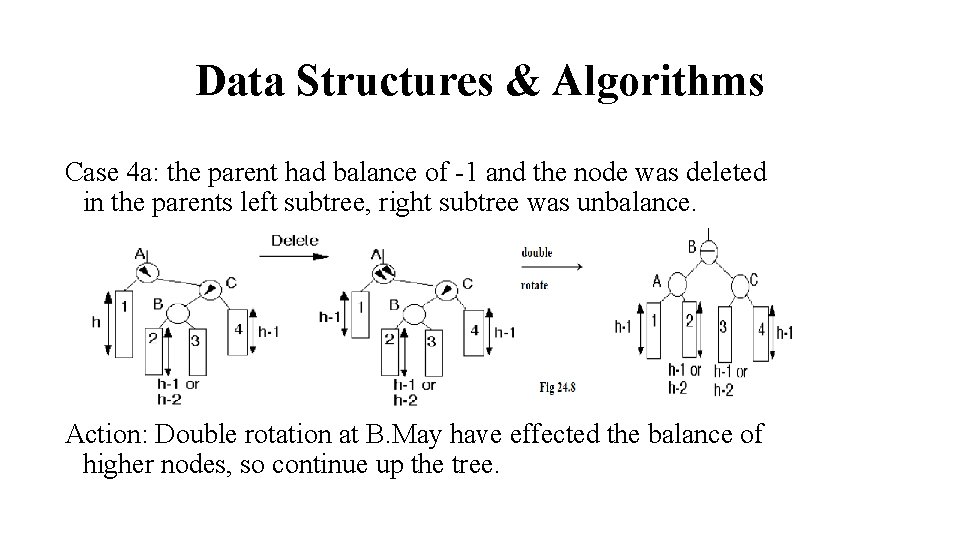
Data Structures & Algorithms Case 4 a: the parent had balance of -1 and the node was deleted in the parents left subtree, right subtree was unbalance. Action: Double rotation at B. May have effected the balance of higher nodes, so continue up the tree.

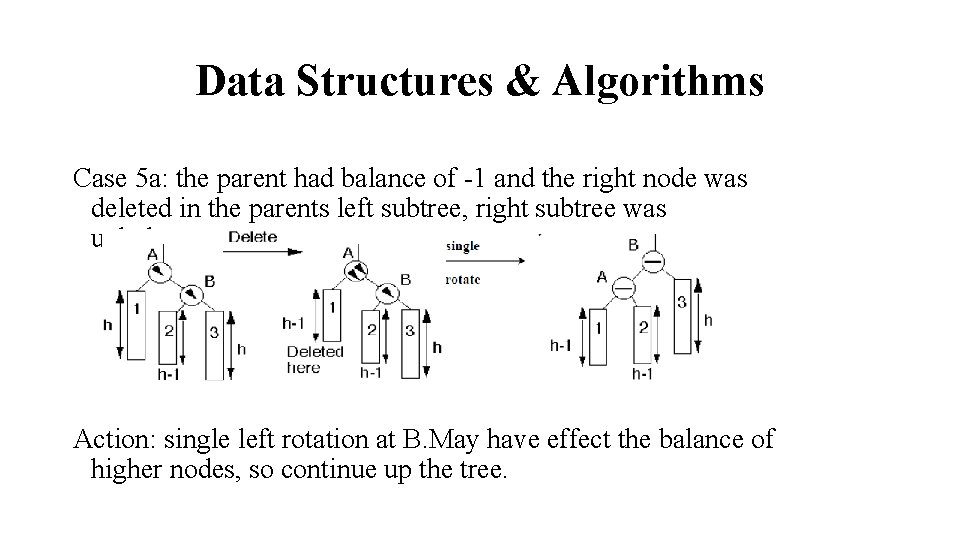
Data Structures & Algorithms Case 5 a: the parent had balance of -1 and the right node was deleted in the parents left subtree, right subtree was unbalance. Action: single left rotation at B. May have effect the balance of higher nodes, so continue up the tree.