The Completely Randomized Design 8 2 Introduction to

The Completely Randomized Design (§ 8. 2) • Introduction to the simplest experimental design - the Completely Randomized Design. • Introduce a statistical model for the observations in a completely randomized design.

Completely Randomized Design Two different Names for the Same Design: • Experimental Study - Completely randomized design (CRD) • Sampling Study - One-way classification design Randomization: The t treatments are randomly allocated to the experimental units in such a way that n 1 units receive treatment 1, n 2 receive treatment 2, etc. Assumptions: • Independent random samples (response from one experimental unit does not affect responses from other experimental units). • Responses follow a normal distribution. • Common true variance, s 2, across all groups/treatments. • True mean for population i is i. • Interest is in comparing means.

AOV Model of Responses/Effects Model: random error ~ N(0, s 2) overall mean effect due to population i Expected response Requirement for to be the overall mean: Estimate All ai = 0 implies all groups have the same mean ( )

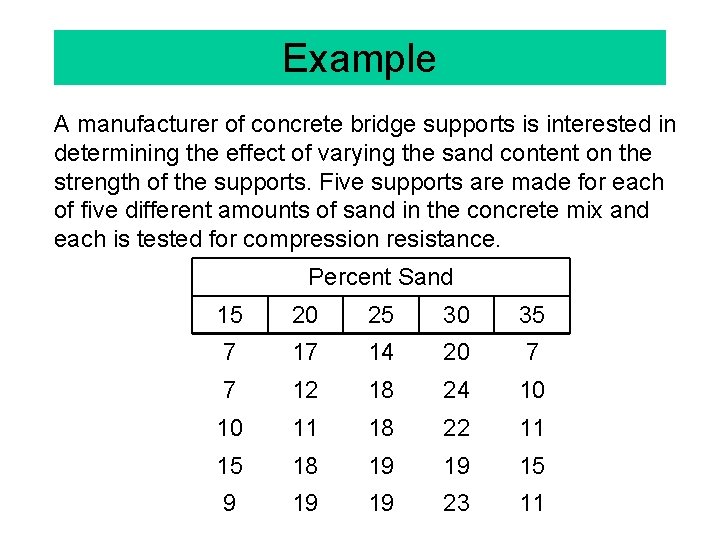
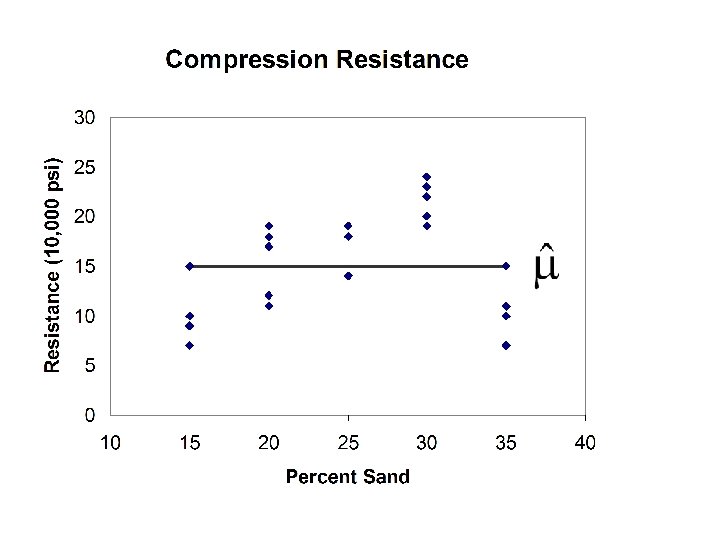
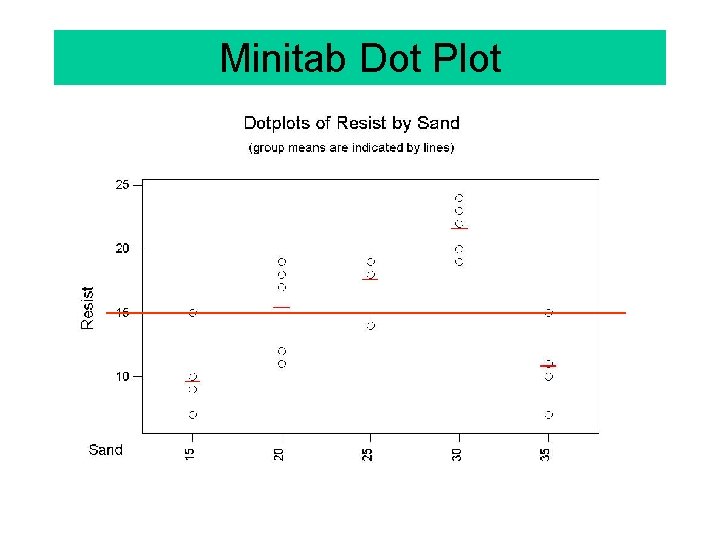
Example A manufacturer of concrete bridge supports is interested in determining the effect of varying the sand content on the strength of the supports. Five supports are made for each of five different amounts of sand in the concrete mix and each is tested for compression resistance. Percent Sand 15 20 25 30 35 7 17 14 20 7 7 12 18 24 10 10 11 18 22 11 15 18 19 19 15 9 19 19 23 11

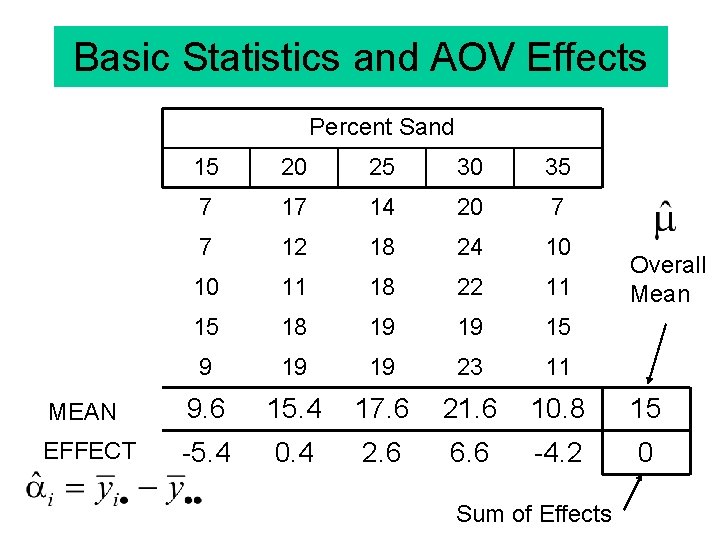
Basic Statistics and AOV Effects Percent Sand 15 20 25 30 35 7 17 14 20 7 7 12 18 24 10 10 11 18 22 11 15 18 19 19 15 9 19 19 23 11 MEAN 9. 6 15. 4 17. 6 21. 6 10. 8 15 EFFECT -5. 4 0. 4 2. 6 6. 6 -4. 2 0 Sum of Effects Overall Mean

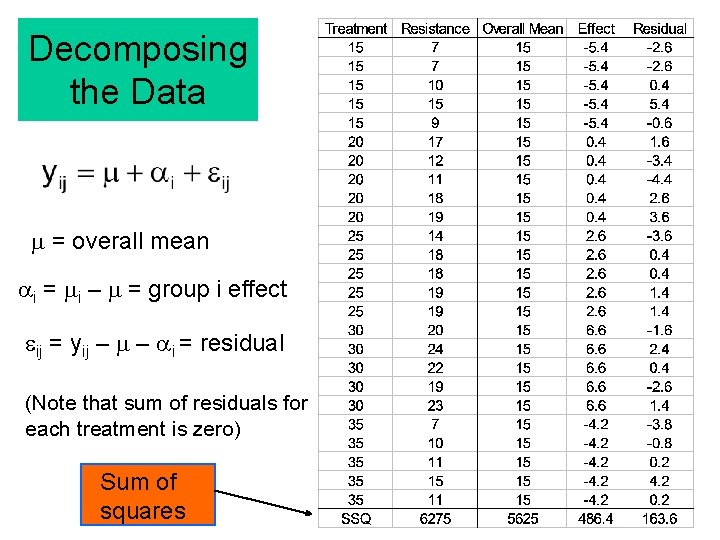
Decomposing the Data = overall mean ai = i – = group i effect ij = yij – – ai = residual (Note that sum of residuals for each treatment is zero) Sum of squares

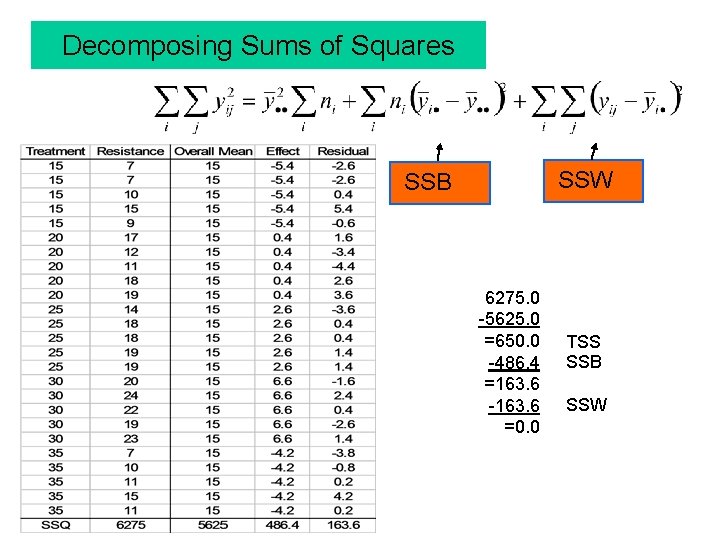
Decomposing Sums of Squares SSW SSB 6275. 0 -5625. 0 =650. 0 -486. 4 =163. 6 -163. 6 =0. 0 TSS SSB SSW

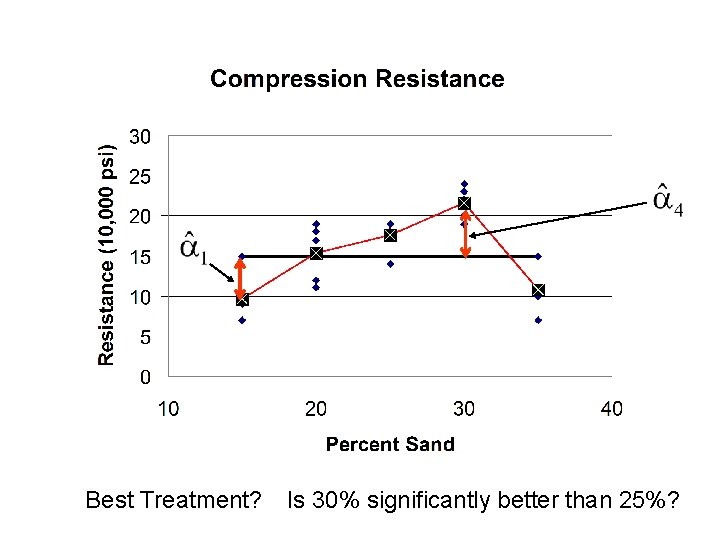
Best Treatment? Is 30% significantly better than 25%?

Estimation

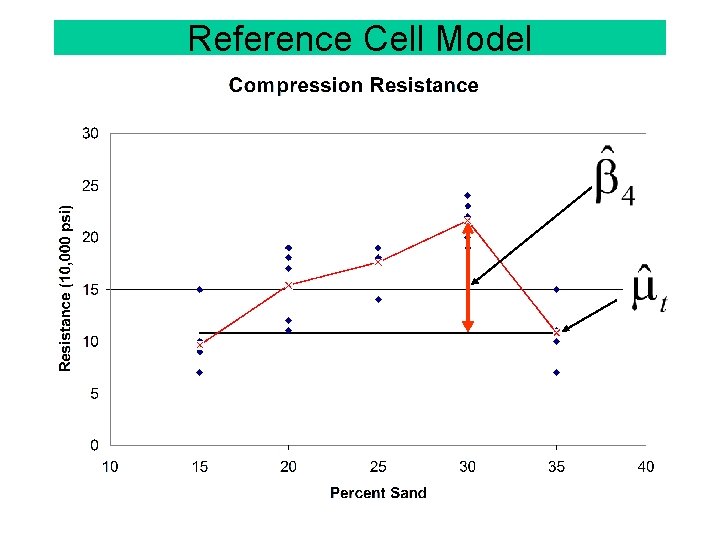
Reference Group/Cell Model: random error ~ N(0, s 2) reference group effect due to population i mean Mean for the last group (i=t) is t. Mean for the first group (i=1) is t + b 1 Thus, b 1 is the difference between the mean of the reference group (cell) and the target group mean. Any group can be the reference group. This is the model SASâ uses. All bi = 0 implies all groups have the same mean.

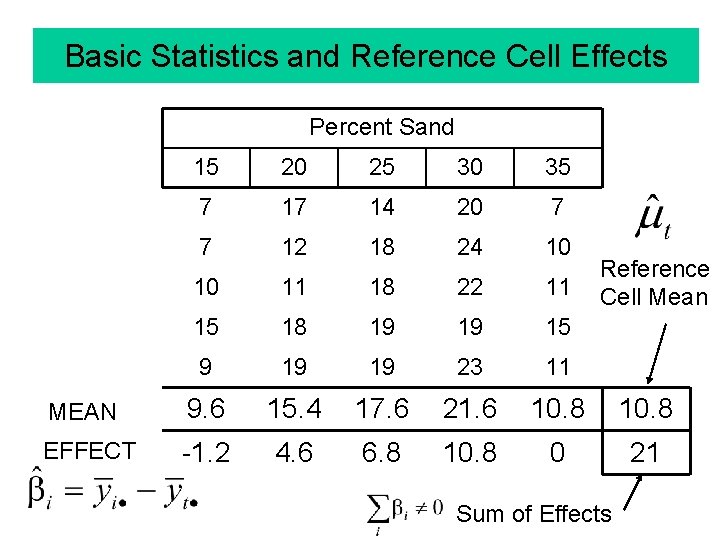
Basic Statistics and Reference Cell Effects Percent Sand 15 20 25 30 35 7 17 14 20 7 7 12 18 24 10 10 11 18 22 11 15 18 19 19 15 9 19 19 23 11 MEAN 9. 6 15. 4 17. 6 21. 6 10. 8 EFFECT -1. 2 4. 6 6. 8 10. 8 0 21 Reference Cell Mean Sum of Effects

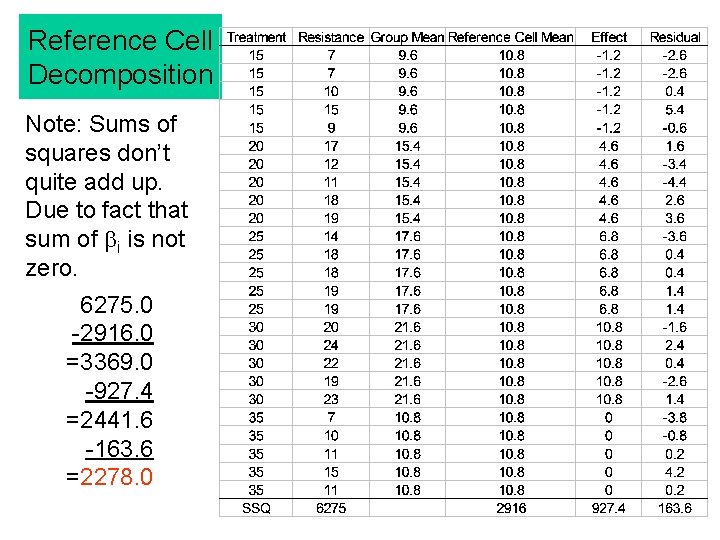
Reference Cell Decomposition Note: Sums of squares don’t quite add up. Due to fact that sum of bi is not zero. 6275. 0 -2916. 0 =3369. 0 -927. 4 =2441. 6 -163. 6 =2278. 0

Decomposing Sums of Squares 6275 = 2916. 0 + 927. 4 + 163. 4 + 2278

Reference Cell Model

SAS Program options ls=78 ps=49 nodate; data stress; input sand resistance @@; datalines; 15 7 15 10 15 15 15 9 20 17 20 12 20 11 20 18 20 19 25 14 25 18 25 19 30 20 30 24 30 22 30 19 30 23 35 7 35 10 35 11 35 15 35 11 ; proc glm data=stress; class sand; model resistance = sand / solution; title 2 'Compression resistance in concrete beams as'; title 2 ' a function of percent sand in the mix'; run;

SAS Output(1) Compression resistance in concrete beams as a function of percent sand in the mix The GLM Procedure Dependent Variable: resistance Sum of Source DF Squares Mean Square F Value Pr > F Model 4 486. 4000000 121. 6000000 14. 87 <. 0001 Error 20 163. 6000000 8. 1800000 Corrected Total 24 650. 0000000 R-Square Coeff Var Root MSE resistance Mean 0. 748308 19. 06713 2. 860070 15. 00000

SAS Output(2) Source sand DF Type I SS Mean Square F Value Pr > F 4 486. 4000000 121. 6000000 14. 87 <. 0001 DF Type III SS Mean Square F Value Pr > F 4 486. 4000000 121. 6000000 14. 87 <. 0001 Standard Parameter Estimate Error t Value Pr > |t| Intercept 10. 80000000 B 1. 27906216 8. 44 <. 0001 sand 15 -1. 20000000 B 1. 80886705 -0. 66 0. 5146 sand 20 4. 60000000 B 1. 80886705 2. 54 0. 0194 sand 25 6. 80000000 B 1. 80886705 3. 76 0. 0012 sand 30 10. 80000000 B 1. 80886705 5. 97 <. 0001 sand 35 0. 0000 B . . . NOTE: The X'X matrix has been found to be singular, and a generalized inverse was used to solve the normal equations. Terms whose estimates are followed by the letter 'B' are not uniquely estimable.

Minitab One-way ANOVA: Resist versus Sand Analysis of Variance for Resist Source DF SS MS F P Sand 4 486. 40 121. 60 14. 87 0. 000 Error 20 163. 60 8. 18 Total 24 650. 00 Individual 95% CIs For Mean Based on Pooled St. Dev Level N Mean St. Dev 15 5 9. 600 3. 286 20 5 15. 400 3. 647 25 5 17. 600 2. 074 30 5 21. 600 2. 074 35 5 10. 800 2. 864 -------+---------+----(----*-----) (-----*----) -------+---------+----- Pooled St. Dev = 2. 860 10. 0 15. 0 20. 0

Minitab Stat ANOVA One-Way Multiple comparisons (later)

Minitab Dot Plot

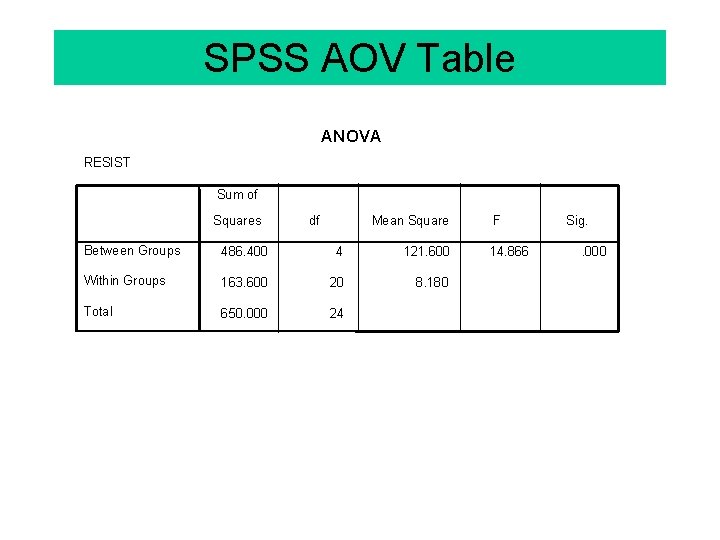
SPSS AOV Table ANOVA RESIST Sum of Squares df Mean Square Between Groups 486. 400 4 121. 600 Within Groups 163. 600 20 8. 180 Total 650. 000 24 F 14. 866 Sig. . 000

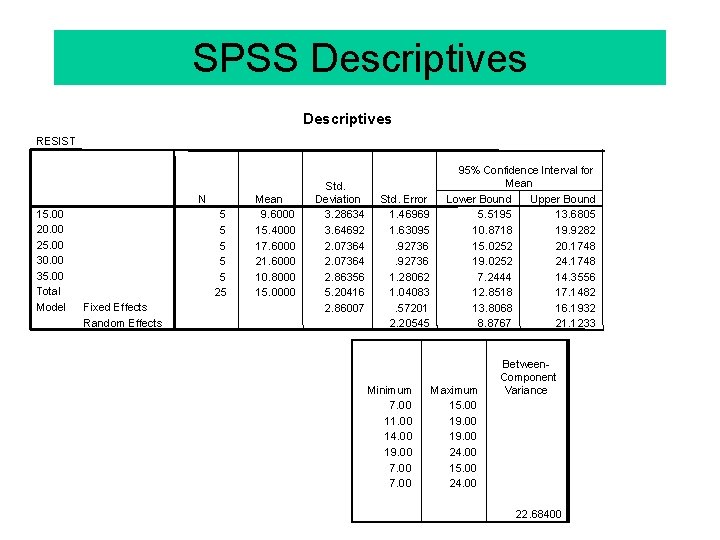
SPSS Descriptives RESIST N 15. 00 20. 00 25. 00 30. 00 35. 00 Total Model 5 5 5 25 Fixed Effects Random Effects Mean 9. 6000 15. 4000 17. 6000 21. 6000 10. 8000 15. 0000 Std. Deviation 3. 28634 3. 64692 2. 07364 2. 86356 5. 20416 2. 86007 Std. Error 1. 46969 1. 63095. 92736 1. 28062 1. 04083. 57201 2. 20545 Minimum 7. 00 11. 00 14. 00 19. 00 7. 00 95% Confidence Interval for Mean Lower Bound Upper Bound 5. 5195 13. 6805 10. 8718 19. 9282 15. 0252 20. 1748 19. 0252 24. 1748 7. 2444 14. 3556 12. 8518 17. 1482 13. 8068 16. 1932 8. 8767 21. 1233 Maximum 15. 00 19. 00 24. 00 15. 00 24. 00 Between. Component Variance 22. 68400

CRD Analysis in R > resist <- c(7, 7, 10, 15, 9, 17, 12, 11, 18, 19, 14, …, 19, 23, 7, 10, 11, 15, 11) > sand <- factor(rep(seq(15, 35, 5), rep(5, 5))) > myfit <- aov(resist~sand) > summary(myfit) Df Sum Sq Mean Sq F value sand 4 486. 40 121. 60 14. 866 Residuals 20 163. 60 8. 18 --Signif. codes: 0 `***' 0. 001 `**' 0. 01 `*' 0. 05 `. ' 0. 1 ` ' 1 > coef(myfit) (Intercept) sand 20 9. 6 5. 8 sand 25 8. 0 sand 30 12. 0 Pr(>F) 8. 655 e-06 *** sand 35 1. 2 R functions aov() & lm() by default reference first cell mean!

Fixed Effects Normally, the “effect” of a particular treatment is assumed to be a constant value (ai) added to the response of all units in the group receiving the treatment. If the treatments are well defined, easily replicable and are expected to produce the same effect on average in each replicate, we have a fixed set of treatments and the AOV model is said to describe a fixed effects model. Examples: • A scientist develops 3 new fungicides. Her interest is in these fungicides only. • The impact of 4 specific soil types on plant growth are of interest. • Three particular milling machines are being compared. • Four particular lakes are of interest in their weed biomass densities. • Three tests for assessing developmental learning are being compared.

Random Effects If the treatments cannot be assumed to be from a prespecified or known set of treatments, they are assumed to be a random sample from some larger population of potential treatments. In this case, the AOV model is called a random effects model and the ai are called random effects. Examples: • A scientist is interested in how fungicides work. Ten (10) fungicides are selected (at random) to represent the population of all fungicides in the research (plots as replicates). • Four soil sub groups are selected for examining plant growth (pots as replicates). • Three milling machines selected at random from the production line are compared (runs as replicates). • 16 lakes selected at random are measured for their weed biomass densities (water samples as replicates). • A standard test for development is given to 20 middle school classes selected at random from the over 200 available among all middle schools in the county (student as replicate). In each case, we assume the values for the effects would change if our sample had changed. Inference is directed not to answering “which treatment is different from which other treatment? ” but to the issue of “is the variability among treatments significantly greater than the residual variability? ”.

Closing Comments on CRD Even though we have introduced several variations on the same basic model for defining “effects”, the final F-test for the hypothesis of overall equal group means is the same one developed as part of the analysis of variance. It turns out that there may be computational advantages to using the one formulation of the model over another, but this has absolutely no effect on the hypothesis test. We will see this in the next Section. For simple one-factor designs, whether the treatment effect is considered random or fixed, the F-test is the same, the interpretation is different.