Randomized Algorithms Deterministic Vs Randomized Algorithms Deterministic Algorithms

Randomized Algorithms

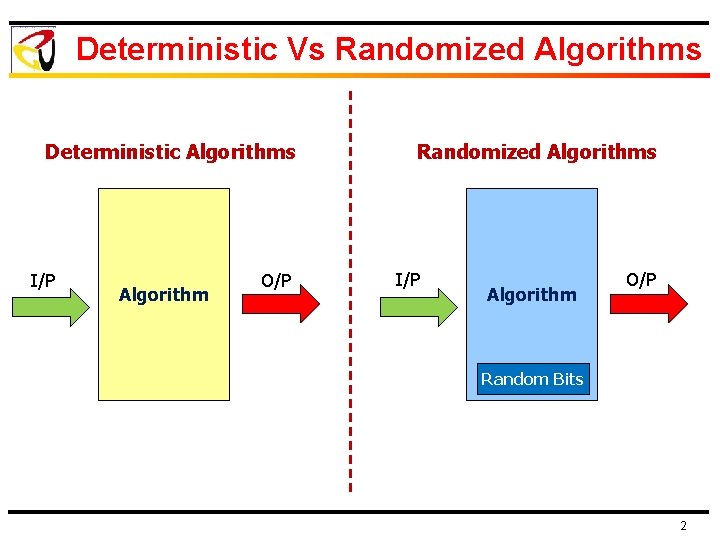
Deterministic Vs Randomized Algorithms Deterministic Algorithms I/P Algorithm O/P Randomized Algorithms I/P Algorithm O/P Random Bits 2

What are Randomized Algorithms? Ø Algorithms whose behavior depends on: Ø Input(s) Ø A sequence of random bits (these random bits lead to: random steps, choices, decisions, …, etc. during the running of the algorithm) Ø Can be faster and simpler than a deterministic algorithm Ø Two types: Ø Las Vegas Ø Mont Carlo 3

Las Vegas or Mont Carlo Las Vegas Mont Carlo Ø Always returns Correct answer Ø Always runs Fast Ø Running time Fast with a High Probability Ø Returns Correct answer with a High Probability 4

Example 1 Ø Input: array of n chars, half ‘a’s, half ‘b’s Ø Problem: Find location of any ‘a’ Ø Deterministic Approach: Ø Search One by One worst case: O(n/2) Ø Randomized Approach: Ø Ø Check entries at random until ‘a’ is found Probability of finding ‘a’ right away = 0. 5 Probability of missing ‘a’ k times in a row = 0. 5 k Which type of algorithm is it? 5

Example 2: Microchip Test Ø We want to know if the manufacturer tested a batch of chips Ø For an untested batch, P(bad) = 0. 1 Ø Deterministic Algorithm: test them all O(n) Ø Randomized Algorithm: test chips at random 6

Example 2: Microchip Test Ø Question to ask: “Has this batch NOT been tested? ” Ø TRUE – if random algorithm finds a bad chip Ø UNKNOWN – if algorithm finds a good chip Ø After k chips, algorithm concludes FALSE, therefore the batch is GOOD. Ø Probability a good chip came from untested batch = 0. 9 Ø Probability “good” batch is actually bad = 0. 9 k 7

Example 2: Microchip Test Ø 0. 9 k = probability a bad batch is being tested and we keep finding the good chips, k times in a row Ø For k = 66, chances of a bad batch slipping through is less than 1 in a 1000 => small Ø Running time = O(k), independent of n, determined by k set by programmer => fast Ø Monte Carlo: running time fast, correctness probability high 8

Example 3: Min-Cut Ø Input: A connected, undirected graph G = (V, E) Ø Output: A min-cut, i. e. smallest set of edges to remove that splits graph into two Ø Possible approaches: Ø Try them all – exponential since there are 2|E| subsets of edges Ø Modified max-flow algorithm for all s-t pairs – O(|V|3) x O(|V|2) pairs of vertices = O(|V|5)

Example 3: Min-Cut Ø Randomized approach: O((nlogn)2) Ø Same idea as chip test: Ø one time through the algorithm yields a relatively low probability of success Ø repeat algorithm to reduce probability of repeated failure until satisfied with probability of success Ø Will only show algorithm and that it works with a certain probability of success

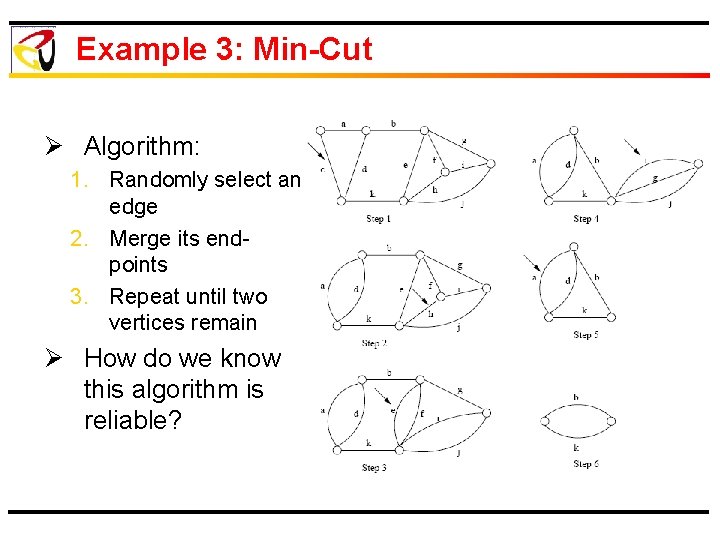
Example 3: Min-Cut Ø Algorithm: 1. Randomly select an edge 2. Merge its endpoints 3. Repeat until two vertices remain Ø How do we know this algorithm is reliable?

Analysis I Ø Min-cut is small---few edges Ø Ø Ø Suppose graph has min-cut c Then minimum degree at least c Thus at least nc/2 edges Ø Random edge is probably safe Ø Pr[min-cut edge] £ c/(nc/2) Ø = 2/n

Analysis II Ø Algorithm succeeds if never accidentally contracts min-cut edge Ø Contracts #vertices from n down to 2 Ø When k vertices, chance of error is 2/k Ø thus, chance of being right is 1 -2/k Ø Pr[always right] is product of probabilities of being right each time

Analysis III …not too good!

Repetition amplifies success probability Ø Ø basic failure probability 1 - 2/n 2 so repeat 7 n 2 times