Outline Full space half space and quarter space









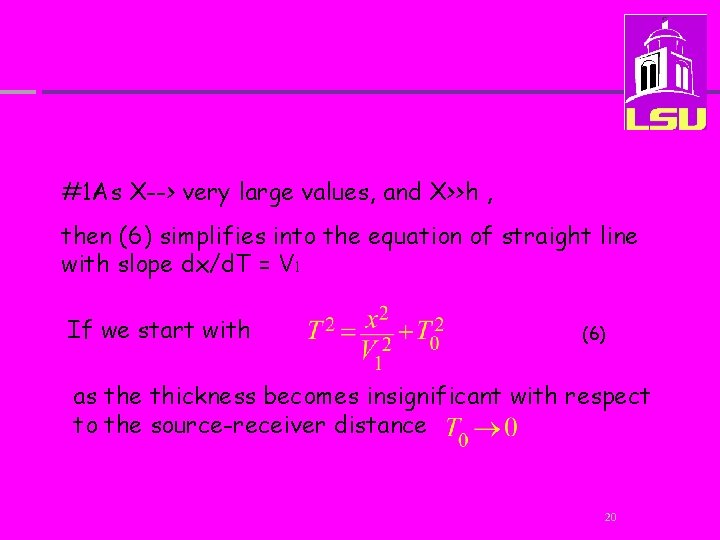










































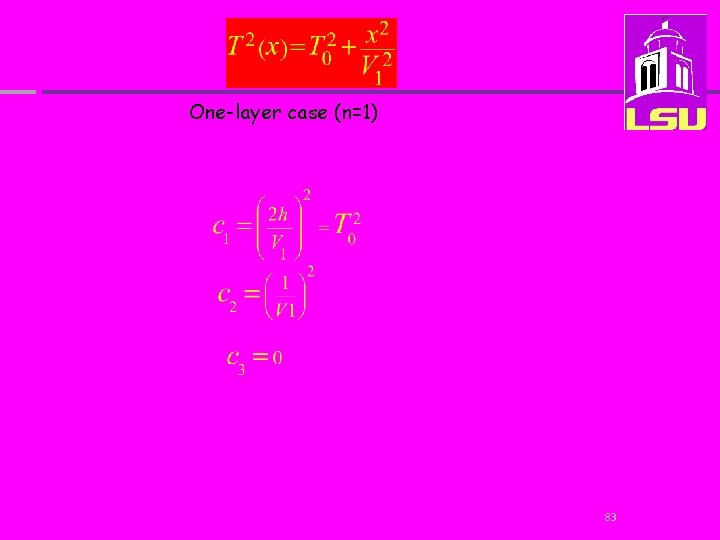




- Slides: 91

Outline • Full space, half space and quarter space • Traveltime curves of direct ground- and air- waves and rays • Error analysis of direct waves and rays • Constant-velocity-layered half-space • Constant-velocity versus Gradient layers • Reflections • Scattering Coefficients 1

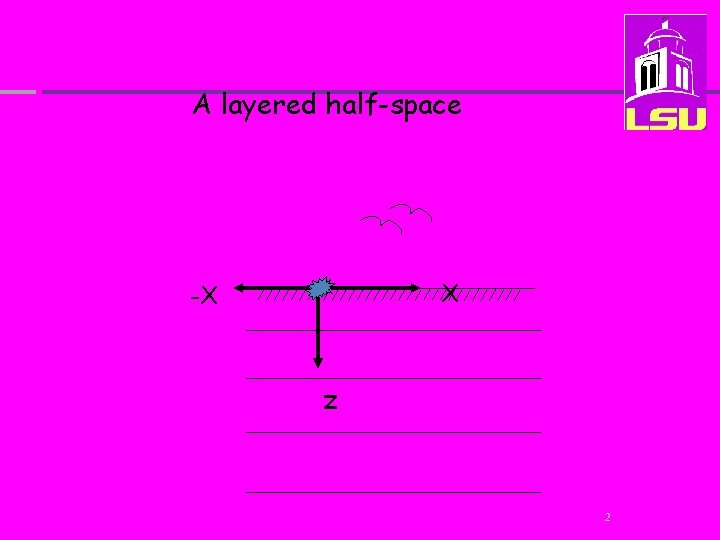
A layered half-space X -X z 2

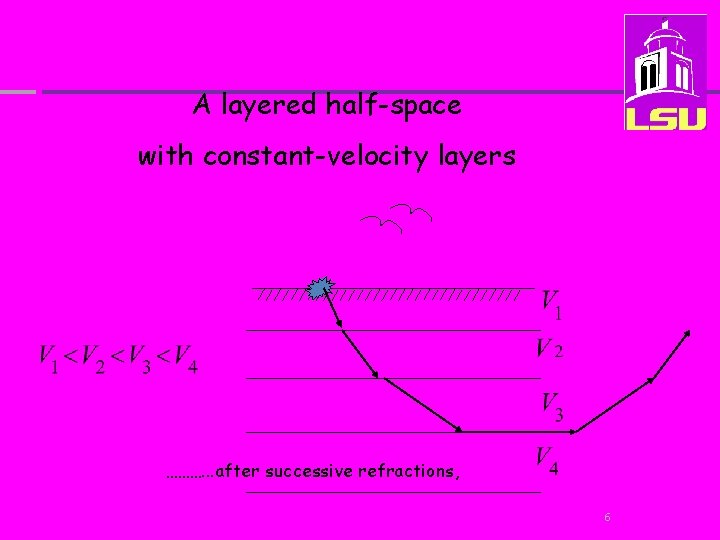
A layered half-space with constant-velocity layers Eventually, …. . 3

A layered half-space with constant-velocity layers Eventually, …. . 4

A layered half-space with constant-velocity layers Eventually, …. . 5

A layered half-space with constant-velocity layers ………. . . after successive refractions, 6

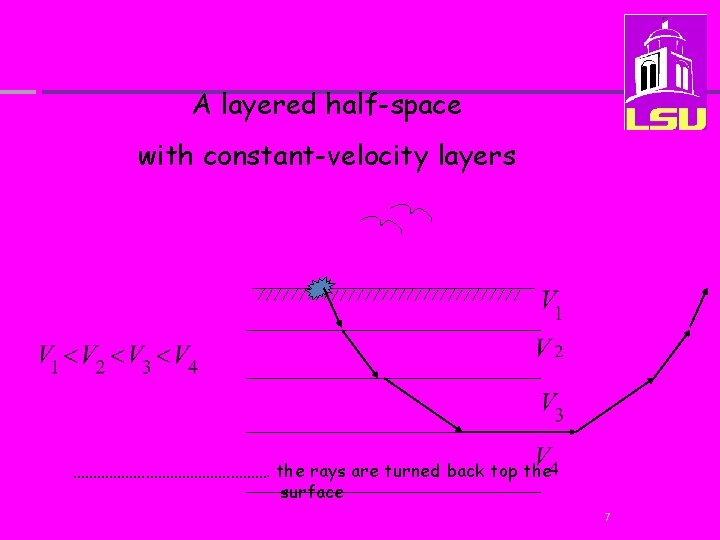
A layered half-space with constant-velocity layers ……………………. the rays are turned back top the surface 7

Outline • Full space, half space and quarter space • Traveltime curves of direct ground- and air- waves and rays • Error analysis of direct waves and rays • Constant-velocity-layered half-space • Constant-velocity versus gradient layers • Reflections • Scattering Coefficients 8

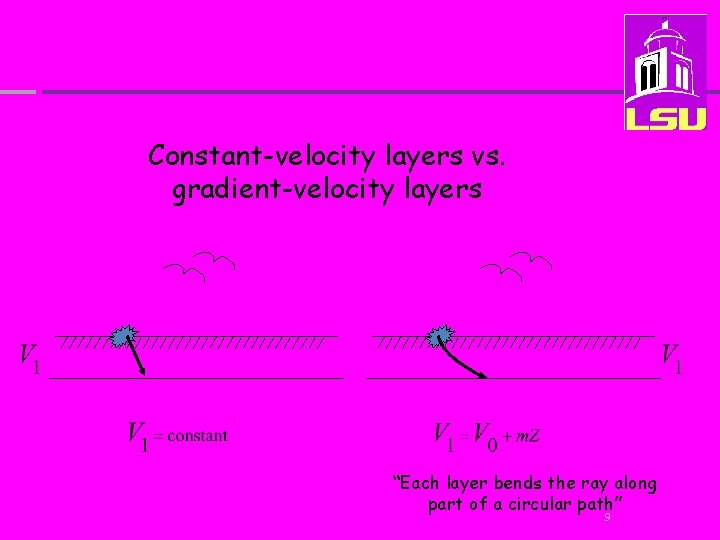
Constant-velocity layers vs. gradient-velocity layers “Each layer bends the ray along part of a circular path” 9

Outline • Full space, half space and quarter space • Traveltime curves of direct ground- and air- waves and rays • Error analysis of direct waves and rays • Constant-velocity-layered half-space • Constant-velocity versus gradient layers • Reflections • Scattering Coefficients 10

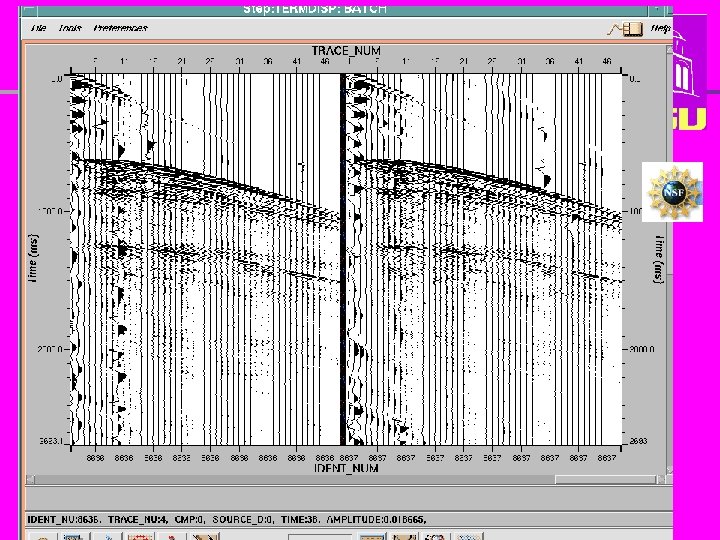
11

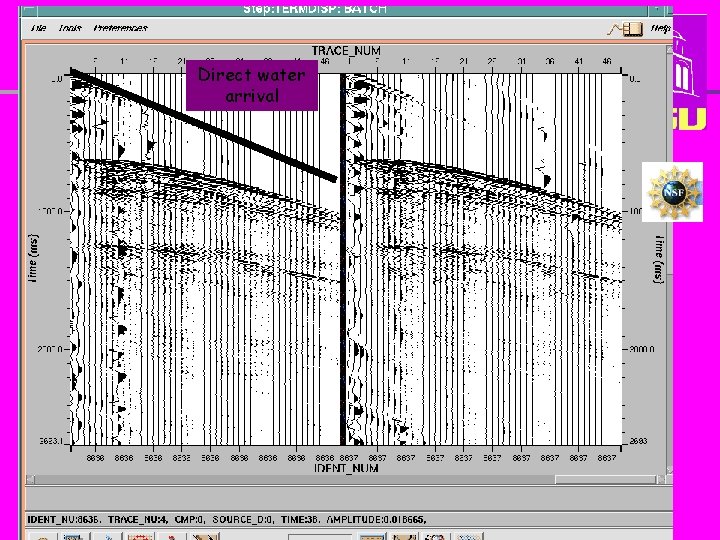
Direct water arrival 12

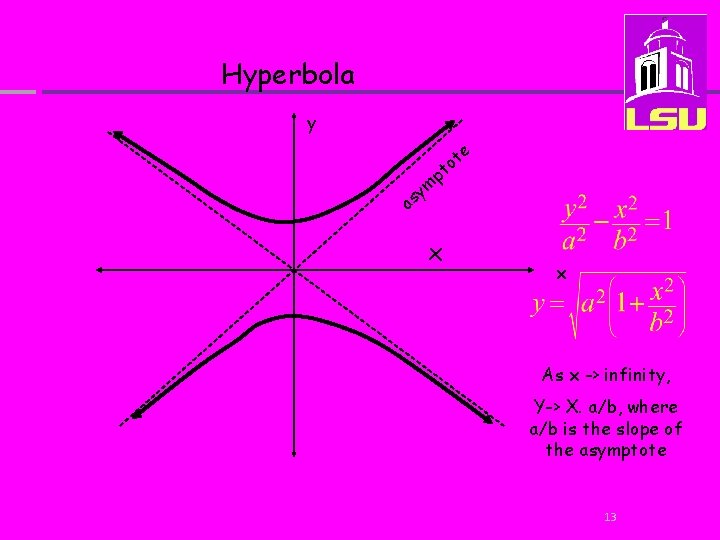
Hyperbola y p ym s a x e t o t x As x -> infinity, Y-> X. a/b, where a/b is the slope of the asymptote 13

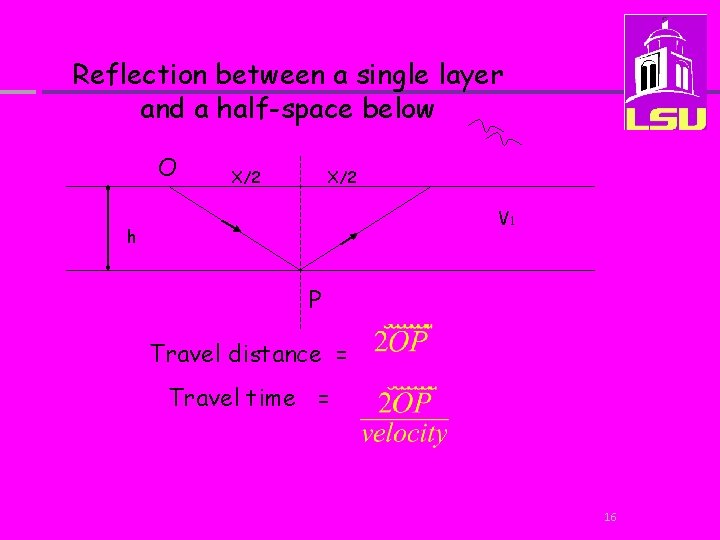
Reflection between a single layer and a half-space below O X/2 V 1 h P Travel distance = ? Travel time = ? 14

Reflection between a single layer and a half-space below O X/2 V 1 h P Travel distance = ? Travel time = ? Consider the reflecting ray……. as follows …. 15

Reflection between a single layer and a half-space below O X/2 V 1 h P Travel distance = Travel time = 16

Reflection between a single layer and a half-space below Traveltime = (6) 17

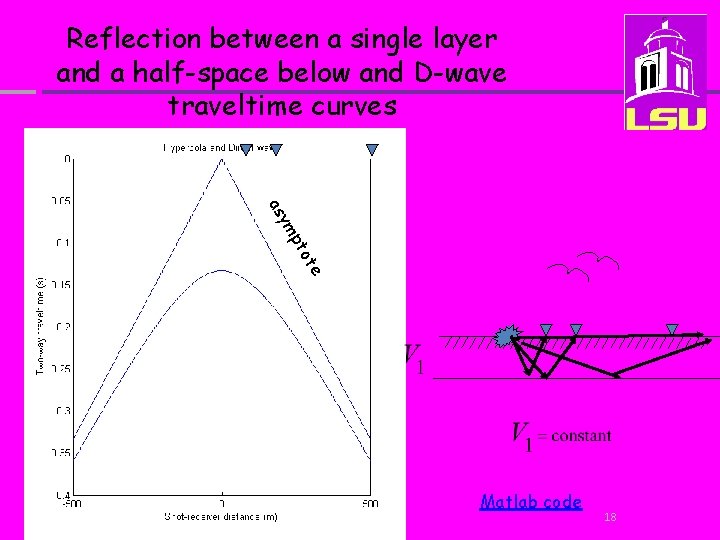
Reflection between a single layer and a half-space below and D-wave traveltime curves te to mp y as Matlab code 18

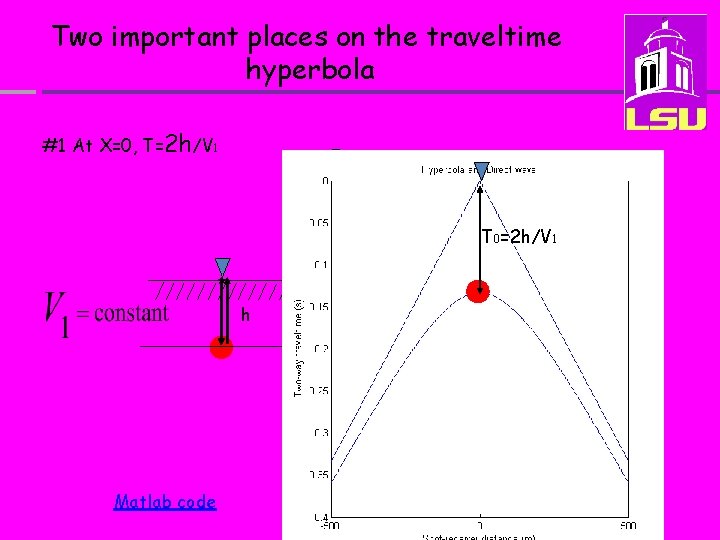
Two important places on the traveltime hyperbola #1 At X=0, T=2 h/V 1 T 0=2 h/V 1 * h Matlab code 19
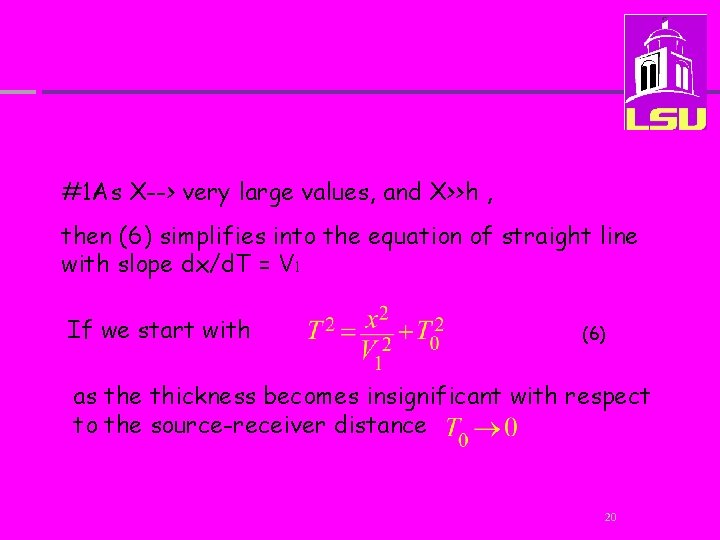
#1 As X--> very large values, and X>>h , then (6) simplifies into the equation of straight line with slope dx/d. T = V 1 If we start with (6) as the thickness becomes insignificant with respect to the source-receiver distance 20

By analogy with the parametric equation for a hyperbola, the slope of this line is 1/V 1 i. e. a/b = 1/V 1 21

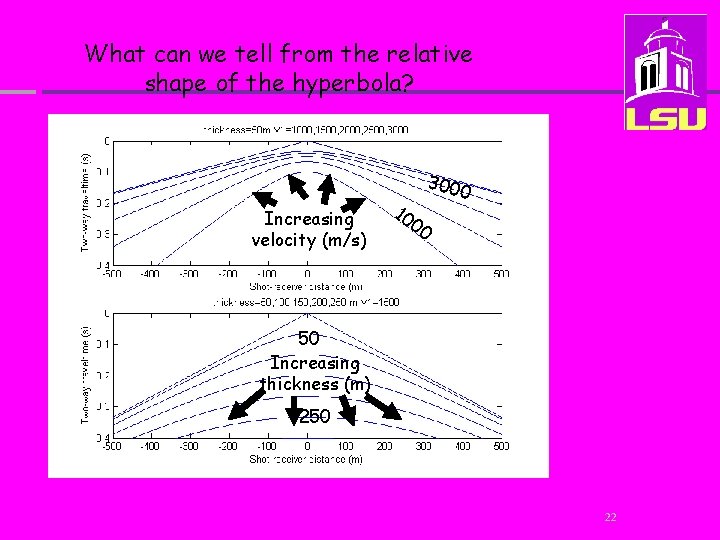
What can we tell from the relative shape of the hyperbola? Increasing velocity (m/s) 10 00 300 0 50 Increasing thickness (m) 250 22

“Greater velocities, and greater thicknesses flatten the shape of the hyperbola, all else remaining constant” 23

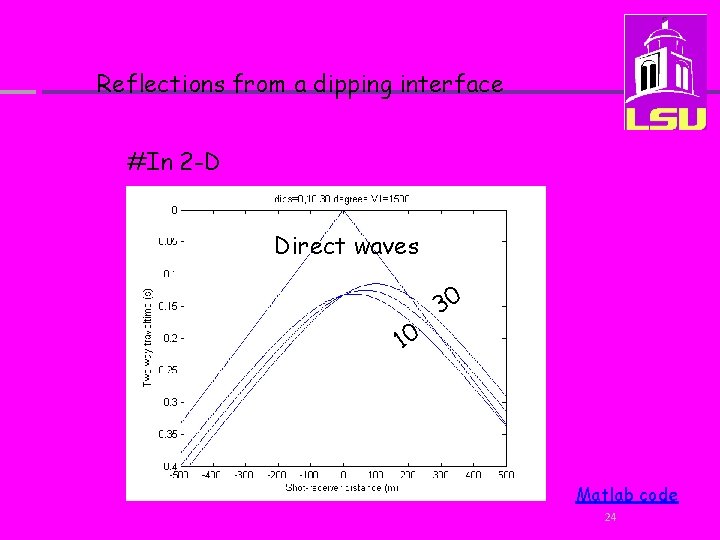
Reflections from a dipping interface #In 2 -D Direct waves 10 30 Matlab code 24

Reflections from a 2 D dipping interface #In 2 -D: “The apex of the hyperbola moves in the geological, updip direction to lesser times as the dip increases” 25

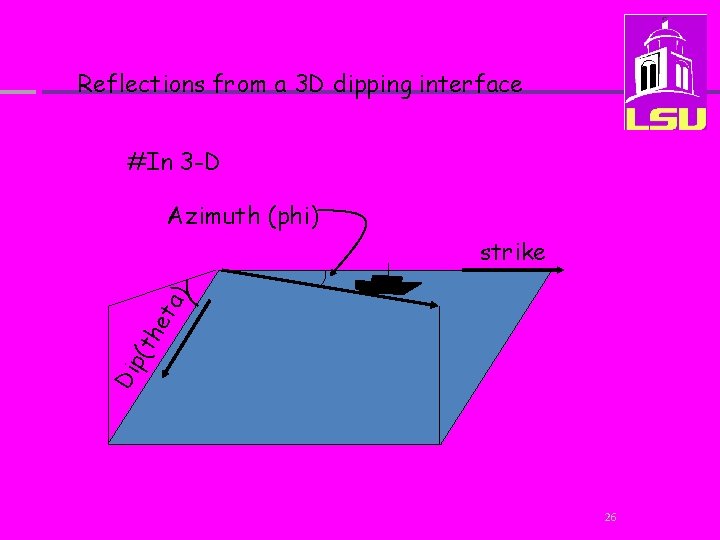
Reflections from a 3 D dipping interface #In 3 -D Azimuth (phi) Di p(t he t a) strike 26

Reflections from a 3 D dipping interface #In 3 -D Direct waves 0 90 Matlab code 27

Reflections from a 2 D dipping interface #In 3 -D: “The apparent dip of a dipping interface grows from 0 toward the maximum dip as we increase the azimuth with respect to the strike of the dipping interface” 28

Outline • Full space, half space and quarter space • Traveltime curves of direct ground- and air- waves and rays • Error analysis of direct waves and rays • Constant-velocity-layered half-space • Constant-velocity versus Gradient layers • Reflections • Scattering Coefficients 29

Amplitude of a traveling wave is affected by…. • Scattering Coefficient Amp = Amp(change in Acoustic Impedance (I)) • Geometric spreading Amp = Amp(r) • Attenuation (inelastic, frictional loss of energy) Amp = Amp(r, f) 30

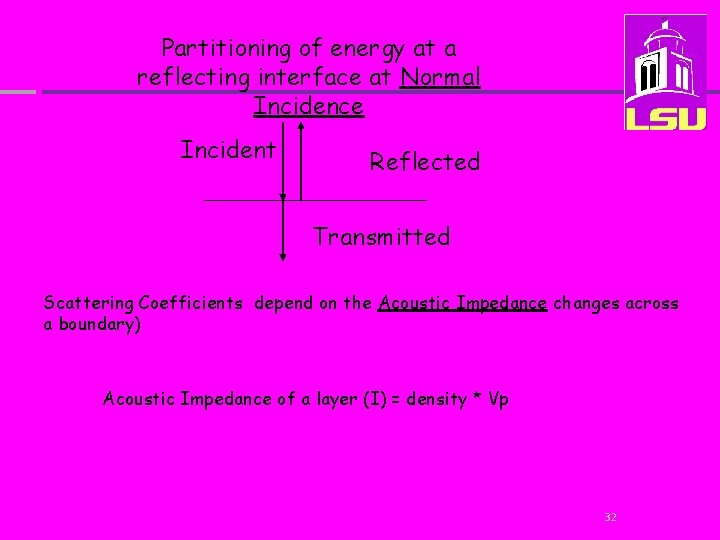
Partitioning of energy at a reflecting interface at Normal Incidence Incident Reflected Transmitted Incident Amplitude = Reflected Amplitude + Transmitted Amplitude Reflected Amplitude = Incident Amplitude Transmitted. Amplitude = Incident Amplitude x Reflection Coefficient x Transmission Coefficient 31

Partitioning of energy at a reflecting interface at Normal Incidence Incident Reflected Transmitted Scattering Coefficients depend on the Acoustic Impedance changes across a boundary) Acoustic Impedance of a layer (I) = density * Vp 32

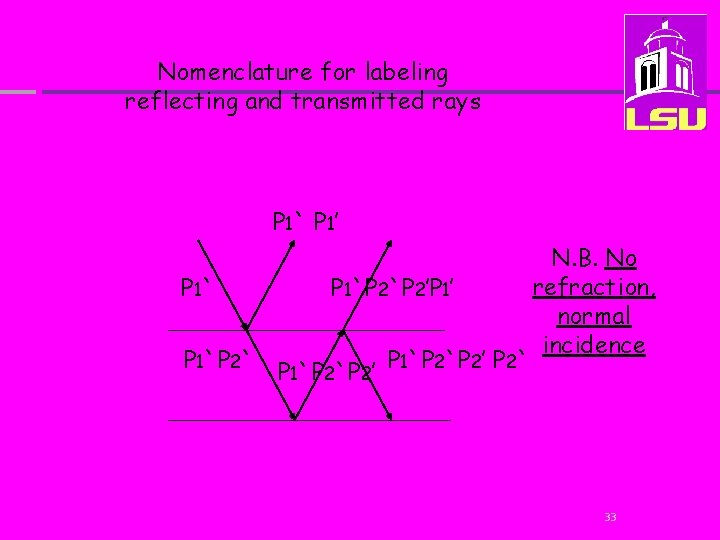
Nomenclature for labeling reflecting and transmitted rays P 1` P 1’ P 1`P 2`P 2’P 1’ P 1`P 2`P 2’ P 1`P 2’ P 2` N. B. No refraction, normal incidence 33

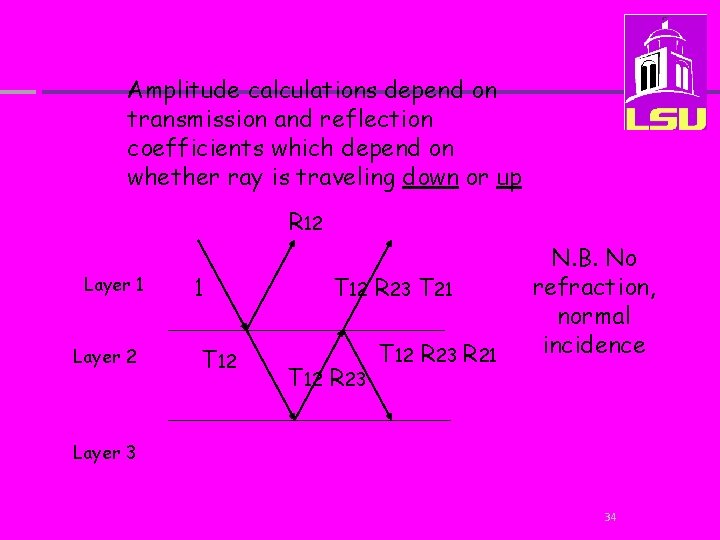
Amplitude calculations depend on transmission and reflection coefficients which depend on whether ray is traveling down or up R 12 Layer 1 Layer 2 1 T 12 R 23 T 21 T 12 R 23 R 21 N. B. No refraction, normal incidence Layer 3 34

Reflection Coefficients R 12 = (I 2 -I 1) / (I 1+I 2) R 21 = (I 1 -I 2) / (I 2+I 1) Transmission Coefficients T 12 = 2 I 1 / (I 1+I 2) T 21 = 2 I 2 / (I 2+I 1) 35

Example of Air-water reflection Air: density =0; Vp=330 m/s water: density =1; Vp=1500 m/s Layer 1 Layer 2 Air Water 36

Example of Air-water reflection Air: density =0; Vp=330 m/s water: density =1; Vp=1500 m/s R 12 = (I 2 -I 1) / (I 1+I 2) 37

Example of Air-water reflection Air: density =0; Vp=330 m/s water: density =1; Vp=1500 m/s R 12 = (I 2 -I 1) / (I 1+I 2) RAir. Water = (IWater-IAir) / (IAir+IWater) 38

Example of Air-water reflection Air: density =0; Vp=330 m/s water: density =1; Vp=1500 m/s R 12 = (I 2 -I 1) / (I 2+I 1) RAir. Water = (IWater-IAir) / (IAir+IWater) RAir. Water = (IWater-0) / (0+IWater) RAir. Water = 1 39

Example of Water-air reflection Air: density =0; Vp=330 m/s water: density =1; Vp=1500 m/s Layer 1 Layer 2 Air Water 40

Example of Water-air reflection Air: density =0; Vp=330 m/s water: density =1; Vp=1500 m/s R 21 = (I 1 -I 2) / (I 1+I 2) 41

Example of Water-air reflection Air: density =0; Vp=330 m/s water: density =1; Vp=1500 m/s R 22 = (I 1 -I 2) / (I 1+I 2) RWater. Air = (IAir-IWater) / (IAir+IWater) 42

Example of Water-air reflection Air: density =0; Vp=330 m/s water: density =1; Vp=1500 m/s R 21 = (I 1 -I 2) / (I 1+I 2) RWater. Air = (IAir-IWater) / (IAir+IWater) RWater. Air = (0 -IWater) / (0+IWater) RWater. Air = -1 ( A negative reflection coefficient) 43

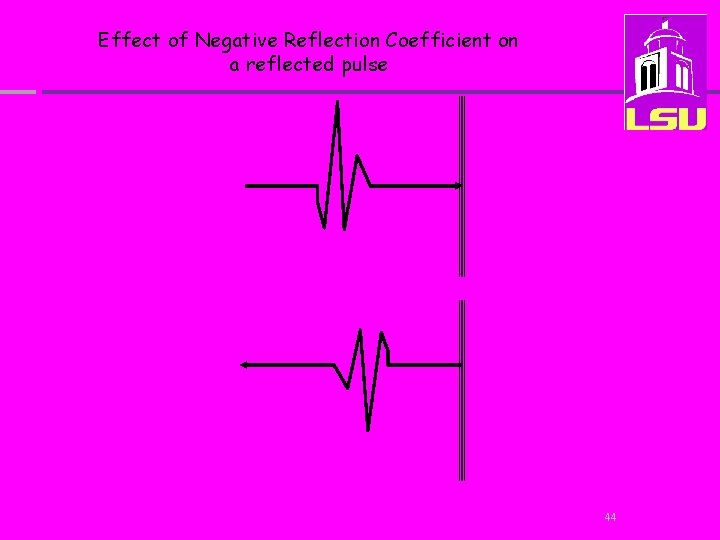
Effect of Negative Reflection Coefficient on a reflected pulse 44

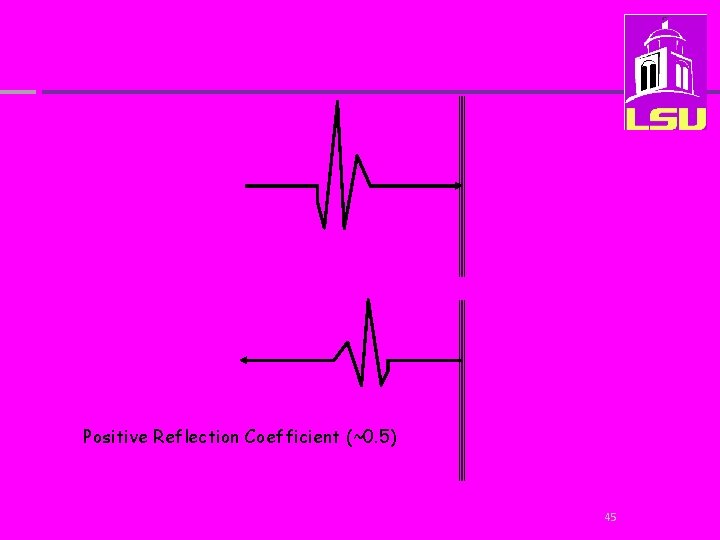
Positive Reflection Coefficient (~0. 5) 45

“Water-air interface is a near-perfect reflector” 46

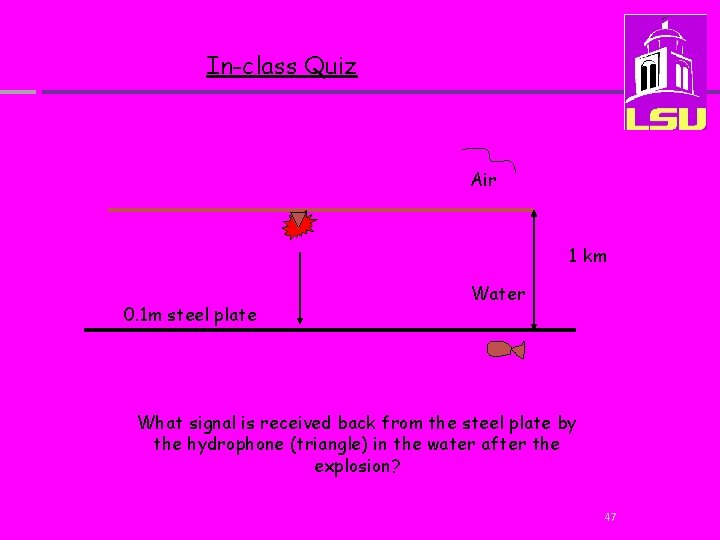
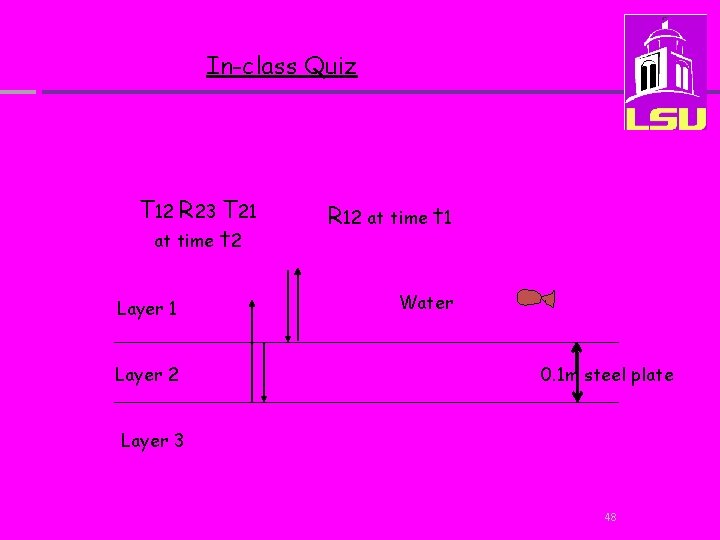
In-class Quiz Air 1 km 0. 1 m steel plate Water What signal is received back from the steel plate by the hydrophone (triangle) in the water after the explosion? 47

In-class Quiz T 12 R 23 T 21 at time t 2 Layer 1 Layer 2 R 12 at time t 1 Water 0. 1 m steel plate Layer 3 48

Steel: density = 8; Vp=6000 m/s water: density =1; Vp=1500 m/s R 12 = (I 2 -I 1) / (I 1+I 2) RWater. Steel = (Isteel-Iwater) / (Isteel+Iwater) 49

Steel: density = 8; Vp=6000 m/s; I=48, 000 water: density =1; Vp=1500 m/s; 1500 R 12 = (I 2 -I 1) / (I 1+I 2) RWater. Steel = (Isteel-Iwater) / (Isteel+Iwater) RWater. Steel = (46, 500) / (49, 500) RWater. Steel = 0. 94 50

Steel: density = 8; Vp=6000 m/s; I=48, 000 water: density =1; Vp=1500 m/s; 1500 R 21 = (I 1 -I 2) / (I 1+I 2) RSteel water= (Iwater-Isteel) / (Iwater+Isteel) RSteel water= (-46, 500) / (49, 500) Rsteel water = -0. 94 51

Steel: density = 8; Vp=6000 m/s ; I=48, 000 water: density =1; Vp=1500 m/s; I=1500 T 12 = 2 I 1/ (I 1+I 2) T Water. Steel= 2 IWater/ (Iwater+Isteel) T Water. Steel= 3000/ (49, 500) T Water. Steel= 0. 06 52

Steel: density = 8; Vp=6000 m/s ; I=48, 000 water: density =1; Vp=1500 m/s; I=1500 T 21 = 2 I 2/ (I 1+I 2) T Steel. Water= 2 ISteel/ (Iwater+Isteel) T Steel. Water= 96, 000/ (49, 500) T Steel. Water= 1. 94 53

For a reference incident amplitude of 1 At t 1: Amplitude = R 12 = 0. 94 At t 2: Amplitude = T 12 R 23 T 21 = 0. 06 x -0. 94 x 1. 94 = -0. 11 at t 2 -t 1 = 2*0. 1 m/6000 m/s in steel =0. 00005 s =5/100 ms 54

Summation of two “realistic” wavelets 55

Either way, the answer is yes!!! 56

Outline-2 • AVA-- Angular reflection coefficients • Vertical Resolution • Fresnel- horizontal resolution • Headwaves • Diffraction • Ghosts • Land • Marine • Velocity layering • “approximately hyperbolic equations” • multiples 57

Variation of Amplitude with angle (“AVA”) for the fluid-over-fluid case (NO SHEAR WAVES) “As the angle of incidence is increased the amplitude of the reflecting wave changes” (7) (Liner, 2004; Eq. 3. 29, p. 68) 58

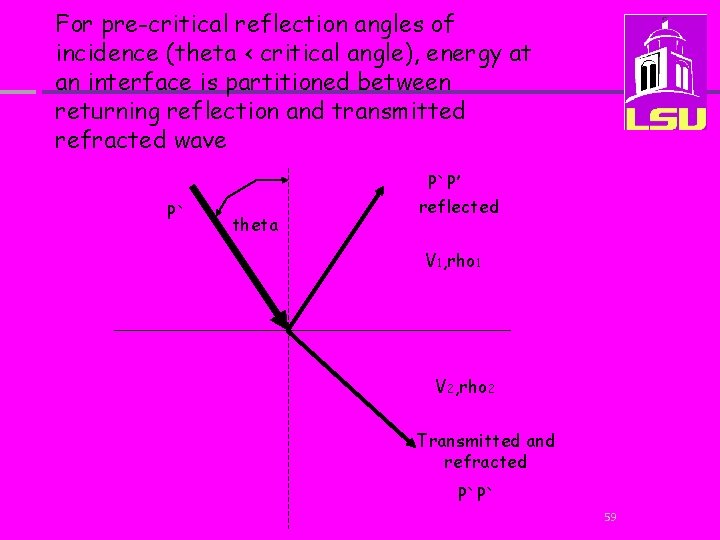
For pre-critical reflection angles of incidence (theta < critical angle), energy at an interface is partitioned between returning reflection and transmitted refracted wave P` theta P`P’ reflected V 1, rho 1 V 2, rho 2 Transmitted and refracted P`P` 59

Matlab Code 60

What happens to the equation 7 as we reach the critical angle? 61

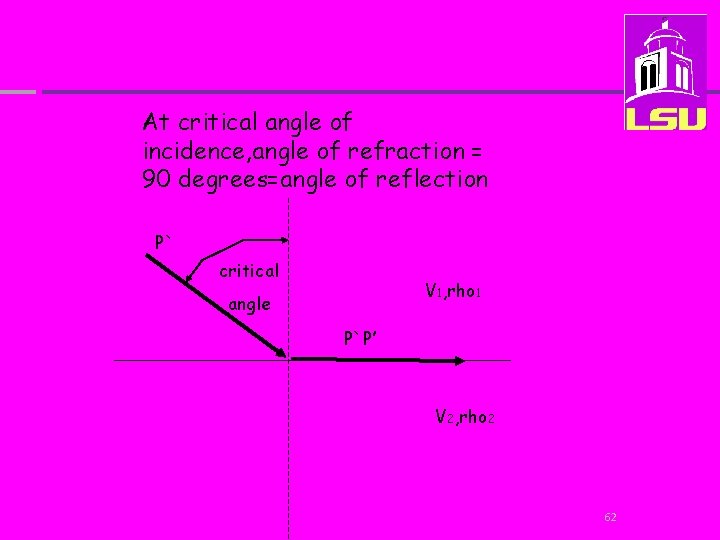
At critical angle of incidence, angle of refraction = 90 degrees=angle of reflection P` critical V 1, rho 1 angle P`P’ V 2, rho 2 62

At criticality, The above equation becomes: 63

For angle of incidence > critical angle; angle of reflection = angle of incidence and there are no refracted waves i. e. TOTAL INTERNAL REFLECTION P` critical V 1, rho 1 angle P`P’ V 2, rho 2 64

The values inside the square root signs can be negative, so that the numerator, denominator and reflection coefficient become complex numbers 65

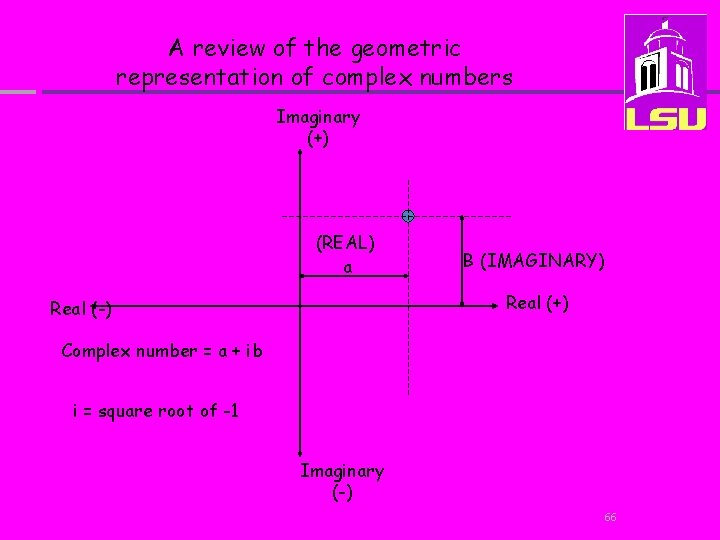
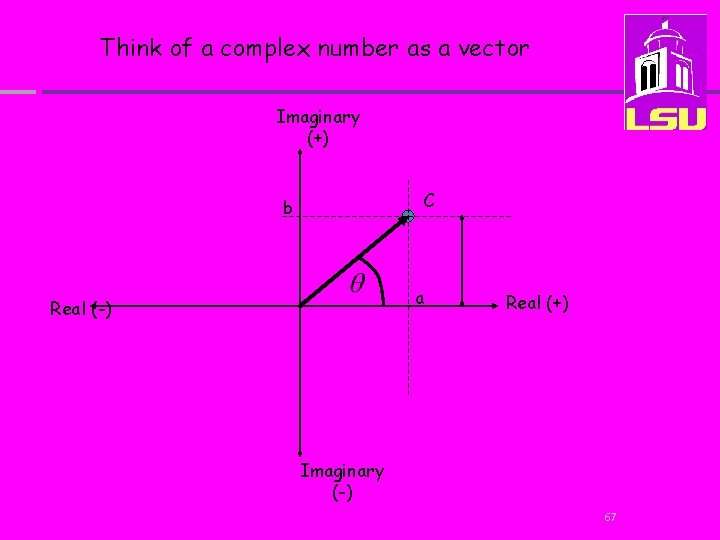
A review of the geometric representation of complex numbers Imaginary (+) (REAL) a B (IMAGINARY) Real (+) Real (-) Complex number = a + ib i = square root of -1 Imaginary (-) 66

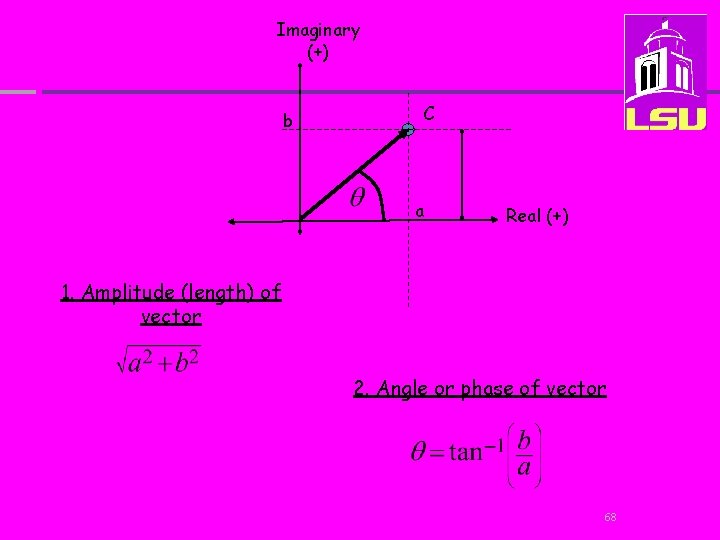
Think of a complex number as a vector Imaginary (+) C b a Real (-) Real (+) Imaginary (-) 67

Imaginary (+) b C a Real (+) 1. Amplitude (length) of vector 2. Angle or phase of vector 68

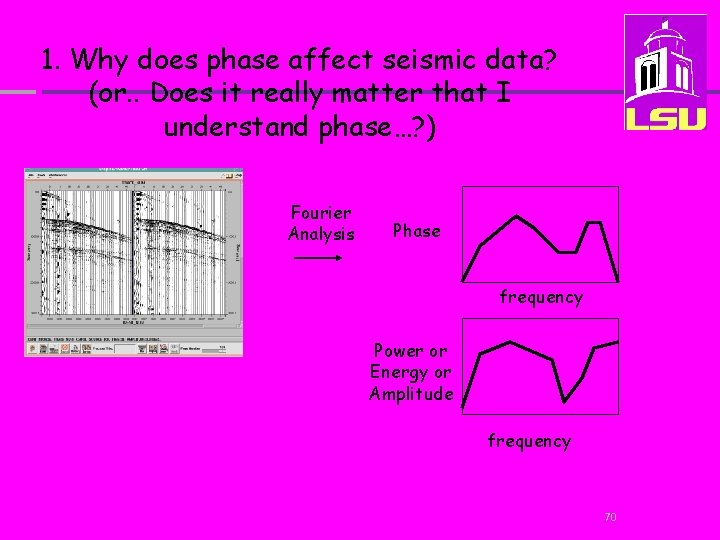
IMPORTANT QUESTIONS 1. Why does phase affect seismic data? (or. . Does it really matter that I understand phase…? ) 2. How do phase shifts affect seismic data? ( or. . . What does it do to my signal shape? 69

1. Why does phase affect seismic data? (or. . Does it really matter that I understand phase…? ) Fourier Analysis Phase frequency Power or Energy or Amplitude frequency 70

1. Why does phase affect seismic data? Signal processing through Fourier Decomposition breaks down seismic data into not only its frequency components (Real portion of the seismic data) but into the phase component (imaginary part). So, decomposed seismic data is complex. If you don’t know the phase you cannot get the data back into the time domain. When we bandpass filter we can choose to change the phase or keep it the same (default) Data is usually shot so that phase is as close to 0 for all frequencies. 71

IMPORTANT QUESTIONS 2. How do phase shifts affect seismic data? Let’s look at just one harmonic component of a complex signal is known as the phase A negative phase shift ADVANCES the signal and vice versa The cosine signal is delayed by 90 degrees with respect to a sine signal 72

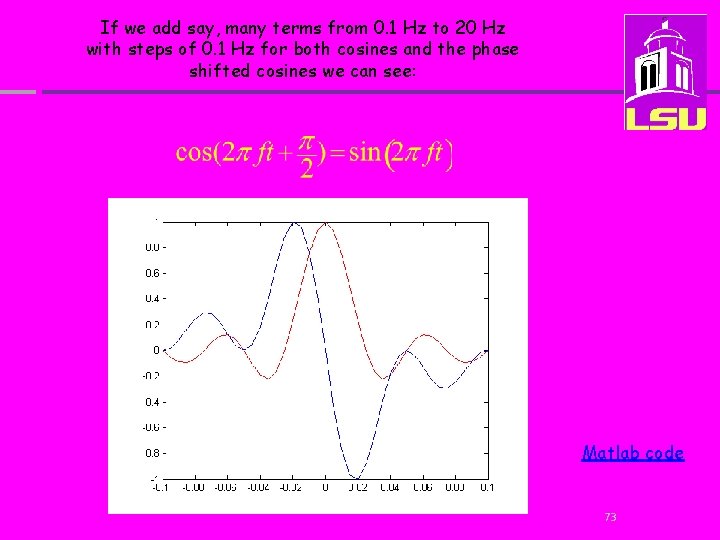
If we add say, many terms from 0. 1 Hz to 20 Hz with steps of 0. 1 Hz for both cosines and the phase shifted cosines we can see: Matlab code 73

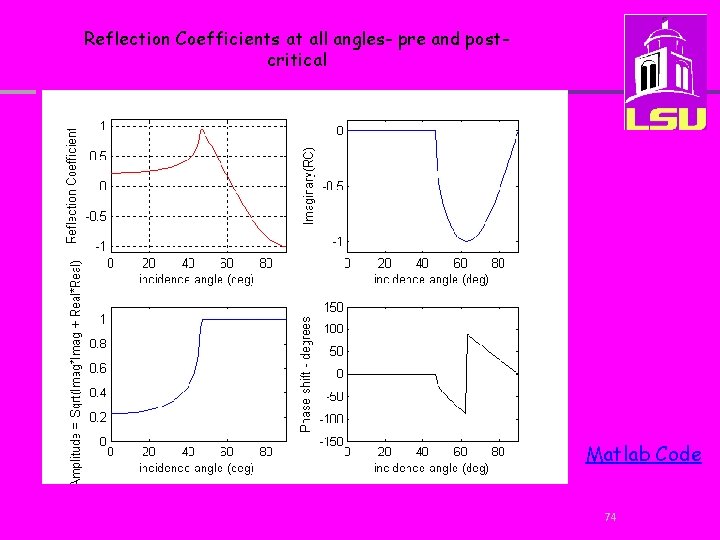
Reflection Coefficients at all angles- pre and postcritical Matlab Code 74

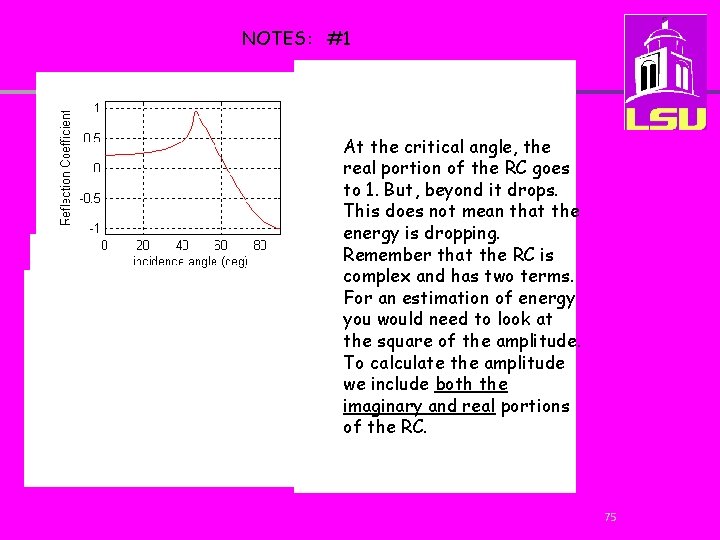
NOTES: #1 At the critical angle, the real portion of the RC goes to 1. But, beyond it drops. This does not mean that the energy is dropping. Remember that the RC is complex and has two terms. For an estimation of energy you would need to look at the square of the amplitude. To calculate the amplitude we include both the imaginary and real portions of the RC. 75

NOTES: #2 For the critical ray, amplitude is maximum (=1) at critical angle. Post-critical angles also have a maximum amplitude because all the energy is coming back as a reflected wave and no energy is getting into the lower layer 76

NOTES: #3 Post-critical angle rays will experience a phase shift, that is the shape of the signal will change. 77

Approximating reflection events with hyperbolic shapes We have seen that for a single-layer case: (rearranging equation 6) V 1 h 1 78

Approximating reflection events with hyperbolic shapes From Liner (2004; p. 92), for an n-layer case we have: h 1 h 2 h 3 h 4 For example, where n=3, after 6 refractions and 1 reflection 79 per ray we have the above scenario

Approximating reflection events with hyperbolic shapes Coefficients c 1, c 2, c 3 are given in terms of a second function set of coefficients, the a series, where a m is defined as follows: For example, in the case of a single layer we have: One-layer case (n=1) 80

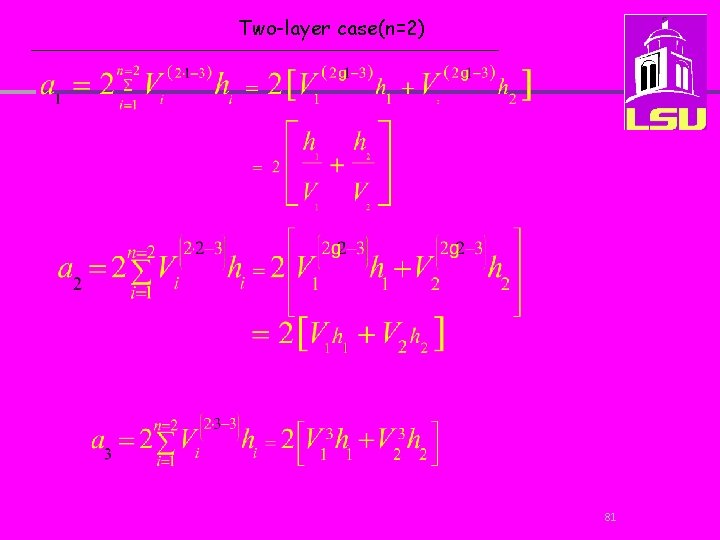
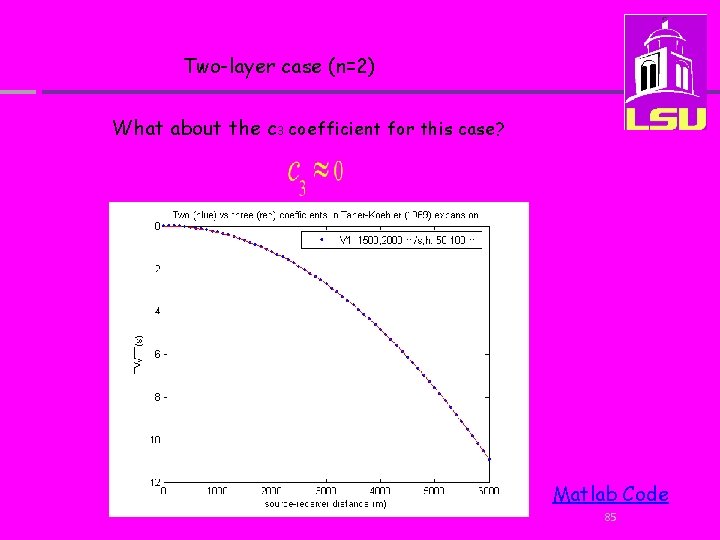
Two-layer case(n=2) 81

The “c” coefficients are defined in terms of combinations of the “a” function, so that: 82
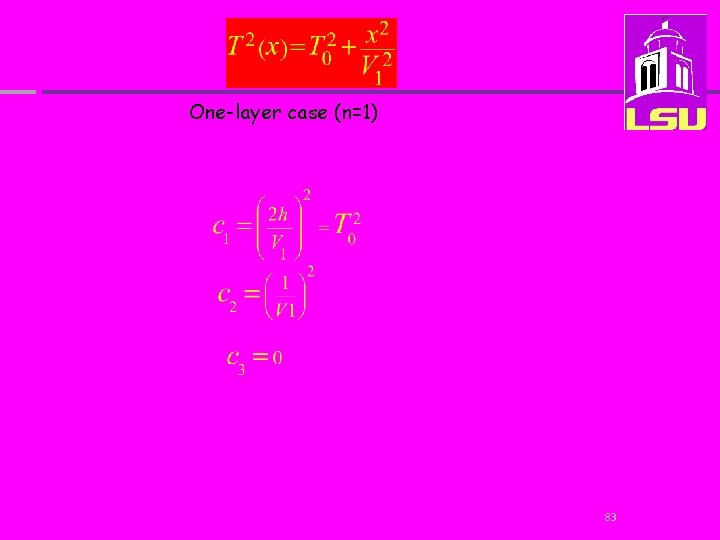
One-layer case (n=1) 83

Two-layer case (n=2) C 2=1/Vrms (See slide 14 of “Wave in Fluids”) 84

Two-layer case (n=2) What about the c 3 coefficient for this case? Matlab Code 85

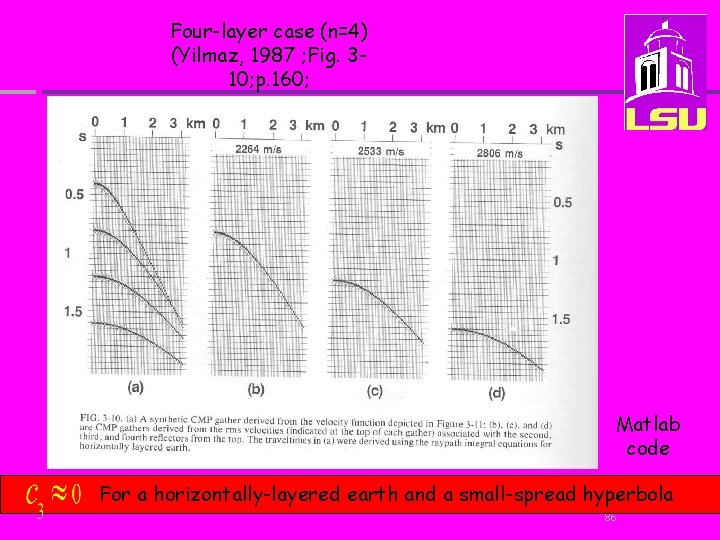
Four-layer case (n=4) (Yilmaz, 1987 ; Fig. 310; p. 160; Matlab code For a horizontally-layered earth and a small-spread hyperbola 86

87

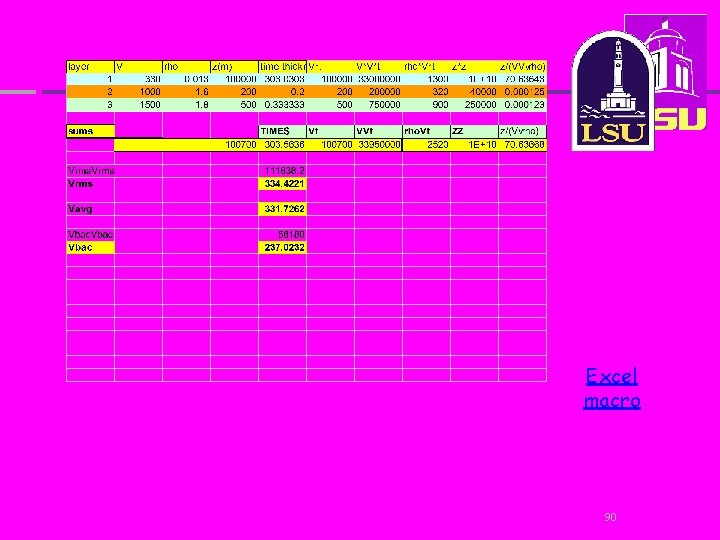
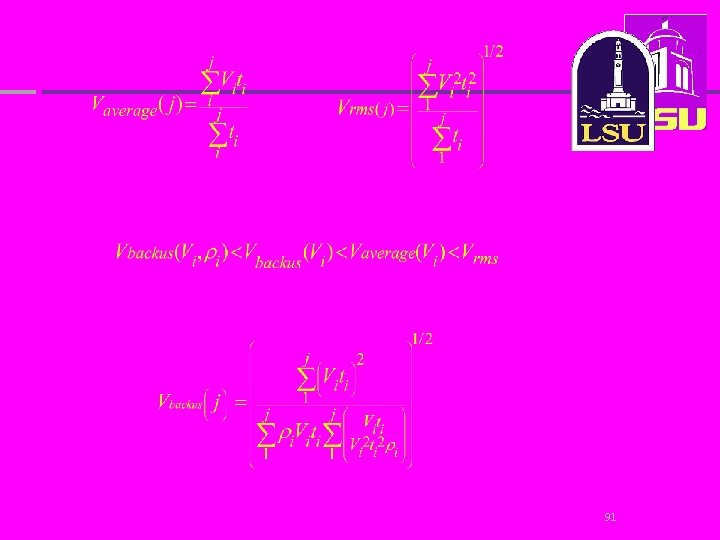
Mean velocity; traditional Very important for basic seismic processing. Can be obtained directly from seismic field data or GPR field data. Errors ~10% 88

V=330 m/s, rho =0 i=1 z=100000 m s = 200 m; V=1000 m/s, rho =1. 6 i=2 V=1500 m/s, z= 500 m rho =1. 8 i=3=j 89

Excel macro 90

91
 Half empty or half full
Half empty or half full Clock in quarters
Clock in quarters Past and to
Past and to Half third quarter
Half third quarter Of an hour is a quarter of the clock face
Of an hour is a quarter of the clock face Quarter 3 time
Quarter 3 time Quarter turn half turn
Quarter turn half turn Joy luck club discussion questions by chapter
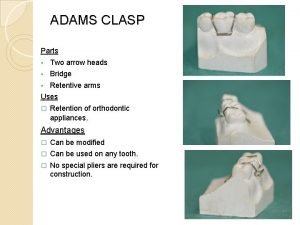
Joy luck club discussion questions by chapter Retentive clasp arm
Retentive clasp arm Bar type clasp
Bar type clasp Half-section
Half-section Difference between full wave and half wave rectifier
Difference between full wave and half wave rectifier Rectifier example
Rectifier example Half strength darrow's solution composition
Half strength darrow's solution composition Half colours meaning
Half colours meaning How to make a sandwich paragraph
How to make a sandwich paragraph Hybrid mythological creatures
Hybrid mythological creatures What is a half horse half man called
What is a half horse half man called What is a myth
What is a myth Delphi
Delphi Mulciber roman god
Mulciber roman god Softirq vs tasklet
Softirq vs tasklet Narnia half mens half geit
Narnia half mens half geit Gerald croft
Gerald croft Half duplex vs full duplex
Half duplex vs full duplex Full wave rectifier vs half wave rectifier
Full wave rectifier vs half wave rectifier Full width at half maximum
Full width at half maximum Half vs full duplex
Half vs full duplex Half a day point of view
Half a day point of view Ethernet full duplex vs half duplex
Ethernet full duplex vs half duplex Topic outline example
Topic outline example Perimeter of a quadrant formula
Perimeter of a quadrant formula Reading and writing quarter 3
Reading and writing quarter 3 Disadvantages of rift sawn
Disadvantages of rift sawn What is this time
What is this time A quarter pass 8
A quarter pass 8 Whats a quarter past 12
Whats a quarter past 12 Clock with missing numbers
Clock with missing numbers Welcome 2nd quarter
Welcome 2nd quarter Welcome to quarter 2
Welcome to quarter 2 It's a quarter to two
It's a quarter to two Clock showing 4:55
Clock showing 4:55 Clock in quarters
Clock in quarters Tdes school
Tdes school Qbr presentation template
Qbr presentation template Principles of marketing quarter 2 module 9
Principles of marketing quarter 2 module 9 Principles of marketing quarter 2 -- module 7
Principles of marketing quarter 2 -- module 7 Principles of marketing module
Principles of marketing module Reverse three-quarter crown
Reverse three-quarter crown Partial veneer crown indications
Partial veneer crown indications Define gibbous moon
Define gibbous moon Quarter turn belt drive
Quarter turn belt drive Rope drive pulley
Rope drive pulley Quarter inch fraction
Quarter inch fraction Even symmetry fourier series
Even symmetry fourier series English 5 week 6
English 5 week 6 Which best explains why the moon has phases?
Which best explains why the moon has phases? Quarters
Quarters Perimeter formula for quarter circle
Perimeter formula for quarter circle Inertia
Inertia Quarter wave transformer smith chart
Quarter wave transformer smith chart It's twenty to nine
It's twenty to nine Welcome to quarter 3
Welcome to quarter 3 Cultural industries quarter sheffield
Cultural industries quarter sheffield English 9 quarter 2 week 3
English 9 quarter 2 week 3 Quarter wave transformer
Quarter wave transformer Volume of a half cylinder
Volume of a half cylinder Jones matrix for half wave plate
Jones matrix for half wave plate Gross earnings formula business math
Gross earnings formula business math Negative quarter power scaling
Negative quarter power scaling It's a half past six
It's a half past six Cal poly quarter or semester
Cal poly quarter or semester Xe6s24f145d10 element
Xe6s24f145d10 element Quarter moon
Quarter moon Quarter moon
Quarter moon Three quarter floating rear axle
Three quarter floating rear axle A crane lowers a girder into place
A crane lowers a girder into place Quarter moon
Quarter moon Quarter moon
Quarter moon Quarter moon
Quarter moon Exadata quarter rack
Exadata quarter rack The head of the virgin in three-quarter view facing right
The head of the virgin in three-quarter view facing right Aqha uk
Aqha uk Smepa 1st quarter
Smepa 1st quarter Length of bridge in adams clasp
Length of bridge in adams clasp Half past 11
Half past 11 Quarter rest definition
Quarter rest definition Principles of marketing
Principles of marketing First quarter moon gif
First quarter moon gif Mid quarter test
Mid quarter test Quarter turn belt drive
Quarter turn belt drive It's quarter past one
It's quarter past one