Leader Election in Rings 1 A Ring Network

Leader Election in Rings 1

A Ring Network 2

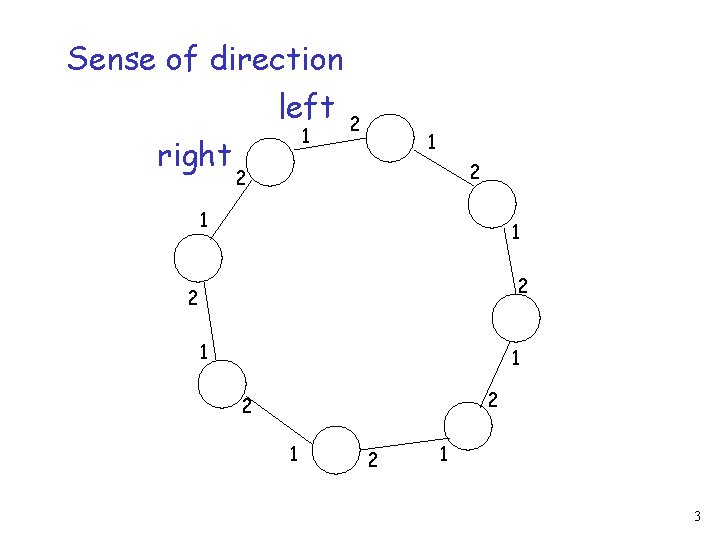
Sense of direction left 2 right 1 1 2 2 1 3

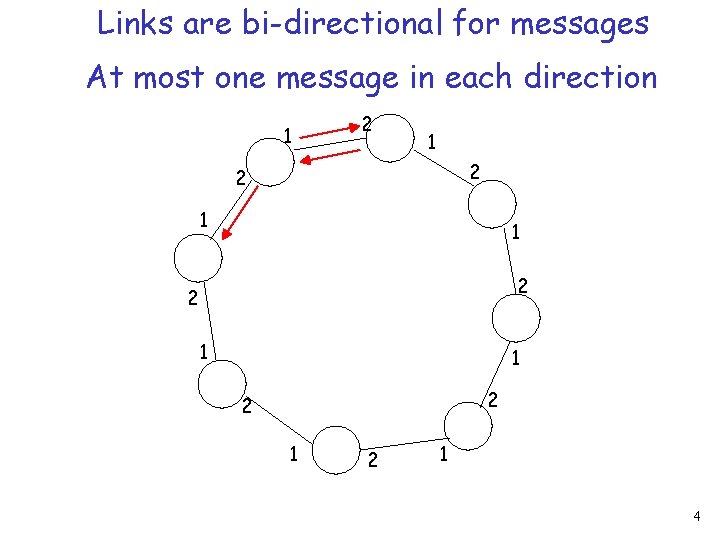
Links are bi-directional for messages At most one message in each direction 1 2 2 1 4

Anonymous Ring 1 2 2 1 5

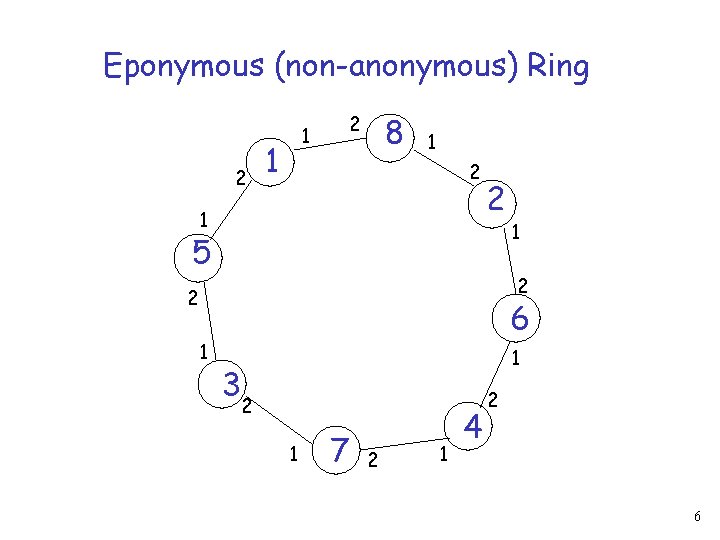
Eponymous (non-anonymous) Ring 2 1 1 2 8 1 2 5 2 2 1 1 6 1 3 2 1 7 2 1 4 2 6

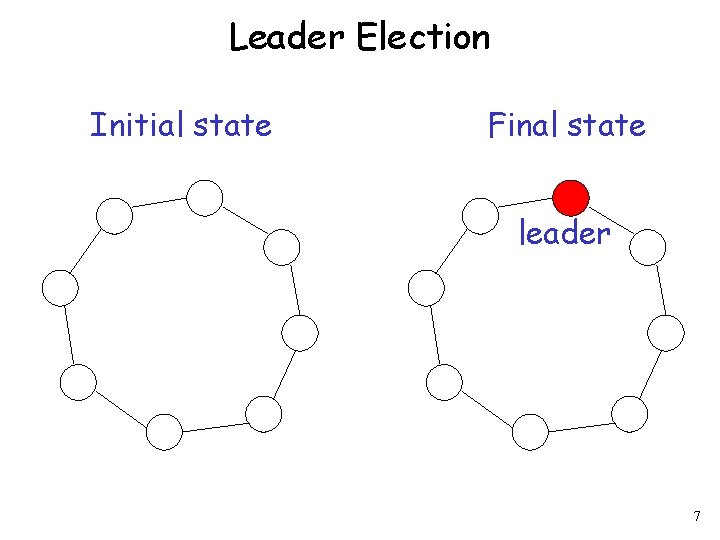
Leader Election Initial state Final state leader 7

Leader election algorithms are affected by: Anonymous Ring Eponymous Ring The size of the network Synchronous Algorithm Asynchronous Algorithm is known is not known 8

Synchronous Anonymous Rings Every processor runs the same algorithm Every processor does exactly the same execution 9

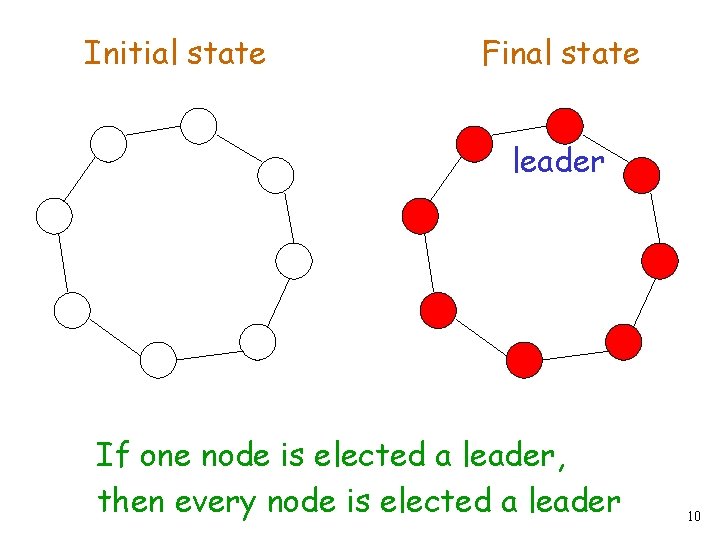
Initial state Final state leader If one node is elected a leader, then every node is elected a leader 10

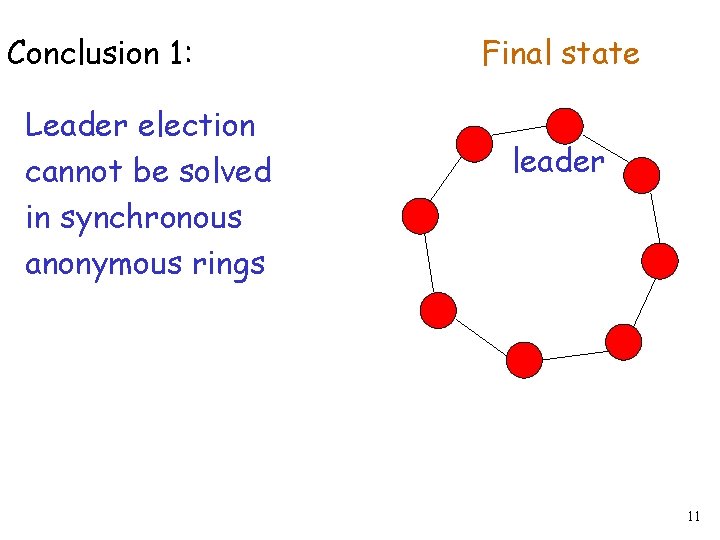
Conclusion 1: Leader election cannot be solved in synchronous anonymous rings Final state leader 11

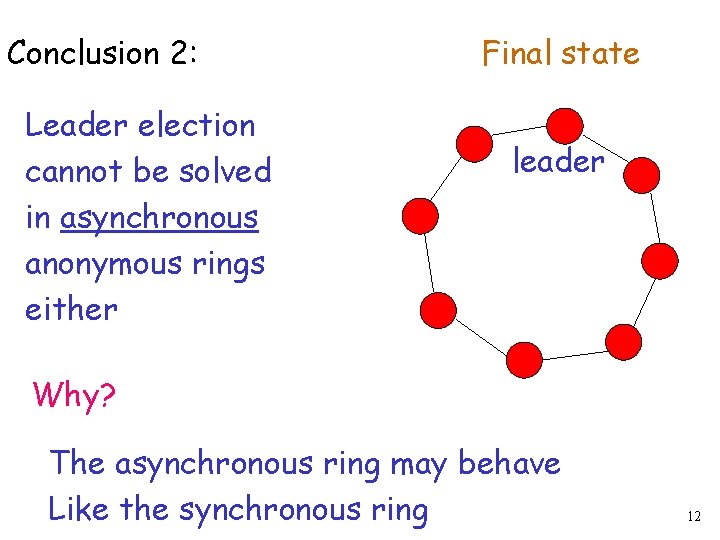
Conclusion 2: Leader election cannot be solved in asynchronous anonymous rings either Final state leader Why? The asynchronous ring may behave Like the synchronous ring 12

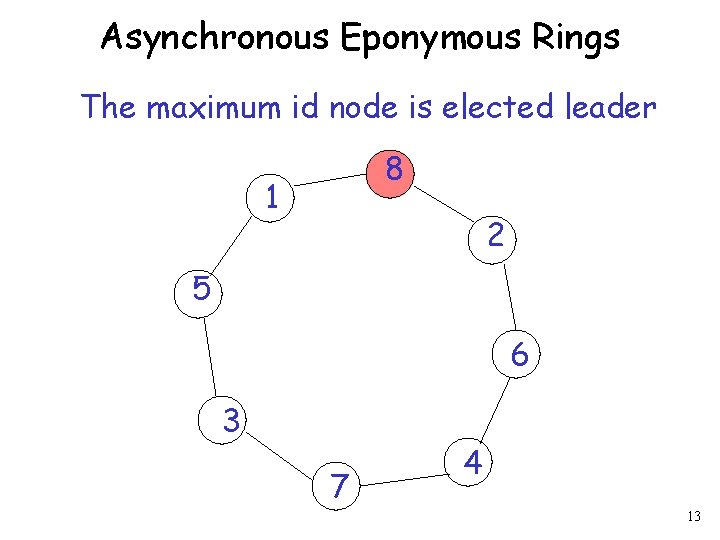
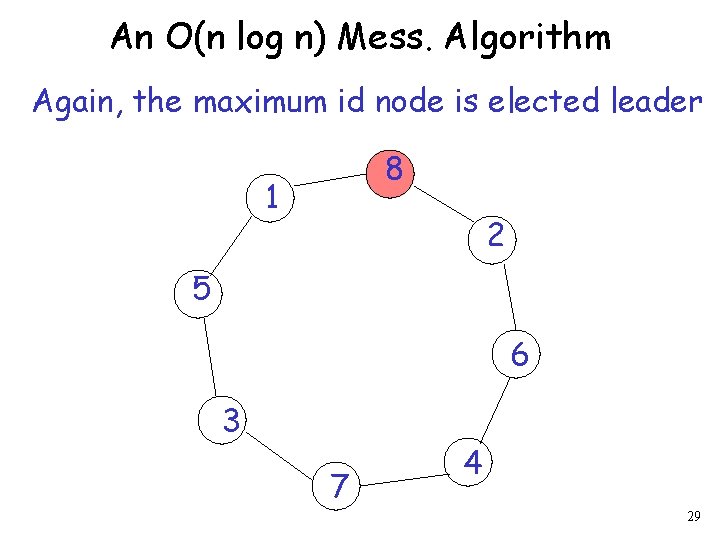
Asynchronous Eponymous Rings The maximum id node is elected leader 8 1 2 5 6 3 7 4 13

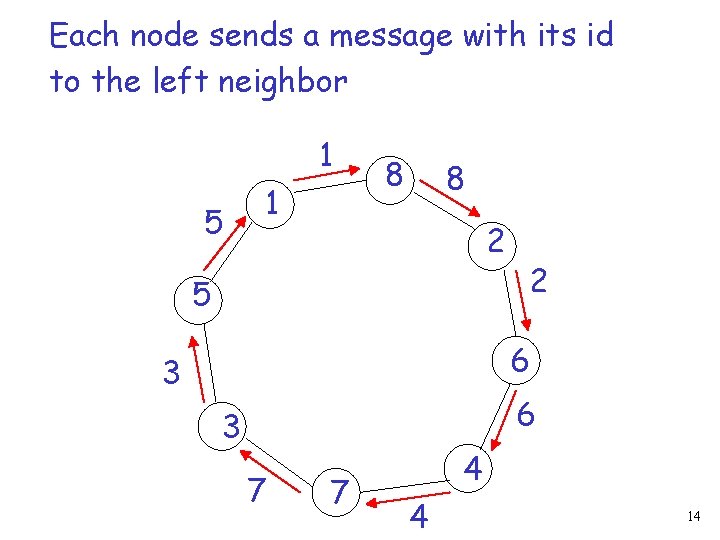
Each node sends a message with its id to the left neighbor 1 5 1 8 8 2 5 2 6 3 7 7 4 4 14

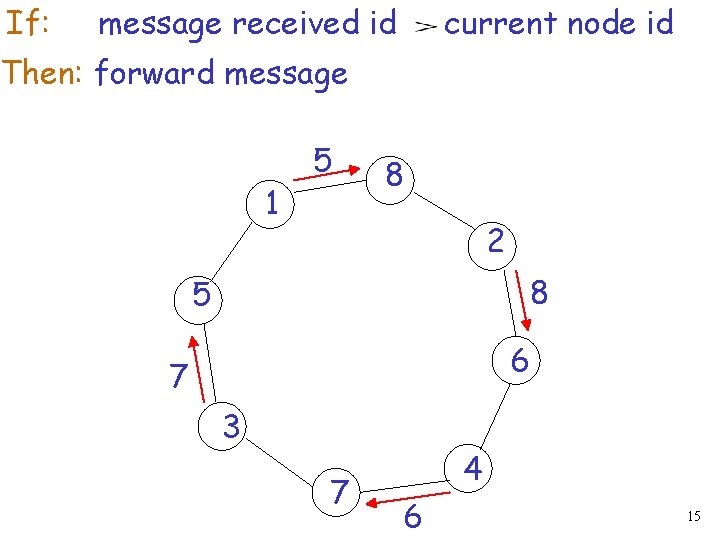
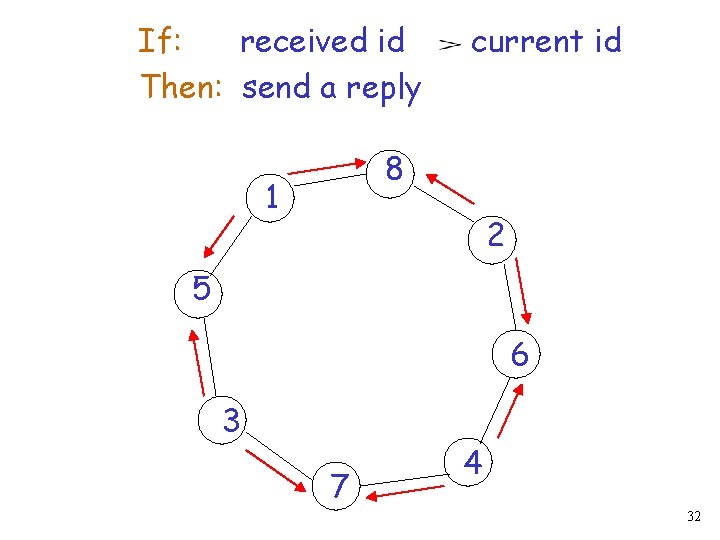
If: message received id current node id Then: forward message 1 5 8 2 8 5 6 7 3 7 4 6 15

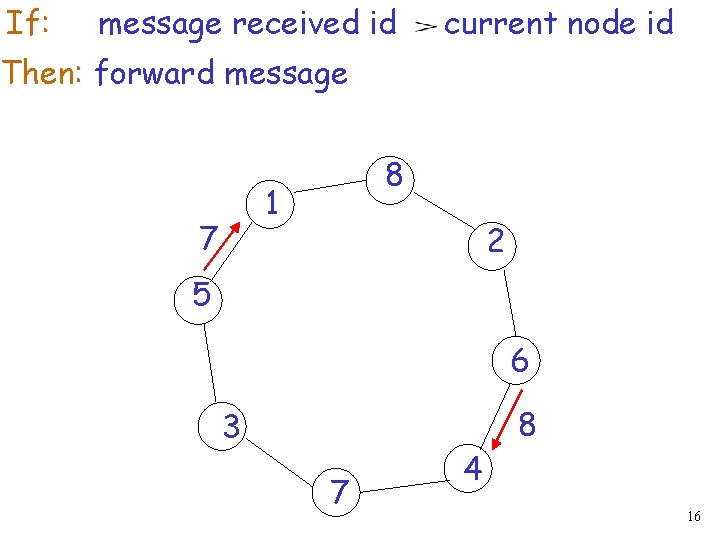
If: message received id current node id Then: forward message 8 1 7 2 5 6 3 7 4 8 16

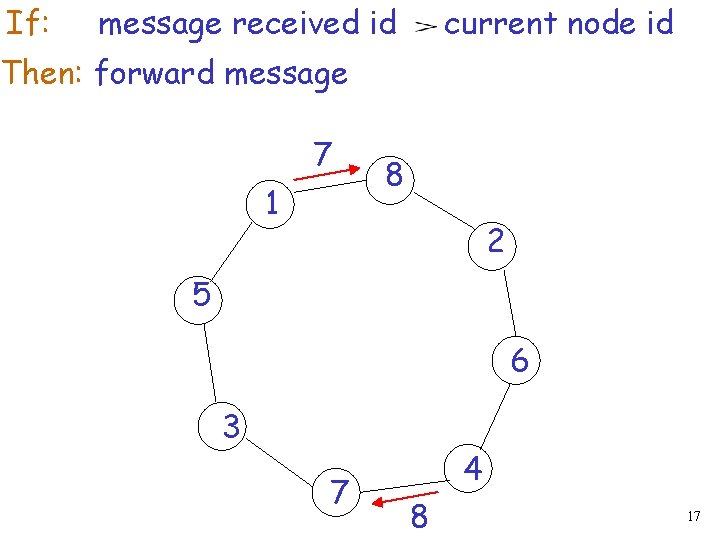
If: message received id current node id Then: forward message 7 1 8 2 5 6 3 7 4 8 17

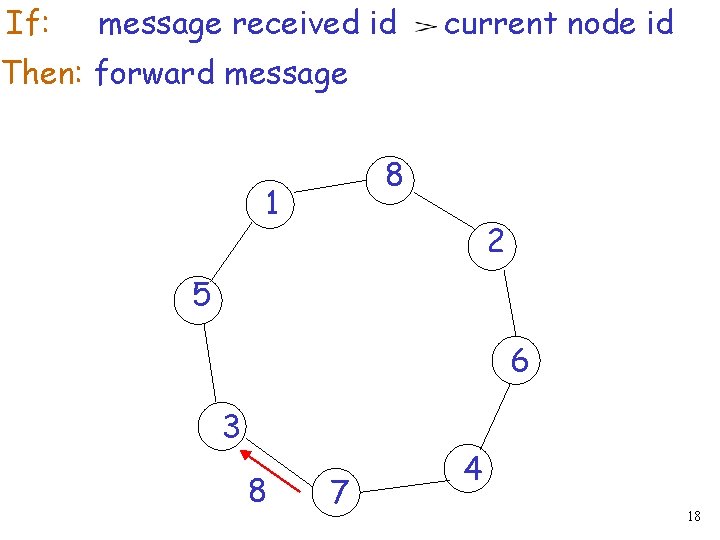
If: message received id current node id Then: forward message 8 1 2 5 6 3 8 7 4 18

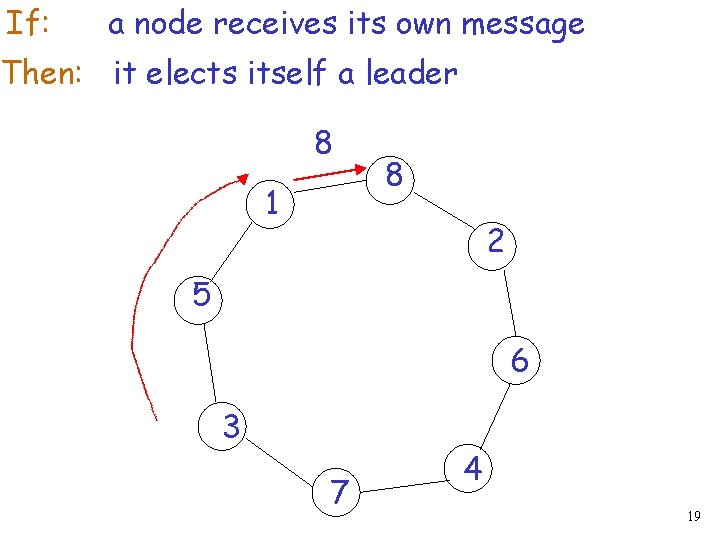
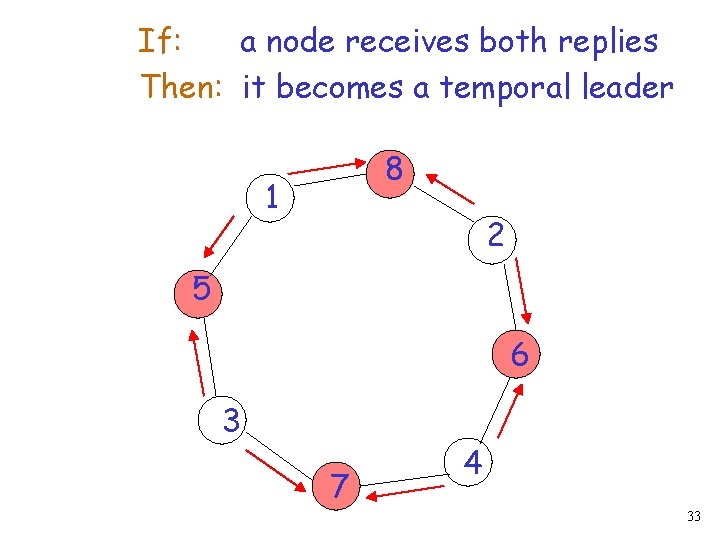
If: a node receives its own message Then: it elects itself a leader 8 1 8 2 5 6 3 7 4 19

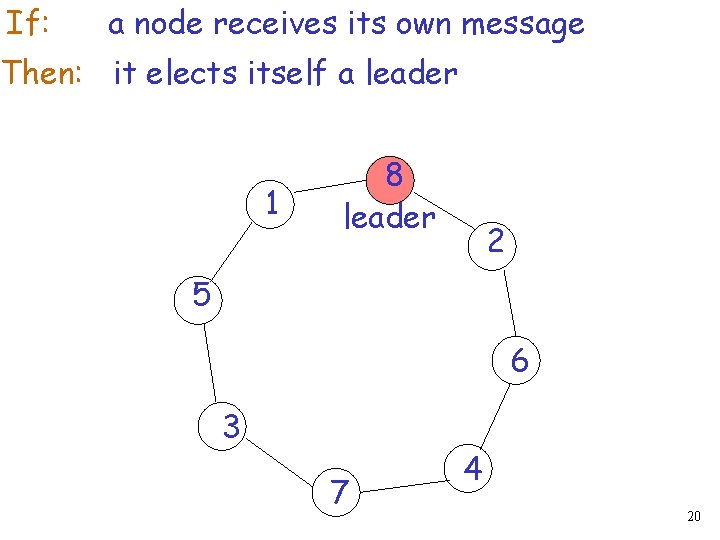
If: a node receives its own message Then: it elects itself a leader 1 8 leader 2 5 6 3 7 4 20

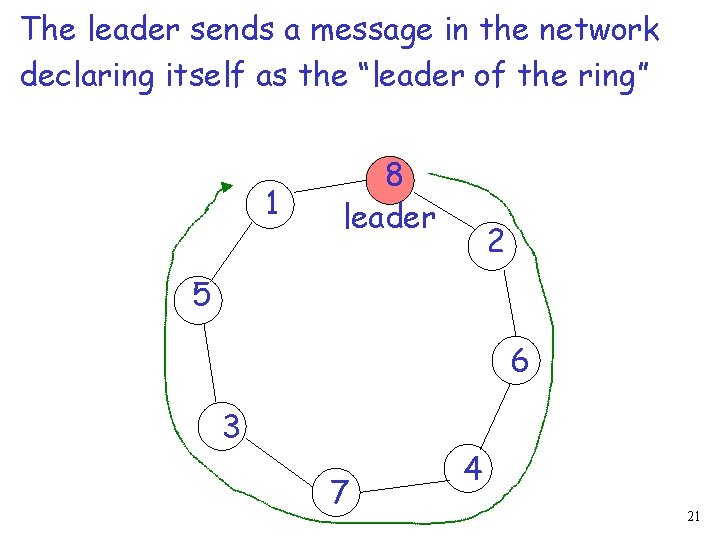
The leader sends a message in the network declaring itself as the “leader of the ring” 1 8 leader 2 5 6 3 7 4 21

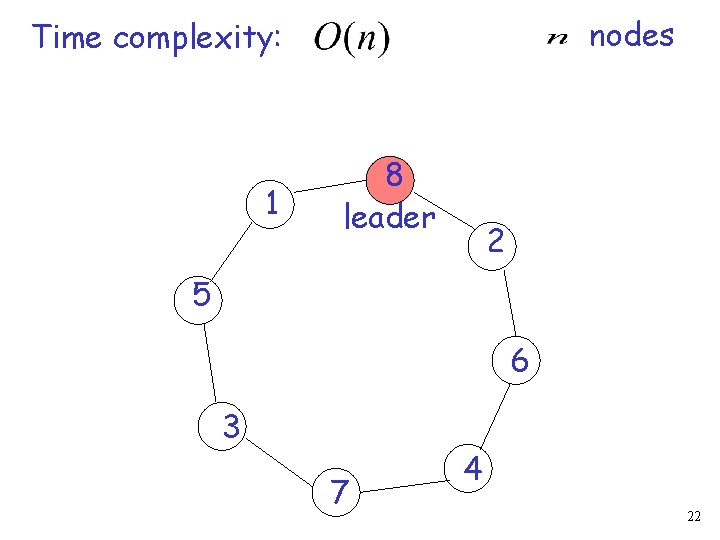
nodes Time complexity: 1 8 leader 2 5 6 3 7 4 22

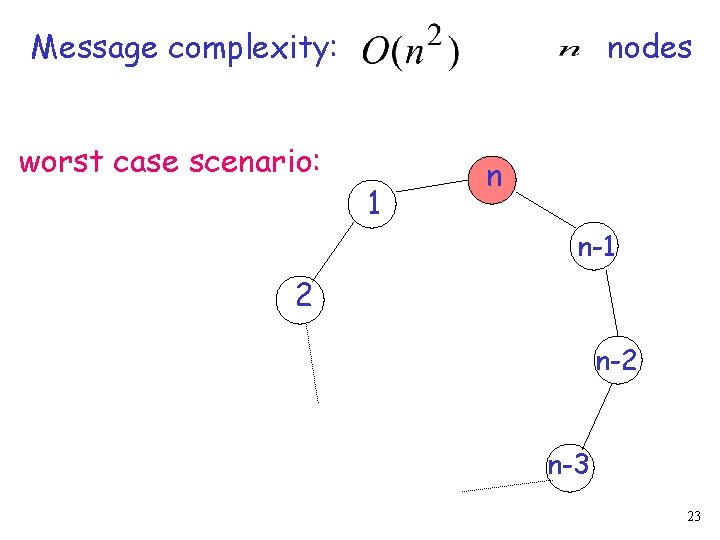
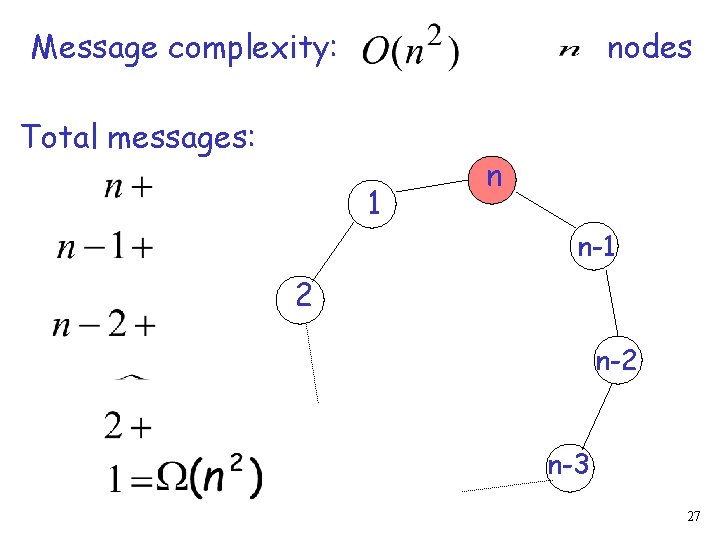
Message complexity: worst case scenario: nodes 1 n n-1 2 n-3 23

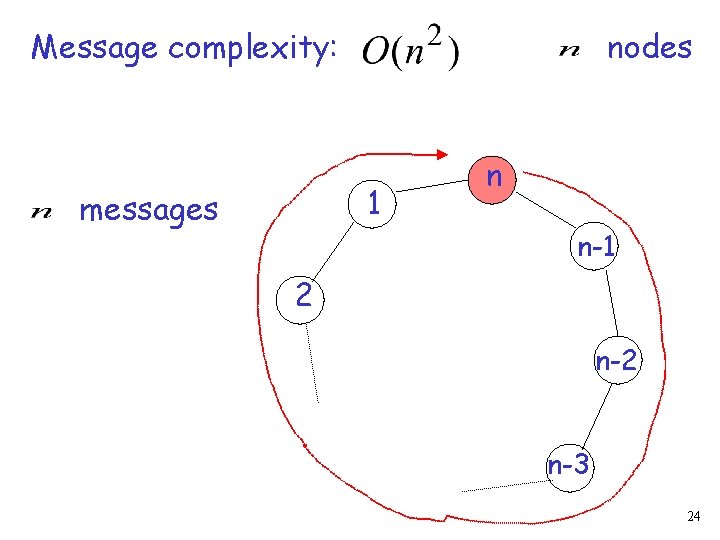
Message complexity: nodes 1 messages n n-1 2 n-3 24

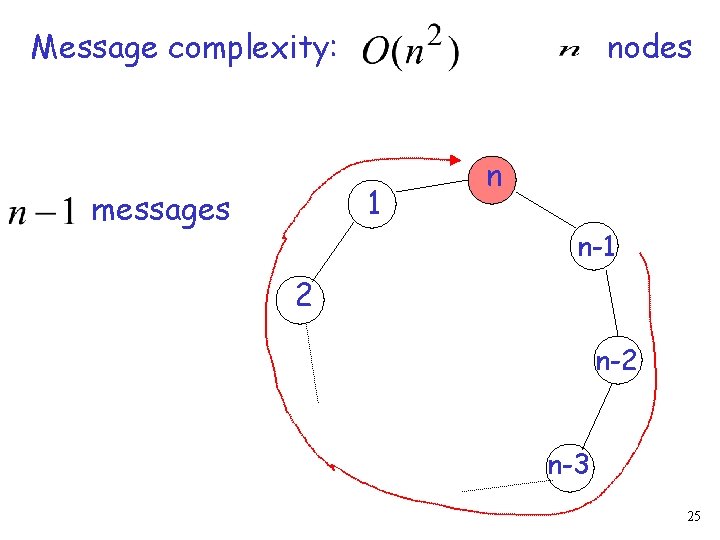
Message complexity: nodes 1 messages n n-1 2 n-3 25

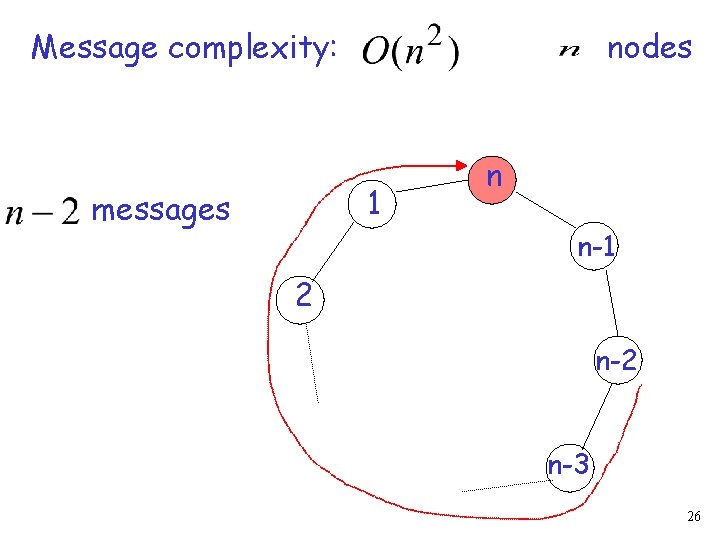
Message complexity: nodes 1 messages n n-1 2 n-3 26

Message complexity: nodes Total messages: 1 n n-1 2 n-3 27

Notes: does not need to be known to the algorithm The algorithm can be converted to asynchronous 28

An O(n log n) Mess. Algorithm Again, the maximum id node is elected leader 8 1 2 5 6 3 7 4 29

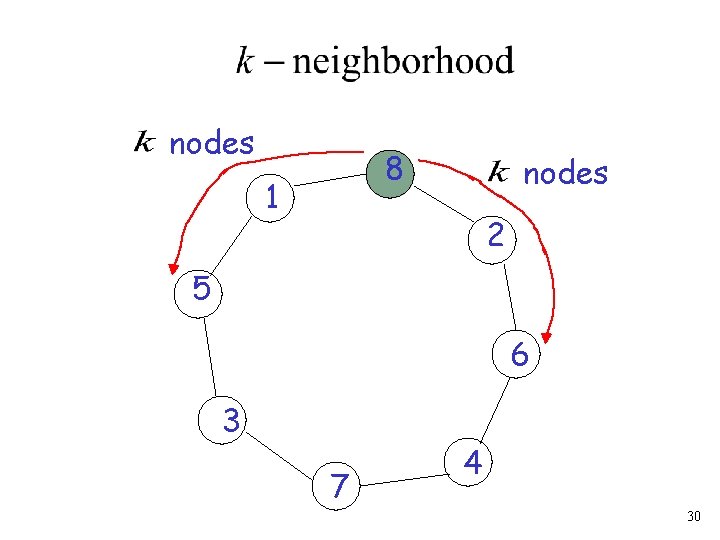
nodes 8 1 nodes 2 5 6 3 7 4 30

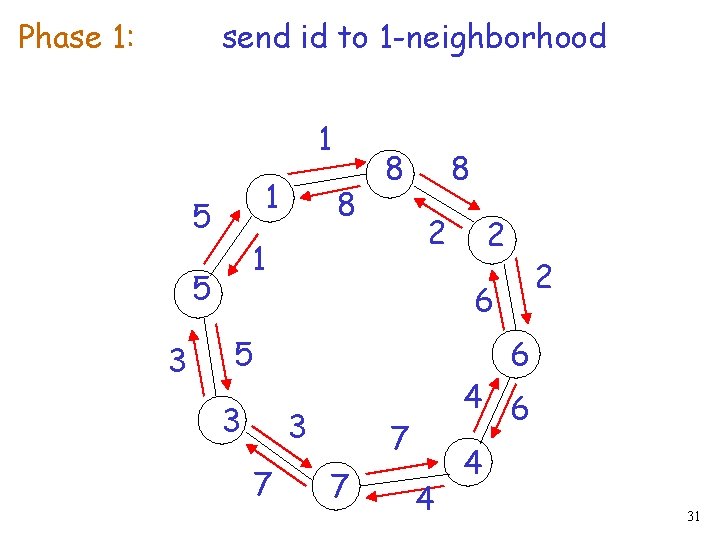
Phase 1: send id to 1 -neighborhood 1 1 5 8 2 1 5 3 8 8 6 3 7 2 6 5 3 2 4 6 7 7 4 4 31

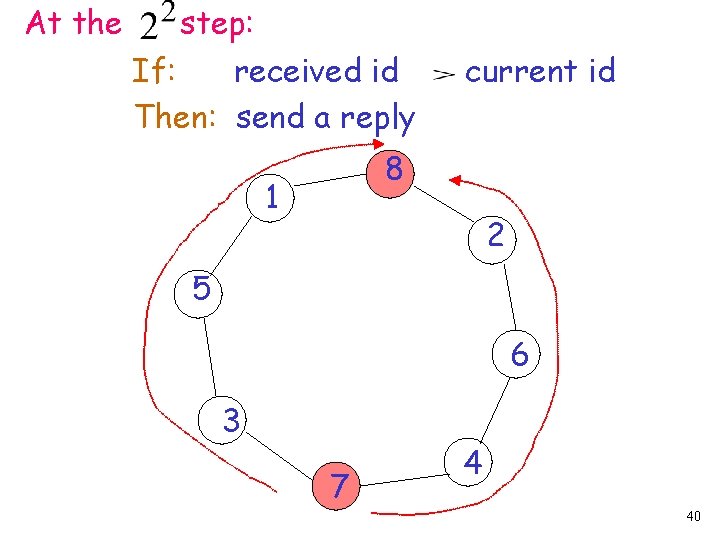
If: received id Then: send a reply current id 8 1 2 5 6 3 7 4 32

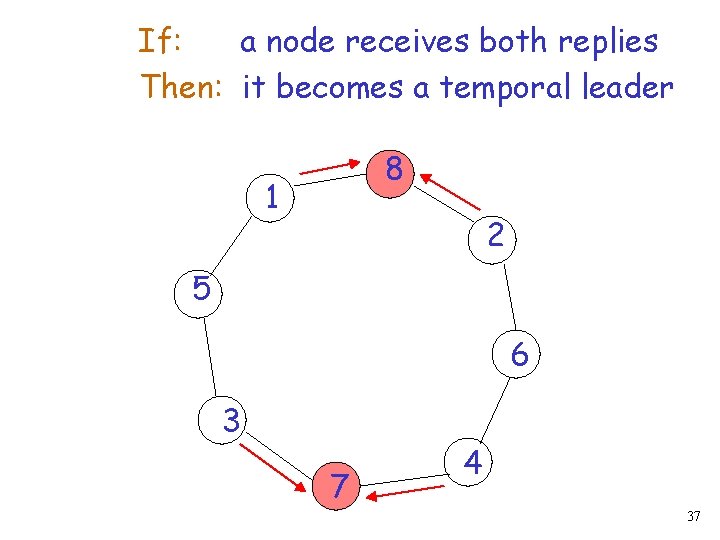
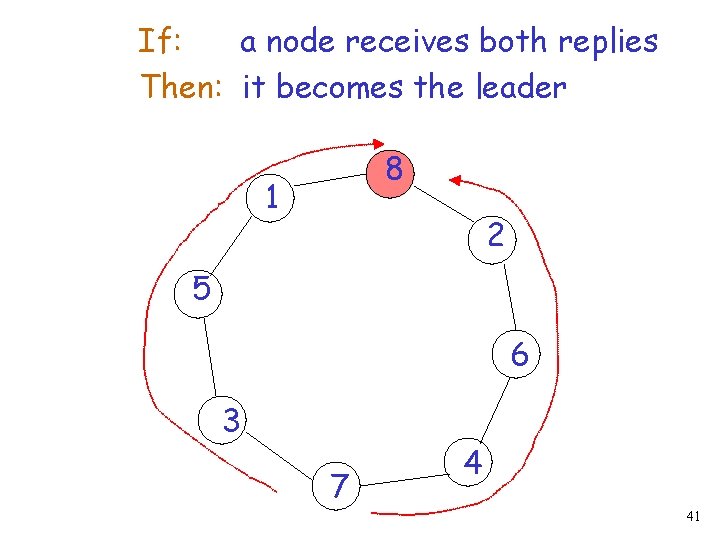
If: a node receives both replies Then: it becomes a temporal leader 8 1 2 5 6 3 7 4 33

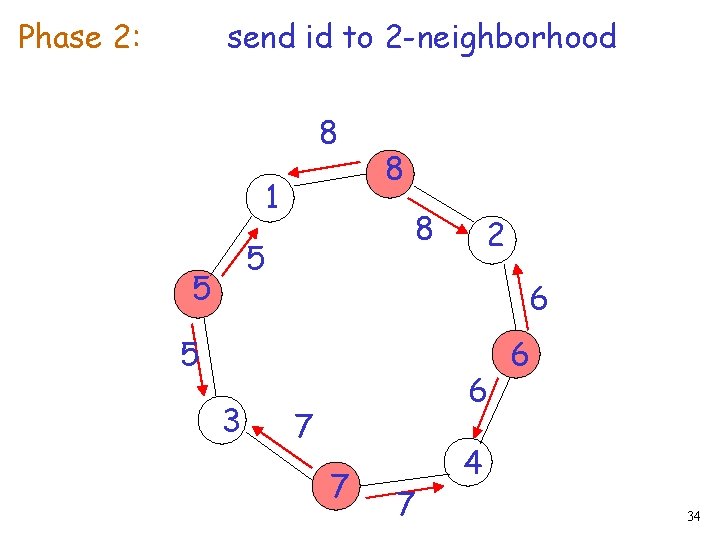
Phase 2: send id to 2 -neighborhood 8 1 8 5 5 8 6 5 3 2 6 7 7 7 6 4 34

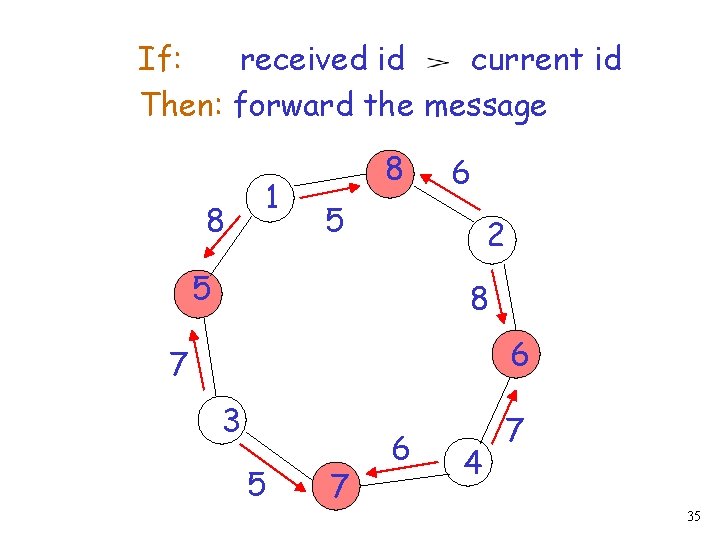
If: received id current id Then: forward the message 8 1 8 6 5 2 5 8 6 7 3 5 7 6 4 7 35

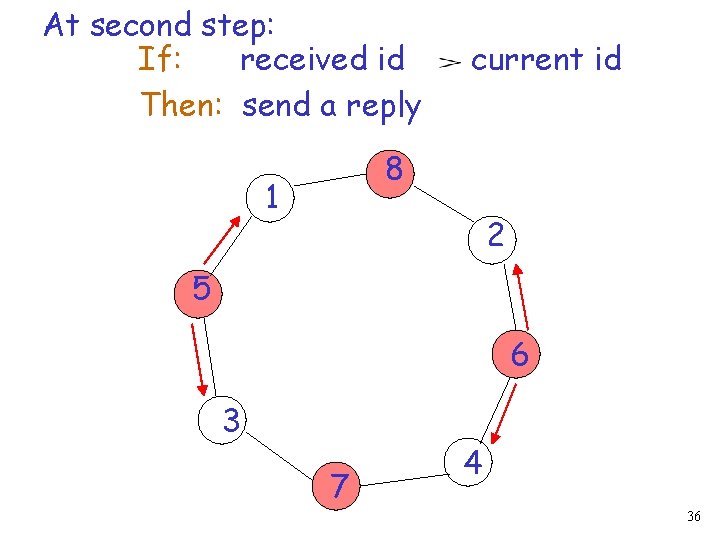
At second step: If: received id Then: send a reply current id 8 1 2 5 6 3 7 4 36

If: a node receives both replies Then: it becomes a temporal leader 8 1 2 5 6 3 7 4 37

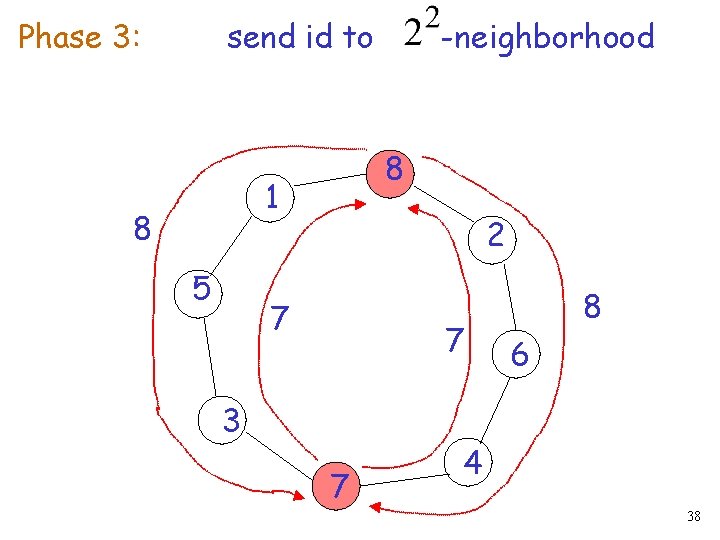
Phase 3: send id to 8 1 8 5 -neighborhood 2 7 7 3 7 8 6 4 38

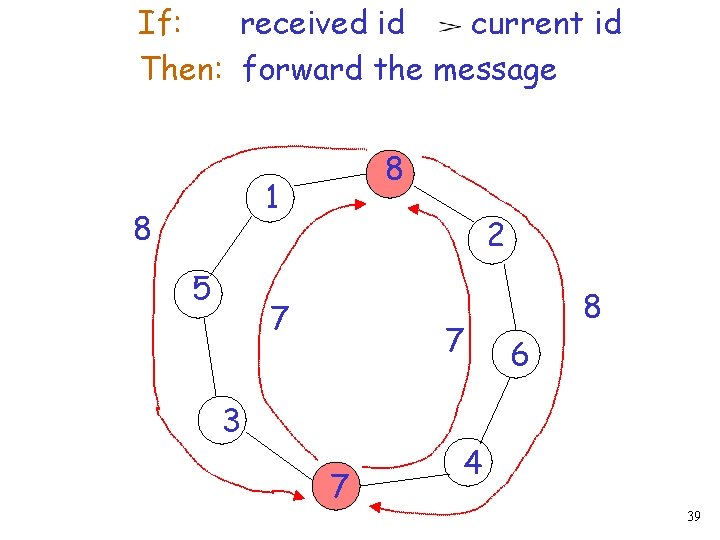
If: received id current id Then: forward the message 8 1 8 5 2 7 7 3 7 8 6 4 39

At the step: If: received id Then: send a reply current id 8 1 2 5 6 3 7 4 40

If: a node receives both replies Then: it becomes the leader 8 1 2 5 6 3 7 4 41

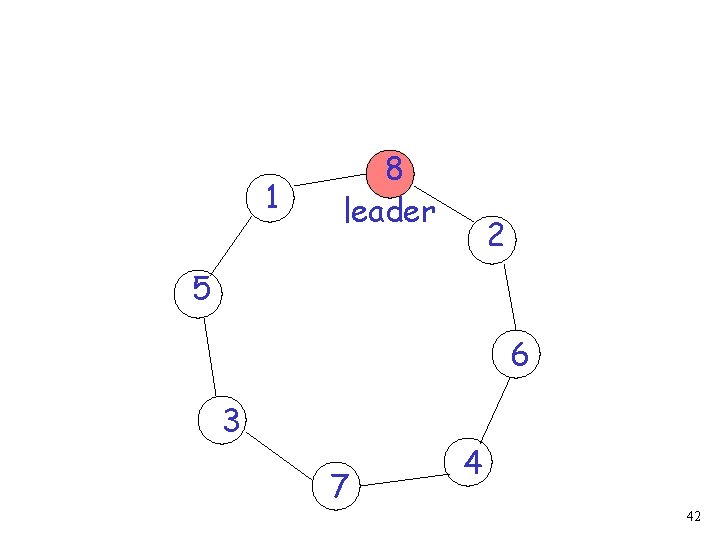
1 8 leader 2 5 6 3 7 4 42

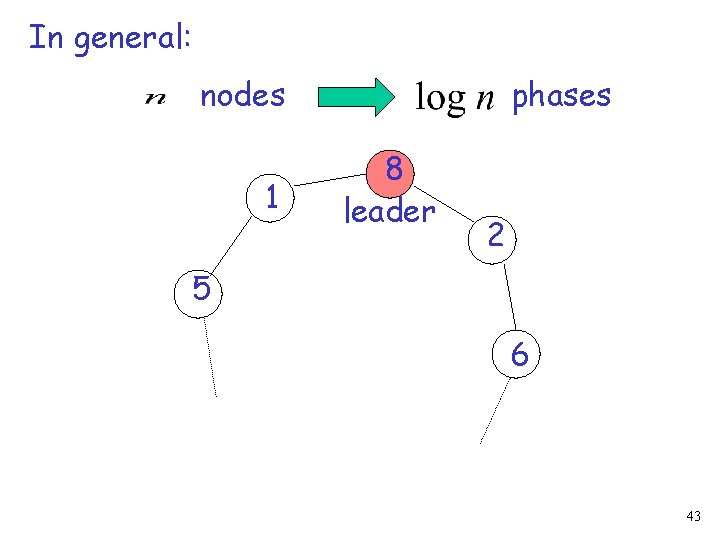
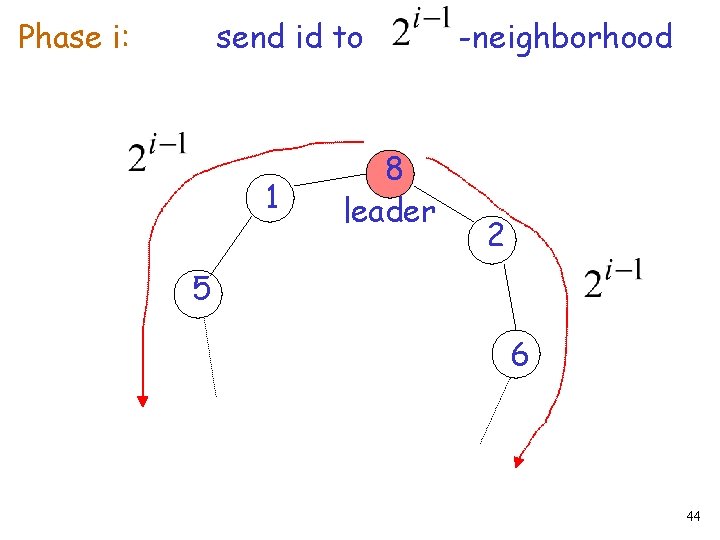
In general: nodes 1 phases 8 leader 2 5 6 43

Phase i: send id to 1 8 leader -neighborhood 2 5 6 44

Time complexity The leader spends time in Phase 1: 2 Phase 2: 4 … Phase i: … Phase log n: Total time: 45

Message complexity Messages per leader Max #leaders Phase 1: 4 Phase 2: 8 … Phase i: … Phase log n: 46

Messages per leader Max #leaders Phase 1: 4 Phase 2: 8 … Phase i: … Phase log n: Total messages: 47

Notes: The algorithm does not need to know It can be converted to an asynchronous algorithm 48

An Mess. Synchronous Algorithm is known The node with smallest id is elected leader There are rounds: If in round there is a node with id • this is the new leader • the algorithm terminates 49

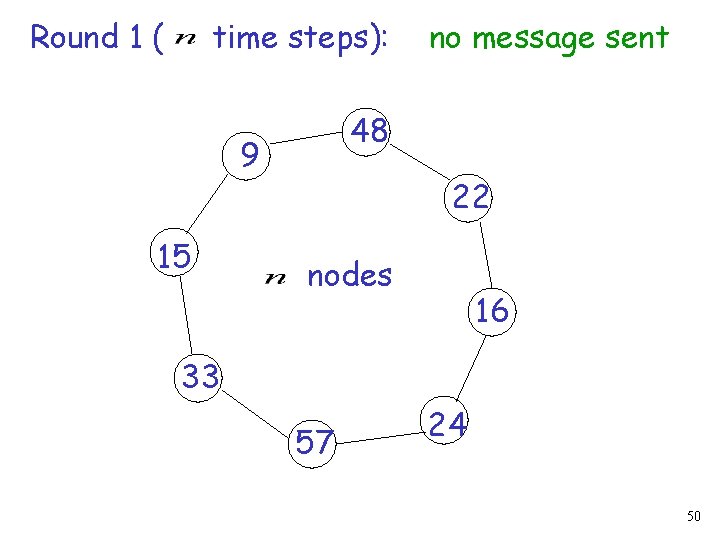
Round 1 ( time steps): 48 9 15 no message sent 22 nodes 16 33 57 24 50

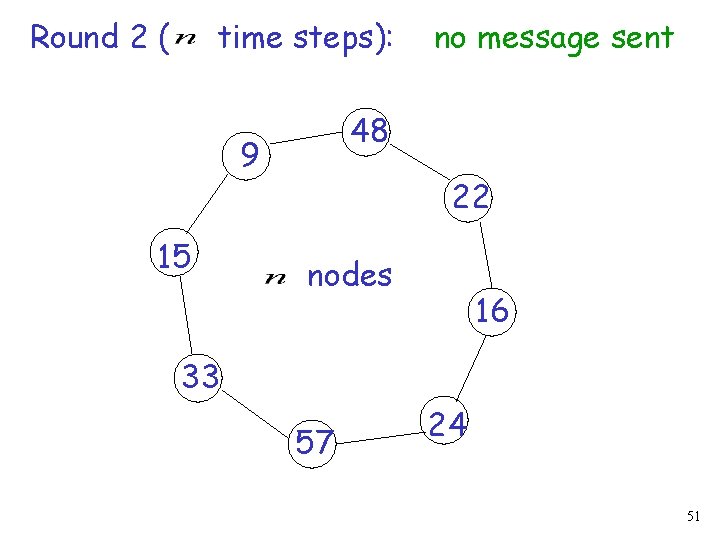
Round 2 ( time steps): 48 9 15 no message sent 22 nodes 16 33 57 24 51

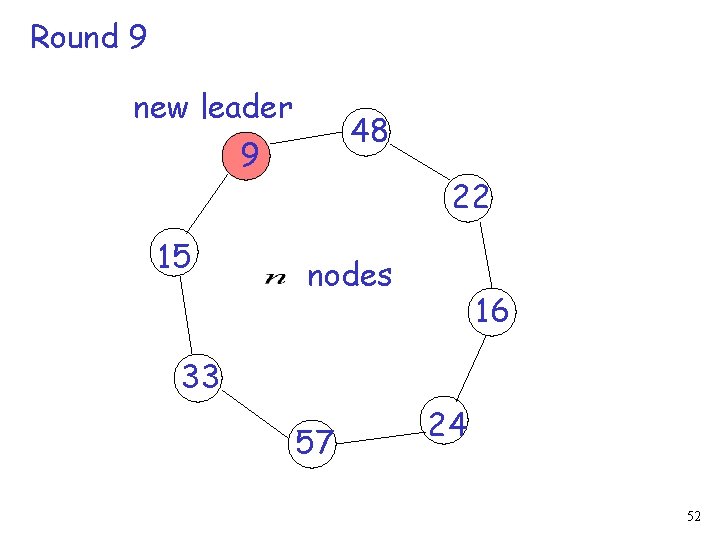
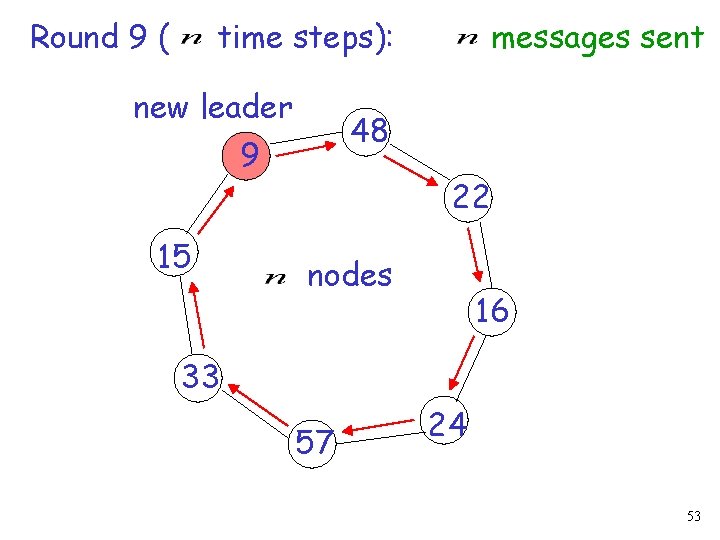
Round 9 new leader 48 9 15 22 nodes 16 33 57 24 52

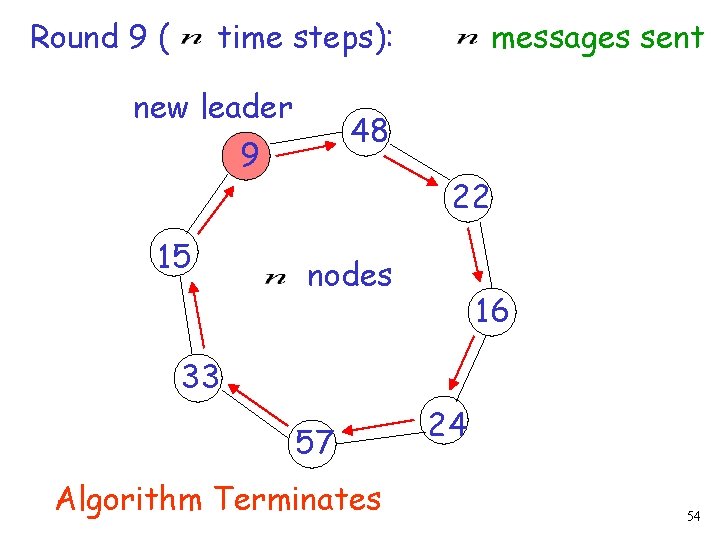
Round 9 ( time steps): new leader 48 9 15 messages sent 22 nodes 16 33 57 24 53

Round 9 ( time steps): new leader 48 9 15 messages sent 22 nodes 16 33 57 Algorithm Terminates 24 54

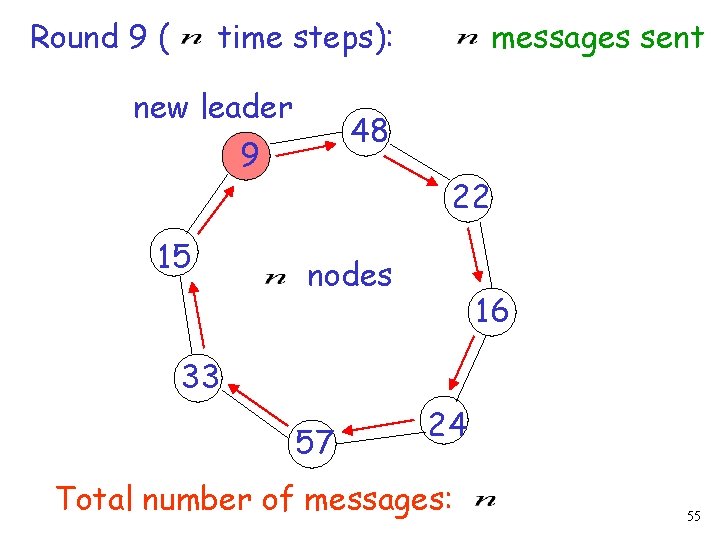
Round 9 ( time steps): new leader 48 9 15 messages sent 22 nodes 16 33 57 24 Total number of messages: 55

Another Synchronous Algorithm is not known The node with smallest id is elected leader 56

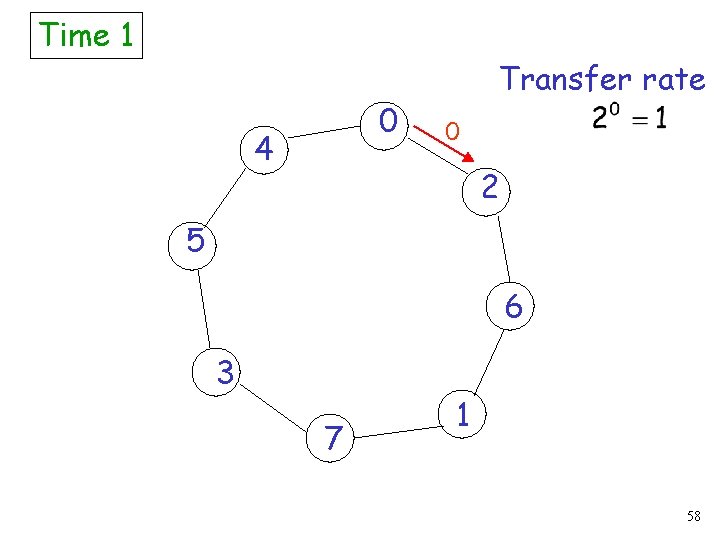
The algorithm: • Each node injects a message with its id • Message with id is injected and transferred with rate • Nodes which have seen smaller id absorb higher id messages 57

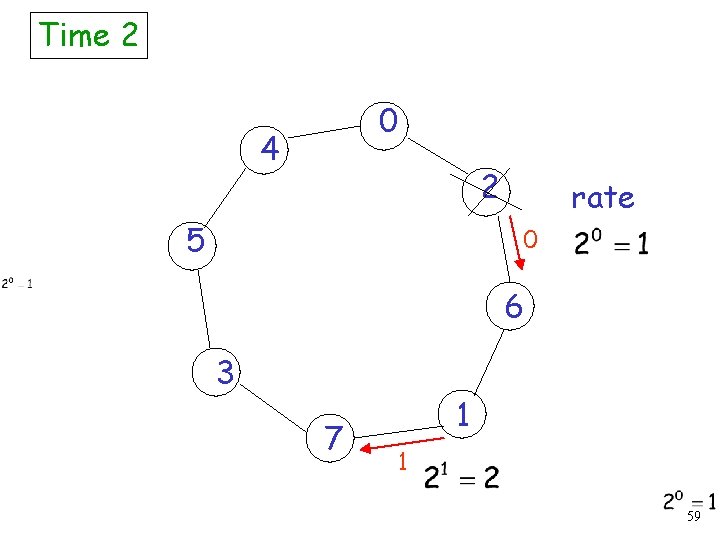
Time 1 0 4 Transfer rate 0 2 5 6 3 7 1 58

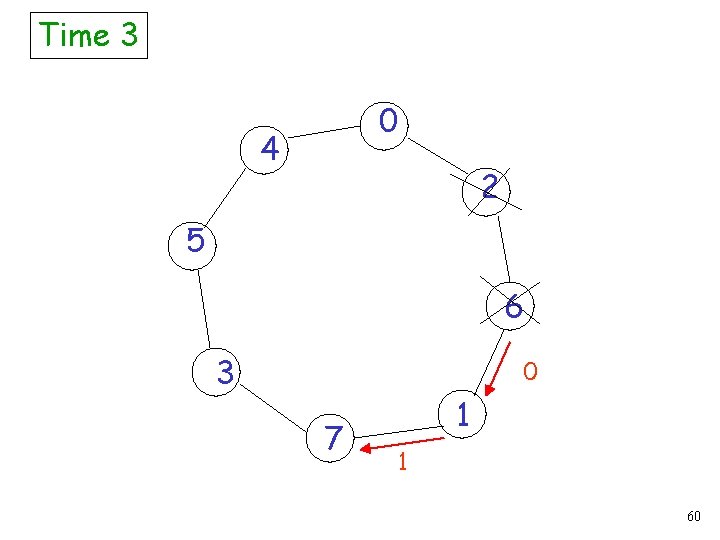
Time 2 0 4 2 5 rate 0 6 3 7 1 1 59

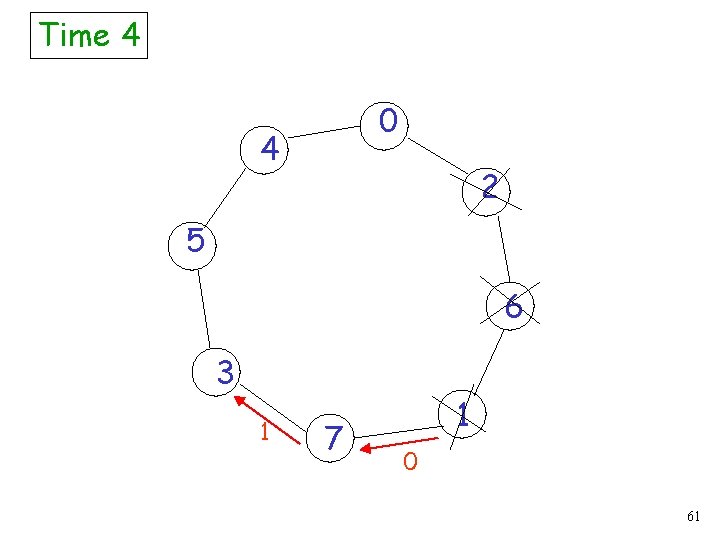
Time 3 0 4 2 5 6 3 0 7 1 1 60

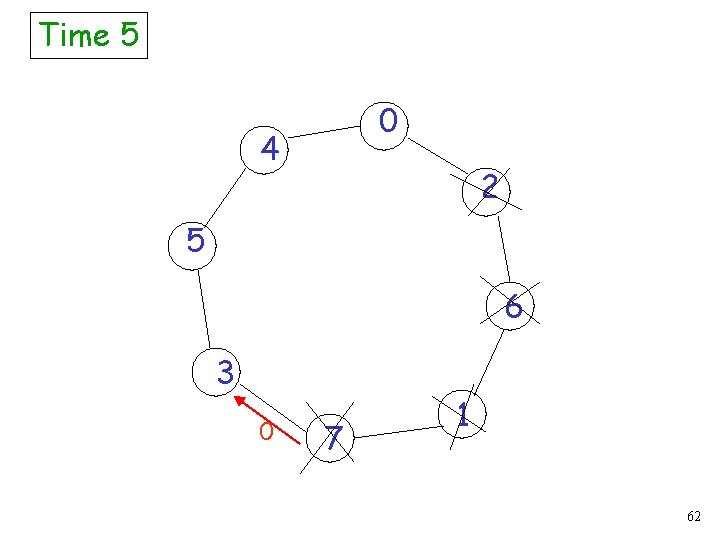
Time 4 0 4 2 5 6 3 1 7 1 0 61

Time 5 0 4 2 5 6 3 0 7 1 62

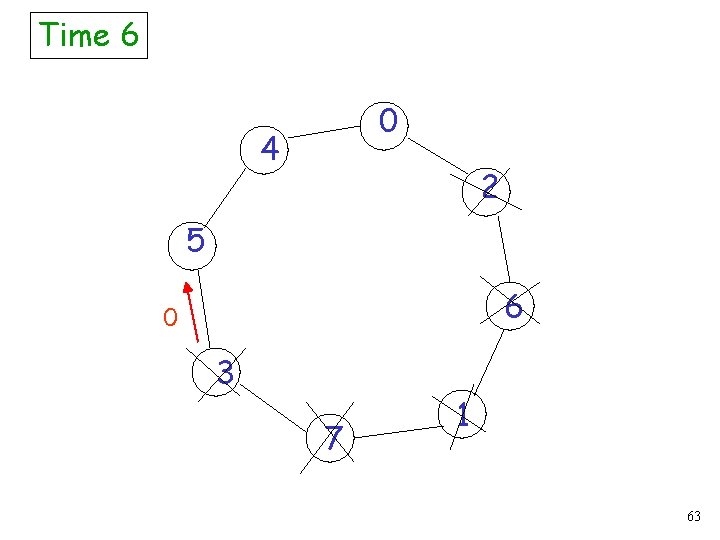
Time 6 0 4 2 5 6 0 3 7 1 63

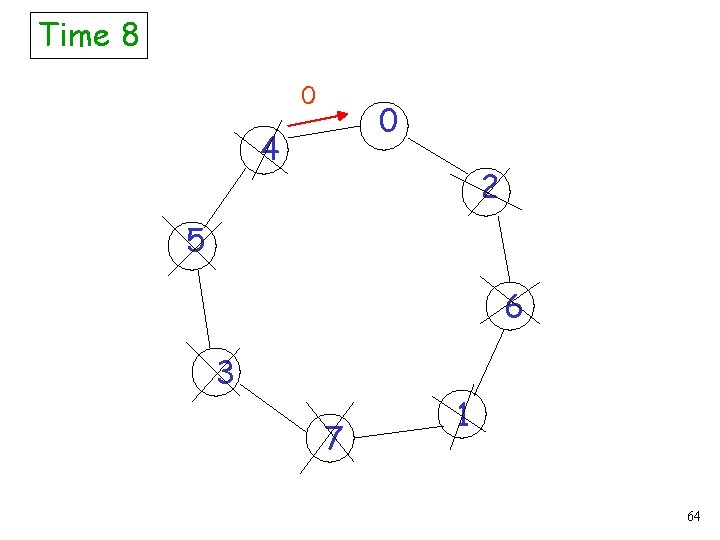
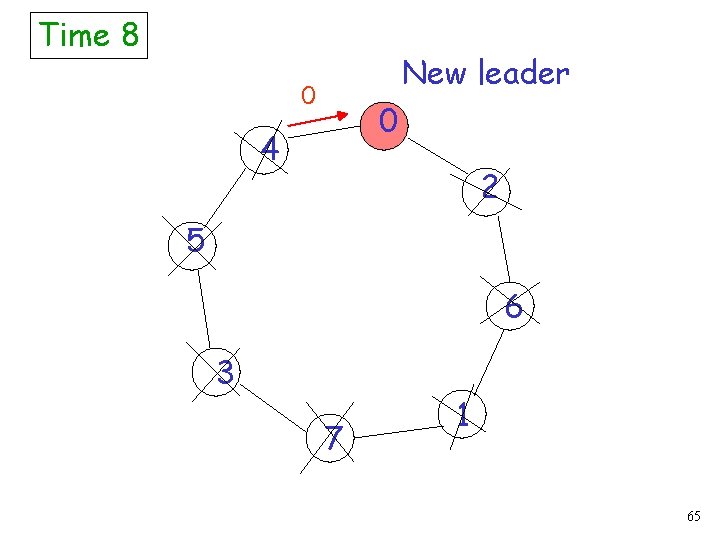
Time 8 0 0 4 2 5 6 3 7 1 64

Time 8 New leader 0 0 4 2 5 6 3 7 1 65

Message complexity Assume leader has (smallest) id Total time of algorithm: Note that if is exponentially slow then algorithm 66

Take the node with immediately higher id Total number of messages: 67

Take the node with immediately higher id Total number of messages: 68

lower id messages higher Total messages: 69

An Lower Bound Assume we have algorithms in which: • the network is asynchronous • the maximum identifier is elected leader • all the nodes must know the leader • the size of the network We will prove: at least to elect a leader is not known messages are needed 70

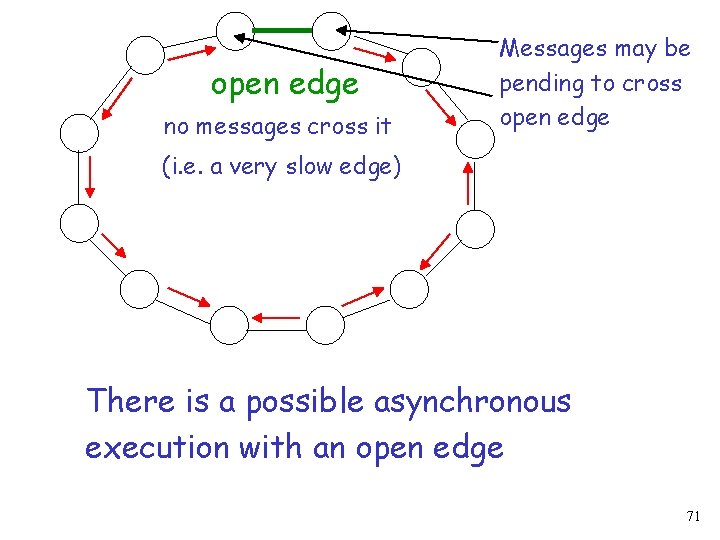
open edge no messages cross it Messages may be pending to cross open edge (i. e. a very slow edge) There is a possible asynchronous execution with an open edge 71

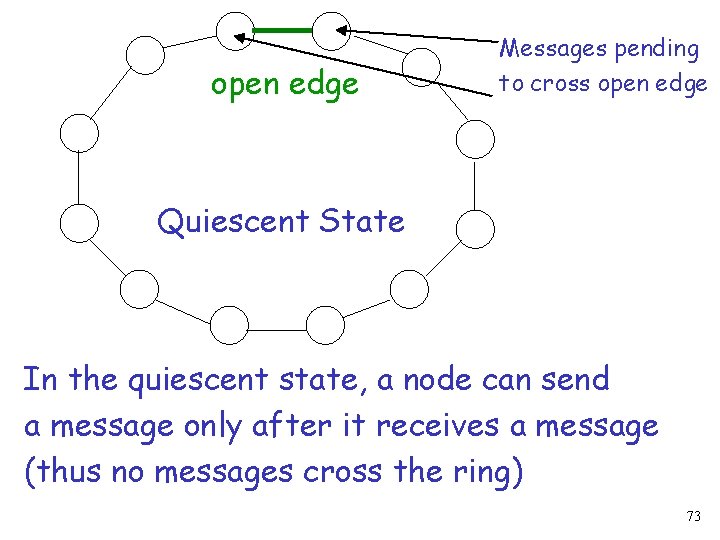
open edge Messages pending to cross open edge Quiescent State If the edge remains open, then the execution will eventually reach a quiescent state where not more messages cross the ring 72

open edge Messages pending to cross open edge Quiescent State In the quiescent state, a node can send a message only after it receives a message (thus no messages cross the ring) 73

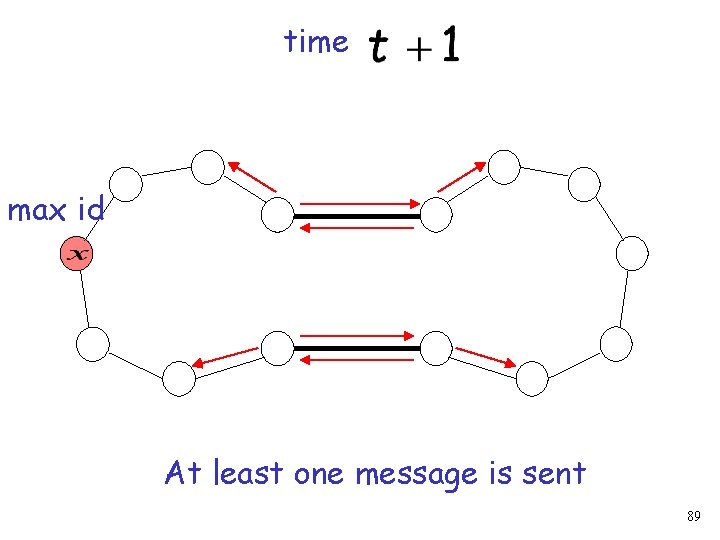
Time t Suppose that the edge closes This may cause a propagation of messages until the algorithm terminates 74

Time t+1 This may cause a propagation of messages until the algorithm terminates 75

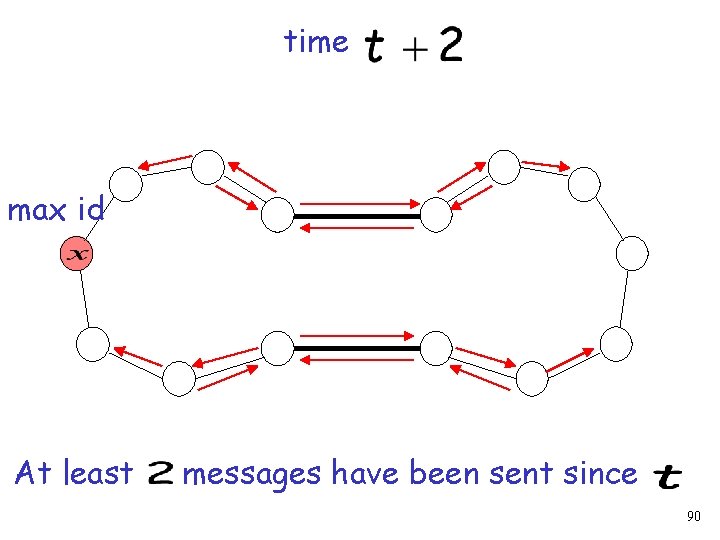
Time t+2 This may cause a propagation of messages until the algorithm terminates 76

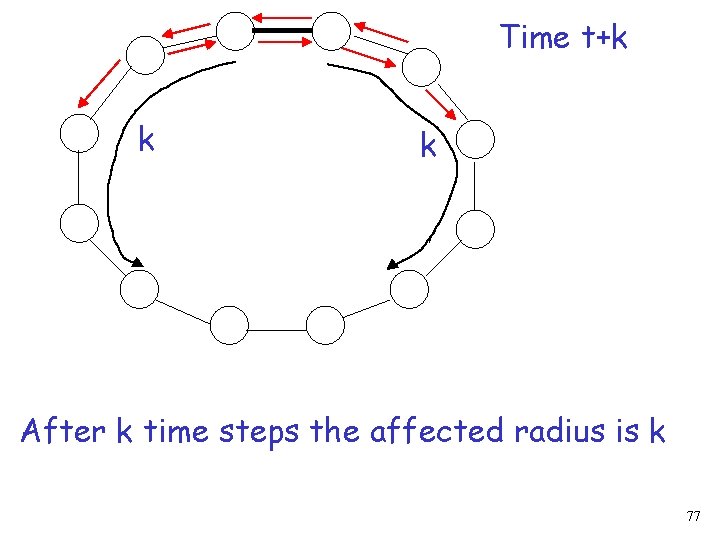
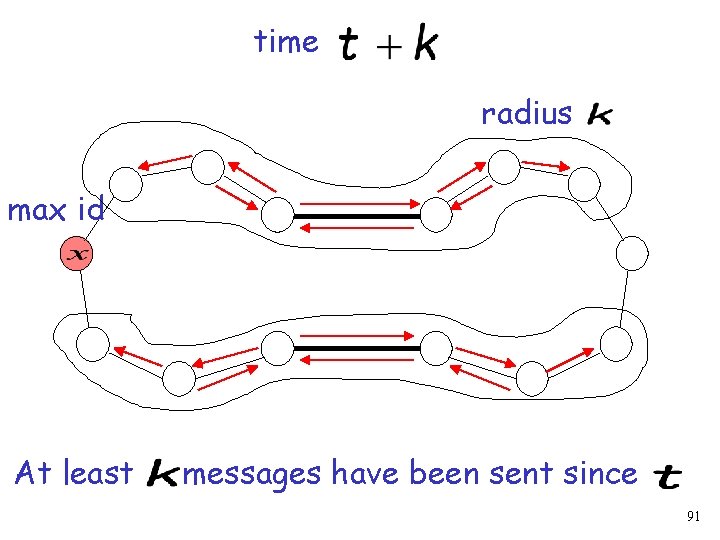
Time t+k k k After k time steps the affected radius is k 77

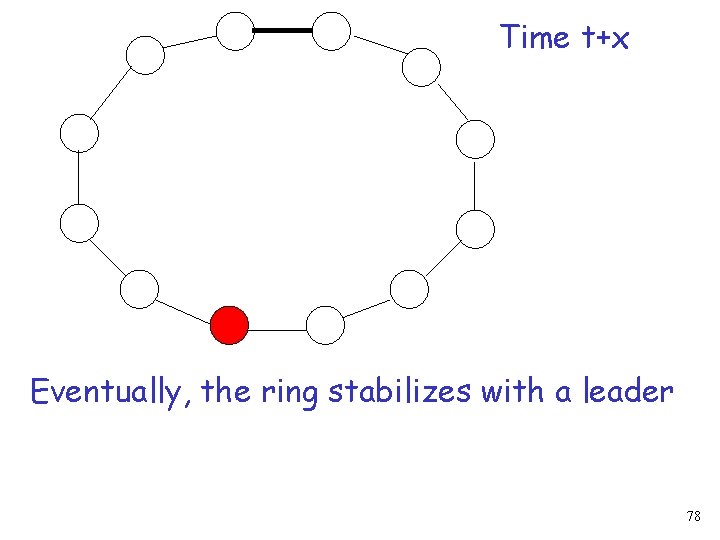
Time t+x Eventually, the ring stabilizes with a leader 78

We will show, that there is an execution with nodes such that: • there is an open edge • at least messages are received where 79

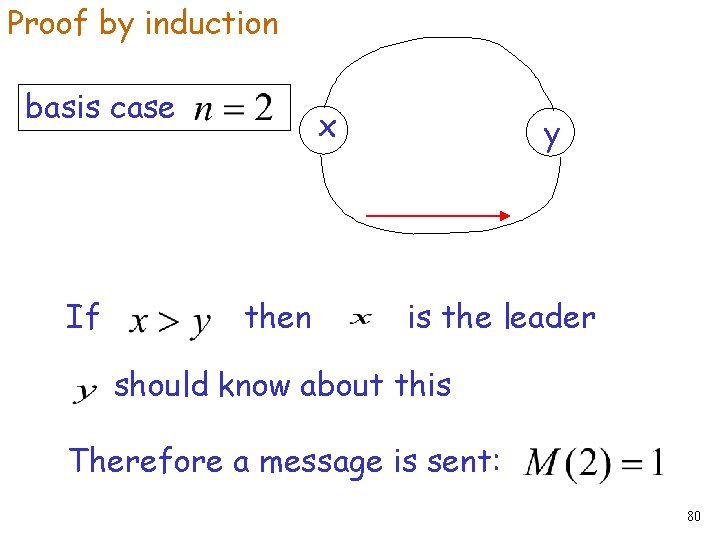
Proof by induction basis case If x then y is the leader should know about this Therefore a message is sent: 80

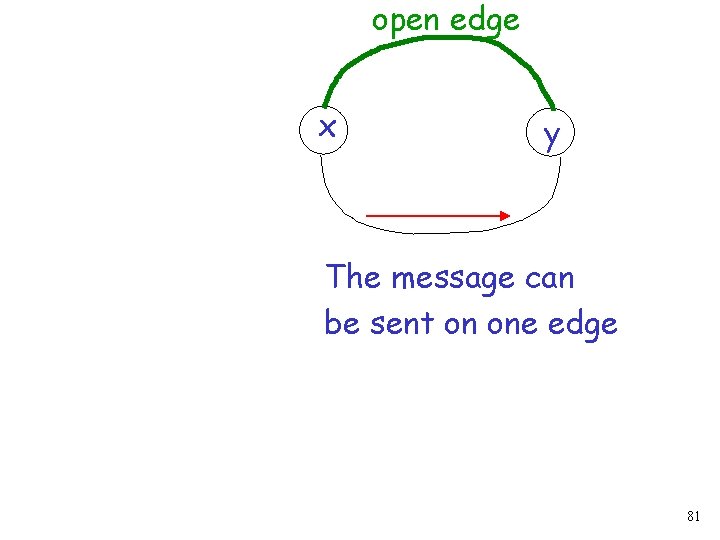
open edge x y The message can be sent on one edge 81

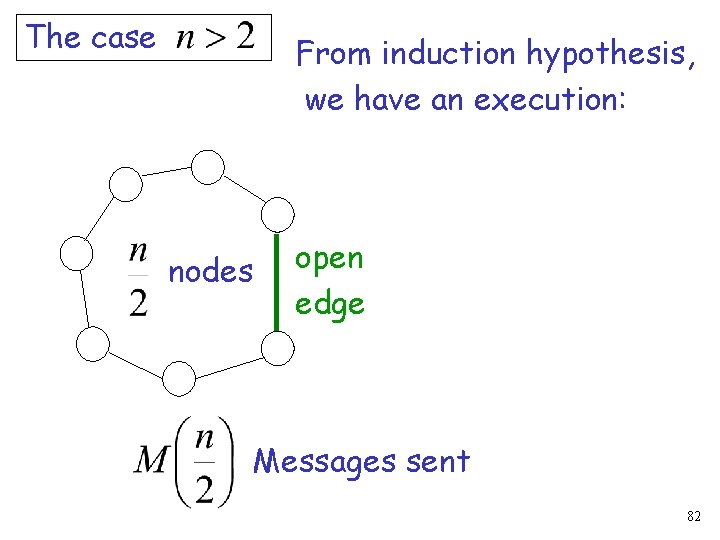
The case From induction hypothesis, we have an execution: nodes open edge Messages sent 82

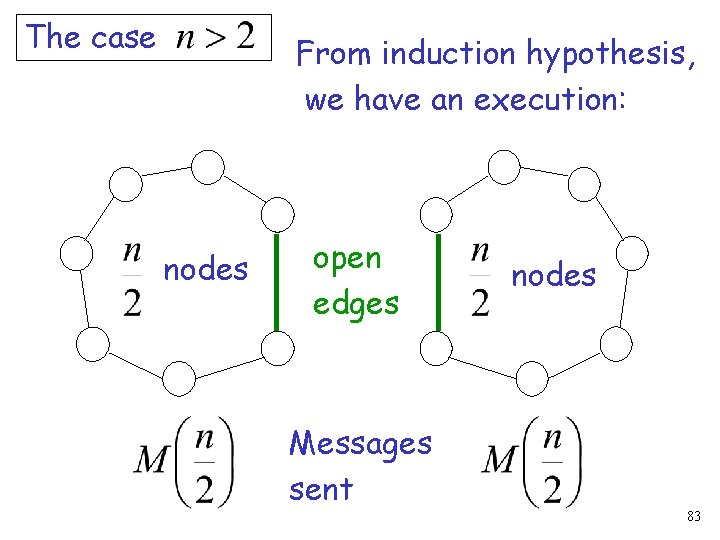
The case From induction hypothesis, we have an execution: nodes open edges Messages sent nodes 83

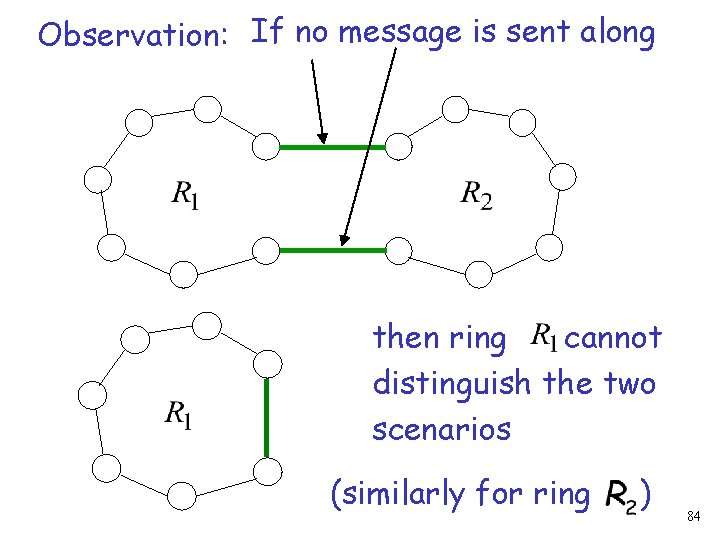
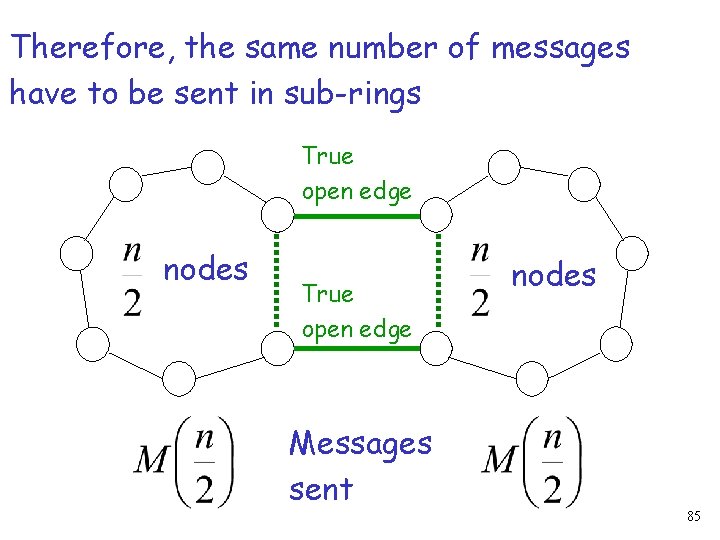
Observation: If no message is sent along then ring cannot distinguish the two scenarios (similarly for ring ) 84

Therefore, the same number of messages have to be sent in sub-rings True open edge nodes True open edge Messages sent nodes 85

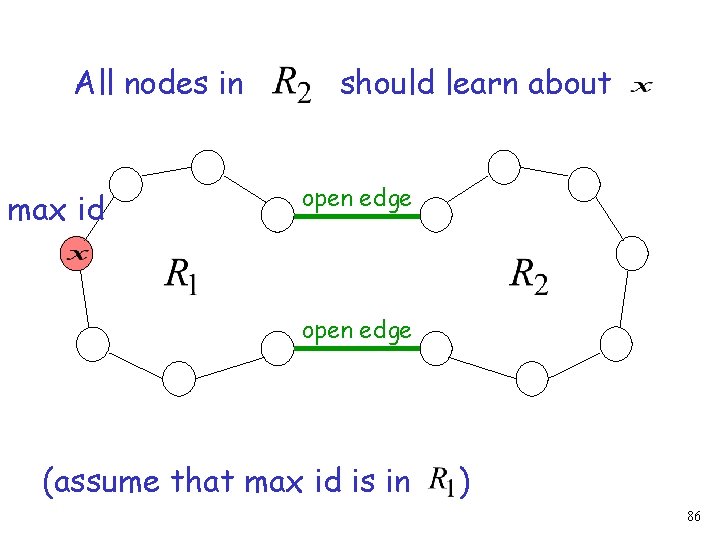
All nodes in max id should learn about open edge (assume that max id is in ) 86

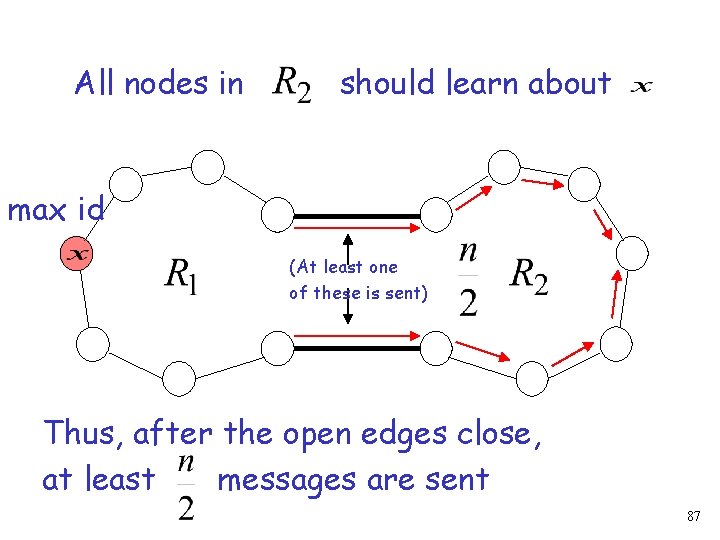
All nodes in should learn about max id (At least one of these is sent) Thus, after the open edges close, messages are sent at least 87

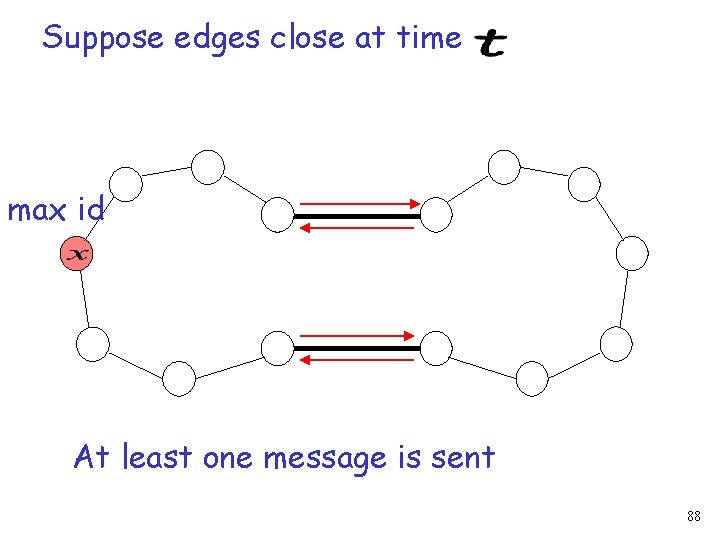
Suppose edges close at time max id At least one message is sent 88

time max id At least one message is sent 89

time max id At least messages have been sent since 90

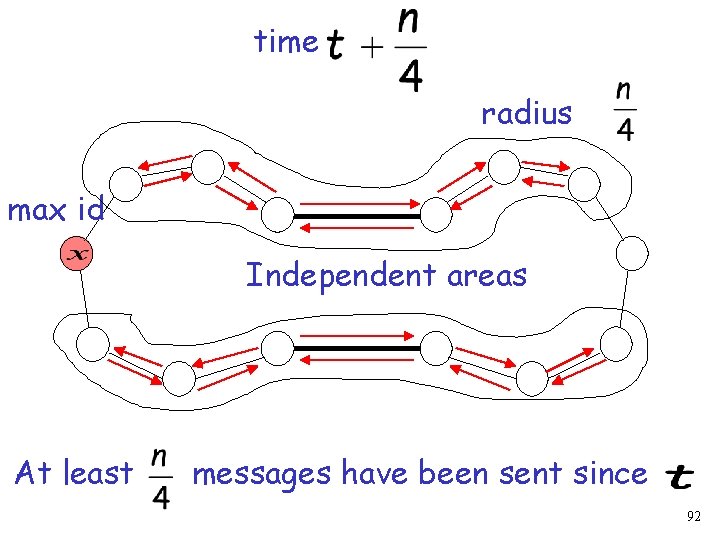
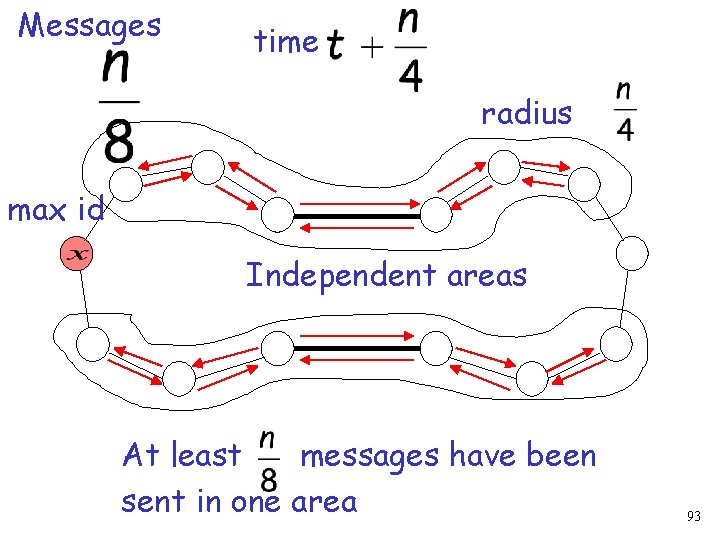
time radius max id At least messages have been sent since 91

time radius max id Independent areas At least messages have been sent since 92

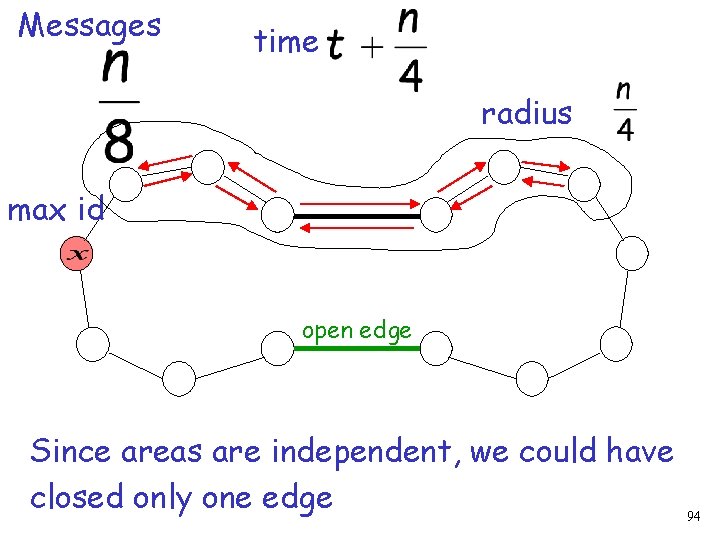
Messages time radius max id Independent areas At least messages have been sent in one area 93

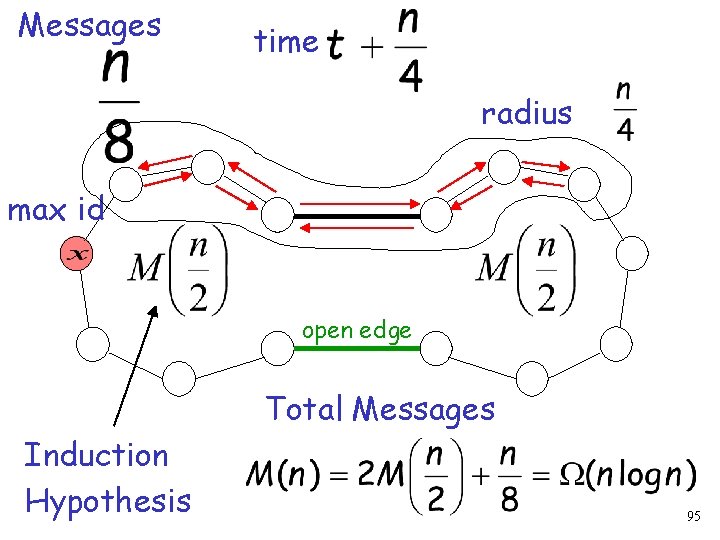
Messages time radius max id open edge Since areas are independent, we could have closed only one edge 94

Messages time radius max id open edge Total Messages Induction Hypothesis 95