III Les tests statistiques au service de la

III Les tests statistiques au service de la modélisation

Modélisation Les statistiques sont souvent employées pour analyser des résultats d'expériences réalisées dans le but de tester un modèle.

Un modèle permet de faire des prédictions Ce modèle va permettre de pouvoir faire des prédictions : dans le cas de variables qualitatives, sur les fréquences Exemple : dé non pipé : n/6 occurrences pour chaque valeur Dans le cas de variable quantitatives, décrivent le comportement de la variable aléatoire sur la population Exemple : le taux de progestérone mesurée sur un troupeau de brebis dépend son alimentation en protéine � =� +C×param+� 0

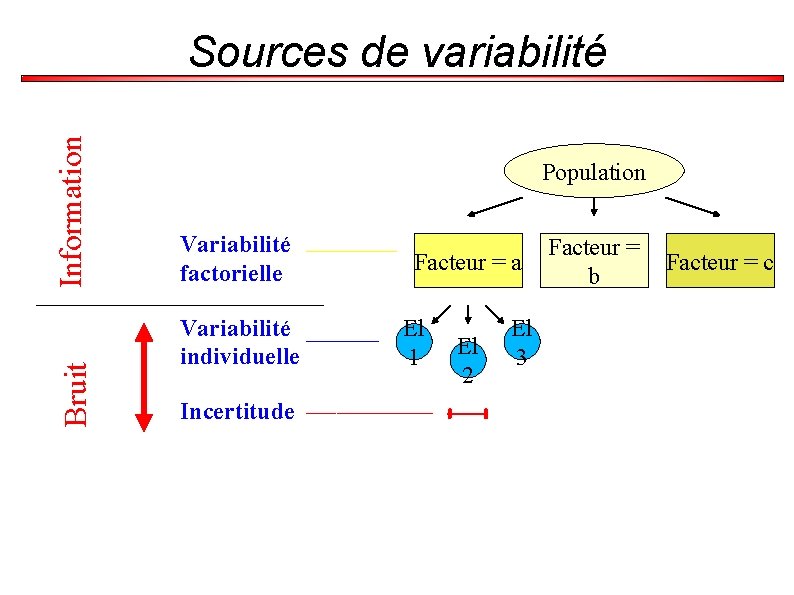
Problème expérimental Même si le modèle s'avérait exact, nous ne retrouverions pas exactement ses prédictions à cause de la variabilité de la mesure d'un paramètre dans une population Il y a plusieurs sources de variabilités : l'imprécision de la mesure la variabilité individuelle la variabilité factorielle

Sources de variabilité (1) Imprécision de la mesure On effectue une mesure sur un élément. On la répète dans les mêmes conditions. La mesure est différente. Nous avons là un exemple d'imprécision de la mesure.

Sources de variabilité Imprécision ≠ Inexactitude Si la mesure effective diffère de la valeur réelle, on parle alors d'inexactitude. Elle souvent due à une erreur dans le protocole expérimental. Elle est aussi introduite lorsqu'on étudie un échantillon peu représentatif de la population. Attention : l'inexactitude peut être masquée

Sources de variabilité (2) Différences individuelles Les éléments de l'échantillon sont différents.

Sources de variabilité (3) Différences factorielles Les éléments placés dans un environnement différent ont des propriétés différentes. On cherche souvent à caractériser de telles différences.

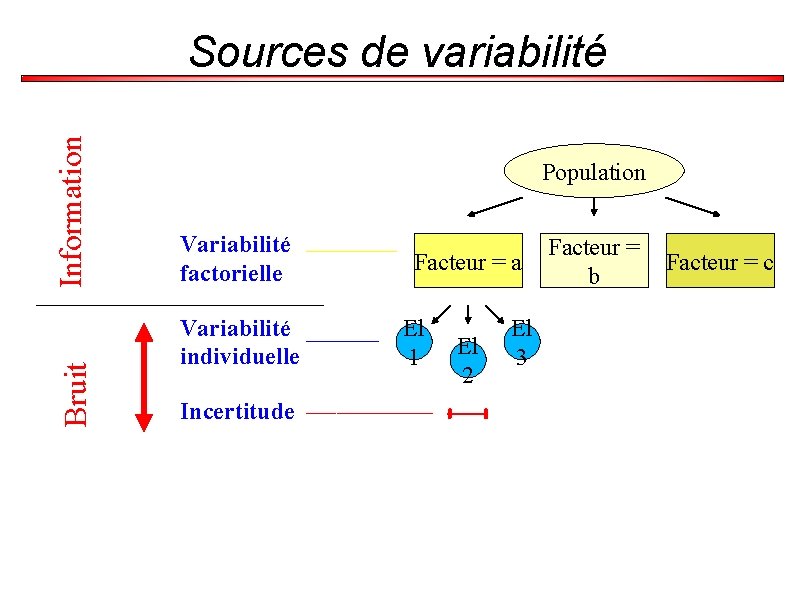
Sources de variabilité Variabilité résiduelle = imprécision + variabilité individuelle Variabilité totale = variabilité résiduelle + variabilité factorielle

Bruit Information Sources de variabilité Population Variabilité factorielle Variabilité individuelle Incertitude Facteur = a El 1 El 2 El 3 Facteur = b Facteur = c

Repérer les sources de variabilité (1) Imprécision : faire la mesure 2 fois, dans les mêmes conditions, sur le même élément. (2) Variabilité individuelle : faire la mesure dans les mêmes conditions, sur au moins 2 éléments. (3) Variabilité factorielle : faire la mesure dans les mêmes conditions, sur au moins 2 éléments sur 2 niveaux de ce facteur.

Réduire les sources de variabilité (1) Imprécision : Améliorer la technique de mesure (2) Variabilité individuelle : Standardiser l'expérience en ne mélangeant pas différentes groupes dans l'étude. Bien définir la population (3) Variabilité factorielle : Irréductible. La variabilité factorielle est souvent ce que l'on veut mettre en évidence.

Tester un modèle Les résultats expérimentaux apportent des informations sur la validité du modèle. Ces sources de variabilités vont entraîner une incertitude dans l'interprétation des résultats. Le but de l'expérience est de décider de la validité du modèle Nous allons donc employer la théorie des tests statistiques

III-1) Comparaison de fréquences expérimentales et de fréquences théoriques

Comparaisons de fréquences Certains modèles théoriques prédisent la répartition du nombre de résultats (=fréquences)pour chaque valeur possible du résultat Exemples Cas du dé non pipé Les fréquences de chaque chiffre sont égales Découverte des lois de la génétique par Mendel. ¾ des individus de 2ème génération présentent le caractère dominant.

Résultats expérimentaux Les résultats expérimentaux ne correspondent pas exactement aux résultats théoriques. Exemples Cas du dé non pipé Même si le dé n'est pas pipé, je trouve les résultats : {1: 5, 2: 4, 3: 6 , 4: 5, 5: 6, 6: 4} sur 30 lancers Le résultat idéal {1: 5, 2: 5, 3: 5 , 4: 5, 5: 5, 6: 5} n'avait qu'une probabilité de 8% d'être obtenue. Découverte des lois de la génétique par Mendel. Les résultats de Mendel ne donnaient pas parfaitement un rapport de ¾ !

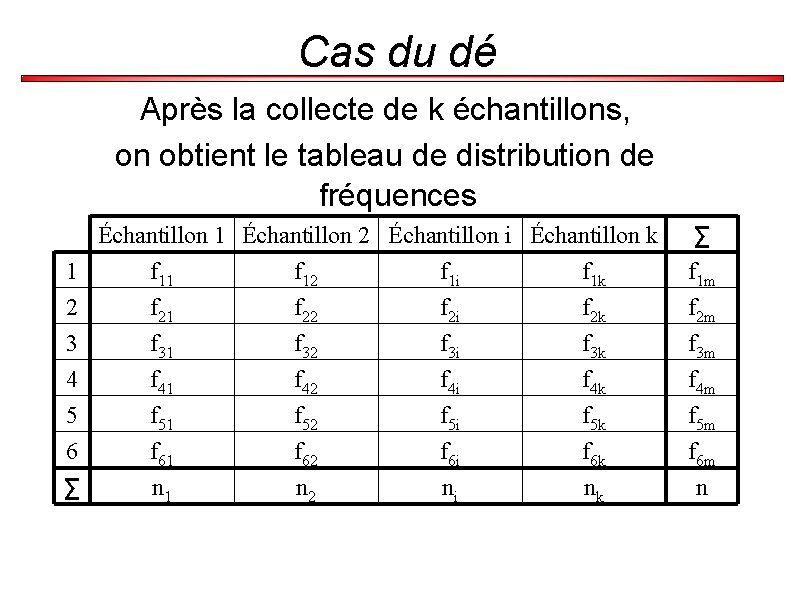
Cas du dé Après la collecte de k échantillons, on obtient le tableau de distribution de fréquences 1 2 3 4 5 6 ∑ Échantillon 1 Échantillon 2 Échantillon i Échantillon k f 11 f 12 f 1 i f 1 k f 21 f 22 f 2 i f 2 k f 31 f 32 f 3 i f 3 k f 41 f 42 f 4 i f 4 k f 51 f 52 f 5 i f 5 k f 61 f 62 f 6 i f 6 k n 1 n 2 ni nk ∑ f 1 m f 2 m f 3 m f 4 m f 5 m f 6 m n

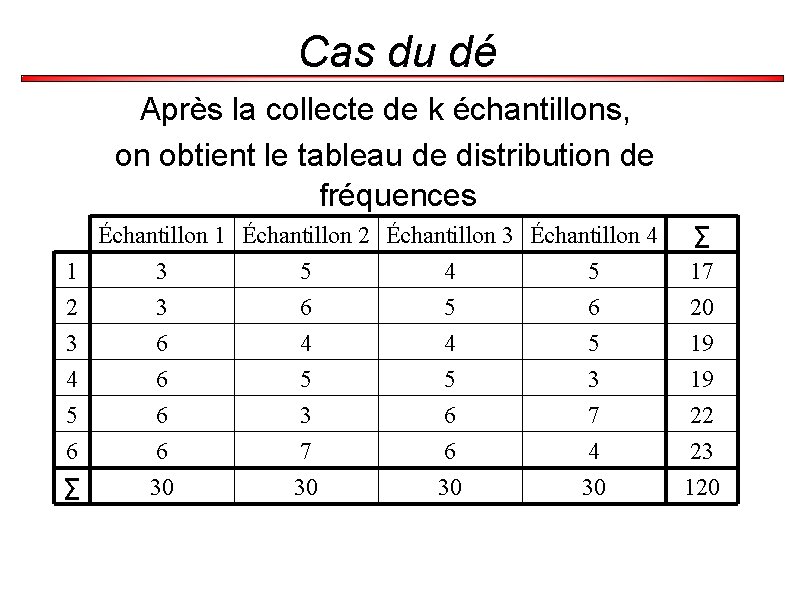
Cas du dé Après la collecte de k échantillons, on obtient le tableau de distribution de fréquences 1 2 3 4 5 6 ∑ Échantillon 1 Échantillon 2 Échantillon 3 Échantillon 4 3 5 4 5 3 6 5 6 6 4 4 5 6 5 5 3 6 7 6 4 30 30 ∑ 17 20 19 19 22 23 120

Comparaison des fréquences à une théorie (1) Formuler ses hypothèses On veut savoir si les fréquences expérimentales reproduisent bien les fréquences théoriques H 0 : Pour tout i, E(fexp, i)=fth, i L'espérance E(fexp, i) est la moyenne de la distribution de probabilité de fexp, i. Nous allons prendre pour l'instant H 1 : Il y a un i tel que E(fexp, i)≠fth, i Cette définition H 1 de ne nous donne pas de critère commode, à appliquer sans distinguer de cas.

Mesurer l'écart de la mesure à la théorie Les fréquences observées diffèrent des fréquences théoriques. Pour quantifier la distance entre les deux fréquences, on peut utiliser la distance : Cette distance augmente arbitrairement avec la taille de l'échantillon. – Pour 30 lancers de dé : la fréquence attendue est de 5 pour tous les chiffres. on obtient {1: 5, 2: 4, 3: 6 , 4: 5, 5: 6, 6: 4}. La distance est alors de 4. – Pour 300 lancers de dé : la fréquence attendue est de 50 pour tous les

Mesurer l'écart de la mesure à la théorie L'idée est alors de renormaliser cette quantité par les fréquences attendues. La nouvelle quantité est indépendante de la taille de l'échantillon choisie. Cette distance augmente arbitrairement avec la taille de l'échantillon. – Pour 30 lancers de dé : la fréquence attendue est de 5 pour tous les chiffres. on obtient {1: 5, 2: 4, 3: 6 , 4: 5, 5: 6, 6: 4}. La distance est alors de 4/5.

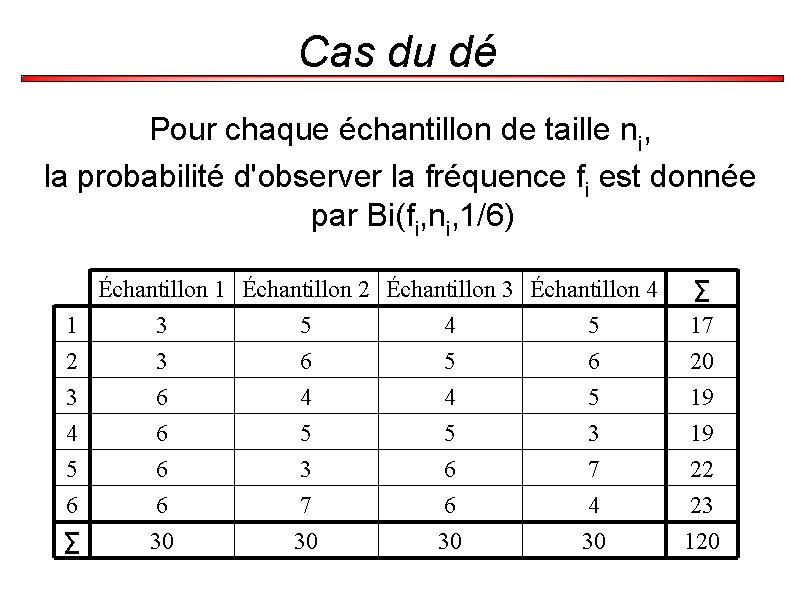
Cas du dé Pour chaque échantillon de taille ni, la probabilité d'observer la fréquence fi est donnée par Bi(fi, ni, 1/6) 1 2 3 4 5 6 ∑ Échantillon 1 Échantillon 2 Échantillon 3 Échantillon 4 3 5 4 5 3 6 5 6 6 4 4 5 6 5 5 3 6 7 6 30 7 30 6 30 4 30 ∑ 17 20 19 19 22 23 120

Cas du dé Si la taille de l'échantillon, ni, devient très grande, cette probabilité, Bi(fi, ni, 1/6), se rapproche d'une loi normale de moyenne ni/6 et de variance /1/6× 5/6×√ni. C'est une conséquence du théorème central limite.

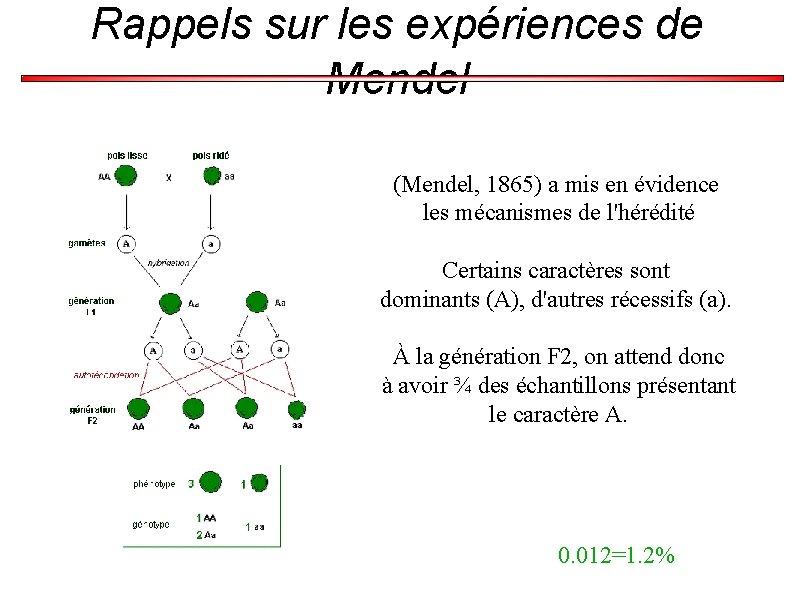
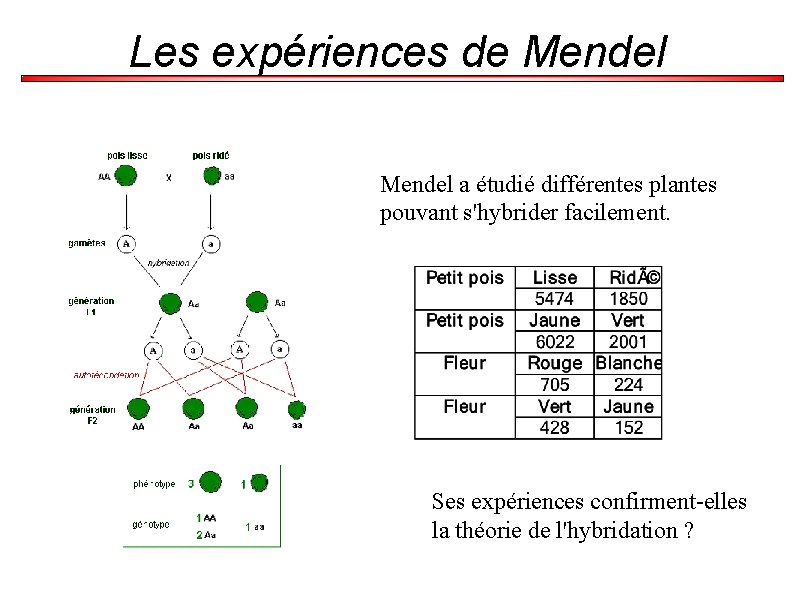
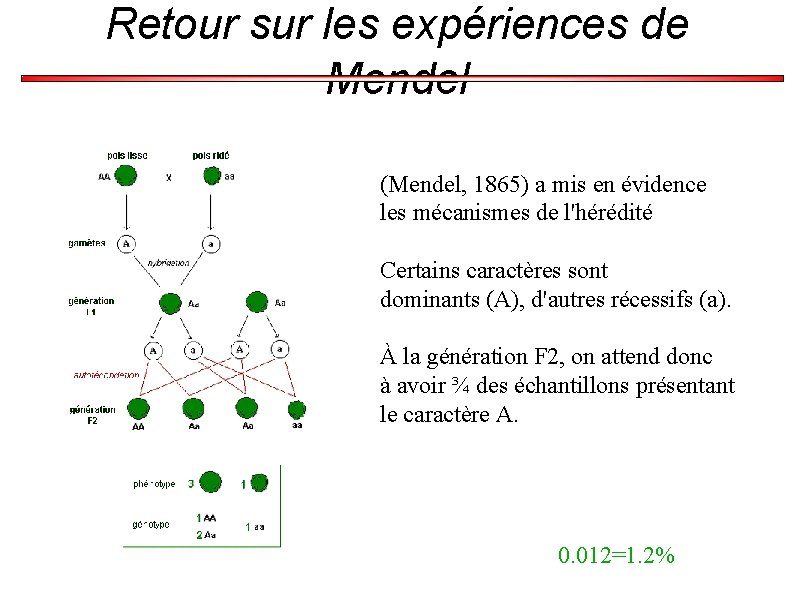
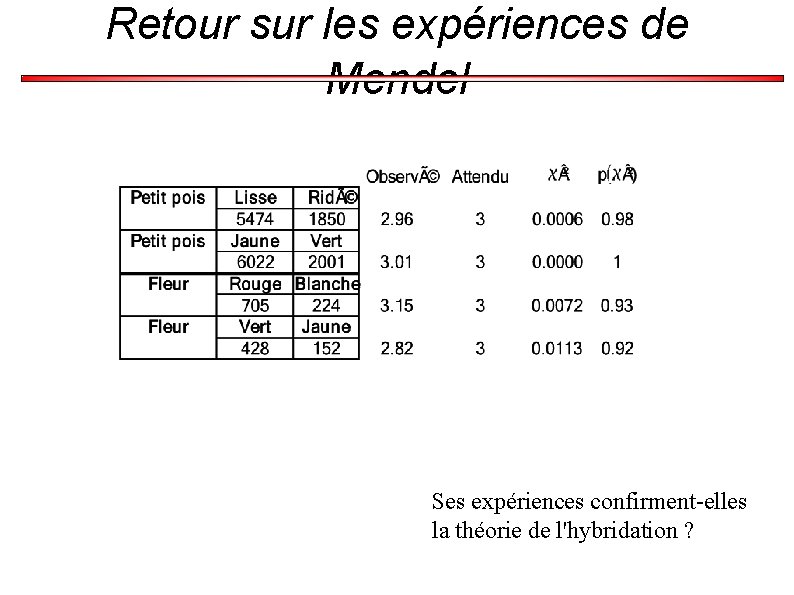
Rappels sur les expériences de Mendel (Mendel, 1865) a mis en évidence les mécanismes de l'hérédité Certains caractères sont dominants (A), d'autres récessifs (a). À la génération F 2, on attend donc à avoir ¾ des échantillons présentant le caractère A. 0. 012=1. 2%

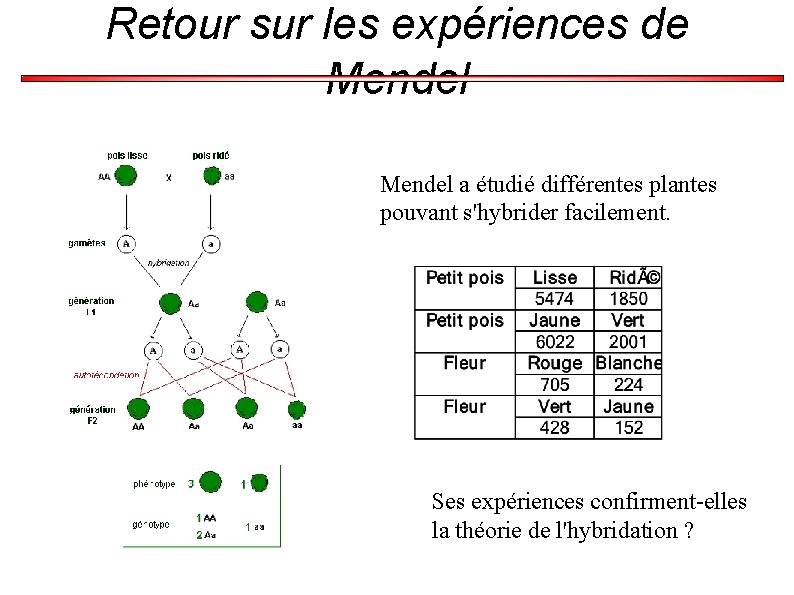
Les expériences de Mendel a étudié différentes plantes pouvant s'hybrider facilement. Ses expériences confirment-elles la théorie de l'hybridation ?

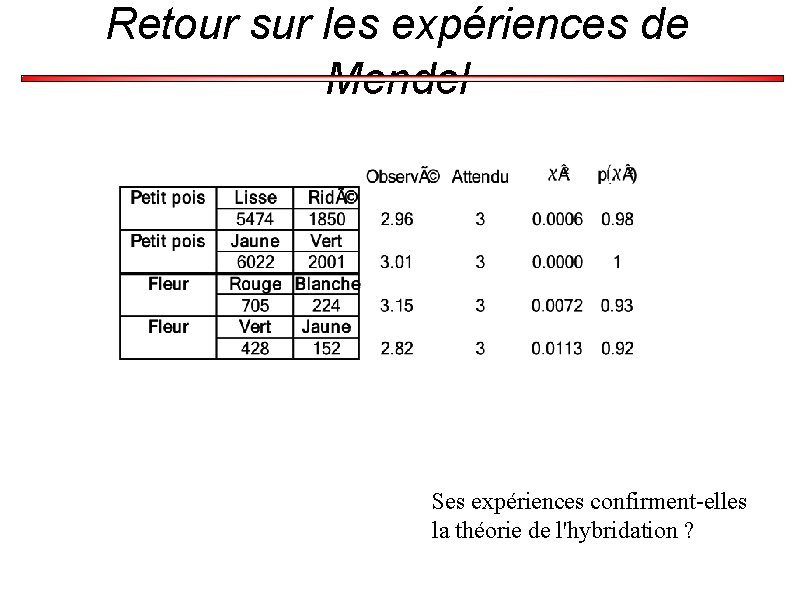
Retour sur les expériences de Mendel Ses expériences confirment-elles la théorie de l'hybridation ?

III-2) Test d'un modèle liant deux paramètres - ANOVA -

Modélisation On identifie la variabilité factorielle sous-groupe i individu i, j de ce sous groupe X=� +a + e

ANOVA Le terme vient de l'anglais « ANalysis Of VAriances » Il faut plutôt le comprendre comme Comparaison de variabilités

Sources de variabilité La variabilité totale résulte de : la variabilité factorielle Si on classe les données en fonction d'un facteur, c'est la variabilité entre les groupes (variabilité intergroupe) la variabilité résiduelle Si on classe les données en fonction d'un facteur, c'est la variabilité dans chaque groupe (variabilité intragroupe)

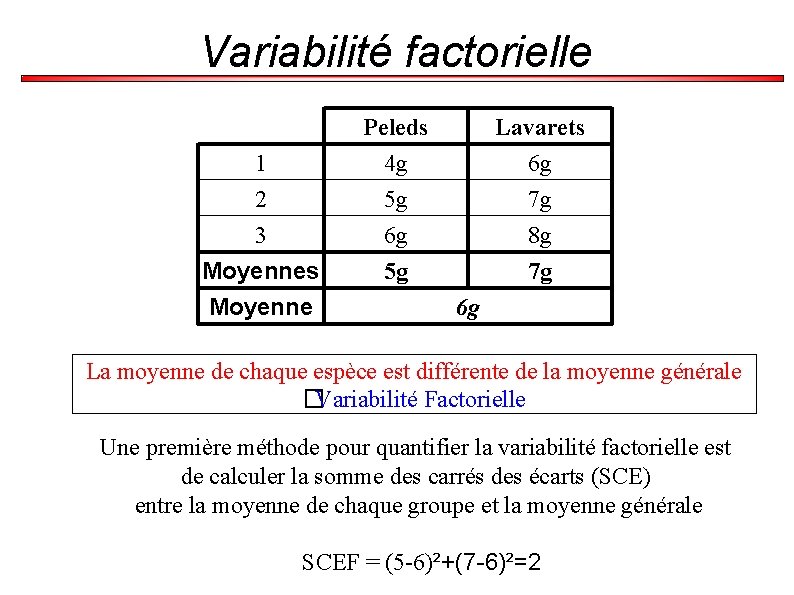
Sources de variabilité On pèche dans un lac 6 poissons de deux espèces différentes. On mesure pour chaque poisson poids : 1 2 3 Moyennes Moyenne Peleds 4 g 5 g 6 g 5 g Lavarets 6 g 7 g 8 g 7 g 6 g La moyenne de chaque espèce est différente de la moyenne générale �Variabilité factorielle – Variabilité intergroupe Un poisson n'a pas forcément le poids moyen de son espèce �Variabilité résiduelle – Variabilité intragroupe

Quantification des variabilités On a besoin de quantifier ces deux types de variabilités : la variabilité intragroupe On somme les écarts entre chaque valeur du sousgroupe et la moyenne du sous-groupe la variabilité intergroupe On somme les écarts entre la moyenne de chaque sous-groupe et la moyenne générale. On pondère par le nombre d'éléments de chaque groupe.

Variabilité résiduelle 1 2 3 Moyennes Moyenne Peleds 4 g 5 g 6 g 5 g Lavarets 6 g 7 g 8 g 7 g 6 g Un poisson n'a pas forcément le poids moyen de son espèce �Variabilité Résiduelle La variabilité résiduelle est quantifiée en calculant la somme des carrés des écarts (SCE) entre les valeurs de chaque groupe et la moyenne de chaque groupe SCERpeleds = (4 -5)²+(5 -5)²+(6 -5)²=2 SCERlavarets = (6 -7)²+(7 -7)²+(8 -7)²=2

Variabilité résiduelle 1 2 3 Moyennes Moyenne Peleds 4 g 5 g 6 g 5 g Lavarets 6 g 7 g 8 g 7 g 6 g �Variabilité Résiduelle Afin d'éviter de manipuler plusieurs SCER, on se contente d'une mesure de variabilité résiduelle totale SCER = ∑SCERgroupes Ici, SCER=SCERpeleds+SCERlavarets=2+2=4

Variabilité factorielle 1 2 3 Moyennes Moyenne Peleds 4 g 5 g 6 g 5 g Lavarets 6 g 7 g 8 g 7 g 6 g La moyenne de chaque espèce est différente de la moyenne générale �Variabilité Factorielle Une première méthode pour quantifier la variabilité factorielle est de calculer la somme des carrés des écarts (SCE) entre la moyenne de chaque groupe et la moyenne générale SCEF = (5 -6)²+(7 -6)²=2

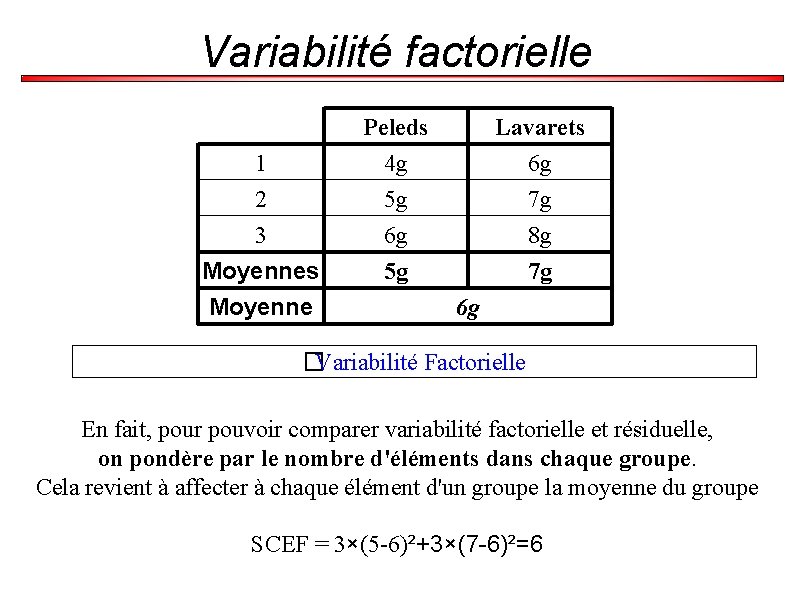
Variabilité factorielle 1 2 3 Moyennes Moyenne Peleds 4 g 5 g 6 g 5 g Lavarets 6 g 7 g 8 g 7 g 6 g �Variabilité Factorielle En fait, pour pouvoir comparer variabilité factorielle et résiduelle, on pondère par le nombre d'éléments dans chaque groupe. Cela revient à affecter à chaque élément d'un groupe la moyenne du groupe SCEF = 3×(5 -6)²+3×(7 -6)²=6

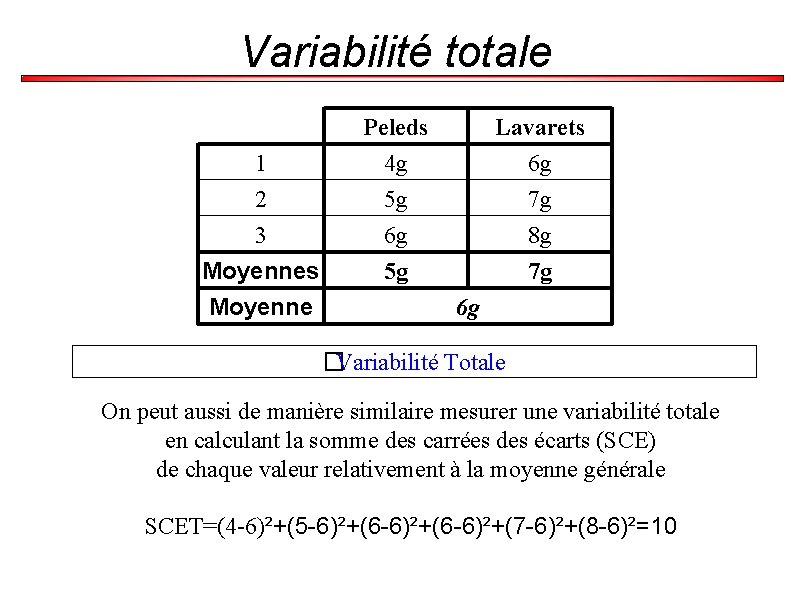
Variabilité totale 1 2 3 Moyennes Moyenne Peleds 4 g 5 g 6 g 5 g Lavarets 6 g 7 g 8 g 7 g 6 g �Variabilité Totale On peut aussi de manière similaire mesurer une variabilité totale en calculant la somme des carrées des écarts (SCE) de chaque valeur relativement à la moyenne générale SCET=(4 -6)²+(5 -6)²+(6 -6)²+(7 -6)²+(8 -6)²=10

Relation entre variabilités �Variabilité Factorielle SCEF=6 �Variabilité Résiduelle SCER=4 �Variabilité Totale SCET=10 On remarque qu'on obtient la relation SCET = SCEF + SCER variabilité totale = variabilité factorielle + variabilité résiduelle

Relation entre variabilités SCET = SCEF + SCER variabilité totale = variabilité factorielle + variabilité résiduelle On peut démontrer que cette relation est en fait générale

Relation entre variabilités

Notations Effectif de chaque groupe : nk Effectif total : N Moyenne générale <X> Moyenne de chaque groupe <X>k Nombre de groupes K Ces notations permettent de simplifier l'écriture des SCE

Notations Effectif de chaque groupe : nk Effectif total : N Moyenne générale <X> Moyenne de chaque groupe <X>k Nombre de groupes K Nous avons aussi les relations

Simplification du calcul des variabilités En remarquant que ∑(Xi-<X>)²=∑Xi²-∑<X>² (comme lors du calcul de la variance en statistiques descriptives) et en factorisant les termes constants (comme <X>), on peut mettre les SCE sous une forme plus adaptée au calcul

ANOVA et test d'égalité de moyenne On remarque si on suppose que les moyennes de sous-populations sont égales, on a tendance à avoir SCEF=0 c'est à dire qu'en cas d'égalité des moyennes SCET=SCER On s'est ramené à un problème d'égalité de variances !

Hypothèse d'égalité des variances On suppose que la variance associée à la variabilité résiduelle est la même pour la population traitée et la population originale

Comparaison d'une moyenne à une référence Pour tester le médicament, on mesure la pression artérielle sur un échantillon traitée et on compare la moyenne de la population saine. On suppose H 0. Comme on connaît la probabilité d'obtention des résultats dans ce cas, on peut déterminer une valeur seuil. Si les résultats expérimentaux ne sont pas compatibles avec la valeur seuil, l'hypothèse H 0 est rejetée. Sinon elle est acceptée.

Comparaison d'une moyenne à une référence Puisque H 1 est asymétrique (� <0) le seuil est calculé par P

Hypothèse d'égalité des variances On suppose que la variance associée à la variabilité résiduelle est la même pour la population traitée et la population originale

Comparaison d'une moyenne à une référence Pour tester le médicament, on mesure la pression artérielle sur un échantillon traitée et on compare la moyenne de la population saine. On suppose H 0. Comme on connaît la probabilité d'obtention des résultats dans ce cas, on peut déterminer une valeur seuil. Si les résultats expérimentaux ne sont pas compatibles avec la valeur seuil, l'hypothèse H 0 est rejetée. Sinon elle est acceptée.

Comparaison d'une moyenne à une référence Puisque H 1 est asymétrique (� <0) le seuil est calculé par P

Étapes d'un test d'hypothèse (1) Formuler ses hypothèses Poser H 0 et H 1 (2) Choix du test approprié Le cours est là pour vous présenter les tests (3) Spécifier un niveau de signification (� ) et la taille de l'échantillon (N) (4) Trouver la distribution d'échantillonnage du test statistique (5) Calculer la région de rejet (6) Tirer une conclusion Si la probabilité est très faible, on rejette l'hypothèse

Hypothèse statistique ● Puissance statistique : (1 - – – – c’est l’aptitude à mettre en évidence une différence lorsqu’elle existe cf Test diagnostic : sensibilité on calcule un nombre de sujets nécessaire pour obtenir une puissance donnée

Hypothèse statistique 6. Le degré de signification ( « p » ) Ex : si les taux de succès sous corticoïdes et sous placebo sont identiques, la probabilité d’observer une telle différence (i. e. 51, 2% vs 23, 8%) ou une différence plus grande encore est de 0, 009

Hypothèse statistique ● Définition : – – quantifie le « désaccord » entre ce qu’on observe et l’hypothèse nulle H 0 la probabilité d’observer des résultats au moins aussi en désaccord avec l’hypothèse nulle H 0 que ceux qu’on a observés

Comparaisons de fréquences Nous effectuons des expériences pour confirmer des résultats théoriques, qui prédisent une répartition de nos résultats. Pour effectuer cette comparaison, nous comparons

Hypothèse statistique ● Interprétation : – plus le degré de signification est faible, plus on est convaincu que les résultats observés ne sont pas en cohérence avec l’hypothèse nulle

Hypothèse statistique ATTENTION !!!! (1) Le degré de signification nous permet d’affirmer avec plus ou moins de conviction qu’il y a une différence, mais en aucun cas il ne nous renseigne sur l’importance de cette différence

Hypothèse statistique ● Exemple : – – – 1) 22/43 (51, 2%) vs 10/42 (23, 8%) Différence d’efficacité = 27, 4% (p = 0, 009) 2) 14/22 (63, 6%) vs 5/21 (23, 8%) Différence d’efficacité = 39, 8% (p = 0, 009) 3) 1104/4200 (26, 3%) vs 1000/4200 (23, 8%) Différence d’efficacité = 2, 5% (p = 0, 009)

Test d'hypothèse = détermination de la plausibilité qu'un paramètre d'un modèle prenne des valeurs différentes dans des populations distinctes, afin de mettre en évidence, ou non, un effet d'un facteur expérimental sur une population.

Hypothèse statistique ● La valeur de p dépend : – – ● de la différence observée entre les deux groupes de la taille d’échantillon S’il existe une différence réelle, aussi infime soit-elle, entre 2 groupes, n’importe quel test statistique va aboutir à une valeur de p inférieure à 0, 05, dès lors que le nombre de sujets étudiés sera important

Hypothèse statistique La signification statistique n’implique pas la pertinence clinique

Courbe de puissance d'un test statistique Souvent on ne connaît pas la loi de probabilité de H 1 car il nous manque un seul paramètre. Dans le cas du dé, ce serait de connaître la probabilité de tirer un 1 Courbe de puissance (d'un test statistique) = Courbe caractéristique d'efficacité = Fonction donnant 1 -� pour chaque valeur du paramètre inconnu de H 1, pour �donné.

Hypothèse statistique ATTENTION !!!! (2) Ne pas mettre en évidence de différence statistiquement significative entre deux groupes ne signifie pas qu’il y ait équivalence entre les deux groupes

Hypothèse statistique ● Ex : 0/3 (0, 0%) vs 3/3 (100, 0%) Différence d’efficacité = 100, 0% p = 0, 010 (test exact de Fisher)

Hypothèse statistique ● Un résultat non statistiquement significatif peut avoir 2 causes : – – l’hypothèse H 0 est vraie (i. e. il y a équivalence entre les deux groupes) la puissance statistique n’est pas suffisante (i. e. nombre de sujets insuffisant)

III Inférence statistique en étudiant plusieurs paramètres

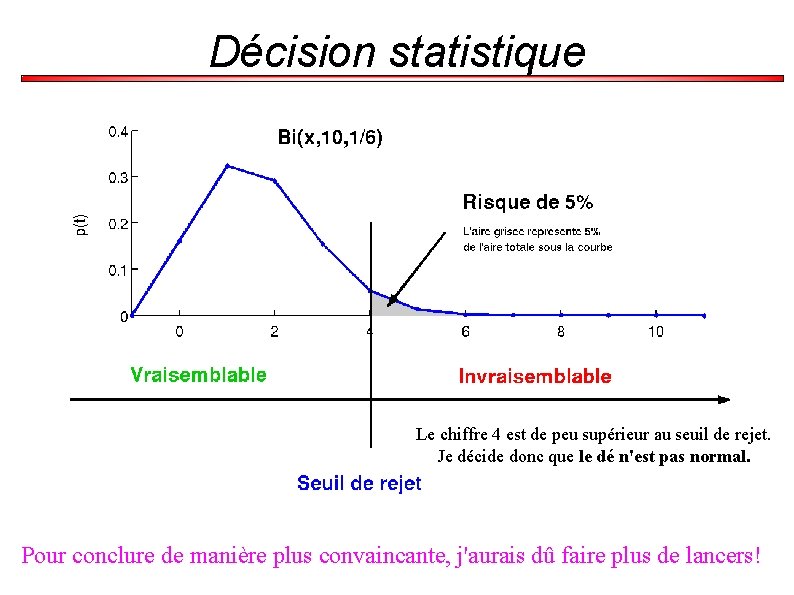
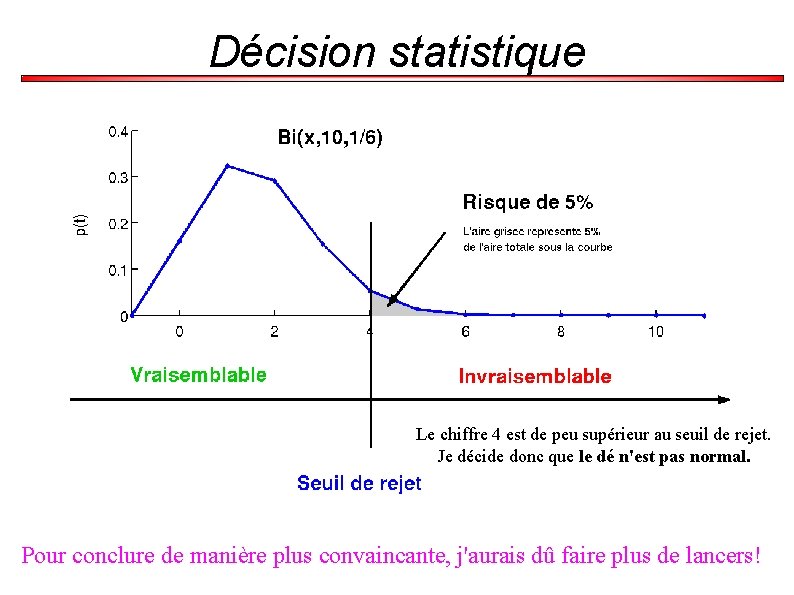
Décision statistique Le chiffre 4 est de peu supérieur au seuil de rejet. Je décide donc que le dé n'est pas normal. Pour conclure de manière plus convaincante, j'aurais dû faire plus de lancers!

Étapes d'un test d'hypothèse (1) Formuler ses hypothèses Poser H 0 et H 1 (2) Choix du test approprié Le cours est là pour vous présenter les tests (3) Spécifier un niveau de signification (� ) et la taille de l'échantillon (N) (4) Trouver la distribution d'échantillonnage du test statistique (5) Calculer la région de rejet (6) Tirer une conclusion Si la probabilité est très faible, on rejette l'hypothèse

Hypothèse statistique ● Puissance statistique : (1 - – – – c’est l’aptitude à mettre en évidence une différence lorsqu’elle existe cf Test diagnostic : sensibilité on calcule un nombre de sujets nécessaire pour obtenir une puissance donnée

Hypothèse statistique 6. Le degré de signification ( « p » ) Ex : si les taux de succès sous corticoïdes et sous placebo sont identiques, la probabilité d’observer une telle différence (i. e. 51, 2% vs 23, 8%) ou une différence plus grande encore est de 0, 009

Hypothèse statistique ● Définition : – – quantifie le « désaccord » entre ce qu’on observe et l’hypothèse nulle H 0 la probabilité d’observer des résultats au moins aussi en désaccord avec l’hypothèse nulle H 0 que ceux qu’on a observés

Retour sur les expériences de Mendel a étudié différentes plantes pouvant s'hybrider facilement. Ses expériences confirment-elles la théorie de l'hybridation ?

Retour sur les expériences de Mendel (Mendel, 1865) a mis en évidence les mécanismes de l'hérédité Certains caractères sont dominants (A), d'autres récessifs (a). À la génération F 2, on attend donc à avoir ¾ des échantillons présentant le caractère A. 0. 012=1. 2%

Retour sur les expériences de Mendel Ses expériences confirment-elles la théorie de l'hybridation ?

Hypothèse statistique ● Interprétation : – plus le degré de signification est faible, plus on est convaincu que les résultats observés ne sont pas en cohérence avec l’hypothèse nulle

Hypothèse statistique ATTENTION !!!! (1) Le degré de signification nous permet d’affirmer avec plus ou moins de conviction qu’il y a une différence, mais en aucun cas il ne nous renseigne sur l’importance de cette différence

Hypothèse statistique ● Exemple : – – – 1) 22/43 (51, 2%) vs 10/42 (23, 8%) Différence d’efficacité = 27, 4% (p = 0, 009) 2) 14/22 (63, 6%) vs 5/21 (23, 8%) Différence d’efficacité = 39, 8% (p = 0, 009) 3) 1104/4200 (26, 3%) vs 1000/4200 (23, 8%) Différence d’efficacité = 2, 5% (p = 0, 009)

Test d'hypothèse = détermination de la plausibilité qu'un paramètre d'un modèle prenne des valeurs différentes dans des populations distinctes, afin de mettre en évidence, ou non, un effet d'un facteur expérimental sur une population.

Hypothèse statistique ● La valeur de p dépend : – – ● de la différence observée entre les deux groupes de la taille d’échantillon S’il existe une différence réelle, aussi infime soit-elle, entre 2 groupes, n’importe quel test statistique va aboutir à une valeur de p inférieure à 0, 05, dès lors que le nombre de sujets étudiés sera important

Hypothèse statistique La signification statistique n’implique pas la pertinence clinique

Courbe de puissance d'un test statistique Souvent on ne connaît pas la loi de probabilité de H 1 car il nous manque un seul paramètre. Dans le cas du dé, ce serait de connaître la probabilité de tirer un 1 Courbe de puissance (d'un test statistique) = Courbe caractéristique d'efficacité = Fonction donnant 1 -� pour chaque valeur du paramètre inconnu de H 1, pour �donné.

Hypothèse statistique ATTENTION !!!! (2) Ne pas mettre en évidence de différence statistiquement significative entre deux groupes ne signifie pas qu’il y ait équivalence entre les deux groupes

Hypothèse statistique ● Ex : 0/3 (0, 0%) vs 3/3 (100, 0%) Différence d’efficacité = 100, 0% p = 0, 010 (test exact de Fisher)

Hypothèse statistique ● Un résultat non statistiquement significatif peut avoir 2 causes : – – l’hypothèse H 0 est vraie (i. e. il y a équivalence entre les deux groupes) la puissance statistique n’est pas suffisante (i. e. nombre de sujets insuffisant)

Sources de variabilité Imprécision ≠ Inexactitude Si la mesure effective diffère de la valeur réelle, on parle alors d'inexactitude. Elle souvent due à une erreur dans le protocole expérimental. Elle est aussi introduite lorsqu'on étudie un échantillon peu représentatif de la population. Attention : l'inexactitude peut être masquée

Sources de variabilité (2) Différences individuelles Les éléments de l'échantillon sont différents.

Sources de variabilité (3) Différences factorielles Les éléments placés dans un environnement différent ont des propriétés différentes. On cherche souvent à caractériser de telles différences.

Sources de variabilité Variabilité résiduelle = imprécision + variabilité individuelle Variabilité totale = variabilité résiduelle + variabilité factorielle

Bruit Information Sources de variabilité Population Variabilité factorielle Variabilité individuelle Incertitude Facteur = a El 1 El 2 El 3 Facteur = b Facteur = c

Repérer les sources de variabilité (1) Imprécision : faire la mesure 2 fois, dans les mêmes conditions, sur le même élément. (2) Variabilité individuelle : faire la mesure dans les mêmes conditions, sur au moins 2 éléments. (3) Variabilité factorielle : faire la mesure dans les mêmes conditions, sur au moins 2 éléments sur 2 niveaux de ce facteur.

Réduire les sources de variabilité (1) Imprécision : Améliorer la technique de mesure (2) Variabilité individuelle : Standardiser l'expérience en ne mélangeant pas différentes groupes dans l'étude. Bien définir la population (3) Variabilité factorielle : Irréductible. La variabilité factorielle est souvent ce que l'on veut mettre en évidence.

Modélisation On identifie la variabilité factorielle sous-groupe i individu i, j de ce sous groupe X=� +a + e

Paradoxe des statistiques Une étude cherche à tester une hypothèse On pourra : - éventuellement prouver la validité de l'hypothèse - mais jamais l'infirmer ! Il faut donc choisir la bonne hypothèse

Unilatéral ou bilatéral ? Il y a beaucoup de façons de contredire H 0, ce qu'on retrouve dans le choix de la latéralité du test, ce qui se retrouve dans la formulation de H 1, Le test bilatéral si l'hypothèse H 1 est symétrique. Ex : « dé pipé » Le test latéral si l'hypothèse H 1 est dissymétrique. Ex : « dé pipé vers les petites valeurs »

Décision statistique Le chiffre 4 est de peu supérieur au seuil de rejet. Je décide donc que le dé n'est pas normal. Pour conclure de manière plus convaincante, j'aurais dû faire plus de lancers!

Modélisation On identifie la variabilité factorielle sous-groupe i individu i, j de ce sous groupe X=� +a + e

Paradoxe des statistiques Une étude cherche à tester une hypothèse On pourra : - éventuellement prouver la validité de l'hypothèse - mais jamais l'infirmer ! Il faut donc choisir la bonne hypothèse